做 AB 实验时,业务方(PM/运营)和数据科学家(DS)之间永远存在一场拉锯战:
- 业务方:"我想省点流量,能不能只切 1% 的用户跑实验?万一搞砸了影响面也小。"
- 数据科学家:"不行,流量太少测不准,起码要 10%。"
- 业务方:"那到底最少要多少人?给个数。"
这个问题看似简单,实则触及了 AB 实验的成本核心。样本量不是拍脑袋定的,它是由你想要多大的"确定性"和多精细的"分辨率"决定的。
今天我们来拆解这个决定实验生死的计算过程:最小样本量 (Minimum Sample Size) 的计算。
1. 灵魂拷问:为什么不能想跑多少就跑多少?
在回答"怎么算"之前,先回答"为什么算"。
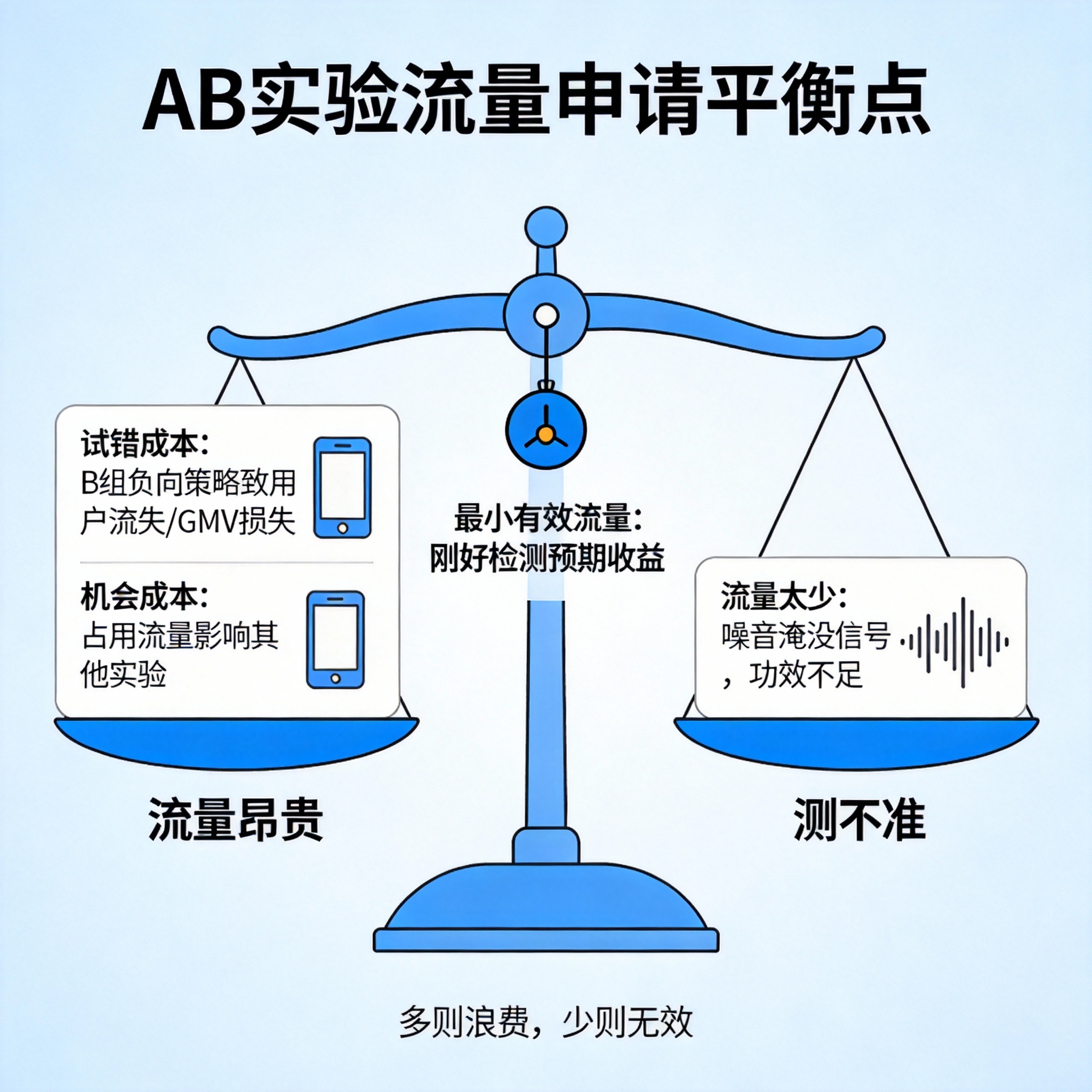
我们不能无限堆流量,因为流量昂贵。
- 试错成本:如果 B 组策略是负向的(比如导致 App 崩溃,或者新 UI 丑到用户卸载),样本量越大,得罪的用户越多,损失的 GMV 越大。
- 机会成本:流量是有限资源。你占用了 50% 的流量跑这个颜色测试,别的更重要的算法排序实验就没流量跑了。
另一方面,我们也不能只跑一点点流量。
- 测不准 :流量太少,噪音(方差)太大,真实收益(信号)会被淹没。这会导致功效 (Power) 不足,明明策略有效,你却检测不出来,错失良机。
所以,我们需要找到一个平衡点 :刚好 能检测出预期收益的最小流量。多一个浪费,少一个不行。
2. 核心公式:参数铁三角
计算样本量的公式看起来很吓人,但我们把它拆解开,其实就是三个力量的博弈。
对于双样本均值检验(比如对比 A/B 两组的人均 GMV),每组所需的样本量 NNN 的近似公式为:
N≈2σ2(Z1−α/2+Z1−β)2δ2 N \approx \frac{2 \sigma^2 (Z_{1-\alpha/2} + Z_{1-\beta})^2}{\delta^2} N≈δ22σ2(Z1−α/2+Z1−β)2
让我们逐一拆解这个公式里的每一个因子,看看它们是如何左右样本量的。
2.1 分子第一项:噪音 σ2\sigma^2σ2 (Variance)
- 含义:数据的波动程度(方差)。
- 逻辑 :σ2\sigma^2σ2 在分子上。
- 数据波动越大(噪音越大),你需要的样本量 NNN 就越大。
- 实战启示 :这就是为什么我们在前几篇拼命讲 CUPED 和分层抽样------降低 σ2\sigma^2σ2 是减少样本量最直接、最"免费"的手段。 如果你能通过算法把方差降一半,样本量就能省一半。
2.2 分子第二项:置信度与功效 (Z1−α/2+Z1−β)2(Z_{1-\alpha/2} + Z_{1-\beta})^2(Z1−α/2+Z1−β)2
这是我们对"准确性"的要求,也就是我们给自己设定的"判罚红线"。
- Z1−α/2Z_{1-\alpha/2}Z1−α/2 :对应显著性水平 α\alphaα (通常取 0.05,对应 Z 值约 1.96)。
- 代表我们要控制**误报(假阳性)**的概率。
- Z1−βZ_{1-\beta}Z1−β :对应统计功效 1−β1-\beta1−β (通常取 80%,对应 Z 值约 0.84)。
- 代表我们要控制**漏报(假阴性)**的概率。
- 逻辑 :这两个值也在分子上。
- 你想越有把握(α\alphaα 越低,Power 越高),你付出的样本量代价就越大。如果你想要 99% 的功效,样本量可能要翻倍。
2.3 分母:MDE δ\deltaδ (Minimum Detectable Effect)
- 含义 :最小可检测效应。这是全篇最核心的概念。
- 逻辑 :δ\deltaδ 在分母上,而且是平方 。
- 这意味着:如果你想检测的提升幅度越小(δ\deltaδ 越小),样本量 NNN 就会指数级爆炸。
- 想检测 1% 的提升 vs 想检测 0.1% 的提升,后者需要的样本量是前者的 100 倍,而不是 10 倍。
3. 深度解析:MDE------显微镜的哲学
很多新人最难理解的就是 MDE。我们用**"显微镜"**来类比。
AB 实验就是用显微镜找细菌。
- MDE (δ\deltaδ) = 你要观察的目标物体的大小。
- 样本量 (NNN) = 显微镜镜片的厚度(放大倍数)。
场景 A:观察大象(大提升)
- 目标 :你上线了一个颠覆性改版(比如把收费变成免费),你预期它能带来 10% 的惊人增长(δ\deltaδ 很大)。
- 策略:既然目标这么大,你肉眼都能看见,根本不需要显微镜。
- 代价 :样本量只需要很少就能看清。
场景 B:观察细菌(微小提升)
- 目标 :你优化了一个按钮的圆角,或者改了一个文案的标点,预期只能带来 0.1% 的微弱增长(δ\deltaδ 很小)。
- 策略:为了看清这么小的东西,你需要一个放大倍数极高的显微镜。
- 代价 :你需要堆叠极厚的镜片。样本量需要极大 。
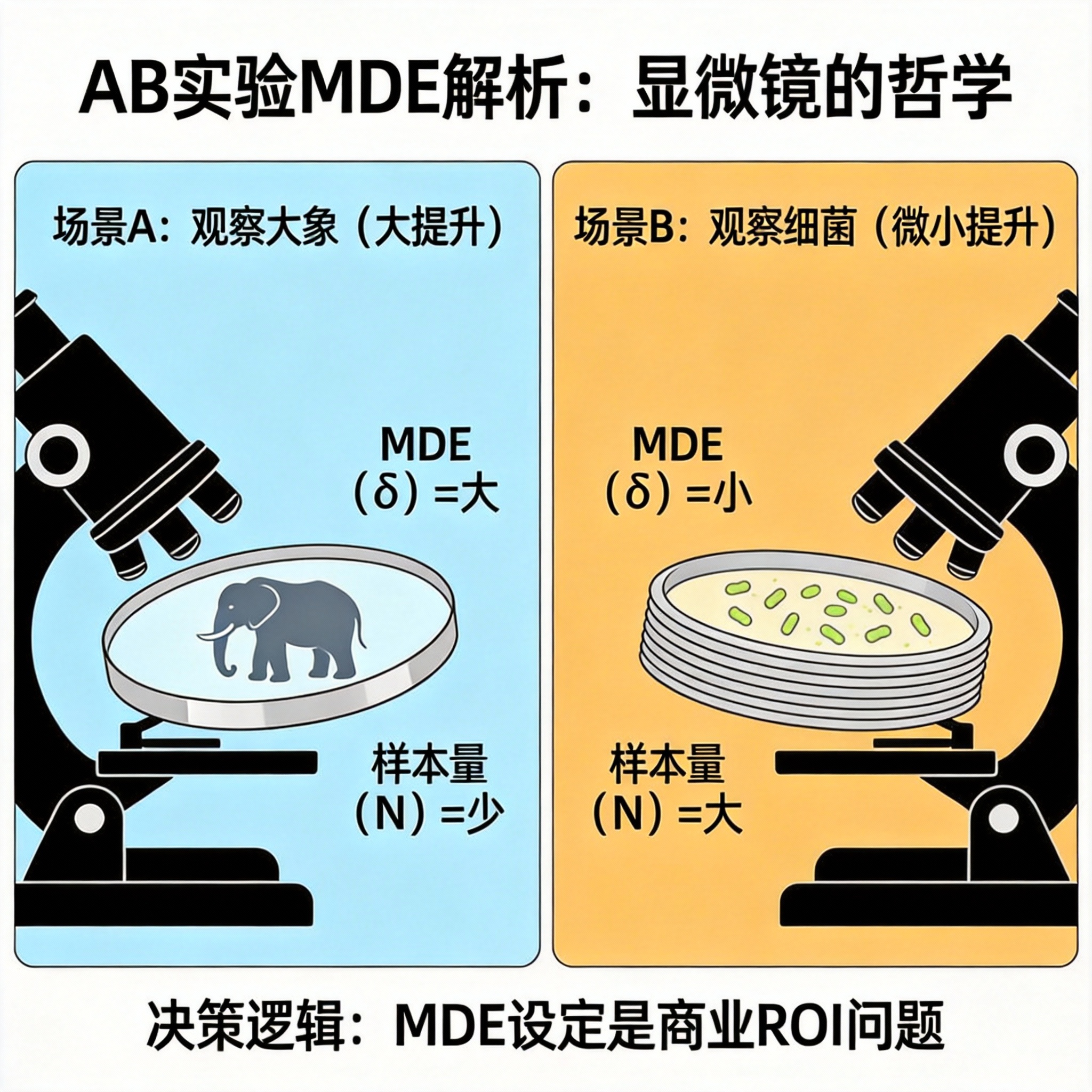
决策逻辑 :
设定 MDE 不是统计学问题,而是商业 ROI 问题 。
你应该问业务方:"多大的提升对我们来说是有意义的?" - 如果提升 0.1% 带来的营收还覆盖不了开发成本,那我们根本不需要去观察 0.1% 的细菌。
- 把 MDE 设为 1%(只看大虫子),这样样本量能省下 99%。如果实验不显著,说明提升没到 1%,那就算有提升(比如 0.5%)我们也不在乎,直接放弃即可。
没问题,我们继续拆解剩下的核心误区与实战心法。
4. 易混淆概念:MDE vs Δ\DeltaΔ (Delta)
这是实战中最大的乌龙来源,也是无数数据分析师被业务方"冤枉"的重灾区。
为了搞清楚它俩的区别,我们继续沿用**"显微镜"**的类比:
-
MDE (Minimum Detectable Effect):
- 时间点 :实验开始前设定。
- 属性 :这是你的预期 ,是你这台显微镜的分辨率上限。
- 人话 :"我这台显微镜,最小能看清 1微米 的细菌。比这个再小的,我就看不清了(不显著)。"
-
Δ\DeltaΔ (Actual Difference / Delta):
- 时间点 :实验结束后计算。
- 属性 :这是客观事实 ,是策略带来的真实变化值(μtreatment−μcontrol\mu_{treatment} - \mu_{control}μtreatment−μcontrol)。
- 人话 :"这个细菌实际的大小是 0.5微米。"
惨案现场:为什么涨了却不显著?
场景还原:
- 实验前:你跟业务方商量,设定 MDE = 1%(即我们需要 1% 的提升才能回本)。根据这个 MDE,你算出需要 10 万样本量。
- 实验后 :数据跑出来了,实验组比对照组确实涨了,真实差异 Δ\DeltaΔ = 0.5%。
- 结果:P 值 > 0.05(不显著)。
业务方炸毛:"明明涨了 0.5%,凭什么说不显著?是不是你算的 P 值有问题?"
你的回答 :
"不是 P 值有问题,是显微镜倍数不够 。
我们当初约定的是'只抓 1% 的大鱼'(MDE=1%),所以只准备了 10 万样本(低倍镜)。
现在来了一条 0.5% 的小鱼(Δ\DeltaΔ = 0.5%),虽然它确实存在,但在 10 万样本的低倍镜下,它看起来和'杂质'(噪音)没区别。
如果当初你想抓 0.5% 的鱼,我们就应该准备 40 万样本(高倍镜)。"
结论 :当 Δ<MDE\Delta < \text{MDE}Δ<MDE 时,实验大概率是不显著的。这不是数学错误,这是资源错配。
5. 警惕伪科学:Post-hoc Power (事后功效)
在实验不显著(P > 0.05)时,经常有"懂一点统计学"的业务方会提要求:
"是不是因为 Power 不够?我们要不要算一下现在的 Power 是多少?如果 Power 低,是不是说明其实有效但没测出来?"
请直接拒绝这种要求。
事后功效分析 (Post-hoc Power Analysis) 是统计学界的伪科学。
为什么它是错的?
Power 的定义是:"在假设真实效应存在的前提下,我们能检测出它的概率。"
当你实验跑完,数据已经成了定局。此时:
- 如果 P > 0.05(不显著),由数学公式可直接推导,算出来的 Observed Power 一定很低。
- 这就像足球比赛已经结束了,你输了 0:1。这时候你再去算"我这场比赛赢的概率是多少",算出来肯定是 0。这能说明什么?说明你运气不好?不,这毫无意义,因为结果已经发生了。
正确做法
Power 和样本量计算,必须且只能在实验开始前 (Pre-experiment) 完成。
如果跑完不显著,你只有两条路:
- 认栽 :承认策略效果没达到预期(Δ<MDE\Delta < \text{MDE}Δ<MDE),放弃策略。
- 加注 :如果你坚信策略有效,只是 Δ\DeltaΔ 比预想的小(比如原以为涨 1%,实际只涨了 0.5%),那么请重新设定一个更小的 MDE ,计算出更大的样本量,然后追加流量重跑(或者延长实验时间)。
总结
回顾这一章,我们其实只讲了一件事:不要打无准备之仗。
- 样本量是算出来的,不是拍出来的 :它取决于你对风险的容忍度 (α,β\alpha, \betaα,β) 和对收益的渴望程度 (δ\deltaδ)。
- MDE 是核心博弈点 :
- 想测得越细(MDE 越小),样本量代价越大(平方级爆炸)。
- 不要盲目追求低 MDE,要结合业务 ROI 设定。如果 0.1% 的提升不值钱,就别为了它浪费宝贵的流量。
- 决胜于未战 :所有的参数设定(α,β,MDE\alpha, \beta, \text{MDE}α,β,MDE)必须在实验开始前完成。一旦实验开始,请尊重数据,不要试图从事后分析(Post-hoc)中寻找安慰。
如果这篇文章帮你理清了思路,不妨点个关注。我会持续分享 AB 实验、因果推断的硬核实战笔记,拒绝水文,只讲干货。
