LeetCode 1895.最大的幻方：暴力中来点前缀和优化

【LetMeFly】1895.最大的幻方：暴力中来点前缀和优化

力扣题目链接：https://leetcode.cn/problems/largest-magic-square/

一个 k x k 的幻方指的是一个 k x k 填满整数的方格阵，且每一行、每一列以及两条对角线的和全部相等。幻方中的整数 不需要互不相同 。显然，每个 1 x 1 的方格都是一个幻方。

给你一个 m x n 的整数矩阵 grid ，请你返回矩阵中 最大幻方 的尺寸（即边长 k）。

示例 1：

复制代码

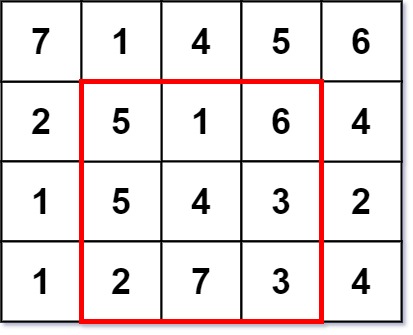
输入：grid = [[7,1,4,5,6],[2,5,1,6,4],[1,5,4,3,2],[1,2,7,3,4]]
输出：3
解释：最大幻方尺寸为 3 。
每一行，每一列以及两条对角线的和都等于 12 。
- 每一行的和：5+1+6 = 5+4+3 = 2+7+3 = 12
- 每一列的和：5+5+2 = 1+4+7 = 6+3+3 = 12
- 对角线的和：5+4+3 = 6+4+2 = 12

示例 2：

复制代码

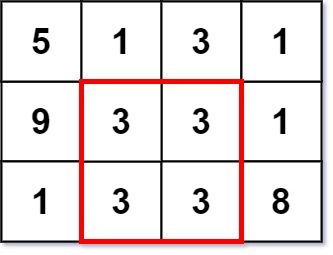
输入：grid = [[5,1,3,1],[9,3,3,1],[1,3,3,8]]
输出：2

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
1 <= grid[i][j] <= 10⁶

解题方法：暴力中来点前缀和优化

最为暴力的做法是什么？

枚举边长 k k k（可从大到小枚举），复杂度 O ( min ⁡ ( m , n ) ) O(\min(m, n)) O(min(m,n))
枚举幻方左上角，复杂度 O ( m n ) O(mn) O(mn)
对于一个方块，判断其是否为幻方，复杂度 O ( k 2 ) O(k^2) O(k2)

总计复杂度 O ( n 5 ) O(n^5) O(n5)，而 50 5 = 312 , 500 , 000 = 3.12 e 8 50^5=312,500,000=3.12e8 505=312,500,000=3.12e8会超时，所以需要想办法优化一层循环。

不难发现，我们在判断一个方块是否为幻方时要暴力计算每一行之和，而一行的元素和使用前缀和即可 O ( 1 ) O(1) O(1)算出，所以我们可以预处理计算出一个横向上的前缀和以及一个纵向上的前缀和（斜向由于只有两条所以无需前缀和加速）。

这样，时间复杂度就降低为了 O ( n 4 ) O(n^4) O(n4)，而 50 4 = 6 , 250 , 000 = 6.25 e 6 50^4=6,250,000=6.25e6 504=6,250,000=6.25e6可以接受。

时间复杂度 O ( m n ⋅ min ⁡ ( m , n ) ) O(mn\cdot\min(m,n)) O(mn⋅min(m,n))
空间复杂度 O ( m n ) O(mn) O(mn)

AC代码

C++

cpp 复制代码

/*
 * @LastEditTime: 2026-01-18 23:17:50
 */
class Solution {
private:
    vector<vector<int>> rowSum, colSum;

    bool ok(vector<vector<int>>& grid, int x, int y, int l) {
        int cnt = 0, cntRev = 0;
        for (int i = 0; i < l; i++) {
            cnt += grid[x + i][y + i];
            cntRev += grid[x + i][y + l - i - 1];  // 易错
        }
        if (cnt != cntRev) {
            return false;
        }
        for (int i = 0; i < l; i++) {
            if (rowSum[x + i][y + l] - rowSum[x + i][y] != cnt) {
                return false;
            }
            if (colSum[x + l][y + i] - colSum[x][y + i] != cnt) {
                return false;
            }
        }
        return true;
    }
public:
    int largestMagicSquare(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        rowSum.resize(n, vector<int>(m + 1));
        colSum.resize(n + 1, vector<int>(m));

        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                rowSum[i][j + 1] = rowSum[i][j] + grid[i][j];
                colSum[i + 1][j] = colSum[i][j] + grid[i][j];
            }
        }

        for (int k = n; k > 1; k--) {
            for (int i = 0; i + k <= n; i++) {
                for (int j = 0; j + k <= m; j++) {
                    if (ok(grid, i, j, k)) {
                        return k;
                    }
                }
            }
        }
        return 1;
    }
};

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源