本专栏以每天一至两篇的速度更新,关注我 ,及时更新你的 AI 提示词库。
经济订货量(EOQ)扩展模型:有限生产率场景下的库存优化
1. 摘要
在传统EOQ模型中,"瞬时补货"假设(即订单下达后整批货物立即入库)是核心前提之一,但在制造业等场景中,企业通常通过自有生产线生产补货,生产过程以有限速率持续进行(而非瞬时完成)。有限生产率EOQ模型通过放松"瞬时补货"假设,整合生产速率与需求速率的动态关系,构建更贴合实际生产场景的库存决策工具。本文基于统一符号体系,结合库存动态图(图1),系统阐述该模型的核心逻辑、公式推导与应用价值。
2. 模型核心假设与参数定义
2.1. 核心假设
有限生产率EOQ模型延续传统EOQ的基础假设,仅调整补货方式相关设定:
- 需求率( μ \mu μ)恒定且已知,单位为"件/单位时间";
- 订货成本( K K K)为单次生产准备的固定成本(与生产批量无关);
- 持有成本率( h h h)为单位产品持有单位时间的成本,恒定不变;
- 生产速率( λ \lambda λ)恒定且已知,满足 λ > μ \lambda > \mu λ>μ(生产速率需高于需求速率,否则无法持续满足需求);
- 生产启动后,产品以速率 λ \lambda λ持续入库,无缺货、无生产中断,库存管理为多周期场景。
2.2. 参数定义(与基础EOQ模型保持一致)
- λ \lambda λ:生产速率(件/单位时间),即生产线单位时间的产出量;
- μ \mu μ:需求率(件/单位时间),即单位时间内的产品消耗量;
- Q Q Q:生产批量(件),即每次生产的产品数量;
- K K K:生产准备成本(货币单位/次),即每次启动生产线的固定成本;
- h h h:持有成本率(货币单位/(件·单位时间));
- Π ( Q ) \Pi(Q) Π(Q):单位时间总库存成本(货币单位/单位时间)。
3. 库存动态与关键参数推导(结合图1)
图1展示了有限生产率场景下的库存动态变化(横轴为时间,纵轴为库存水平),其核心过程分为"生产阶段"与"消耗阶段",各阶段的关键参数推导如下:
3.1. 图1:有限生产率下的库存动态图
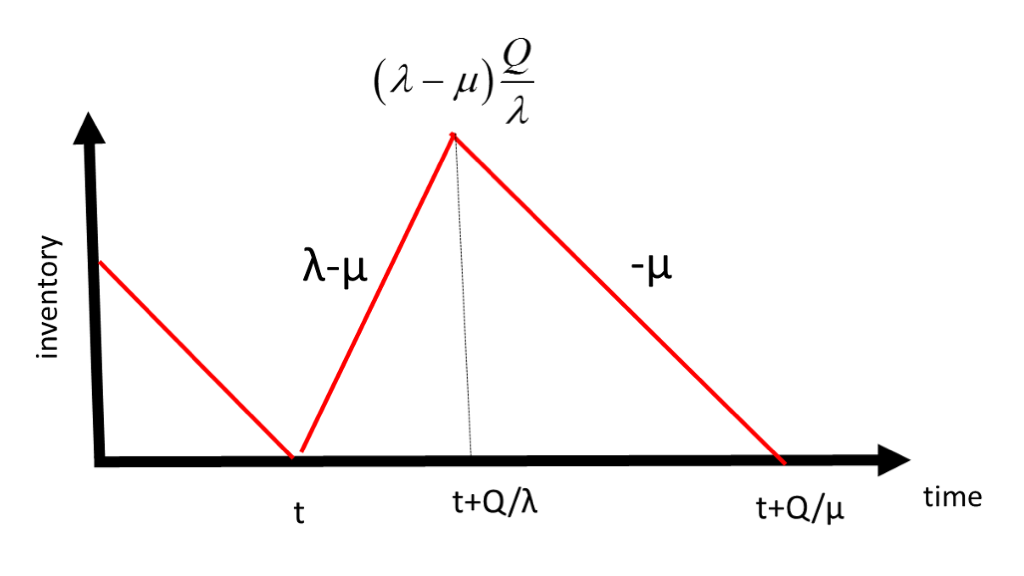
(注:图中红色曲线为库存水平变化, t t t为生产启动时刻, t + Q / λ t+Q/\lambda t+Q/λ为生产结束时刻, t + Q / μ t+Q/\mu t+Q/μ为库存耗尽时刻)
3.2. 生产阶段( t → t + Q / λ t \to t+Q/\lambda t→t+Q/λ)
在时刻 t t t,库存水平降至0(或安全库存),启动生产:
- 生产持续时间:生产批量为 Q Q Q,生产速率为 λ \lambda λ,因此生产阶段时长为 Q λ \frac{Q}{\lambda} λQ;
- 库存净积累速率:生产过程中,产品以速率 λ \lambda λ入库,同时以速率 μ \mu μ消耗,因此库存净积累速率为 λ − μ \lambda - \mu λ−μ;
- 最大库存水平:生产结束时( t + Q / λ t+Q/\lambda t+Q/λ),库存达到最大值,即净积累速率乘以生产时长:
I max = ( λ − μ ) ⋅ Q λ I_{\text{max}} = (\lambda - \mu) \cdot \frac{Q}{\lambda} Imax=(λ−μ)⋅λQ
3.3. 消耗阶段( t + Q / λ → t + Q / μ t+Q/\lambda \to t+Q/\mu t+Q/λ→t+Q/μ)
生产结束后,生产线停止运行,库存仅以需求率 μ \mu μ消耗:
- 消耗阶段时长:库存从最大值 I max I_{\text{max}} Imax耗尽所需时间,即 I max μ \frac{I_{\text{max}}}{\mu} μImax,代入 I max I_{\text{max}} Imax的表达式后化简为:
Q μ − Q λ \frac{Q}{\mu} - \frac{Q}{\lambda} μQ−λQ - 生产-消耗周期:完整的"生产-消耗"周期时长为生产阶段与消耗阶段之和,即 Q μ \frac{Q}{\mu} μQ,与传统EOQ模型的订货间隔一致。
3.4. 平均库存水平
与传统EOQ模型类似,有限生产率场景下的库存水平在"0-最大库存"之间线性变化(生产阶段上升、消耗阶段下降),因此平均库存水平 为最大库存的一半:
I avg = I max 2 = ( λ − μ ) Q 2 λ I_{\text{avg}} = \frac{I_{\text{max}}}{2} = \frac{(\lambda - \mu)Q}{2\lambda} Iavg=2Imax=2λ(λ−μ)Q
4. 总成本函数与最优生产批量推导
4.1. 总成本函数构建
总库存成本仍由生产准备成本、持有成本与生产变动成本(对应传统EOQ的采购成本)三部分构成,其中:
- 生产变动成本:单位生产变动成本为 c c c,单位时间生产变动成本为 c μ c\mu cμ(与生产批量无关);
- 生产准备成本:单位时间内的生产准备次数为 μ Q \frac{\mu}{Q} Qμ,因此单位时间生产准备成本为 K μ Q \frac{K\mu}{Q} QKμ;
- 持有成本:单位时间持有成本为 h ⋅ I avg h \cdot I_{\text{avg}} h⋅Iavg,代入平均库存表达式后为 h ⋅ ( λ − μ ) Q 2 λ h \cdot \frac{(\lambda - \mu)Q}{2\lambda} h⋅2λ(λ−μ)Q。
综上,单位时间总库存成本函数为:
Π ( Q ) = c μ + K μ Q + h ⋅ ( λ − μ ) Q 2 λ \Pi(Q) = c\mu + \frac{K\mu}{Q} + h \cdot \frac{(\lambda - \mu)Q}{2\lambda} Π(Q)=cμ+QKμ+h⋅2λ(λ−μ)Q
4.2. 最优生产批量( Q ∗ Q^* Q∗)推导
为简化公式,定义调整后持有成本率 h ^ \hat{h} h^(即考虑有限生产率后的有效持有成本):
h ^ = h ⋅ λ − μ λ \hat{h} = h \cdot \frac{\lambda - \mu}{\lambda} h^=h⋅λλ−μ
此时总成本函数可改写为与传统EOQ模型一致的形式:
Π ( Q ) = c μ + K μ Q + h ^ Q 2 \Pi(Q) = c\mu + \frac{K\mu}{Q} + \frac{\hat{h}Q}{2} Π(Q)=cμ+QKμ+2h^Q
对该函数关于 Q Q Q求导并令导数为0,即可得到最优生产批量:
Q ∗ = 2 K μ h ^ = 2 K μ λ h ( λ − μ ) Q^* = \sqrt{\frac{2K\mu}{\hat{h}}} = \sqrt{\frac{2K\mu\lambda}{h(\lambda - \mu)}} Q∗=h^2Kμ =h(λ−μ)2Kμλ
4.3. 最小总库存成本
将最优生产批量 Q ∗ Q^* Q∗代入总成本函数,可得到单位时间最小总库存成本:
Π ( Q ∗ ) = c μ + 2 K μ h ( λ − μ ) λ \Pi(Q^*) = c\mu + \sqrt{\frac{2K\mu h(\lambda - \mu)}{\lambda}} Π(Q∗)=cμ+λ2Kμh(λ−μ)
5. 实例演算
假设某制造企业的生产-库存系统参数如下:
- 生产速率 λ = 250 \lambda = 250 λ=250件/年;
- 需求率 μ = 100 \mu = 100 μ=100件/年;
- 生产准备成本 K = 75 K = 75 K=75货币单位/次;
- 持有成本率 h = 10 h = 10 h=10货币单位/(件·年);
- 单位生产变动成本 c = 50 c = 50 c=50货币单位/件。
5.1. 计算调整后持有成本率
h ^ = 10 ⋅ 25 − 100 250 = 6 货币单位/(件-年) \hat{h} = 10 \cdotp \frac{25-100}{250}=6 \ \text{货币单位/(件-年)} h^=10⋅25025−100=6 货币单位/(件-年)
5.2. 计算最优生产批量
Q ∗ = 2 × 75 × 100 6 = 2500 = 50 件 Q^* = \sqrt{\frac{2 \times 75 \times 100}{6}} = \sqrt{2500} = 50 \text{件} Q∗=62×75×100 =2500 =50件
5.3. 计算最小总库存成本
Π ( Q ∗ ) = 50 × 100 + 2 × 75 × 100 × 10 × ( 250 − 100 ) 250 = 5000 + 300 = 5300 货币单位/年 \Pi(Q^*) = 50 \times 100 + \sqrt{\frac{2 \times 75 \times 100 \times 10 \times (250 - 100)}{250}} = 5000 + 300 = 5300 \text{货币单位/年} Π(Q∗)=50×100+2502×75×100×10×(250−100) =5000+300=5300货币单位/年
6. 模型核心特性与应用价值
6.1. 核心特性
- 生产速率的影响:生产速率 λ \lambda λ越大,调整后持有成本率 h ^ \hat{h} h^越接近 h h h,最优生产批量 Q ∗ Q^* Q∗越接近传统EOQ(当 λ → ∞ \lambda \to \infty λ→∞时, Q ∗ Q^* Q∗与传统EOQ完全一致);
- 库存水平的降低:由于生产过程持续进行,平均库存水平( ( λ − μ ) Q 2 λ \frac{(\lambda - \mu)Q}{2\lambda} 2λ(λ−μ)Q)低于传统EOQ的 Q 2 \frac{Q}{2} 2Q,可减少仓储空间占用与资金占用。
6.2. 应用价值
- 贴合制造业生产场景:适用于自有生产线生产补货的企业,如电子元件制造、食品加工等行业;
- 平衡生产与库存成本:通过量化生产速率与需求速率的关系,避免"过度生产导致库存积压"或"生产不足导致需求缺失"的问题;
- 与精益生产的协同:有限生产率模型的核心逻辑与"小批量、多批次"的精益生产理念一致,可通过提高生产速率( λ \lambda λ)或降低生产准备成本( K K K),进一步减小生产批量,实现"准时化生产"。
有限生产率EOQ模型通过整合生产过程的动态特性,弥补了传统EOQ模型"瞬时补货"假设的局限性,为制造业企业提供了更精准的库存-生产联合决策工具。其核心逻辑在于"平衡生产准备成本与库存持有成本",同时考虑生产速率对库存积累的影响,最终实现生产与库存的协同优化。