9种常用排序算法总结

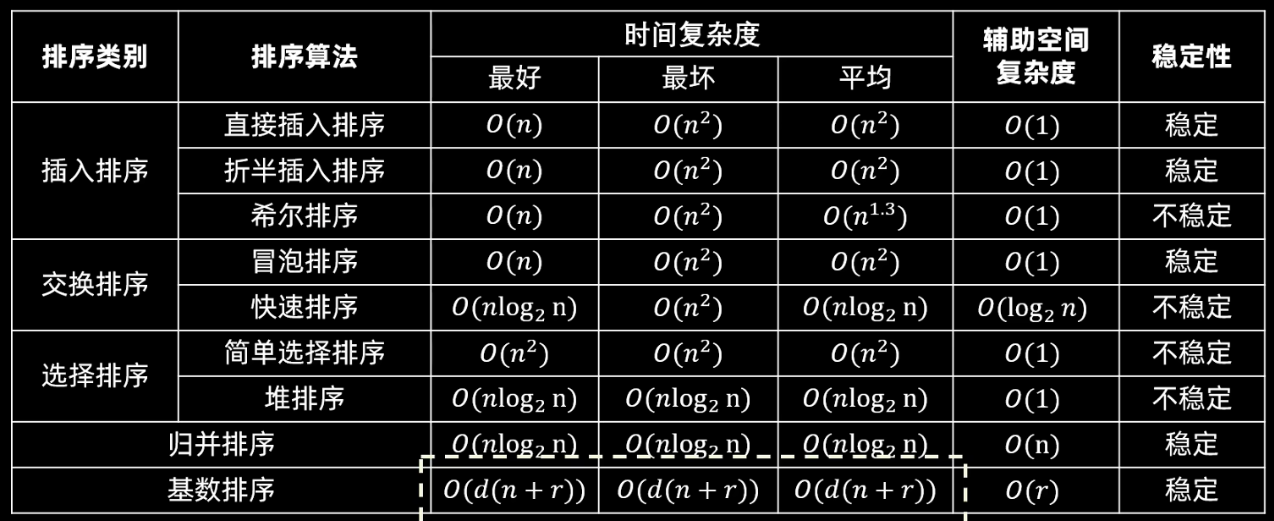
一、插入排序

基本思想：每一趟将一个待排序的记录，按其关键字的大小插入到已经排序好的一组记录的适当位置上，直到全部待排序记录全部插入为止。

1.1 直接插入排序

排序过程：

将待排序数组arr[1...n]看作两个集合，arr[1]为有序集合中元素，arr[2...n]为无序集合中元素，a[0]用来临时存放当前待排序记录
外层循环每次从无序集合中选择一个待插入元素（n-1次），每次使用顺序查找法，内层循环查找arr[i]在有序集合中的位置（将有序集合中大于待插入元素的记录后移一位）

java 复制代码

public class InsertionSort{
    //直接插入排序方法
    public static void insertionSort(int[] arr){
        if (arr == null || arr.length<=1){
            return;
        }
        //从第二个元素开始（第一个元素默认已排序）
        for (int i=1;i<arr.length;i++){
            int key=arr[i];
            int j=i-1;

            // 将比key大的元素向后移动
            while(j>=0 && arr[j] > key){
                arr[j+1]=arr[j];
                j--;
            }
            // 插入key到正确位置
            arr[j+1] = key;
        }
    }
}

时间复杂度：

最好情况下（待排序记录递增有序），总的比较次数为n-1次，记录不需要移动。
最坏情况下（待排序记录递减有序），总的比较次数和移动次数均为n^2/2。
平均情况下，比较次数和移动次数都是n^2/4。

空间复杂度：

只需要一个辅助空间arr[0],因此空间复杂度为O(1)

1.2 折半插入排序

基本思想同直接查找插入排序，不同点在于，在有序集合中搜索插入位置时折半插入采用二分搜索，可以有效的减少比较次数。

java 复制代码

public static void binaryInsertionSortDetailed(int[] arr){
    if(arr == null || arr.length <=1){
        return;
    }
    
    for(int i=1; i<arr.length;i++){
    int key = arr[i]; //待插入的元素
    
    //使用二分查找在已排序部分[0,i-1]中找到插入位置
    int insertPos = binarySearch(arr,0,i-1,key);

    //将元素后移，为插入腾出空间
    for(int j=i-1;j>insertPos;j--){
       arr[j=1]=arr[j]; 
       }
    //插入元素
    arr[insertPos]=key;
    }
}

时间复杂度：

该算法比较次数要小于直接插入排序，平均性能要优于直接插入排序，时间复杂度为O(n^2)
该算法比较次数与待排序列初始排序列无关，依赖于有序序列的元素个数，插入第i个元素时比较次数为logi。折半插入排序的对象移动次数与直接排序相同，依赖对象的初始排列。

空间复杂度：

只需要一个辅助空间arr[0],因此空间复杂度为O(1)。

1.3 希尔排序

通过分析直接插入排序可以得出，待排序记录个数越少、待排序记录中逆序对越少，直接插入排序算法的效率越高。希尔排序正是通过将待排序记录分组来减少记录数量，通过对分组后的每个小组进行直接插入排序来减少逆序对的数量。

java 复制代码

public class ShellSort{
    public static void shellSort(int[] arr){
        int n=arr.length;

        //初始间隔设置为数组长度的一半，然后逐步缩小间隔
        for(int gap=n/2;gap>0;gap/=2){
            //对各个间隔分组进行插入排序
            for(int i = gap; i < n; i++){
                int temp=arr[i];
                int j=i;
            
                // 对当前元素进行插入排序（以gap为步长）
                while (j >= gap && arr[j - gap] > temp) {
                    arr[j] = arr[j - gap];
                    j -= gap;
                }
                arr[j] = temp;
        }
    }
}

时间复杂度：

最坏情况，步长序列由n/2^k 计算得出，为O(n^2)
最好情况，步长序列由下列公式计算得出，为O(n^(4/3))

空间复杂度：

仅用arr[0]作为辅助空间，因此时间复杂度为O(1)

二、交换排序

基本思想：两两比较待排序记录关键字，当两个关键字不满足次序要求时进行交换，直到整个序列满足要求为止。

2.1 冒泡排序

两两比较关键字，如逆序则交换顺序，较大关键字逐渐一端移动，直到序列有序。

java 复制代码

public class BubbleSort{
    public static void bubbleSort(int[] arr){
    int n=arr.length;

    //外层循环控制排序轮数
    for(int i=0; i < n-1; i++){
        //内层循环进行相邻元素比较和交换
        for(int j=0;j<n-1-i;j++){
            //如果前一个元素大于后一个元素，则交换
            if(arr[j] > arr[j + 1]){
                // 交换两个元素
                  int temp = arr[j];
                  arr[j] = arr[j + 1];
                  arr[j + 1] = temp;
               }
            }
        }
    }    
}

时间复杂度：

最好情况（初始序列正序），只需进行一次排序，在排序过程中进行n-1次关键字的比较，不移动记录
最坏情况（初始序列逆序），进行n-1次排序，总的关键字比较次数为 n^2 / 2 ，记录移动次数为（3n^2 ）/ 2
平均情况，比较次数和记录移动次数分别为 n^2 / 2 ,3n^2 / 4, 时间复杂度为O(n^2)

空间复杂度：

仅需arr[0]作为交换辅助空间，故空间复杂度为O(1)

2.2 快速排序

由冒泡排序改进得到，冒泡排序只对相邻两个记录进行比较，因此每次只能消除一个逆序，而快速排序一次交换可消除多个逆序，从而提高排序性能。

java 复制代码

public class QuickSort {
    
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            // 找到分区点
            int pivotIndex = partition(arr, low, high);
            
            // 递归排序左半部分
            quickSort(arr, low, pivotIndex - 1);
            // 递归排序右半部分
            quickSort(arr, pivotIndex + 1, high);
        }
    }
    
    private static int partition(int[] arr, int low, int high) {
        // 选择最后一个元素作为基准
        int pivot = arr[high];
        
        // i 指向小于基准的区域的最后一个元素
        int i = low - 1;
        
        // 遍历数组，将小于基准的元素移到左边
        for (int j = low; j < high; j++) {
            if (arr[j] < pivot) {
                i++;
                // 交换 arr[i] 和 arr[j]
                swap(arr, i, j);
            }
        }
        
        // 将基准元素放到正确位置
        swap(arr, i + 1, high);
        return i + 1; // 返回基准元素的最终位置
    }

时间复杂度： 快速排序的趟数取决于递归树的深度

最好情况（每次排序后序列被分成两个大小大致相等的子表），定位枢轴所需的时间为O(n)，总的排序时间为O(nlog2 n)
最坏情况（待排序列有序），递归树成为单支树，关键字的比较次数为n^2 / 2 ,这种情况下快速排序的速度已经退化为简单排序的水平。枢轴记录的合理选择可以避免最坏情况的出现，例如，可在待排序列中随机选择枢轴，并将枢轴交换到第一个位置。

平均情况，时间复杂度为O(nlog2 n)

空间复杂度：

快速排序时递归的，最大递归调用次数与递归树的深度一致，因此最好情况为O(log2 n)，最坏情况为O(n)

三、选择排序

基本思想：每一趟排序从待排序的记录中选出关键字最小的记录，按顺序放在已排序的记录中，直到全部排完为止。

java 复制代码

public class SelectionSort {
    
    public static void selectionSort(int[] arr) {
        int n = arr.length;
        
        // 外层循环，每次确定一个位置的最小值
        for (int i = 0; i < n - 1; i++) {
            // 假设当前位置是最小值的索引
            int minIndex = i;
            
            // 内层循环，在未排序部分中寻找真正的最小值
            for (int j = i + 1; j < n; j++) {
                // 如果找到更小的元素，更新最小值的索引
                if (arr[j] < arr[minIndex]) {
                    minIndex = j;
                }
            }
            
            // 如果最小值不在当前位置，则交换
            if (minIndex != i) {
                // 交换 arr[i] 和 arr[minIndex]
                int temp = arr[i];
                arr[i] = arr[minIndex];
                arr[minIndex] = temp;
            }
        }
    }

时间复杂度：

最好情况（正序），记录不需要移动。
最坏情况（逆序），移动3(n-1)次

无论记录的初始状态如何，所进行的关键字之间的比较次数相同，均为n^2 / 2 ，因此时间复杂度为O(n^2)

空间复杂度：

仅用arr[0]作为交换辅助空间，因此空间复杂度为O(1)

四、堆排序

每次将堆顶元素取出，与末尾元素交换，调整前n-1个元素，使其仍然成堆，重复上述过程，直到剩余元素为1时为止，即可得到非递减序列

java 复制代码

public class HeapSort {
    
    public static void heapSort(int[] arr) {
        int n = arr.length;
        
        // 步骤1：构建最大堆（从最后一个非叶子节点开始）
        // 最后一个非叶子节点的索引 = (n/2) - 1
        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }
        
        // 步骤2：一个个从堆顶取出元素（最大值），放到数组末尾
        for (int i = n - 1; i > 0; i--) {
            // 将当前堆顶元素（最大值）与数组末尾元素交换
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            
            // 重新调整堆，但这次只调整前i个元素（排除已排序的部分）
            heapify(arr, i, 0);
        }
    }
    
    // 调整以节点i为根的子树，使其成为最大堆
    private static void heapify(int[] arr, int n, int i) {
        int largest = i;        // 初始化最大值为根节点
        int left = 2 * i + 1;   // 左子节点索引
        int right = 2 * i + 2;  // 右子节点索引
        
        // 如果左子节点存在且大于根节点
        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }
        
        // 如果右子节点存在且大于当前最大值
        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }
        
        // 如果最大值不是根节点
        if (largest != i) {
            // 交换根节点和最大值节点
            int temp = arr[i];
            arr[i] = arr[largest];
            arr[largest] = temp;
            
            // 递归调整受影响的子树
            heapify(arr, n, largest);
        }
    }

时间复杂度：

堆排序平均性能接近于最坏性能，时间复杂度为O(nlog2 n)

空间复杂度：

仅用arr[0]作为交换辅助空间，空间复杂度为O(1)

五、归并排序

基本思想：假设初始序列含有n个记录，则可看成时n个有序的子序列，每个子序列的长度为1，然后两两并归，得到n/2个长度为2或1的有序子序列；如此重复，直至得到一个长度为n的有序序列为止。

java 复制代码

public class MergeSort {
    
    public static void mergeSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
        int[] temp = new int[arr.length];
        mergeSort(arr, temp, 0, arr.length - 1);
    }
    
    private static void mergeSort(int[] arr, int[] temp, int left, int right) {
        if (left < right) {
            int mid = left + (right - left) / 2;
            
            // 递归排序左半部分
            mergeSort(arr, temp, left, mid);
            // 递归排序右半部分
            mergeSort(arr, temp, mid + 1, right);
            // 合并两个有序数组
            merge(arr, temp, left, mid, right);
        }
    }
    
    private static void merge(int[] arr, int[] temp, int left, int mid, int right) {
        // 复制数据到临时数组
        for (int i = left; i <= right; i++) {
            temp[i] = arr[i];
        }
        
        int i = left;      // 左子数组的起始索引
        int j = mid + 1;   // 右子数组的起始索引
        int k = left;      // 合并后数组的起始索引
        
        // 合并两个有序数组
        while (i <= mid && j <= right) {
            if (temp[i] <= temp[j]) {
                arr[k] = temp[i];
                i++;
            } else {
                arr[k] = temp[j];
                j++;
            }
            k++;
        }
        
        // 复制左子数组剩余的元素
        while (i <= mid) {
            arr[k] = temp[i];
            i++;
            k++;
        }
        
        // 注意：右子数组的剩余元素不需要复制，因为它们已经在正确位置
    }
    
    public static void main(String[] args) {
        int[] arr = {12, 11, 13, 5, 6, 7};
        
        System.out.println("排序前的数组:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
        
        mergeSort(arr);
        
        System.out.println("\n排序后的数组:");
        for (int num : arr) {
            System.out.print(num + " ");
        }
    }
}

时间复杂度：

n个记录需要进行log2 n趟归并排序，每一趟归并，其关键字比较次数不超过n，元素移动次数都是n，因此时间复杂度为O(nlog2 n)

空间复杂度：

用顺序表实现递归时，需要和待排序记录相等的辅助存储空间，所以空间复杂度为O(n)

六、基数排序

基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。排序过程是将所有待比较数值统一为同样的数位长度，数位较短的数前面补零，然后从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。

java 复制代码

import java.util.Arrays;

public class RadixSort {
    
    // 获取数组中的最大值
    private static int getMax(int[] arr) {
        int max = arr[0];
        for (int i = 1; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        return max;
    }
    
    // 使用计数排序对指定位进行排序
    private static void countingSort(int[] arr, int exp) {
        int n = arr.length;
        int[] output = new int[n]; // 输出数组
        int[] count = new int[10]; // 计数数组，0-9
        
        // 初始化计数数组
        Arrays.fill(count, 0);
        
        // 统计每个数字出现的次数
        for (int i = 0; i < n; i++) {
            int digit = (arr[i] / exp) % 10;
            count[digit]++;
        }
        
        // 计算累计次数
        for (int i = 1; i < 10; i++) {
            count[i] += count[i - 1];
        }
        
        // 构建输出数组
        for (int i = n - 1; i >= 0; i--) {
            int digit = (arr[i] / exp) % 10;
            output[count[digit] - 1] = arr[i];
            count[digit]--;
        }
        
        // 将排序后的数组复制回原数组
        System.arraycopy(output, 0, arr, 0, n);
    }
    
    // LSD 基数排序主函数
    public static void radixSort(int[] arr) {
        if (arr == null || arr.length <= 1) {
            return;
        }
        
        // 找到最大值以确定位数
        int max = getMax(arr);
        
        // 从个位开始，对每一位进行计数排序
        for (int exp = 1; max / exp > 0; exp *= 10) {
            countingSort(arr, exp);
        }
    }