【论文笔记】MasRouter: Learning to Route LLMs for Multi-Agent Systems

论文信息

论文名称： MasRouter: Learning to Route LLMs for Multi-Agent Systems - ACL 2025
论文作者： Yanwei Yue et al. - Tongji University
论文链接： http://arxiv.org/abs/2502.11133
代码链接： https://github.com/yanweiyue/masrouter
论文关键词： Multi-Agent System Routing（MASR）、LLM Routing、Agent Role Allocation

---

研究背景

• MAS 的潜力与局限： 基于大语言模型（LLM）的多智能体系统（MAS）通过集体智慧和专业化分工，展现出超越单智能体的能力 。
• 成本与效率瓶颈： 现有的 MAS 通常使用同质化（LLM-homogeneous）的后端（如统一使用 GPT-4），这导致了巨大的 Token 开销和经济成本 。
• 现有的路由方法不足： 现有的 LLM 路由方法（如 RouteLLM、RouterDC）主要针对单智能体场景，仅关注"为查询选择哪个模型"，而忽视了 MAS 中关键的协作模式和角色分配决策 。

简单来说就是，随着 MAS 的逐渐发展，原本的只关注于 Single Agent 的更换其 Backbone 模型的路由方法已经不够了，需要一套针对 MAS 的路由方法。

将 single-agent routing 直接"套"到 MAS 上是不可行的，因为 MAS 额外引入了三类关键决策：

1. 协作模式选择（Chain / Tree / Debate / Graph 等）
2. Agent 数量与角色分工
3. 不同角色匹配不同 LLM

现有 routing 方法完全忽略了这些维度。

---

MASR（Multi-Agent System Routing）

MASR 的定义

针对提到的问题，作者首次系统性的提出了一个问题：Multi-Agent System Routing（MASR）

其目标是： 对于任意输入 query，在给定 LLM 池、角色池和协作模式集合的情况下，自动构建一个"性能---成本最优"的 MAS。

具体来说包括三类决策：

1. Collaboration Mode Determination 选择合适的多智能体通信拓扑
2. Agent Role Allocation 决定 agent 数量与角色组合
3. Agent LLM Routing 为每个 agent 分配合适的 LLM

MASR 的形式化定义

将 MAS 定义为搜索空间：

S = ( M , R , T ) \mathcal{S}=\left( \mathcal{M},\mathcal{R},\mathcal{T}\right) S=(M,R,T)

• M \mathcal{M} M: LLM 池（不同基座模型）
• R \mathcal{R} R: 角色集合（programmer, analyst, tester...）
• T \mathcal{T} T: 协作模式集合（Chain, Tree, Debate...）

所以 MASR 本质上是一个 条件概率建模问题，其中 Q Q Q 表示 查询语句：
P ( S ∣ Q ) P\left(S|Q\right) P(S∣Q)

并通过如下目标函数进行优化：

max ⁡ P ( S ∣ Q ) E ( Q , a ) ∼ D , S ∈ S ∼ P ( S ∣ Q ) [ U ( S ; Q , a ) ⏟ U t i l i t y − λ ⋅ C ( S ; Q ) ⏟ C o s t ] , \max_{P(S|Q)} \mathbb{E}{\substack{(Q,a) \sim \mathcal{D}, \\ S \in \mathcal{S} \sim P(S|Q)}} \left[ \underbrace{U(S; Q, a)}{Utility} - \lambda \cdot \underbrace{C(S; Q)}_{Cost} \right], P(S∣Q)maxE(Q,a)∼D,S∈S∼P(S∣Q) Utility U(S;Q,a)−λ⋅Cost C(S;Q) ,

所以这其实是一个 性能-成本 联合优化的随机策略学习问题，而非简单的分类问题。

---

MasRouter

再次回顾一下 MASR 是指：给定一个查询 Q \mathcal{Q} Q、一个 LLM 池 M \mathcal{M} M、 一个角色库 R \mathcal{R} R 和一个协作模式库 T \mathcal{T} T，一个理想的 MAS 路由器应能：

1. 确定最优协作模式（如 Chain、Tree、Debate）；
2. 动态分配智能体数量与角色（如"程序员"、"验证者"）；
3. 为每个智能体路由最合适的 LLM 后端（如 GPT-4、Llama3、Med-PaLM）；

从而在保证高质量响应的同时，最小化系统开销。

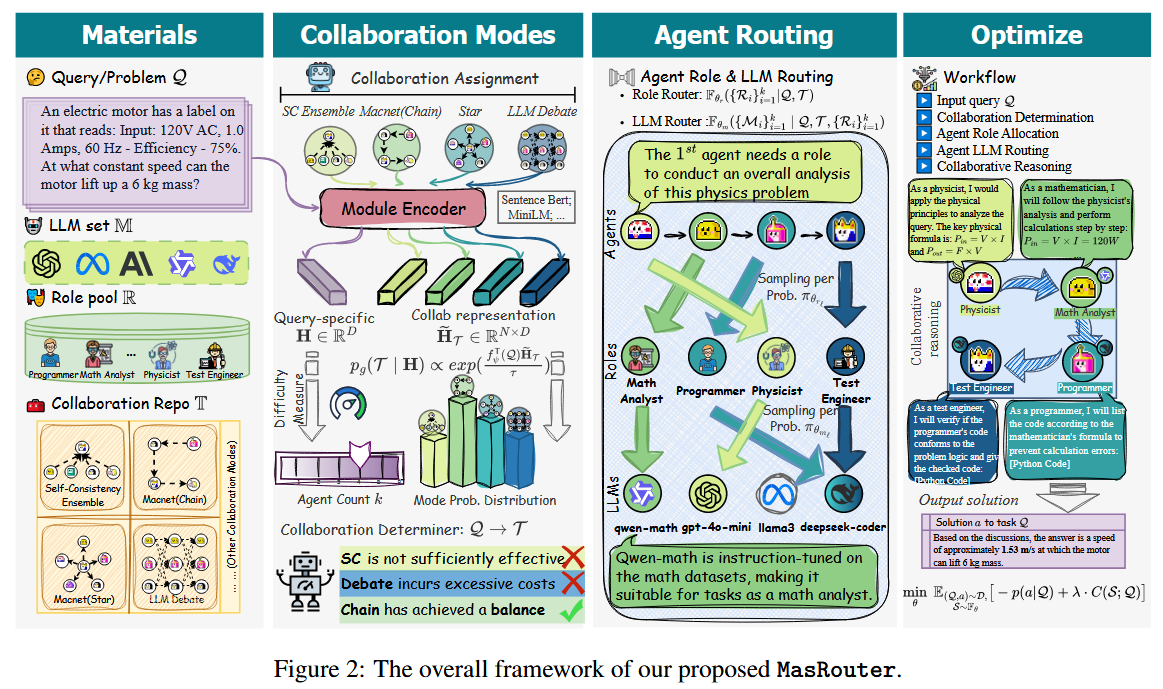
在对于 MASR 范式的定义基础上，作者提出了MasRouter。MasRouter 是一个 级联式（cascaded）控制器网络，它将 MAS 构建过程分解为三个渐进式阶段，模拟人类团队协作的逻辑：

F θ = F θ m ∘ F θ r ∘ F θ t F_{\theta} = F_{\theta_{m}} \circ F_{\theta_{r}} \circ F_{\theta_{t}} Fθ=Fθm∘Fθr∘Fθt

1. 先决定怎么合作（拓扑）Collaboration Mode Determination
2. 再决定谁来干什么（角色）Agent Role Allocation
3. 最后决定每个人用什么能力（LLM）Agent LLM Routing

为什么会设计成级联网络呢？ 我认为是作者是根据人类团队协作的逻辑将联合概率进行分解得到的：
P ( S ∣ Q ) = P ( T ∣ Q ) ⋅ P ( R ∣ Q , T ) ⋅ P ( M ∣ Q , T , R ) P\left( S|Q\right) = P\left(T |Q\right) \cdot P \left( R| Q,T \right) \cdot P \left( M| Q,T,R\right) P(S∣Q)=P(T∣Q)⋅P(R∣Q,T)⋅P(M∣Q,T,R)

在这样的分解下，很直接的我们就能想到每一个步骤之间是存在因果条件关系的，那自然会设计成一个级联网络。

那这样的设计有什么好处呢？ 在面对 MASR 这个问题时，我们会自然想到，为什么不直接得到 搜索空间 S S S，而是选择设计一个级联网络来分布计算。

那我们先假设，我们能够一次性得到，我们会有

• M M M 种 LLM
• R R R 种 角色
• T T T 种协作模式
• 最多 K K K 个 Agent

此时 MASR 的搜索空间规模近似为 :

∣ S ∣ = ∑ k = 1 K T ⏟ 拓扑 × R k ⏟ 角色分配 × N k ⏟ L L M 分配 = T ⋅ ∑ k = 1 K ( R M ) k |\mathcal{S}| = \sum_{k=1}^{K}\underbrace{T}{拓扑}\times\underbrace{R^k}{角色分配}\times\underbrace{N^k}{LLM 分配} = T \cdot \sum{k=1}^{K}\left(RM \right)^k ∣S∣=k=1∑K拓扑 T×角色分配 Rk×LLM分配 Nk=T⋅k=1∑K(RM)k

一步到位的搜索成本为:

O ( ( R M ) k ) \mathcal{O} \left(\left(RM\right)^k\right) O((RM)k)

我们会发现搜索空间呈现标准的指数级爆炸，不可学习，不可搜索。我们无法一步就得到决策。

而经过 MasRouter 建模的是：

P ( T , k , R 1 , . . . , R k , M 1 , . . . , M k ∣ Q ) = P ( T , k ∣ Q ) ⋅ ∏ i = 1 k P ( R i ∣ Q , T , R < i ) ⋅ ∏ i = 1 k P ( M i ∣ Q , T , R ) P\left(T,k,R_1,...,R_k,M_1,...,M_k|Q\right) = P\left(T,k|Q\right) \cdot \prod_{i=1}^k P\left(R_i | Q,T,R_{<i}\right) \cdot \prod_{i=1}^k P\left(M_i | Q,T,R \right) P(T,k,R1,...,Rk,M1,...,Mk∣Q)=P(T,k∣Q)⋅i=1∏kP(Ri∣Q,T,R<i)⋅i=1∏kP(Mi∣Q,T,R)

可以看出 MasRouter 的决策步骤如下：

对一个给定 query Q Q Q，一次 MAS 构建包含：

1. Step 0: 选择拓扑 T T T
2. Step 1-k: 角色分配
3. Step k+1 - 2k: 模型分配

总步数约等于 2k

那对于 每一步的 action space 大小

• 角色分配阶段
  • 每一步选择一个角色
  • action space 大小 = R R R
• 模型分配阶段
  • 每一步选择一个模型
  • action space 大小 = M M M

那其实我们把它看成搜索树

• 深度：2k
• 每层分支数：
  • 前 k 层： R R R
  • 后 k 层： M M M

对于 MasRouter 只是走其中的一条路径，而不是遍历所有路径，所以它一次 Rollout 的计算成本是：

• 角色阶段： k k k 次决策 × \times × 每次 R R R 维 softmax
• 模型阶段： k k k 次决策 × \times × 每次 M M M 维 softmax

所以决策总成本就为：

O ( k R + k M ) = O ( k ( R + M ) ) \mathcal{O}\left(kR+kM\right) = \mathcal{O}\left(k\left(R+M\right)\right) O(kR+kM)=O(k(R+M))

这样子我们的决策成本就下降到了线性水平，当然 MasRouter 并没有降低"理论组合空间大小"，它降低的是"决策时的分支复杂度"。

表示 MasRouter 的工作流程的伪代码如下：

---

Collaboration Mode Determination

该部分的技术核心：

• 作者利用变分隐变量模型（Variational Latent Variable Model）捕捉查询与协作模式之间的予以关联。
  • Query → \rightarrow → 潜变量 H H H → \rightarrow → Collaboration Mode
• 通过学习到的复杂度映射函数动态决定所需的智能体数量 k k k

论文没有直接建模 P ( T ∣ Q ) P\left(T|Q\right) P(T∣Q)，而是引入潜变量 H H H，并建模为：

P ( T ∣ Q ) = ∫ P ( T ∣ H ) P ( H ∣ Q )   d H P\left(T|Q\right) = \int P\left(T|H\right)P\left(H|Q\right) \,dH P(T∣Q)=∫P(T∣H)P(H∣Q)dH

这么做的原因，我分析有三点：

1. Query → \rightarrow → 协作模式不是确定映射
   • 对于同一道题可能：
   • 小模型 + chain 够用
   • 或者 大模型 + 单 agent 也够用
2. Query 的 结构复杂度是隐含的
   • 是否需要多视角？
   • 是否存在中间依赖？
3. H H H 可以理解为 任务的潜在推理形态 embedding

作者用一个独立 head 预测 k k k，本质是：
k = f k ( Q ) k=f_k(Q) k=fk(Q)

实际上是：

• 用一个 MLP head 输出一个连续值
• 再 discretize 到 { 1 , . . . , K m a x } \{1,...,K_{max}\} {1,...,Kmax}

这是一个连续预测再离散化的过程（便于反向传播）。

---

Agent Role Allocation

我认为这一部分是重点

作者将角色分配建模为(不是一个集合，而是序列生成)：

P ( R ∣ Q , T ) = ∏ i = 1 k P ( R i ∣ Q , T , R < i ) P\left( R|Q,T\right) = \prod_{i=1}^{k} P\left(R_i|Q,T,R_{<i}\right) P(R∣Q,T)=i=1∏kP(Ri∣Q,T,R<i)

这可以叫作自回归角色生成（是自回归分布 autoregressive），等价于：

• 用一个 decoder
• 每一步生成一个角色
• 上一步的角色作为条件输入

对于这个分布每一步在做什么？

对第 i i i 个 agent：
P ( R i ∣ Q , T , R < i ) = Softmax ( f θ ( R ) ( Q , T , R < i ) ) P\left(R_i|Q,T,R_{<i}\right) = \text{Softmax}\left(f_{\theta}^{(R)}\left(Q,T,R_{<i}\right)\right) P(Ri∣Q,T,R<i)=Softmax(fθ(R)(Q,T,R<i))

• f θ ( R ) f_{\theta}^{(R)} fθ(R): 角色分配网络
• 输出维度 = ∣ R ∣ |\mathcal{R}| ∣R∣

为什么不能把角色当成无序集合呢？

假设有角色集合：
{ P l a n n e r , C o d e r , T e s t e r } \{Planner,Coder,Tester\} {Planner,Coder,Tester}

如果是无序的：

• 无法表达"先规划 → 再编码 → 再测试"
• 模型不知道谁依赖谁

所以我们可以分析出这个设计的好处：

1. 自动学习合理角色顺序
2. 避免重复/冲突的角色
3. 角色数量天然受控与 k k k

与其他方法相比：

• AFlow：搜索角色组合（高成本）
• 手工MAS：角色顺序写死（无泛化）

---

Agent LLM Routing

对于 Single-Agent Routing 的建模为：
P ( M ∣ Q ) P\left(M|Q\right) P(M∣Q)

但是对于 MasRouter 的Routing 的建模为：
P ( M 1 , M 2 , . . . , M k ∣ Q , T , R ) P\left(M_1,M_2,...,M_k|Q,T,R\right) P(M1,M2,...,Mk∣Q,T,R)

可以看出这是一个 多变量联合分布。

作者采用 Multinomial 建模来解决这个问题

作者将 LLM 分配视为：

• 给定 k k k 个 agent
• 从 ∣ M ∣ |\mathcal{M}| ∣M∣ 个模型中
• 抽取 k k k 次 （可重复）

形式上：

P ( M 1 : k ∣ Q , T , R ) = Multinomial ( k ; p ) P\left(M_{1:k}|Q,T,R\right) = \text{Multinomial}\left(k;p\right) P(M1:k∣Q,T,R)=Multinomial(k;p)

其中：
p = Softmax ( f θ ( M ) ( Q , T , R ) ) p=\text{Softmax}\left(f_{\theta}^{(M)}\left(Q,T,R\right)\right) p=Softmax(fθ(M)(Q,T,R))

为什么这里不使用独立分类器？

如果假设独立：

P ( M 1 ) ⋅ P ( M 2 ) . . . P\left(M_1\right) \cdot P\left(M_2\right) ... P(M1)⋅P(M2)...

会出现以下问题：

• 所有agent 可能都被分配大模型（浪费资源）
• 或者都被分配小模型（性能差）

作者希望模型能够学到，关键角色用强模型，辅助角色用弱模型。

Gamma 函数的作用

作者使用的 Gamma 函数来配合 Multinomial，原因为：

Multinomial 概率中包含阶乘项：

k ! ∏ j n k ! \frac{k!}{\prod_{j}n_k!} ∏jnk!k!

作者用 Gamma 函数：
n ! = Γ ( n + 1 ) n! = \Gamma (n+1) n!=Γ(n+1)

来保证：

• agent 数量变化时
• log-probability 可微
• 可以用于 policy gradient

---

Optimization

MasRouter 用的是 策略梯度（REINFORCE）。

优化的目标为：

max ⁡ θ E S ∼ π θ ( ⋅ ∣ Q ) [ R ( S , Q ) ] \max_{\theta} \mathbb{E}{S\sim\pi{\theta}\left(\cdot|Q\right)}\left[R\left(S,Q\right)\right] θmaxES∼πθ(⋅∣Q)[R(S,Q)]

Reward 的定义

R ( S , Q ) = Perf ( S , Q ) ⏟ 任务性能 − λ Cost ( S , Q ) ⏟ t o k e n / p r i c e R\left(S,Q\right) = \underbrace{\text{Perf}\left(S,Q\right)}{任务性能} - \underbrace{\lambda\text{Cost}\left(S,Q\right)}{token/price} R(S,Q)=任务性能 Perf(S,Q)−token/price λCost(S,Q)

REINFORCE 更新公式：
∇ θ J ( θ ) = E [ R ( S , Q ) ⋅ ∇ θ log ⁡ P θ ( S ∣ Q ) ] \nabla_\theta J(\theta) = \mathbb{E} \left[ R(S, Q) \cdot \nabla_\theta \log P_\theta(S \mid Q) \right] ∇θJ(θ)=E[R(S,Q)⋅∇θlogPθ(S∣Q)]

其中：

log ⁡ P θ ( S ∣ Q ) = log ⁡ P ( T , k ∣ Q ) + ∑ i log ⁡ P ( R i ∣ ⋅ ) + ∑ i log ⁡ P ( M i ∣ ⋅ ) \log P_\theta(S \mid Q) = \log P(T, k \mid Q) + \sum_i \log P(R_i \mid \cdot) + \sum_i \log P(M_i \mid \cdot) logPθ(S∣Q)=logP(T,k∣Q)+i∑logP(Ri∣⋅)+i∑logP(Mi∣⋅)

这就要求 所有模块都是可微概率模型。

---

实验分析

性能表现

在 MMLU、GSM8K、MATH、HumanEval、MBPP 五个基准上：

• 全部取得最优性能
• 相比 RouterDC（SOTA routing）：平均提升 3.51%
• 相比强 MAS 方法（AFlow / AgentPrune）：在 MBPP 上最高 8.2% 提升

成本优势

• 在 HumanEval 上：成本从 0.363 ↓ 0.185（↓52%）
• Pareto front 上全面占优
• 训练阶段成本也显著低于搜索型 MAS

插件能力（Plug-and-Play）

MasRouter 可作为 已有 MAS 的 routing 插件：

• 不改变原有 agent 结构
• 仅替换 LLM 分配策略
• 在 MAD / MacNet 上：
  • 成本 ↓ 17%--28%
  • 性能小幅 ↑

泛化与归纳能力（Inductive）

• 新增未见过的 LLM（DeepSeek-v3）
• 无需重新训练
• 系统自动学会"用新模型解决难题"

---

总结

本篇论文定义了 MASR 问题，并提出了一个 MasRouter 的方法框架。但仍然有许多在 MAS 中存在的东西没考虑到：

1. 角色池与协作模式仍是人工定义
2. 安全性和鲁棒性没有考虑
3. 未覆盖到 RAG 和 Tool 等 Agent 会涉及的到配置。