RANSAC算法原理与应用

Σίσυφος19002026-01-19 14:53

一、RANSAC 是解决什么问题的？

👉 在含有大量离群点（Outliers）的数据中，鲁棒地估计模型参数

典型场景

  • 特征匹配中 错误匹配很多

  • 点云中 噪声 + 伪点

  • 拟合直线 / 平面 / 单应矩阵 / 基础矩阵

  • PnP 前的 2D--3D 对应点中有假点

普通最小二乘（LS）的问题：

  • 对离群点极其敏感

  • 一个坏点就能"拉歪"整个模型

RANSAC 的思想是：

宁可只用一小撮"干净点"，也不被脏点污染

宁可只用一小撮"干净点"，也不被脏点污染

宁可只用一小撮"干净点"，也不被脏点污染

二、RANSAC核心思想

随机抽最小样本 → 拟合模型 → 统计内点 → 重复 → 选内点最多的模型

利用随机采样和一致性检验的方法，来取分数据中的内点和外点，内点是指符合模型的数据，外点是指不符合模型的数据。

三、RANSAC 算法流程（标准版）

设模型参数为 θ

Step 1：随机采样（Minimal Sample Set）

  • 随机选 最小数量 的点

  • 例如：

    • 直线：2 点

    • 平面：3 点

    • 单应矩阵：4 对点

    • 基础矩阵：8 点（8-point）

Step 2：模型估计

  • 用最小样本估计模型

  • 通常是 解析解 / DLT

Step 3：一致性检测（Inlier Test）

  • 对所有点计算误差：

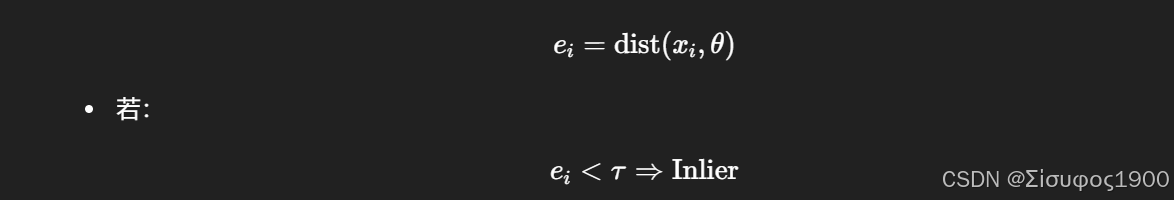
Step 4：统计内点数

  • 记录内点数量

Step 5：重复 N 次

  • 找到 内点最多 的模型

Step 6（可选）：模型重估

  • 用所有内点

  • 再做一次 最小二乘 / LM

📌 RANSAC + LM = 工程黄金搭档

四、RANSAC 数学本质

1️⃣ 目标不是最小误差，而是：

2️⃣ 内点概率驱动迭代次数

若：

  • 内点比例：w

  • 最小样本数：s

  • 成功概率：p

所需迭代次数：

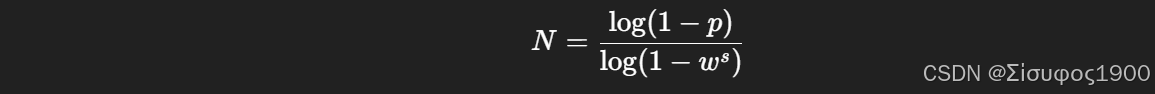
案例一RANSAC 拟合二维直线（最经典）

1️⃣ 构造数据（含离群点）

cpp 复制代码 
clc; clear; close all;

% 真实直线 y = 2x + 1
x_in = linspace(0,10,50);
y_in = 2*x_in + 1 + randn(size(x_in))*0.3;

% 离群点
x_out = rand(1,20)*10;
y_out = rand(1,20)*20;

x = [x_in x_out];
y = [y_in y_out];

figure; hold on; grid on;
scatter(x, y, 'b');
title('原始数据（含离群点）');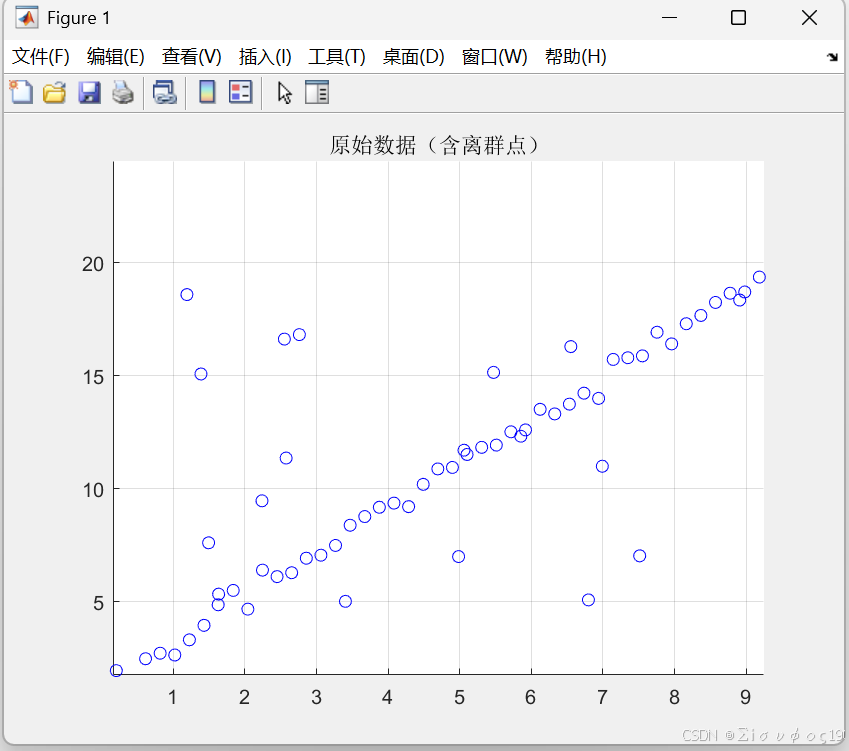

2️⃣ RANSAC 实现

cpp 复制代码 
clc; clear; close all;

% 真实直线 y = 2x + 1     50个直线上的点
x_in = linspace(0,10,50);
y_in = 2*x_in + 1 + randn(size(x_in))*0.3;

% 离群点  20个离群点
x_out = rand(1,20)*10;
y_out = rand(1,20)*20;


% 直线点+离群点=70 个
x = [x_in x_out];
y = [y_in y_out];

figure; hold on; grid on;
scatter(x, y, 'b');
title('原始数据（含离群点）');



% 迭代次数
num_iter = 1000;
% 点到直线的距离阈值判断
threshold = 0.5;



% 把最好的内点集合起来
best_inliers = [];

for i = 1:num_iter
    % 随机选2个点
    idx = randperm(length(x), 2);
    x1 = x(idx(1)); y1 = y(idx(1));
    x2 = x(idx(2)); y2 = y(idx(2));
    
    % 拟合直线 ax + by + c = 0
    a = y2 - y1;
    b = x1 - x2;
    c = x2*y1 - x1*y2;
    
    % 计算点到直线距离
    dist = abs(a*x + b*y + c) / sqrt(a^2 + b^2);
    
    inliers = find(dist < threshold);
    
    if length(inliers) > length(best_inliers)
        best_inliers = inliers;
       
    end
end


x_in = x(best_inliers);
y_in = y(best_inliers);

% 拟合 
p = polyfit(x_in, y_in, 1);

x_fit = linspace(0,10,100);
y_fit = polyval(p, x_fit);

figure; hold on; grid on;
scatter(x, y, 'b');
scatter(x_in, y_in, 'r');
plot(x_fit, y_fit, 'k', 'LineWidth',2);
legend('All points','Inliers','RANSAC Line');
title('RANSAC 直线拟合结果');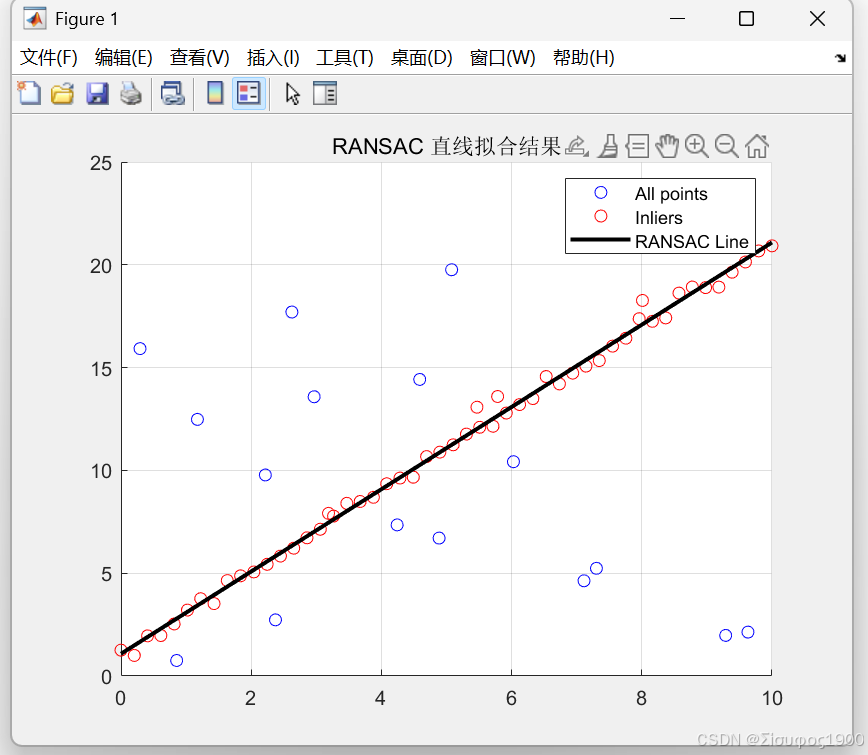

案例二 RANSAC 拟合圆

原理：

1️⃣ 圆的一般方程

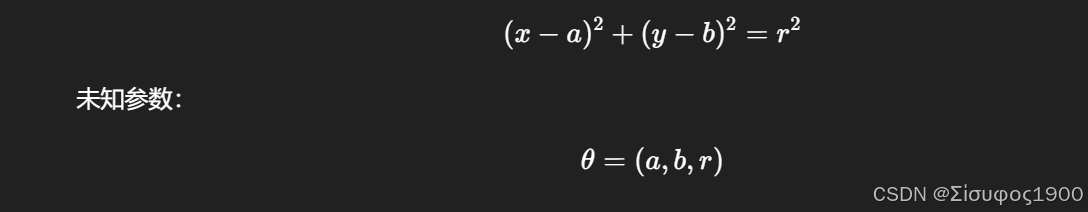
2️⃣ 最小样本数（Minimal Sample Set）

👉 3 个不共线点

（这是圆的解析最小解）

3️⃣ 点到圆的误差（RANSAC 判据）

常用误差：

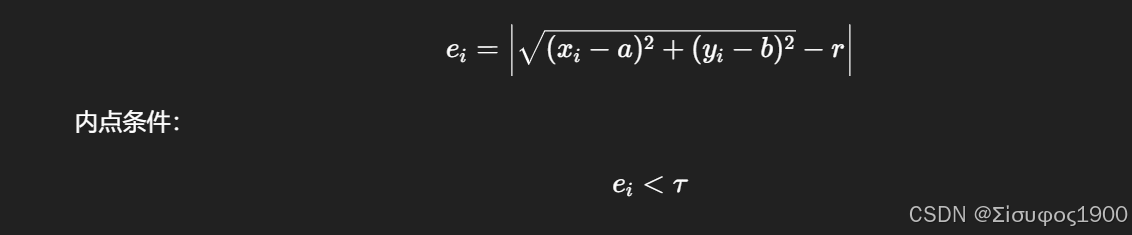
实例

1：构造测试数据（含离群点）

cpp 复制代码 
clc; clear; close all;

% 真实圆参数
a0 = 5; b0 = 4; r0 = 3;

theta = linspace(0,2*pi,80);
x_in = a0 + r0*cos(theta) + randn(size(theta))*0.05;
y_in = b0 + r0*sin(theta) + randn(size(theta))*0.05;

% 离群点
x_out = rand(1,30)*10;
y_out = rand(1,30)*10;

x = [x_in x_out];
y = [y_in y_out];

figure; hold on; axis equal; grid on;
scatter(x, y, 'b');
title('原始数据（含离群点）');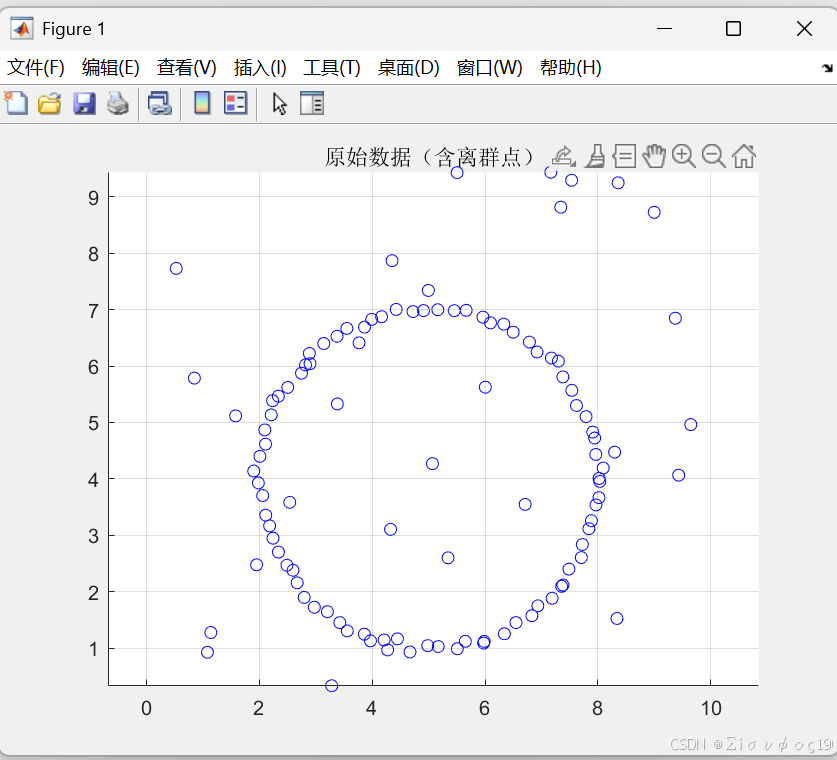

2、RANSAC 拟合圆核心代码

cpp 复制代码 
num_iter = 2000;
threshold = 0.1;

best_inliers = [];
best_circle = [];

N = length(x);

for k = 1:num_iter
    
    % 随机选 3 个点
    idx = randperm(N,3);
    x1 = x(idx(1)); y1 = y(idx(1));
    x2 = x(idx(2)); y2 = y(idx(2));
    x3 = x(idx(3)); y3 = y(idx(3));
    
    % 判断是否共线（行列式）
    if abs(det([x1 y1 1; x2 y2 1; x3 y3 1])) < 1e-3
        continue;
    end
    
    % ===== 解析求圆心和半径 =====
    A = 2*[x2-x1, y2-y1;
           x3-x1, y3-y1];
    B = [x2^2+y2^2 - x1^2-y1^2;
         x3^2+y3^2 - x1^2-y1^2];
    
    C = A\B;
    a = C(1);
    b = C(2);
    r = sqrt((x1-a)^2 + (y1-b)^2);
    
    % ===== 计算内点 =====
    dist = abs(sqrt((x-a).^2 + (y-b).^2) - r);
    inliers = find(dist < threshold);
    
    % 更新最优模型
    if length(inliers) > length(best_inliers)
        best_inliers = inliers;
        best_circle = [a b r];
    end
end

3、用内点进行最小二乘精修（强烈推荐）

cpp 复制代码 
xin = x(best_inliers);
yin = y(best_inliers);

% 代数最小二乘（线性）
A = [2*xin(:), 2*yin(:), ones(length(xin),1)];
B = xin(:).^2 + yin(:).^2;

param = A\B;

a = param(1);
b = param(2);
r = sqrt(param(3) + a^2 + b^2);

4、可视化

cpp 复制代码 
theta = linspace(0,2*pi,200);
xc = a + r*cos(theta);
yc = b + r*sin(theta);

figure; hold on; axis equal; grid on;
scatter(x, y, 'b');
scatter(x(best_inliers), y(best_inliers), 'r');
plot(xc, yc, 'k', 'LineWidth',2);
legend('All points','Inliers','RANSAC Circle');
title('RANSAC 圆拟合结果');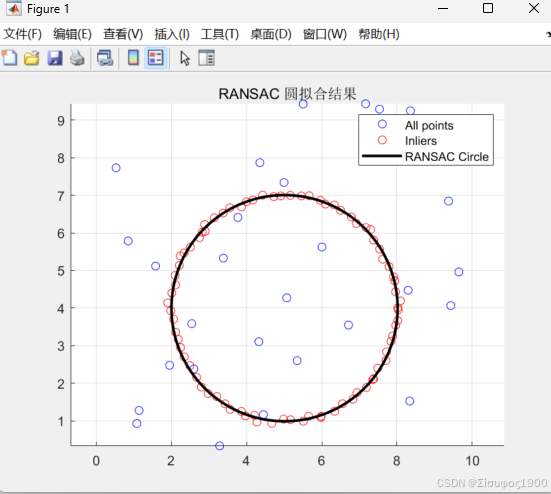

案例三、RANSAC 拟合平面

典型应用：

  • 点云地面分割（无人车）

  • 工件基准面

  • 结构光参考平面

  • ICP / PnP / BA 前的几何约束

平面数学模型

1️⃣ 平面一般式

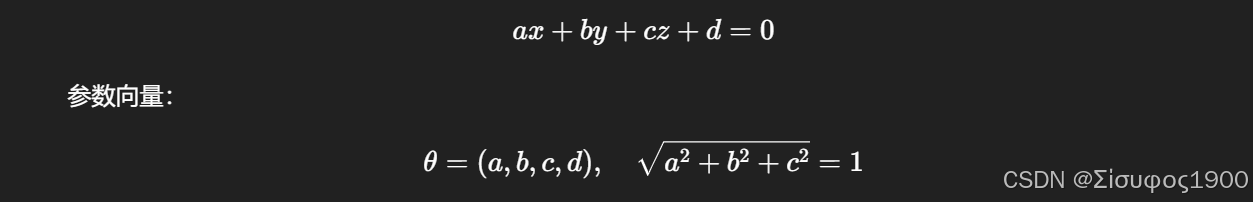
2️⃣ 最小样本数（Minimal Sample Set）

👉 3 个不共线点

3️⃣ 点到平面距离（RANSAC 判据）

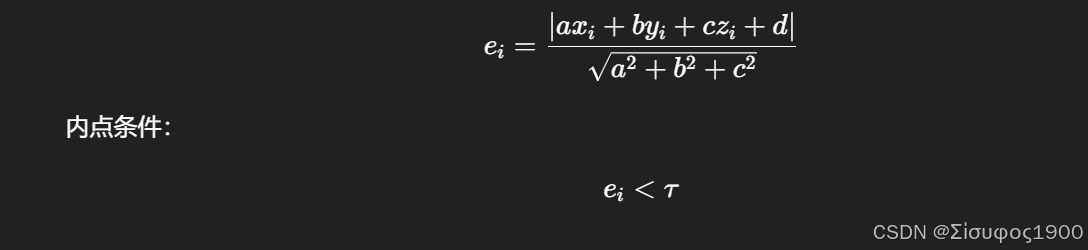
实例：

构造测试点云（含离群点）

cpp 复制代码 
clc; clear; close all;

% 真实平面：z = 0.5x + 0.2y + 1
[xg, yg] = meshgrid(linspace(0,5,20));
zg = 0.5*xg + 0.2*yg + 1 + randn(size(xg))*0.05;

% 转为点集
pts_in = [xg(:), yg(:), zg(:)];

% 离群点
pts_out = rand(80,3)*6;

pts = [pts_in; pts_out];

RANSAC 主循环

cpp 复制代码 
num_iter = 2000;
threshold = 0.1;

best_inliers = [];
best_plane = [];

N = size(pts,1);

for k = 1:num_iter
    
    % 随机选3点
    idx = randperm(N,3);
    p1 = pts(idx(1),:);
    p2 = pts(idx(2),:);
    p3 = pts(idx(3),:);
    
    % 共线判断
    v1 = p2 - p1;
    v2 = p3 - p1;
    n = cross(v1,v2);
    
    if norm(n) < 1e-6
        continue;
    end
    
    % 平面参数
    n = n / norm(n);
    d = -dot(n,p1);
    
    % 点到平面距离
    dist = abs(pts*n' + d);
    
    inliers = find(dist < threshold);
    
    if length(inliers) > length(best_inliers)
        best_inliers = inliers;
        best_plane = [n d];
    end
end

用内点进行最小二乘精修（SVD）

cpp 复制代码 
in_pts = pts(best_inliers,:);

% 去中心
centroid = mean(in_pts,1);
Q = in_pts - centroid;

% SVD
[~,~,V] = svd(Q,0);
n = V(:,end);
d = -dot(n,centroid);

best_plane = [n' d];

结果可视化

cpp 复制代码 
figure; hold on; grid on; axis equal;
scatter3(pts(:,1),pts(:,2),pts(:,3),'b.');
scatter3(in_pts(:,1),in_pts(:,2),in_pts(:,3),'r.');

% 绘制平面
[xp,yp] = meshgrid(linspace(0,5,10));
zp = -(best_plane(1)*xp + best_plane(2)*yp + best_plane(4)) / best_plane(3);
surf(xp,yp,zp,'FaceAlpha',0.5,'EdgeColor','none');

legend('All points','Inliers','Plane');
title('RANSAC 平面拟合');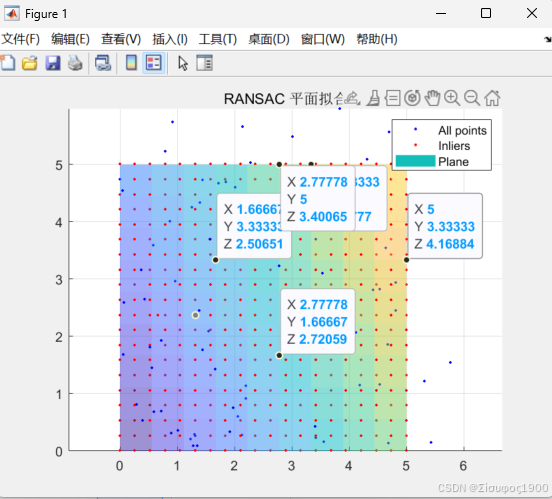

HALCON / PCL 对应参数

cpp 复制代码 
segment_planes_object_model_3d(
    ObjectModel3D,
    'distance_threshold', DistanceThreshold,
    'min_support', MinSupport,
    ObjectModel3DPlanes,
    PlaneInfo
)



pcl::SACSegmentation<pcl::PointXYZ> seg;
seg.setModelType(pcl::SACMODEL_PLANE);
seg.setMethodType(pcl::SAC_RANSAC);
seg.setDistanceThreshold(0.01);
seg.setMaxIterations(1000);
seg.setProbability(0.99);
相关推荐
我星期八休息2 小时前
MySQL数据可视化实战指南
数据库·人工智能·mysql·算法·信息可视化
程序员-King.2 小时前
day144—递归—平衡二叉树（LeetCode-110）
算法·leetcode·二叉树·递归
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #739：每日温度（单调栈、动态规划等多种实现方案详解）
算法·leetcode·面试·动态规划·单调栈·每日温度
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #394：字符串解码（递归、双栈、迭代构建等五种实现方案详解）
算法·leetcode·面试·递归·栈·字符串解码
独自破碎E2 小时前
【回溯+剪枝】字符串的排列
算法·机器学习·剪枝
Smart-佀2 小时前
FPGA入门：CAN总线原理与Verilog代码详解
单片机·嵌入式硬件·物联网·算法·fpga开发
漫随流水3 小时前
leetcode算法（513.找树左下角的值）
数据结构·算法·leetcode·二叉树
囊中之锥.4 小时前
机器学习算法详解：DBSCAN 聚类原理、实现流程与优缺点分析
算法·机器学习·聚类
AlenTech4 小时前
152. 乘积最大子数组 - 力扣（LeetCode）
算法·leetcode·职场和发展
热门推荐
01GitHub 镜像站点022025 Telegram 最新免费社工库机器人（LetsTG可[特殊字符]）搭建指南（含 Python 脚本）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Linux下V2Ray安装配置指南05Labelme从安装到标注：零基础完整指南06安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）07Claude Code Skills 实用使用手册08AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南09UV安装并设置国内源10【车载开发系列】S32 Design Studio工具安装步骤