文章目录
- 一、引言
- 二、碳纳米管手性结构
- 三、分析描述
-
-
- [2.1 轴向测量](#2.1 轴向测量)
- [2.2 径向测量](#2.2 径向测量)
-
一、引言
1研究动因:单壁碳纳米管(SWCNTs 具有卓越的电子特性,且这些特性对原子构型高度敏感,因此亟需研发可靠的SWCNTs结构测定方法。核心:综述SWCNTs结构测定技术,重点分析电子衍射图;用SAED技术( 80 k e V 80keV 80keV束能)分析单/双壁碳纳米管的衍射图,"单独分析部分衍射图会导致手性不确定",而结合多个衍射图可高置信度确定手性指数。
二、碳纳米管手性结构
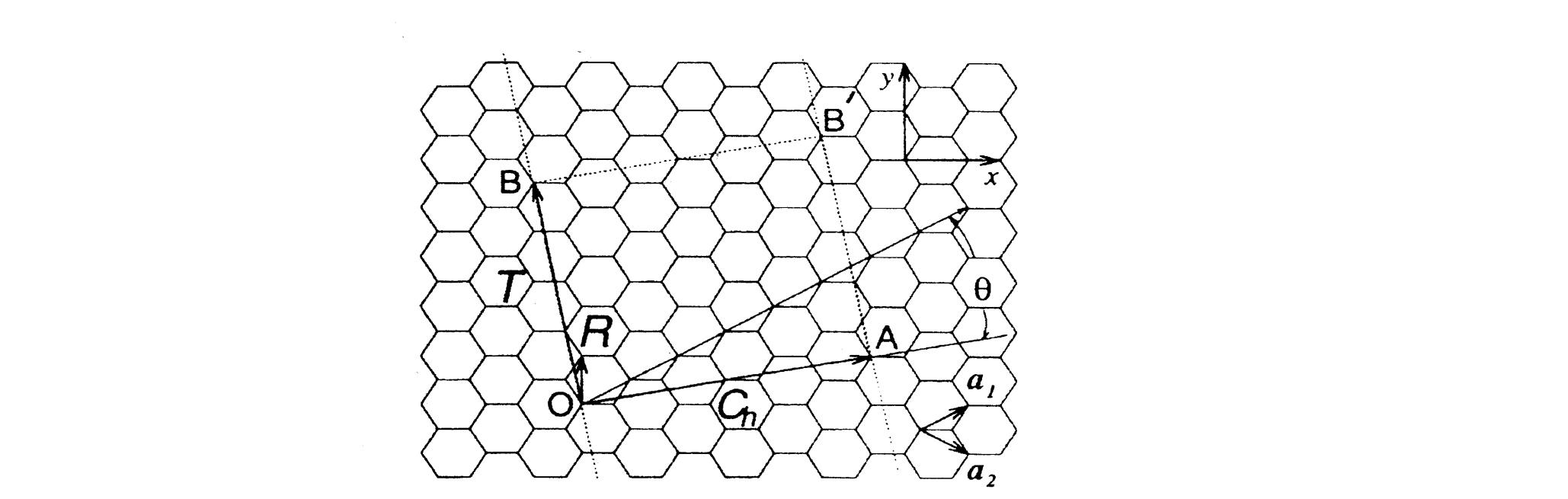
图上所示,在石墨平面中,碳原子以 sp 2 \text{sp}^2 sp2杂化形成六角环网状结构,其中 a 1 ⃗ \vec{a_1} a1 和 a 2 ⃗ \vec{a_2} a2 为石墨平面的单胞基矢,且 ∣ a 1 ⃗ ∣ = ∣ a 2 ⃗ ∣ = a = 0.246 nm |\vec{a_1}|=|\vec{a_2}|=a=0.246\,\text{nm} ∣a1 ∣=∣a2 ∣=a=0.246nm,C-C键长为 a C-C = a / 3 = 0.142 nm a_{\text{C-C}}=a/\sqrt{3}=0.142\,\text{nm} aC-C=a/3 =0.142nm。以石墨平面中任一碳原子为原点,使石墨平面绕平行于 O B OB OB方向的管轴卷曲,则 O O O点与 A A A点重合;在石墨平面上,从 O O O到 A A A的矢量即为手性矢量,其表达式为:
c h ⃗ = n a 1 ⃗ + m a 2 ⃗ ≡ ( n , m ) (2-1) \vec{c_h}=n\vec{a_1}+m\vec{a_2}\equiv(n,m) \tag{2-1} ch =na1 +ma2 ≡(n,m)(2-1)
其中 m m m、 n n n为整数,且满足 0 ≤ ∣ m ∣ ≤ n 0\leq|m|\leq n 0≤∣m∣≤n。由此可得单壁碳纳米管的周长为:
L = ∣ c h ⃗ ∣ = c h ⃗ ⋅ c h ⃗ = a n 2 + m 2 + n m (2-2) L=|\vec{c_h}|=\sqrt{\vec{c_h}\cdot\vec{c_h}}=a\sqrt{n^2+m^2+nm} \tag{2-2} L=∣ch ∣=ch ⋅ch =an2+m2+nm (2-2)
单壁碳纳米管的直径为:
d = L π = a π n 2 + m 2 + n m (2-3) d=\frac{L}{\pi}=\frac{a}{\pi}\sqrt{n^2+m^2+nm} \tag{2-3} d=πL=πan2+m2+nm (2-3)
手性角定义为 c h ⃗ \vec{c_h} ch 方向与 a 1 ⃗ \vec{a_1} a1 方向的夹角,其表达式为:
cos θ = c h ⃗ ⋅ a 1 ⃗ ∣ c h ⃗ ∣ ∣ a 1 ⃗ ∣ = 2 n + m 2 n 2 + m 2 + m n , sin θ = 3 m 2 n 2 + m 2 + m n \cos\theta=\frac{\vec{c_h}\cdot\vec{a_1}}{|\vec{c_h}||\vec{a_1}|}=\frac{2n+m}{2\sqrt{n^2+m^2+mn}}, \quad \sin\theta=\frac{\sqrt{3}m}{2\sqrt{n^2+m^2+mn}} cosθ=∣ch ∣∣a1 ∣ch ⋅a1 =2n2+m2+mn 2n+m,sinθ=2n2+m2+mn 3 m
θ = tan − 1 ∣ 3 m 2 n + m ∣ (2-4) \theta=\tan^{-1}\left|\frac{\sqrt{3}m}{2n+m}\right| \tag{2-4} θ=tan−1 2n+m3 m (2-4)
显然,锯齿管对应的手性角 θ = 0 ∘ \theta=0^\circ θ=0∘,椅型管对应的手性角 θ = 30 ∘ \theta=30^\circ θ=30∘,而手性管的手性角满足 0 ∘ ≤ θ ≤ 30 ∘ 0^\circ\leq\theta\leq30^\circ 0∘≤θ≤30∘。
三、分析描述
单壁碳纳米管(SWCNT)的结构通常用手性指数 ( n , m ) (n, m) (n,m)来描述,该指数定义了以石墨烯晶格 的单位矢量为基准、绕管周长的矢量。手性指数可完整描述管的结,单壁碳纳米管的衍射图样最容易通过考虑两片平行石墨烯 的衍射来理解:垂直于管轴入射的电子束会依次穿过两片石墨烯 (对应碳纳米管的"顶部"和"底部"壁),得到的衍射图样 是每片石墨烯衍射 的叠加。若石墨烯片相对彼此绕轴旋转,这两个衍射图样也会相对彼此旋转相同的角度(另见图1)。由于径向曲率,尖锐的衍射点会在径向方向上展宽,形成一系列被称为"层线"的线条。更准确地说,单壁碳纳米管的衍射图样是晶体倒易空间中点的投影,其中厄瓦尔德球与这些点相交。由于电子衍射中使用的是高能电子,厄瓦尔德球可近似为一个平面[24]。碳纳米管的倒易空间由一系列以管轴为中心、沿管轴方向排列的圆盘组成,厄瓦尔德平面切割这些圆盘的点便形成了层线。层线的轴向位置由单壁碳纳米管的轴向周期性决定,其径向形状由管的圆柱曲率决定[21]。
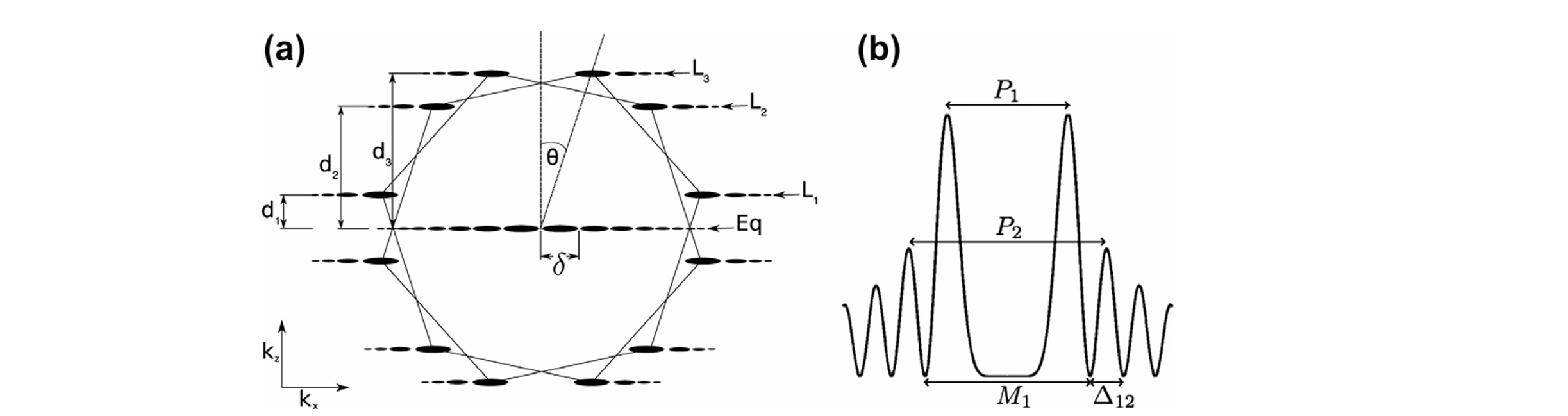
图( 1 -- a 1 -- a 1--a) 单壁碳纳米管(SWCNT)衍射图样的示意图。六边形标记的是石墨烯晶格的一级衍射斑 ,图中标注了前三条层线( L 1 -- L 3 L₁--L₃ L1--L3),同时还标注了赤道振荡(Eq)及其振荡周期 δ δ δ;图中也展示了手性角 θ θ θ,并标记了各层线的轴向距离( d 1 d₁ d1至 d 3 d₃ d3)。
(b) 其中一条层线的径向强度分布的理论形式。图中展示了一级峰与二级峰的间距( P 1 P₁ P1和 P 2 P₂ P2),同时还展示了一级极小值的间距( M 1 M₁ M1)以及振荡周期( Δ 12 Δ₁₂ Δ12)。
图 (a) 衍射花样详解
L 1 , L 2 , L 3 L1, L2, L3 L1,L2,L3:代表不同衍射层线 。这是碳纳米管衍射最独特的特征 。由于碳纳米管的管状结构,其衍射条件必须满足沿管轴方向(z方向)的周期性问题,从而产生了这些离散的层线。L1 和 L2 是最关键的两层 ,它们包含了确定手性所需的信息 。
d 1 , d 2 , d 3 d1, d2, d3 d1,d2,d3:表示从中心点到各衍射层线上衍射点的径向距离。这个距离与石墨烯的晶面间距直接相关(通过布拉格定律)。
θ θ θ:这是手性角。它被定义为碳纳米管轴线 (在图中通常是水平或垂直方向)与离其最近的石墨烯六边形 晶格方向(即其中一套衍射点,如L1层线上的点)之间的夹角。这是确定手性的最关键参数之一,其值在0°到30°之间。
δ δ δ:从中心点到特定衍射点的距离。例如,可以测量L1层线上某个点的δ值。这个值用于精确计算晶面间距 或碳纳米管的直径 。
E q Eq Eq:表示等效位置。由于碳纳米管晶格的螺旋对称性,在圆周方向上会出现多个等效的衍射点。
k x , k z kx, kz kx,kz:倒易空间的坐标轴。 k z kz kz方向通常平行于碳纳米管的轴线。
图 (b) 衍射峰剖面图详解
此图是沿着图(a)中某条线(例如,穿过L1层线上两个对称衍射点的线)所做的强度分布曲线。它将图像信息转化为可精确测量的数据。
水平轴:代表空间距离(与图 a a a中的 δ δ δ对应)。
垂直轴:代表衍射束的强度。
P 1 , P 2 P_{1}, P_{2} P1,P2:两个衍射峰的峰位。它们对应图(a)中两个特定衍射点的精确位置。
M 1 M_{1} M1:两个峰位P1和P2之间的距离。这个距离与图(a)中的某个d值直接对应。
Δ 12 \Delta_{12} Δ12:峰的分离度。在某些情况下,一个衍射点可能因为碳纳米管的结构而分裂成两个子峰, Δ 12 \Delta_{12} Δ12描述了这种分裂的程度,可用于分析碳纳米管的精细结构(如螺旋性)。
2.1 轴向测量
原则上,单壁碳纳米管的手性角 θ \theta θ可直接从衍射图样中测量;结合管的管径测量值与式( 2 − 3 2-3 2−3)、式( 2 − 4 2-4 2−4),即可确定手性指数。然而,由于管的径向曲率,衍射点的位置并不精确位于倒易空间的点上。因此,无法通过直接测量 θ \theta θ来准确确定单壁碳纳米管的结构。层线在轴向方向上的位置不受管的径向曲率影响,因此可利用层线的轴向周期性来确定单壁碳纳米管的结构。
(1) 几何手性角确定
2003年,Gao等人首次明确通过这种方式测定结构。在这项工作中,他们利用简单的几何推导 ,通过层线与赤道线的轴向距离来确定手性角,所用表达式为:
θ = tan − 1 ( 1 3 d 2 − d 1 d 3 ) = tan − 1 ( 1 3 2 d 2 − d 3 d 5 ) (3-1) \theta = \tan^{-1}\left( \frac{1}{\sqrt{3}} \frac{d_2 - d_1}{d_3} \right) = \tan^{-1}\left( \frac{1}{\sqrt{3}} \frac{2d_2 - d_3}{d_5} \right) \tag{3-1} θ=tan−1(3 1d3d2−d1)=tan−1(3 1d52d2−d3)(3-1)
其中 d i d_i di是第 i i i条层线与赤道线的距离[20]。
(2) 手性指数比值
2005年,Liu等人拓展了这一分析方法,使其能够通过测量 d i d_i di来确定手性指数的比值:
m n = d 2 − d 1 d 1 + 2 d 2 (3-2) \frac{m}{n} = \frac{d_2 - d_1}{d_1 + 2d_2} \tag{3-2} nm=d1+2d2d2−d1(3-2)
m n = d 3 + d 1 d 3 − d 1 (3-3) \frac{m}{n} = \frac{d_3 + d_1}{d_3 - d_1} \tag{3-3} nm=d3−d1d3+d1(3-3)
m n = 2 d 2 − d 3 d 3 − d 2 (3-4) \frac{m}{n} = \frac{2d_2 - d_3}{d_3 - d_2} \tag{3-4} nm=d3−d22d2−d3(3-4)
这种基于 d i d_i di距离比值的分析方法操作相对简单 ,同时还能实现"无校准的衍射图样分析"。此外, d i d_i di的比值还确保了这些分析方法不受"单壁碳纳米管轴向平面相对入射电子束倾斜 "的影响。由于衍射实验中使用的是高能电子,厄瓦尔德球可近似为一个平面;
简单的几何分析表明:当管相 对入射电子束的法线方向 倾斜时,测得的 d i d_i di距离会增大,增大的因子为 1 cos τ \frac{1}{\cos\tau} cosτ1(其中 τ \tau τ是管的轴向倾斜角。对于非常大的倾斜角( > 45 ∘ >45^\circ >45∘),厄瓦尔德球的平面近似会引入接近一个数量级的系统误差;不过,对于实际实验中 τ \tau τ的取值范围,这种近似是足够可靠的。
2007年,Jiang等人引入了另一种通过测量 d i d_i di距离来确定手性指数的技术:他们将 d i d_i di距离除以赤道振荡的周期 δ \delta δ,得到无量纲(因此无校准依赖)的参数 ξ i \xi_i ξi。利用成对的 ξ i \xi_i ξi参数可直接计算出手性指数。
n 12 = π 3 3 ⋅ ( ξ 2 + 2 ξ 1 ) ; m 12 = π 3 3 ⋅ ( ξ 2 − ξ 1 ) n 13 = π 3 3 ⋅ ( ξ 3 + ξ 1 ) ; m 13 = π 3 3 ⋅ ( ξ 3 − 2 ξ 1 ) n 23 = π 3 ⋅ ( 2 ξ 3 − ξ 2 ) ; m 23 = π 3 ⋅ ( 2 ξ 2 − ξ 3 ) (3-5) \begin{align*} n_{12}&=\frac{\pi}{3\sqrt{3}}\cdot(\xi_2 + 2\xi_1);\quad m_{12}=\frac{\pi}{3\sqrt{3}}\cdot(\xi_2 - \xi_1)\\ n_{13}&=\frac{\pi}{3\sqrt{3}}\cdot(\xi_3 + \xi_1);\quad m_{13}=\frac{\pi}{3\sqrt{3}}\cdot(\xi_3 - 2\xi_1)\\ n_{23}&=\frac{\pi}{\sqrt{3}}\cdot(2\xi_3 - \xi_2);\quad m_{23}=\frac{\pi}{\sqrt{3}}\cdot(2\xi_2 - \xi_3) \end{align*} \tag{3-5} n12n13n23=33 π⋅(ξ2+2ξ1);m12=33 π⋅(ξ2−ξ1)=33 π⋅(ξ3+ξ1);m13=33 π⋅(ξ3−2ξ1)=3 π⋅(2ξ3−ξ2);m23=3 π⋅(2ξ2−ξ3)(3-5)
此处下标对应计算中所用的 d i d_i di距离对,且 n 12 = n 13 = n 23 = n n_{12}=n_{13}=n_{23}=n n12=n13=n23=n、 m 12 = m 13 = m 23 = m m_{12}=m_{13}=m_{23}=m m12=m13=m23=m。以这种方式计算得到的手性指数,虽不依赖衍射图样的校准,但会受单壁碳纳米管(SWCNT)轴向平面相对入射电子束的倾斜影响。因此,测得的 ξ i \xi_i ξi值会比真实值大 1 cos τ \frac{1}{\cos\tau} cosτ1倍,轴向倾斜也会导致 n i , j n_{i,j} ni,j与 m i , j m_{i,j} mi,j的计算结果出现非整数值。
2.2 径向测量
关于单根单壁碳纳米管电子衍射的更完整描述,由秦于1994年首次提出------该描述将碳纳米管视为一系列分子螺旋。在这一框架下,每条层线的径向强度分布由贝塞尔函数的平方描述,而贝塞尔函数的阶数与碳纳米管的手性指数直接相关:
I 1 ( X ) ∝ ∣ J n + m ( π D 0 X ) ∣ 2 I 2 ( X ) ∝ ∣ J n ( π D 0 X ) ∣ 2 I 3 ( X ) ∝ ∣ J m ( π D 0 X ) ∣ 2 I 4 ( X ) ∝ ∣ J n − m ( π D 0 X ) ∣ 2 (3-6) \begin{align*} I_1(X) &\propto \left|J_{n+m}(\pi D_0 X)\right|^2\\ I_2(X) &\propto \left|J_{n}(\pi D_0 X)\right|^2\\ I_3(X) &\propto \left|J_{m}(\pi D_0 X)\right|^2\\ I_4(X) &\propto \left|J_{n-m}(\pi D_0 X)\right|^2 \end{align*} \tag{3-6} I1(X)I2(X)I3(X)I4(X)∝∣Jn+m(πD0X)∣2∝∣Jn(πD0X)∣2∝∣Jm(πD0X)∣2∝∣Jn−m(πD0X)∣2(3-6)
其中 I i ( X ) I_i(X) Ii(X)是第 i i i条层线的径向强度分布, D 0 D_0 D0是单壁碳纳米管的管径, X X X是径向方向的倒易空间距离。在该分子螺旋模型中,赤道振荡的径向强度 I eq I_{\text{eq}} Ieq可通过零阶贝塞尔函数的平方描述:
I eq ∝ ∣ J 0 ( π D 0 X ) ∣ 2 (3-7) I_{\text{eq}} \propto \left|J_0(\pi D_0 X)\right|^2 \tag{3-7} Ieq∝∣J0(πD0X)∣2(3-7)
对于 x ≫ 0 x \gg 0 x≫0,零阶贝塞尔函数 J 0 ( x ) J_0(x) J0(x)可近似为[41]:
J 0 ( x ) = 2 π x cos ( x − π 4 ) (3-8) J_0(x) = \sqrt{\frac{2}{\pi x}} \cos\left(x - \frac{\pi}{4}\right) \tag{3-8} J0(x)=πx2 cos(x−4π)(3-8)
当 x = ( j − 1 4 ) π x = \left(j - \frac{1}{4}\right)\pi x=(j−41)π((j)为整数)时,式(10)的值为零。本案例中 x = π D 0 X x = \pi D_0 X x=πD0X,因此单壁碳纳米管的管径可通过赤道振荡的周期 δ \delta δ近似得到:
D 0 = 1 δ (3-9) D_0 = \frac{1}{\delta} \tag{3-9} D0=δ1(3-9)
特定阶数贝塞尔函数的振荡周期是唯一的。峰间距的比值定义为:
R p = P 1 P 2 (3-10) R_p = \frac{P_1}{P_2} \tag{3-10} Rp=P2P1(3-10)
其中 P 1 P_1 P1与 P 2 P_2 P2分别是一阶峰与二阶峰的间距(见图1)。2005年刘与秦首次提出:某条层线对应的主导贝塞尔函数的阶数,可通过测量 P 1 P_1 P1与 P 2 P_2 P2、计算 R p R_p Rp并与理论值对比来确定。随着贝塞尔函数阶数的增加,理论 R p R_p Rp值之间的差异会减小,因此需要非常精确地测量 P 1 P_1 P1与 P 2 P_2 P2,才能确定高阶贝塞尔函数。
江及其合作者在2006年的后续研究中解决了这一局限。他们提出:通过使用一阶峰( P 1 P_1 P1)或一阶极小值( M 1 M_1 M1)与前两个极小值之间的距离( Δ 12 \Delta_{12} Δ12,见图1)的比值,可更准确地确定高阶贝塞尔函数:
R P D = P 1 Δ 12 (3-11) R_{PD} = \frac{P_1}{\Delta_{12}} \tag{3-11} RPD=Δ12P1(3-11)
R M D = M 1 Δ 12 (3-12) R_{MD} = \frac{M_1}{\Delta_{12}} \tag{3-12} RMD=Δ12M1(3-12)
单壁碳纳米管的轴向平面相对入射电子束偏离法线方向的任何倾斜,都会导致径向强度分布中峰的位置发生变化[24,25]。对于高阶贝塞尔函数,可通过以下表达式对每条层线的径向距离进行缩放来修正这一影响:
X ′ = d i 2 sin 2 τ + X 2 L λ (3-13) X' = \frac{\sqrt{d_i^2 \sin^2\tau + X^2}}{L\lambda} \tag{3-13} X′=Lλdi2sin2τ+X2 (3-13)
其中 d i d_i di是层线在轴向方向的距离, τ \tau τ是碳纳米管的轴向倾斜角, λ \lambda λ是入射电子的波长, L L L是样品与成像平面之间的距离 ( L λ (L\lambda (Lλ的乘积通常被称为显微镜的相机常数)。不过正如江等人所指出的:对于低阶贝塞尔函数,仅6°的管倾斜就会导致径向强度分布中最强的峰发生合并,进而使贝塞尔函数的赋值失败。
在现有文献中,单根单壁碳纳米管的手性指数已通过上述每种技术得到可靠确定,同时也可通过与模拟结果对比来确定------不过我们在此不讨论模拟相关内容。