神经网络相较于前面的决策树等,是用于解决非线性问题的。
5.1神经元模型
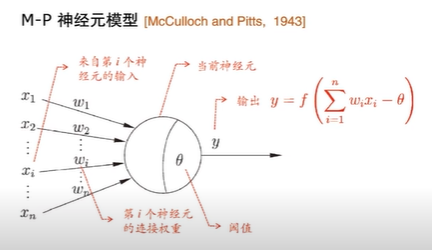
阈值其实可以理解为b,其中那个f(x)函数也就是激活函数,其本身也是带"动态阈值"的非线性判断机制。
5.2感知器与多层网络
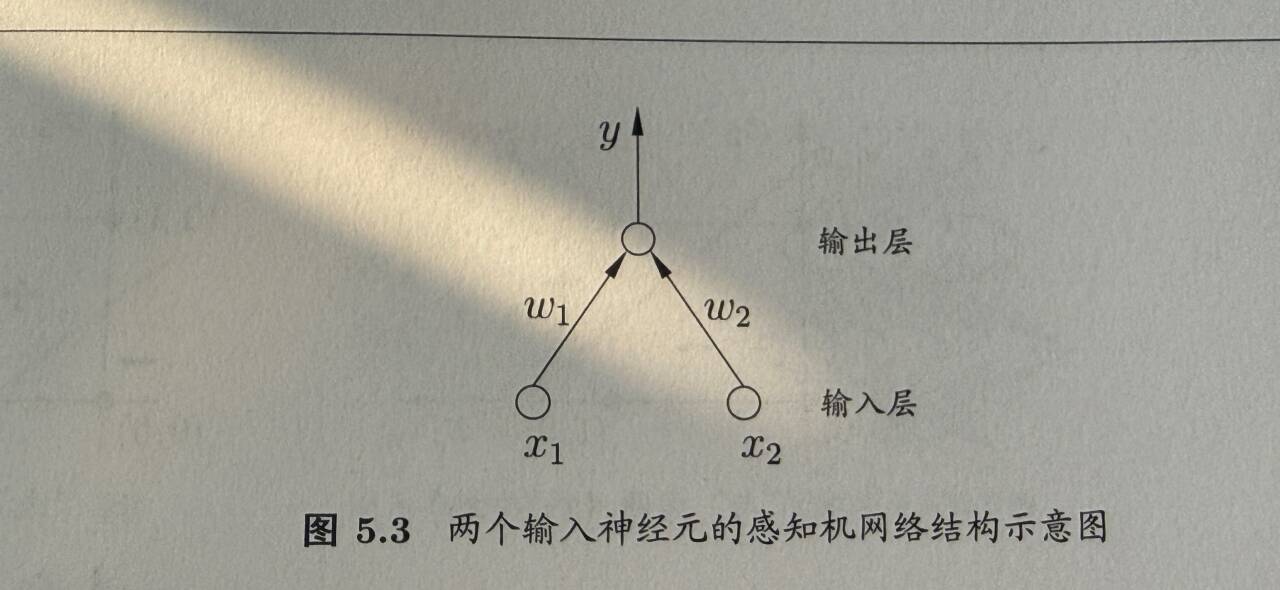
经典感知器就是由输入层和输出层两层神经元构成的简单线性分类模型,没有隐藏层,其实单个神经元就等价于一个最简单的感知器。
它的运行逻辑和神经元计算一致:输入层接收特征值,与权重相乘后加偏差得到净输入,再通过硬阈值激活函数(比如大于阈值输出1,否则输出0)得到最终分类结果。
需要注意的是,这种两层感知器只能解决线性可分的问题(比如简单的与、或运算),无法处理异或这类线性不可分的任务------这也是后来多层神经网络(引入隐藏层)被提出的重要原因。
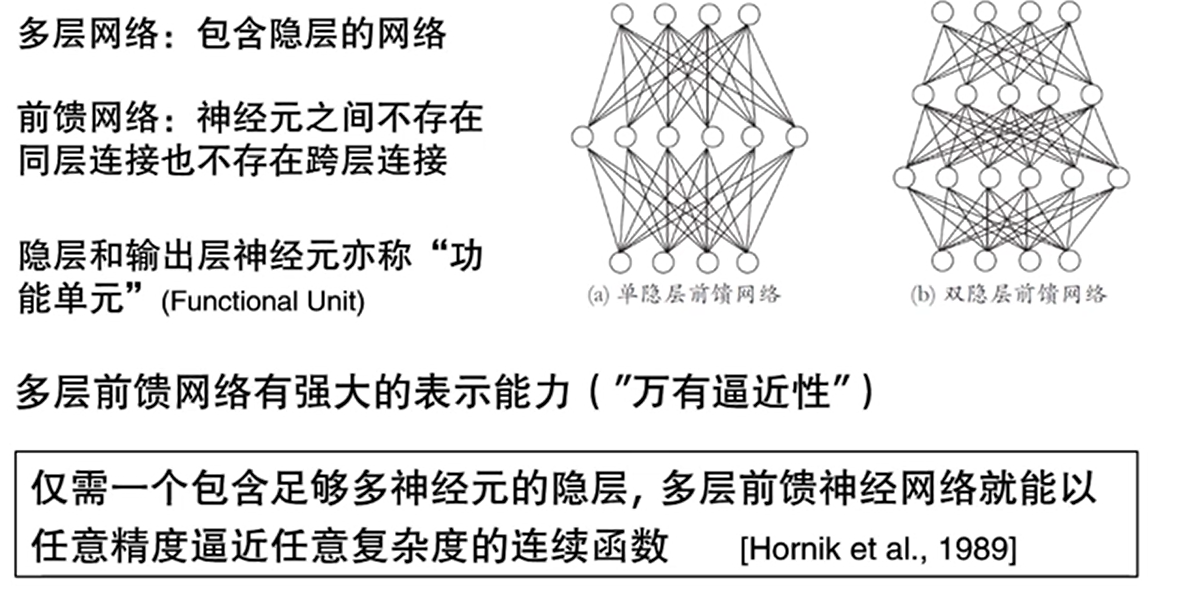
多层神经网络

5.3误差逆传播算法
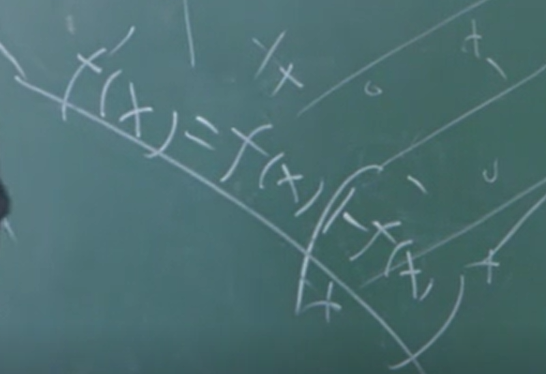
sigmoid函数求导有趣现象,如上。

反向传播主要是调整w和b使得误差处于小于阈值的范围。反向传播计算得到偏导后需要更新参数,涉及到梯度下降,前面有讲过,如下:

BP算法防止过拟合的两种做法,正则化加上右部分也相当于让权重更小,更平滑。
5.4全局最小和局部最小

这部分没有什么拓展,看书上三种方式即可。
5.5其他神经网络
RBF网络:
一种三层前馈神经网络,主打局部逼近,训练速度快于全局逼近的BP网络,常用于函数拟合、分类、回归任务。结构:输入层→隐含层→输出层,隐含层是核心,激活函数为径向基函数(最常用高斯函数,也有薄板样条等)
ART网络:
强调ART是无监督增量聚类神经网络,核心优势是抗遗忘+实时学习,解决传统聚类"一次训练,无法新增类别"的痛点。重点讲解比较层(C层)、识别层(R层)、重置模块的作用:C层负责输入样本与模板的匹配计算,R层执行神经元竞争选出获胜类别,重置模块根据警戒参数判断"匹配/重置"。
SOM网络:
一种无监督竞争型神经网络,核心功能是高维数据降维+拓扑保序聚类,能将高维输入映射到低维(多为二维)拓扑空间,同时保留数据的邻域关系。结构:输入层+竞争层(输出层),竞争层神经元按网格状排列(如矩形、六边形),每个神经元对应一个高维权重向量。
级联相关网络:
一种构造性前馈神经网络,无需预先设定隐含层节点数和层数,通过动态添加最优隐含节点的方式自主构建网络结构,主打高效监督学习,适用于分类、回归任务。
初始化:先构建只有输入层和输出层的最简网络,训练输出层权重。添加隐含节点:计算候选节点与输入数据、输出误差的相关性,选择相关性最高的候选节点加入隐含层,该节点权重固定不再更新。冻结与扩展:新增节点与输入层、输出层建立连接,训练新的输出层权重;重复"选节点-加节点-训权重"步骤,直到模型性能达标。
Elman网络:
一种简单的递归神经网络(RNN),有环状结构,专为处理时序数据设计,通过引入"承接层"实现短期记忆,擅长捕捉序列数据的上下文依赖关系。
包含四层:输入层→隐含层→承接层→输出层。承接层会存储上一时刻隐含层的输出,作为下一时刻隐含层的额外输入,相当于"短期记忆单元";隐含层常用 Sigmoid 或 tanh 激活函数,输出层多为线性或 Softmax 激活。
Boltzmann机:
一种基于能量函数的随机递归神经网络,是典型的概率生成模型,核心用于学习复杂数据的概率分布,无监督特征提取。
包含可见层(输入输出层,对应数据特征)和隐藏层(特征提取层),层内、层间神经元均为双向连接(所有神经元双向连接,可以反馈调整),神经元状态为二值(0/1),状态取值由概率函数(Sigmoid)决定。