HyperD: Hybrid Periodicity Decoupling Framework for Traffic Forecasting

现存方法的局限性：

周期性建模隐含化：传统趋势 - 季节性分解方法将周期性信息拆分到趋势和季节组件中，破坏了其跨时间尺度和空间位置的统一结构，无法直接建模连贯的周期性模式。
分解过程不可学习：传统分解方法为固定规则驱动，效率低且易导致组件错位，难以适配复杂交通场景的动态变化。
单尺度周期性建模：部分新兴方法（如 CycleNet）仅能处理单一尺度周期性，未充分利用多尺度周期信息，且缺乏对时空交互关系的有效建模。

HyperD 框架的创新：

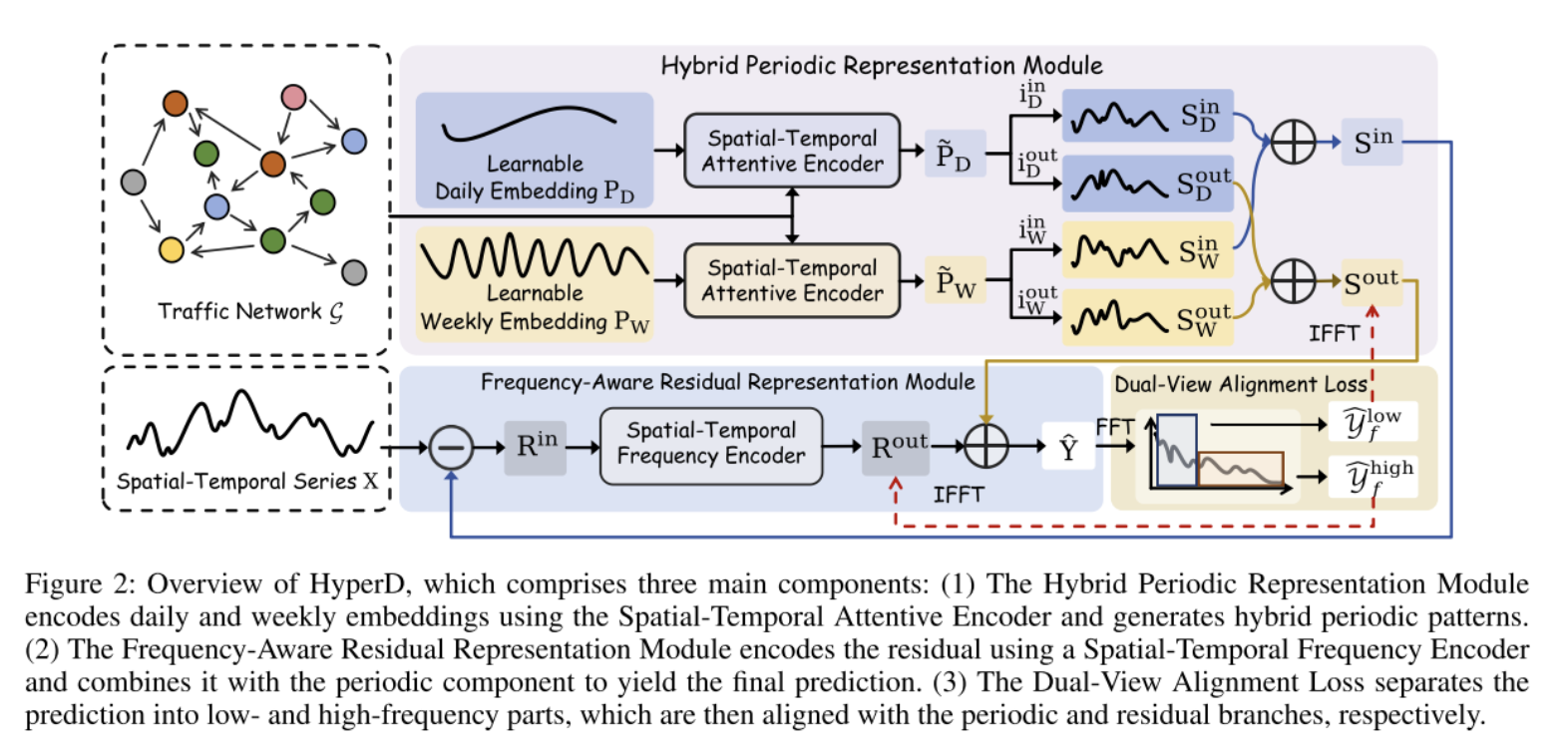
将交通数据显式解耦 为周期性组件（捕捉日、周等稳定周期模式 ）和残差组件（捕捉高频非规律波动），通过专用模块分别建模，并引入损失函数保证组件语义分离，最终融合两部分输出得到预测结果。

混合周期性表示模块

时空注意力编码器（STAE）: 捕获节点间空间关联和周期内长程时间依赖

时间维度：将每个时间步视为 Query，捕捉周期内部的长程演变规律。

空间维度：将每个节点视为 Query，捕捉不同位置之间超越物理连接的全局空间模式。

混合周期模式

元数据准备：对于每一个时间步（Time Step），模型需要知道两个信息:

Time of Day (ToD)：现在是一天中的第几个时间片？（例如：14:30 是第几步）
Day of Week (DoW)：今天是周几？（例如：周一、周二...）

索引计算:

每日索引 (iDi_DiD) ：直接等于 ToD。它负责在 P~D\tilde{P}_DP~D（每日嵌入）中定位。比如"早高峰"在每天的索引位置是固定的。

每周索引 (iWi_WiW) ：计算公式为 iW=ToD+DoW×LDi_W = \text{ToD} + \text{DoW} \times L_DiW=ToD+DoW×LD。

每周嵌入 P~W\tilde{P}_WP~W 实际上是一个长度为 7×2887 \times 2887×288 的长向量（或矩阵）。这个公式将二维的"周几+时间"展平成了一维索引，从而区分"周一的早高峰"和"周日的早高峰"。

检索与聚合：

针对**SinS^{in}Sin**：

使用 iDi_DiD 从每日嵌入 P~D\tilde{P}_DP~D 中切片，得到 SDS_DSD（每日分量）
使用 iWi_WiW 从每周嵌入 P~W\tilde{P}_WP~W 中切片，得到 SWS_WSW（每周分量）
直接相加

针对SoutS^{out}Sout:

确定时间 ：对于未来要预测的每一个时间点 ttt（从 T1+1T_1+1T1+1 到 T1+T2T_1+T_2T1+T2）。
检索嵌入（Retrieve） ：
- 根据未来的时间点（比如"明天上午8:00"），去每日嵌入表 P~D\tilde{P}_DP~D 中查出对应的特征向量 SDoutS^{out}_DSDout 。
- 根据未来的日期（比如"明天是周五"），去每周嵌入表 P~W\tilde{P}_WP~W 中查出对应的特征向量 SWoutS^{out}_WSWout 。
聚合（Aggregate） ：将两者相加，得到 Sout=SDout+SWoutS^{out} = S^{out}_D + S^{out}_WSout=SDout+SWout 。

频率感知残差表示模块

时空频率编码器（STFE）

将残差转换至频域，通过复数值MLP建模频率特异性时空行为，再转回时域，高效捕捉高频动态。

流程概览： 输入残差 -> 升维 -> 空间 FFT -> 复数 MLP -> 空间 IFFT -> 时间 FFT -> 复数 MLP -> 时间 IFFT -> 输出

双视角对齐损失

为避免周期性组件与残差组件语义重叠，保证解耦有效性：

频率分割 ：对最终预测结果 Y^\hat{Y}Y^（它是 SoutS^{out}Sout 和 RoutR^{out}Rout 的和）执行FFT，按阈值 FlowF_{low}Flow 分割为低频部分(Y^flow\hat{Y}_f^{low}Y^flow)（对应周期性模式）和高频部分(Y^fhigh\hat{Y}_f^{high}Y^fhigh) （对应残差模式）。

对齐约束 ：通过MSE损失 让低频部分与 SoutS^{out}Sout对齐，高频部分与RoutR^{out}Rout对齐，公式为 Loss=MSE(低频分量,Sout)+MSE(高频分量,Rout)\text{Loss} = \text{MSE}(\text{低频分量}, S^{out}) + \text{MSE}(\text{高频分量}, R^{out})Loss=MSE(低频分量,Sout)+MSE(高频分量,Rout) 。

总损失 ：L=Lpred+α∗Ldva\mathcal{L} = \mathcal{L}{pred} + \alpha * \mathcal{L}{dva}L=Lpred+α∗Ldva，其中 α\alphaα 是一个权重系数，用来平衡预测准确度和解耦程度。其中，预测损失 (Lpred\mathcal{L}_{pred}Lpred) ：预测值 Y^\hat{Y}Y^ 和真实值 YgtY^{gt}Ygt 之间的差异。