❶由来和简介
正交实验用例设计法,是由数理统计学中正交实验方法进化出的一种测试多条件输入的用例设计方法。
L **n**(m **k**)
plain
把所有参与实验、影响结果的条件称为因子。
把影响实验因子的取值或输入称为因子的水平。
L代表是正交表
n代表试验次数或正交表的行数
k代表最多可安排影响指标因素的个数或正交表的列数
m表示每个因素水平数
n=k*(m-1)+1根据实验数据的正交性从全面实验数据中挑选出部分具有代表性的点进行实验,这些点具有"均匀分散、整齐可比"的特点。
plain
1-整齐可比
在同一张正交表中,每个因子的每个水平出现的次数完全相同
这就保证在各个水平中最大限度的排除了其他因子水平的干扰
因此能最有效地进行比较,容易找到好的试验条件
2-均匀分散
在同一张正交表中,任意两列(两个因子)的水平搭配(横向形成的数字对)是完全相同的
这就保证了实验条件均匀分散在因素水平的完全组合中
因此具有很强的代表性,容易得到好的试验条件❷四种情况
1:因子数与水平数与正交实验表相等
假设"初步正交表":
| 水平\因子 | 内核 | 操作系统 | 分辨率 | 应用服务器 |
|---|---|---|---|---|
| 1 | Trident | Windows | 1920×1080 | Tomcat |
| 2 | Chromium | MacOS | 1366×768 | websphere |
| 3 | Gecko | Linux | 1440×900 | Weblogic |
①分析需求获取因子水平:
共有4个测试参数,且每个因子取值都是3。
②根据因子水平选择正交表
可以直接采用4因子3水平正交表。
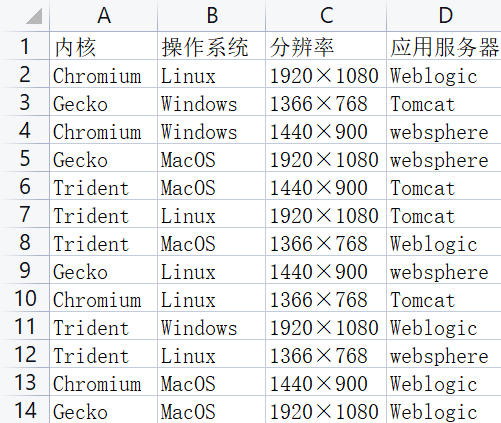
| 实验号\列号 | 1 内核 | 2 操作系统 | 3 分辨率 | 4 应用服务器 |
|---|---|---|---|---|
| 1 | Trident | Windows | 1920×1080 | Tomcat |
| 2 | Trident | MacOS | 1366×768 | websphere |
| 3 | Trident | Linux | 1440×900 | Weblogic |
| 4 | Chromium | Windows | 1366×768 | Weblogic |
| 5 | Chromium | MacOS | 1440×900 | Tomcat |
| 6 | Chromium | Linux | 1920×1080 | websphere |
| 7 | Gecko | Windows | 1440×900 | websphere |
| 8 | Gecko | MacOS | 1920×1080 | Weblogic |
| 9 | Gecko | Linux | 1366×768 | Tomcat |
test.txt:
plain
内核:Trident,Chromium,Gecko
操作系统:Windows,MacOS,Linux
分辨率:1920×1080,1366×768,1440×900
应用服务器:Tomcat,websphere,Weblogictest.xls:
*2:因子数与正交实验表因子数不符
假设"初步正交表":
| 水平\因子 | 账号 | 账号状态 | 用户 | 性别 | 时间 |
|---|---|---|---|---|---|
| 1 | 输入 | 输入 | 输入 | 输入 | 输入 |
| 2 | 不输入 | 不输入 | 不输入 | 不输入 | 不输入 |
上述需求中,发现初步正交表为5因子2水平,然后选择相应匹配的正交表,但正交表只有3因子2水平、7因子2水平、11因子2水平等更高的正交表。
在水平数相同时,选择因子数稍大于输入参数个数,且实验次数最少的正交表,显然,3因子2水平不符合要求,剩下的7因子3水平与11因子2水平相比:7因子2水平实验次数是8次,11因子2水平实验次数是12次。7因子2水平的实验次数更少,故选择7因子2水平正交表。
| 实验号\列号 | 1 账号 | 2 账号状态 | 3 用户 | 4 性别 | 5 时间 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 输入 | 输入 | 输入 | 输入 | 输入 | 1 | 1 |
| 2 | 输入 | 输入 | 输入 | 不输入 | 不输入 | 2 | 2 |
| 3 | 输入 | 不输入 | 不输入 | 输入 | 输入 | 2 | 2 |
| 4 | 输入 | 不输入 | 不输入 | 不输入 | 不输入 | 1 | 1 |
| 5 | 不输入 | 输入 | 不输入 | 输入 | 不输入 | 1 | 2 |
| 6 | 不输入 | 输入 | 不输入 | 不输入 | 输入 | 2 | 1 |
| 7 | 不输入 | 不输入 | 输入 | 输入 | 不输入 | 2 | 1 |
| 8 | 不输入 | 不输入 | 输入 | 不输入 | 输入 | 1 | 2 |
多余因子6、7抛弃,再补充5因子全取2的情况,得到最终的正交表:
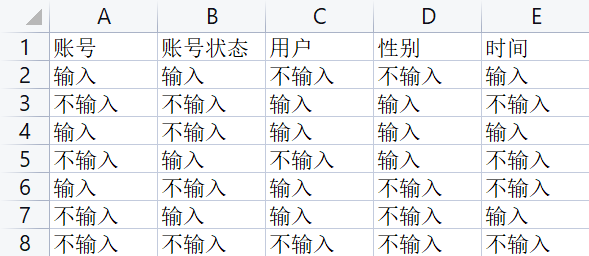
| 实验号\列号 | 1 账号 | 2 账号状态 | 3 用户 | 4 性别 | 5 时间 |
|---|---|---|---|---|---|
| 1 | 输入 | 输入 | 输入 | 输入 | 输入 |
| 2 | 输入 | 输入 | 输入 | 不输入 | 不输入 |
| 3 | 输入 | 不输入 | 不输入 | 输入 | 输入 |
| 4 | 输入 | 不输入 | 不输入 | 不输入 | 不输入 |
| 5 | 不输入 | 输入 | 不输入 | 输入 | 不输入 |
| 6 | 不输入 | 输入 | 不输入 | 不输入 | 输入 |
| 7 | 不输入 | 不输入 | 输入 | 输入 | 不输入 |
| 8 | 不输入 | 不输入 | 输入 | 不输入 | 输入 |
| 9 | 不输入 | 不输入 | 不输入 | 不输入 | 不输入 |
test.txt:
plain
账号:输入,不输入
账号状态:输入,不输入
用户:输入,不输入
性别:输入,不输入
时间:输入,不输入test.xls:
*3:水平数与正交实验表水平数不符
假设"初步正交表":
| 水平\因子 | 查询类别 | 查询方式 | 子类别 |
|---|---|---|---|
| 1 | 产品用途 | 简单 | 日常用品 |
| 2 | 产品材质 | 组合 | 家居装修 |
| 3 | 条件 |
上述需求中,发现其初步正交表可能为2因子2水平和1因子3水平,但经过对比正交表发现并无这样的正交表,预期最接近的正交表是3因子2水平及4因子3水平,但4因子3水平的实验次数是9,而3因子2水平的实验次数是4,但需求中有一项的水平是3,此时可通过先合并水平再扩展水平的方法选择正交表。
根据初步正交表,首先将查询方式中的3个水平合并为2个水平,"简单"为1,"组合"+"条件"为2,则满足3因子2水平正交表。
| 实验号\列号 | 1 查询类别 | 2 查询方式 | 3 子类别 |
|---|---|---|---|
| 1 | 产品用途 | 简单 | 日常用品 |
| 2 | 产品用途 | 组合+条件 | 家居装修 |
| 3 | 产品材质 | 简单 | 家居装修 |
| 4 | 产品材质 | 组合+条件 | 日常用品 |
因为"组合+条件"是两个水平的合并,因此最终的正交表为:
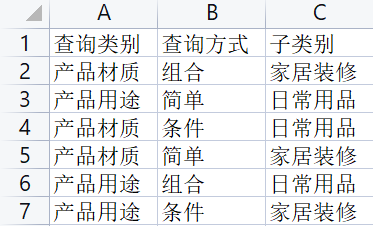
| 实验号\列号 | 1 查询类别 | 2 查询方式 | 3 子类别 |
|---|---|---|---|
| 1 | 产品用途 | 简单 | 日常用品 |
| 2 | 产品用途 | 组合 | 家居装修 |
| 3 | 产品用途 | 条件 | 家居装修 |
| 4 | 产品材质 | 简单 | 家居装修 |
| 5 | 产品材质 | 组合 | 日常用品 |
| 6 | 产品材质 | 条件 | 日常用品 |
test.txt:
plain
查询类别:产品用途,产品材质
查询方式:简单,组合,条件
子类别:日常用品,家居装修test.xls:
4:因子水平都不相同
根据2、3选择正交表,选择因子及水平略大于预估正交表,且实验次数最少的正交表即可。
* 在测试过程中,根据正交表得出来的结果,还需要人工添加
❸附录:
备注:欲卸载再次点击安装文件即可。
备注:使用英文冒号、英文逗号。

在Mac上使用
plain
brew install pict
export HOMEBREW_NO_INSTALL_CLEANUP=TRUE
brew install pict
cd pict
make
cp pict /usr/local/bin
cd Desktop
pict test.txt>test.xls
