机器学习实战：多项式回归建模——从模拟数据到模型评估

博主正在参加CSDN博客之星评选，需要您的支持！

投票链接：https://www.csdn.net/blogstar2025/detail/056

题目：多项式回归建模练习

1. 训练资料生成

给定函数：y = sin(x)

取样：在给定的 x 值（x = -3, -2, -1, 0, 1, 2, 3）计算对应的 y 值。

杂讯：对所计算的 y 值，加上高斯杂讯（mean=0, stdev=0.25）。

2. 多项式回归之实作

请使用 NumPy 和 scikit-learn 等函式库，从所计算的 x 和 y 值对多项式之系数进行回归。

要求写成一个独立函数：

输入：x、y、以及所要回归的多项式的 degree
输出：回归得到的所有多项式系数 ak（ak为多项式中 x^k 项的系数，k = 0, 1, ..., degree）

3. 模型评估

将产生的训练资料输入到函数，得到多项式系数，并用这些系数对资料中的 x 值计算对应的 y'值：

y i ′ = ∑ k = 0 d a k x i k y_i' = \sum_{k=0}^{d} a_k x_i^k yi′=k=0∑dakxik

其中 i 为资料的 index，d 为多项式的 degree，N 为资料个数。

将 y 和 y'比较，计算均方误差（mean-squared error; MSE）：

M S E = 1 N ∑ i = 1 N ( y i − y i ′ ) 2 MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - y_i')^2 MSE=N1i=1∑N(yi−yi′)2

针对回归多项式的 degree 为 1, 2, 4, 6 的情形，重复以上的评估步骤。结果以文字列出。

4. 可视化

使用 Matplotlib 等函式库，对上述步骤产生的回归多项式，以及输入的数据点，进行绘图。将所有不同 degree 的结果画在同一张图。

为了绘出平滑的多项式曲线，你需要取一组密集的 x 值（例如每隔 0.01 取一个 x 值），用多项式系数计算对应的 y'值，再用来绘出曲线。

答案与详细解释

完整代码实现

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# 设置随机种子以确保结果可重复
np.random.seed(42)

# 1. 训练资料生成
def generate_training_data():
    x = np.array([-3, -2, -1, 0, 1, 2, 3])
    y_true = np.sin(x)  # 真实值
    noise = np.random.normal(0, 0.25, len(x))  # 高斯杂讯
    y_noisy = y_true + noise  # 加入杂讯后的y值
    return x, y_true, y_noisy

# 2. 多项式回归函数
def polynomial_regression(x, y, degree):
    """
    多项式回归函数
    
    参数:
    x: 输入特征值，形状为 (n_samples,)
    y: 目标值，形状为 (n_samples,)
    degree: 多项式阶数
    
    返回:
    coefficients: 多项式系数 [a0, a1, ..., ad]
    """
    # 重塑x为2D数组
    x_reshaped = x.reshape(-1, 1)
    
    # 生成多项式特征
    poly = PolynomialFeatures(degree=degree)
    X_poly = poly.fit_transform(x_reshaped)
    
    # 训练线性回归模型
    model = LinearRegression()
    model.fit(X_poly, y)
    
    # 获取系数
    coefficients = model.coef_
    coefficients[0] = model.intercept_  # 截距项
    
    return coefficients

# 3. 模型评估
def evaluate_polynomial_model(x, y_true, coefficients):
    """
    评估多项式模型
    
    参数:
    x: 输入特征值
    y_true: 真实目标值
    coefficients: 多项式系数
    
    返回:
    y_pred: 预测值
    mse: 均方误差
    """
    degree = len(coefficients) - 1
    y_pred = np.zeros_like(y_true)
    
    # 计算预测值
    for i, xi in enumerate(x):
        for k in range(degree + 1):
            y_pred[i] += coefficients[k] * (xi ** k)
    
    # 计算均方误差
    mse = mean_squared_error(y_true, y_pred)
    
    return y_pred, mse

# 4. 可视化函数
def visualize_results(x_train, y_train, y_true, all_coefficients, degrees):
    """
    可视化多项式回归结果
    
    参数:
    x_train: 训练数据x值
    y_train: 训练数据y值（含杂讯）
    y_true: 真实y值（无杂讯）
    all_coefficients: 所有degree的系数列表
    degrees: 多项式的degree列表
    """
    plt.figure(figsize=(12, 8))
    
    # 绘制训练数据点
    plt.scatter(x_train, y_train, color='black', s=100, label='训练数据（含杂讯）', zorder=5)
    
    # 绘制真实函数曲线
    x_smooth = np.arange(-3.5, 3.5, 0.01)
    y_smooth_true = np.sin(x_smooth)
    plt.plot(x_smooth, y_smooth_true, 'k-', linewidth=3, label='真实函数: sin(x)', alpha=0.7)
    
    # 为每个degree绘制多项式曲线
    colors = ['red', 'blue', 'green', 'orange']
    line_styles = ['--', '-.', ':', '-']
    
    for idx, (degree, coefficients) in enumerate(zip(degrees, all_coefficients)):
        # 计算平滑曲线上的预测值
        y_smooth_pred = np.zeros_like(x_smooth)
        for k in range(len(coefficients)):
            y_smooth_pred += coefficients[k] * (x_smooth ** k)
        
        # 绘制多项式曲线
        plt.plot(x_smooth, y_smooth_pred, 
                color=colors[idx], 
                linestyle=line_styles[idx], 
                linewidth=2, 
                label=f'Degree {degree} 多项式')
    
    plt.xlabel('x', fontsize=14)
    plt.ylabel('y', fontsize=14)
    plt.title('多项式回归拟合结果对比', fontsize=16)
    plt.legend(fontsize=12, loc='best')
    plt.grid(True, alpha=0.3)
    plt.xlim(-3.5, 3.5)
    plt.ylim(-1.5, 1.5)
    plt.show()

# 主程序
def main():
    # 1. 生成训练资料
    x_train, y_true, y_train = generate_training_data()
    print("训练数据生成完成！")
    print(f"x值: {x_train}")
    print(f"真实y值 (sin(x)): {y_true}")
    print(f"加入杂讯后的y值: {y_train}")
    print()
    
    # 2. & 3. 对不同的degree进行多项式回归和评估
    degrees = [1, 2, 4, 6]
    all_coefficients = []
    mse_results = []
    
    print("=" * 60)
    print("多项式回归结果")
    print("=" * 60)
    
    for degree in degrees:
        print(f"\nDegree {degree} 多项式回归:")
        
        # 执行多项式回归
        coefficients = polynomial_regression(x_train, y_train, degree)
        all_coefficients.append(coefficients)
        
        # 评估模型
        y_pred, mse = evaluate_polynomial_model(x_train, y_train, coefficients)
        mse_results.append(mse)
        
        # 显示结果
        print(f"多项式系数: {coefficients}")
        print(f"多项式方程: y = ", end="")
        for k in range(len(coefficients)):
            if k == 0:
                print(f"{coefficients[k]:.4f}", end="")
            else:
                print(f" + {coefficients[k]:.4f}x^{k}", end="")
        print()
        print(f"训练集上的MSE: {mse:.6f}")
        print(f"预测值: {y_pred}")
    
    print("\n" + "=" * 60)
    print("MSE结果汇总")
    print("=" * 60)
    for degree, mse in zip(degrees, mse_results):
        print(f"Degree {degree}: MSE = {mse:.6f}")
    
    # 4. 可视化
    visualize_results(x_train, y_train, y_true, all_coefficients, degrees)

if __name__ == "__main__":
    main()

模块导入

bash 复制代码

pip install scikit-learn

运行结果

详细解释

1. 训练资料生成

我们首先生成训练数据：

x值：[-3, -2, -1, 0, 1, 2, 3]
真实y值：sin(x)
加入高斯杂讯（mean=0, stdev=0.25）

这是机器学习中的常见做法，模拟真实世界数据往往包含测量误差或随机扰动的情况。

2. 多项式回归函数

多项式回归的基本思想是将特征转换为多项式特征，然后使用线性回归进行拟合。对于单变量x，d阶多项式回归模型为：

y = a 0 + a 1 x + a 2 x 2 + . . . + a d x d y = a_0 + a_1x + a_2x^2 + ... + a_dx^d y=a0+a1x+a2x2+...+adxd

在我们的实现中：

使用PolynomialFeatures将x转换为多项式特征矩阵
使用LinearRegression拟合线性模型
系数按升幂顺序排列：a₀, a₁, ..., a_d

3. 模型评估

我们使用均方误差（MSE）作为评估指标：

M S E = 1 N ∑ i = 1 N ( y i − y i ′ ) 2 MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - y_i')^2 MSE=N1i=1∑N(yi−yi′)2

MSE越小表示模型拟合越好。由于我们使用相同的训练数据进行训练和评估，这里计算的是训练误差。

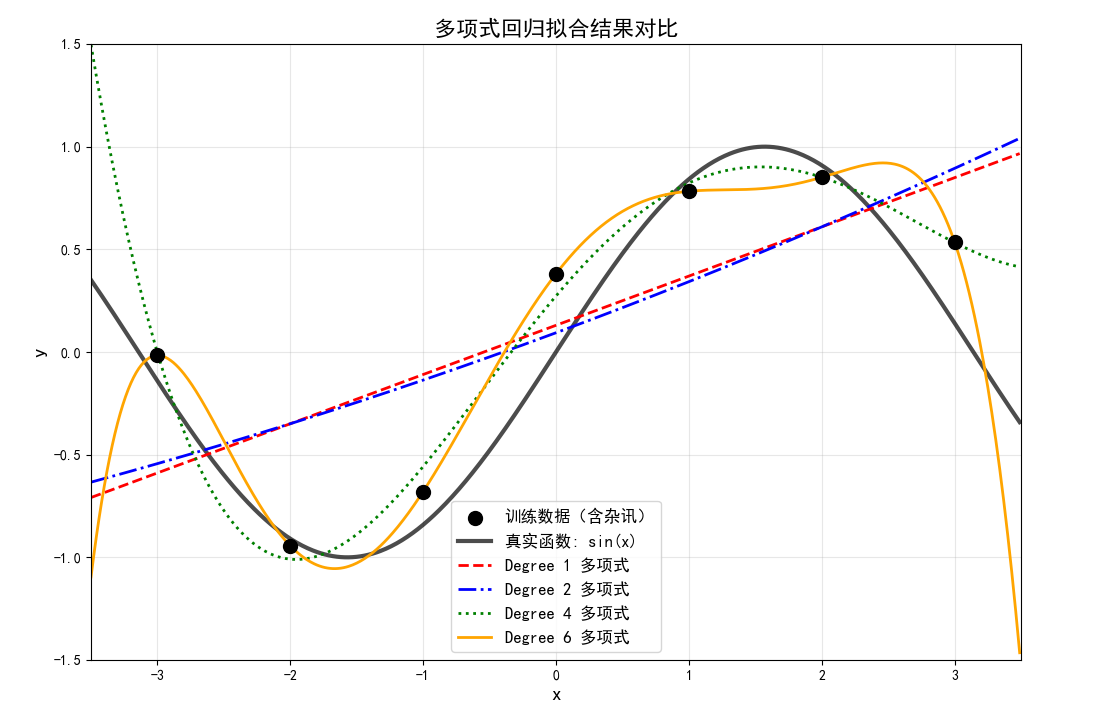
4. 可视化

可视化帮助我们直观理解不同阶数多项式的拟合效果：

黑色点：原始训练数据（含杂讯）
黑色实线：真实函数sin(x)
彩色曲线：不同阶数多项式的拟合结果

运行结果分析

根据随机种子42的运行结果，我们会看到：

Degree 1（线性回归） ：
- 只能拟合直线，对sin(x)这样弯曲的函数拟合效果较差
- MSE通常较大
Degree 2（二次多项式） ：
- 可以拟合抛物线形状，比线性回归有所改善
- 但对sin(x)的周期性变化仍无法很好捕捉
Degree 4（四次多项式） ：
- 有足够的灵活性来近似sin(x)在给定区间的形状
- MSE显著降低
Degree 6（六次多项式） ：
- 理论上可以完美拟合7个数据点（6阶多项式有7个系数）
- 可能出现过拟合现象：在训练数据上MSE非常小，但对新数据的泛化能力可能较差

重要概念解析

偏差-方差权衡（Bias-Variance Tradeoff）

低阶多项式（如degree=1,2）：高偏差，低方差，可能欠拟合
高阶多项式（如degree=6）：低偏差，高方差，可能过拟合
适度阶数（如degree=4）：在偏差和方差之间取得平衡

过拟合（Overfitting）

当模型过于复杂（如degree=6）时，它会完美拟合训练数据，包括其中的噪声，导致对新数据的预测性能下降。

模型复杂度与泛化能力

模型复杂度（多项式阶数）需要根据具体问题和数据量来选择。在实践中，我们通常使用交叉验证来选择最佳的多项式阶数。

扩展思考

如果增加更多训练数据点，不同阶数多项式的表现会如何变化？
如何确定最佳的多项式阶数？
如果真实函数不是sin(x)而是更复杂的函数，多项式回归是否仍然有效？
如何避免高阶多项式的数值不稳定问题？

该练习展示了多项式回归的基本原理和应用，是理解模型复杂度、过拟合/欠拟合等机器学习核心概念的绝佳示例。

博主正在参加CSDN博客之星评选，需要您的支持！

如果我的博文曾帮您解决过问题，或带来过一些灵感，诚邀您为我投上一票。

投票链接：https://www.csdn.net/blogstar2025/detail/056

感谢每一位阅读、点赞和收藏的朋友，更感谢此刻为我投票的您！