五道单链表练习题,都不算特别简单,有一些也需要思考好一会才想得过来。
一.单链表就地逆置 ★★★☆☆
题目
试写一算法,对单链表实现就地逆置,注意时间复杂度最好能达到O(n)
思路1
从尾结点开始找每个结点的前驱,然后使每个结点的后继为其前驱
代码1
cpp
void ReverseList(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return;
}
//找到尾结点,并记录
Node* p = plist;
while (p->next != NULL) {
p = p->next;
}
Node* q = p;
Node* d;
while (true) {
//找到q的前驱
d = plist;
while (d->next != q) {
d = d->next;
}
//q的前驱不是头结点,即q不是第一个结点
if (d != plist) {
//使q的后继为d
q->next = d;
//使q指向d
q = d;
}
else {
//q是第一个结点
//使其后继为NULL
q->next = NULL;
//使头结点后继为尾结点
d->next = p;
//退出循环,实现逆置
break;
}
}
}错误原因
实现了就地逆置(空间复杂度为O(1)),但是时间复杂度为O(n²)
思路2
使用一个Node*类型的数组保存下每个结点的地址,然后遍历链表,改变每个结点的后继
代码2
cpp
bool ReverseList(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//求出链表有效数据长度
int len = GetLength(plist);
//创建一个Node*类型的数组,保存各个结点的地址
Node** p = (Node**)malloc(sizeof(Node*) * len);
assert(p != NULL);
if (p == NULL) {
return false;
}
//遍历链表,使p保存各个结点的地址
Node* q = plist;
for (int i = 0; i < len; i++) {
p[i] = q->next;
q = q->next;
}
//改变每个结点的next
q = plist;
for (int i = len - 1; i >= 0; i--) {
q->next = p[i];
q = q->next;
}
free(p);
return true;
}错误原因
没有对尾结点进行处理,导致链表成环,同时虽然时间复杂度满足了O(n),但不符合就地逆置
在free(p); 前加上 q->next=NULL,使得尾结点后继为NULL,修正链表为环问题
同时在free(p); 后面加上 p=NULL; ++将野指针置空,提高安全性++
思路3
使用三个指针p、q、d记录连续的三个结点,一开始,p表示头结点,q表示第一个结点,d表示第二个结点,使q的后继为NULL,然后遍历链表,将三个指针向后移动,每次都将q的后继改为p,实现逆置,当d为尾结点时结束遍历,使头结点后继为d,d的后继为q,实现整个链表的逆置。
代码3
cpp
bool ReverseList(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//利用三指针记录连续的三个结点
Node* p = plist;
Node* q = p->next;
Node* d = q->next;
//使第一个结点的后继为NULL
q->next = NULL;
//遍历链表
while (d->next != NULL) {
//三个指针向后移动
p = q;
q = d;
d = d->next;
//使结点后继指向前驱
q->next = p;
}
//当d为尾结点时结束循环
//头结点后继改为尾结点
plist->next = d;
//尾结点后继指向前驱
d->next = q;
return true;
}错误原因
为对空链表/单结点链表进行判断处理,会导致代码直接崩溃
修改
cpp
bool ReverseList(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//利用三指针记录连续的三个结点
Node* prio = NULL;
Node* cur = plist->next;
Node* next = NULL;
//特殊情况的处理:
//1.当链表为空时不执行循环
//2.单结点链表时,头结点和第一个结点的后继不变
while (cur != NULL) {
next = cur->next;
cur->next = prio;
prio = cur;
cur = next;
}
//循环结束后,prio为尾结点,使头结点后继为prio,实现逆置
plist->next = prio;
return true;
}复杂度
N为单链表有效数据长度
时间复杂度:O(N)
空间复杂度:O(1)
思路4:"头插"法------重要
头插法是指链表的一种插入方法,每次需要插入一个新的元素,将其插入到头结点后,时间复杂度为O(1),通过头插法插入的元素,在链表中存储顺序跟插入顺序刚好想法,类似于逆置,所以可以采用类似于"头插"的方法实现链表的逆置。
使用"头插法"的大概思路:将单链表分为头结点部分和待逆置部分(除去头结点外的其它结点),记录待逆置部分的第一和第二个结点,然后将头结点的next置为NULL,使其称为空链表,然后将待逆置部分的结点依次用头插法插入到链表中。
代码
cpp
bool ReverseList(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
if (plist->next == NULL) {
printf("链表为空\n");
return true;
}
Node* p = plist->next;
if (p->next == NULL) {
return true;
}
Node* q = p->next;
//将链表变为空链表
plist->next = NULL;
//不断头插
while (p != NULL) {
q = q->next;
//绑线,先帮后面
p->next = plist->next;
//再绑前面
plist->next = p;
p = q;//p始终保存即将 头插 的结点
}
return true;
}复杂度
N为单链表有效数据长度
时间复杂度:O(N)
空间复杂度:O(1)
运行测试
测试代码
cpp
#include<stdio.h>
#include"list.h"
int main() {
Node list;
InitList(&list);
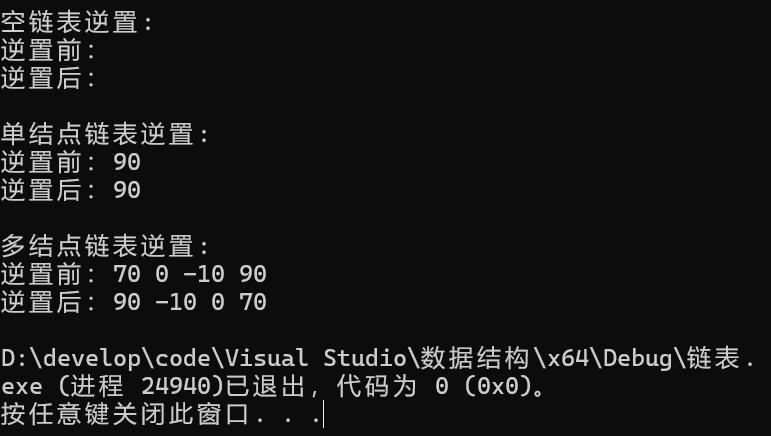
printf("空链表逆置:\n");
printf("逆置前:");
Show(&list);
ReverseList(&list);
printf("逆置后:");
Show(&list);
printf("\n单结点链表逆置:\n");
Insert_head(&list, 90);
printf("逆置前:");
Show(&list);
ReverseList(&list);
printf("逆置后:");
Show(&list);
printf("\n多结点链表逆置:\n");
Insert_head(&list, -10);
Insert_head(&list, 0);
Insert_head(&list, 70);
printf("逆置前:");
Show(&list);
ReverseList(&list);
printf("逆置后:");
Show(&list);
Destory(&list);
return 0;
}截图
二.删除倒数第k个结点 ★☆☆☆☆
题目
给定单链表头结点,删除链表中倒数第k个结点
思路1
倒数第k个结点,就是正数第 len-k+1 个结点。从前往后遍历链表到第 len-k 个结点,即第 len-k+1 个结点的前驱,记为p,q表示倒数第k个结点,使p->next=q->next,然后释放结点q即可
代码1
cpp
//删除倒数第k个结点
bool deleteKNode(List plist,int k) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
int len = GetLength(plist);
//对k进行判断
if (k <= 0 || k > len) {
printf("不存在倒数第%d个结点\n",k);
return false;
}
//找到倒数第k个结点的前驱
Node* p = plist;
for (int i = 0; i < len - k; i++) {
p = p->next;
}
//保存倒数第k个结点
Node* q = p->next;
p->next = q->next;
//释放
free(q);
q = NULL;//防止野指针
return true;
}错误原因
对空链表的处理不清晰,单独处理空链表:提示信息更精准,便于快速定位问题;能减少不必要的性能开销,更高效;代码逻辑更清晰,可读性更强
修正
单独增加对空链表的处理
cpp
//删除倒数第k个结点
bool deleteKNode(List plist,int k) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表直接返回
if (plist->next == NULL) {
printf("链表为空,删除失败\n");
return false;
}
int len = GetLength(plist);
//对k进行判断
if (k <= 0 || k > len) {
printf("不存在倒数第%d个结点\n",k);
return false;
}
//找到倒数第k个结点的前驱
Node* p = plist;
for (int i = 0; i < len - k; i++) {
p = p->next;
}
//保存倒数第k个结点
Node* q = p->next;
p->next = q->next;
//释放
free(q);
q = NULL;//防止野指针
return true;
}复杂度
N为链表有效数据个数
时间复杂度:O(N)。求长度函数将链表遍历一次、找前驱遍历一次,所以最坏情况下的时间复杂度为O(N)+O(N)=O(N)
空间复杂度:O(1)。
思路2
两个指针p、q,p先走k步,然后两个指针一起走,最后当p走到尾结点时,q指针所在的结点就是倒数第k个结点的前驱,然后按照链表的套路删除倒数第k个结点即可
代码
cpp
bool deleteKNode(List plist, int k) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表直接返回
if (plist->next == NULL) {
printf("链表为空,删除失败\n");
return false;
}
//对k进行判断
if (k <= 0) {
printf("不存在倒数第%d个结点\n",k);
return false;
}
Node* p = plist;
Node* q = plist;
//p先走k步
for (int i = 0; i < k; i++) {
//没走到k步就到了尾结点 → k>链表长度
if (p->next == NULL) {
return false;
}
p = p->next;
}
//同时向后移动
while (p->next != NULL) {
p = p->next;
q = q->next;
}
//保存结点
Node* r = q->next;
q->next = r->next;
//释放结点
free(r);
r = NULL;
return true;
}复杂度
n为链表有效结点个数
时间复杂度:O(n)。虽然有两个指针遍历链表,但遍历属于同一级,其中p指针的时间复杂度为O(n),q指针遍历的时间复杂度为O(m),m=n-k,所以总的时间复杂度为O(n)
空间复杂度:O(1)。
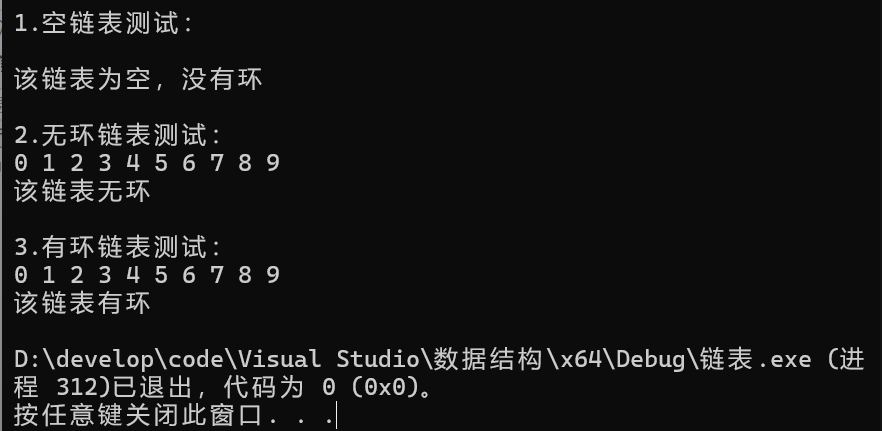
三.监测是否有环 ★★☆☆☆
题目
给定单链表,监测是否有环
思路1:哈希表
遍历链表的结点,利用哈希表存储遍历到的结点,当遍历到的结点已存在与哈希表中时,说明该链表有环,反之无环。遍历次数最多为链表结点数+1。
代码
cpp
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//创建哈希表,记录每个结点
//遍历链表,有环会再次遍历到哈希表中已有的结点
int len = GetLength(plist) + 1;//包括头结点也要记录到哈希表中
unordered_set<Node*> set(len);
Node* p = plist;
for (int i = 0; i < len + 1; i++) {
//没有环,遍历到链表之外了
if (p == NULL) {
return false;
}
//哈希表中没有遍历到的结点
if (set.find(p) == set.end()) {
set.insert(p);//将该结点放入哈希表
p = p->next;//移动结点
continue;//继续遍历
}
//遍历到的结点已在哈希表中,说明有环
return true;
}
//遍历完了还没有遇到环,说明没有环,返回false
return false;
}错误2
测试函数
错误原因
1.GetLength(plist)在有环链表场景下会陷入死循环:因为GetLength函数的循环遍历链表时,循环结束条件是 p==NULL,在手动添加环后,p==NULL不能发生,所以陷入死循环
cpp
//获取长度
int GetLength(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return -1;
}
Node* p = plist->next;
int count = 0;
while (p != NULL) {
count++;
p = p->next;
}
return count;
}2.for (int i = 0; i < len; i++)的遍历次数被len限制,无法检测到环:即使GetLength函数没有问题,len的值也只是表示无环链表的结点个数,但是最坏情况下(首尾结点连接成环),要找到环,即找到原来遍历过的结点,需要多遍历一次,所以for循环遍历次数错误
修正
抛弃GetLength求长度的逻辑,同时修改遍历逻辑:使用while循环,直到找到环或遍历到NULL
cpp
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//创建哈希表,记录每个结点
//遍历链表,有环会再次遍历到哈希表中已有的结点
unordered_set<Node*> set;
Node* p = plist;
//一直遍历链表,直到遍历完或遇到环
while (p != NULL) {
//在数组中查看是否已有该结点
bool flag = false;
for (int j = 0; j < set.size(); j++) {
if (set.find(p) != set.end()) {
flag = true;
break;
}
}
//数组中有该结点→有环
if (flag) {
return true;
}
//没有该结点,将其放入数组
set.insert(p);
//移动结点
p = p->next;
}
//遍历完了还没有遇到环,说明没有环,返回false
return false;
}优化
冗余逻辑(内层 for 循环) :代码中 for (int j = 0; j < set.size(); j++) 是完全冗余的 ------set.find(p) 本身已经完成了「查找结点是否存在」的逻辑,内层 for 循环只是重复执行 set.find(p)
cpp
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//创建哈希表,记录每个结点
//遍历链表,有环会再次遍历到哈希表中已有的结点
unordered_set<Node*> set;
Node* p = plist;
//一直遍历链表,直到遍历完或遇到环
while (p != NULL) {
//在数组中查看是否已有该结点
if (set.find(p) != set.end()) {
//数组中有该结点→有环
return true;
}
//没有该结点,将其放入数组
set.insert(p);
//移动结点
p = p->next;
}
//遍历完了还没有遇到环,说明没有环,返回false
return false;
}复杂度
N为链表结点个数
时间复杂度:O(N)
空间复杂度:O(N)
思路2:数组
将思路1的哈希表换为动态数组即可
代码
cpp
//2.利用数组保存已遍历结点
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//创建数组保存结点
vector<Node*> arr;
Node* p = plist;
//一直遍历链表,直到遍历完或遇到环
int i = 0;
while(p != NULL){
//在数组中查看是否已有该结点
bool flag = false;
for (int j = 0; j < arr.size(); j++) {
if (arr[j] == p) {
flag = true;
break;
}
}
//数组中有该结点→有环
if (flag) {
return true;
}
//没有该结点,将其放入数组
arr[i++] = p;
//移动结点
p = p->next;
}
return false;
}错误1
使用的测试代码
cpp
int main() {
Node list;
InitList(&list);
printf("1.空链表测试:\n");
Show(&list);
isHaveLoop(&list);
printf("2.无环链表测试:\n");
InitList(&list);
for (int i = 0; i < 10; i++)
{
Insert(&list, i, i);
}
Show(&list);
isHaveLoop(&list);
return 0;
}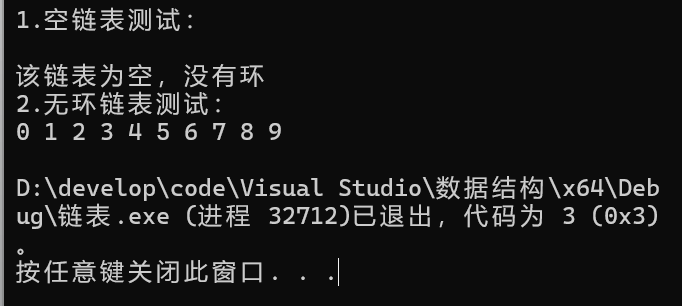
出现错误
无法处理无环的单链表

表示:试图访问一个 vector 中不存在的下标位置,也就是下标超出了 vector 当前的有效范围
修改
arr[i]访问越界,因为初始化时arr默认为空,所以长度为0,无法通过下标访问
需要换为arr.push_back()添加元素
cpp
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//创建数组保存结点
vector<Node*> arr;
Node* p = plist;
//一直遍历链表,直到遍历完或遇到环
while(p != NULL){
//在数组中查看是否已有该结点
bool flag = false;
for (int j = 0; j < arr.size(); j++) {
if (arr[j] == p) {
flag = true;
break;
}
}
//数组中有该结点→有环
if (flag) {
return true;
}
//没有该结点,将其放入数组
arr.push_back(p);
//移动结点
p = p->next;
}
return false;
}复杂度
n为链表结点个数
时间复杂度:O(n²)。嵌套循环:外层循环遍历每一次数组,内层循环每一次都需要遍历数组中已存储2的结点,所以总的时间复杂度为O(n)+O(0 + 1 + 2 + ... + (n-1))=O(n²)。
空间复杂度:O(n)。额外空间开销主要是数组arr的空间,最坏情况下,需要存储链表的所有结点,所以空间复杂度为O(n)。
思路3:快慢指针
使用两个指针,一快一慢,快指针fast每次移动到下下个结点,慢指针slow每次移动到下一个结点,如果链表没有环,那么最后肯定会出现fast->next==NULL或fast==NULl的情况,如果没环,fast肯定会和slow相遇。
代码
cpp
bool isHaveLoop(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return false;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return false;
}
//快慢指针
Node* slow = plist->next;
Node* fast = plist->next->next;
//链表被遍历完
while (fast != NULL && fast->next != NULL) {
//快慢指针相遇→有环
if (slow == fast) {
return true;
}
//慢指针每次走一步
slow = slow->next;
//快指针每次走两步
fast = fast->next->next;
}
//循环结束→无环
return false;
}复杂度
N为链表结点数
时间复杂度:O(N)。遍历次数与N成正比,所以时间复杂度就是O(N)。
空间复杂度:O(1)。仅使用了两个指针变量,指针变量的数量和占用的内存大小固定,不随链表结点数 n 变化,所以空间复杂度为O(1)。
四.相交链表 ★★☆☆☆
题目
给定两个单链表(head1,head2),检测两个链表是否有交点,如果有返回第一个交点地址
这道题在练题100天------DAY25:升序合并文件+相交链表+多数元素-CSDN博客中做过,当时使用了 哈希表 的方法,官方题解利用了 "使两个指针在链表上移动距离一样" 的思路,这里补充另外一个思路
思路
创建两个指针,分别遍历两个链表,但是如果两个链表有交点,想要使两个指针相遇,就需要使它们到交点的距离一致。因为交点后的长度一致,所以需要使交点前移动的距离一致,即可以使在较长的链表上的指针先移动一段距离,使得两个指针同时移动到交点的距离一致。
注意:如果两个链表没有交点,在两个交点相等时,表示两个指针移动到了尾结点的next,即NULL,所以++不能仅仅通过两个指针相等来判断是否有交点++
代码
cpp
Node* IsIntersected(Node* head1, Node* head2) {
assert(head1 != NULL && head2 != NULL);
if (head1 == NULL || head1 == NULL) {
return NULL;
}
//创建两个指针,分别遍历两个链表
//如果有交点,两个指针与交点距离一样,才能在交点相遇
//所以更长的一个链表的指针需要先移动一段距离
int len1 = GetLength(head1);//链表1的长度
int len2 = GetLength(head2);//链表2的长度
Node* p = head1;
Node* q = head2;
//移动指针,使两指针一起移动时移动距离一致
while (len1 > len2) {
p = p->next;
len1--;
}
while (len2 > len1) {
q = q->next;
len2--;
}
while (p != NULL && q != NULL) {
//相遇/相等时退出循环
if (p == q) {
break;
}
//一起移动
p = p->next;
q = q->next;
}
//在交点相遇
if (p == q && p != NULL) {
return p;
}
//一起移动到末尾,无交点
return NULL;
}复杂度
m、n分别为两个链表的长度
时间复杂度:O(m+n)。最坏情况:无交点以及交点在尾结点,都需要遍历完两个链表,所以总的时间复杂度为O(m+n)。
空间复杂度:O(1)。
五.求链表中环的第一个结点 ★★★☆☆
题目
给定单链表,如果有环,返回从头结点进入环的第一个结点
思路1:哈希表
利用判断链表中是否有环的思路,遇到哈希表中已有的结点,直接返回
代码
cpp
Node* FirstCircleNode(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return NULL;
}
//空链表判断
if (plist->next == NULL) {
printf("该链表为空,没有环\n");
return NULL;
}
//创建哈希表,记录每个结点
//遍历链表,有环会再次遍历到哈希表中已有的结点
unordered_set<Node*> set;
Node* p = plist;
//一直遍历链表,直到遍历完或遇到环
while (p != NULL) {
//在数组中查看是否已有该结点
if (set.find(p) != set.end()) {
//数组中有该结点→有环
return p;
}
//没有该结点,将其放入数组
set.insert(p);
//移动结点
p = p->next;
}
//遍历完了还没有遇到环,说明没有环,返回NULL
return NULL;
}复杂度
n为链表的结点数
时间复杂度:O(n)。外层循环,每个结点被遍历一次,总遍历次数为n;内层,哈希表操作(set.find(p) / set.insert(p))的平均时间复杂度为 O (1),所以总的时间复杂度为O(n)*O(1)=O(n)。
空间复杂度:O(n)。哈希表存储n个结点。
思路2 ★★★★☆
首先利用快慢指针判断该链表是否是环。
然后一指针从快慢指针相遇的位置开始,另一指针从头结点开始,同时移动,它们相遇的地方就是环的第一个结点。
这一结论的推导过程大致如下:
1.设头结点A到环的第一个结点B这段链表共有a个结点,从环的第一个结点B到快慢指针相遇的结点C这段链表共有b个结点,环共有c个结点
2.快指针每次移动两下,慢指针每次移动一下,它们同时开始移动,则可以得知:慢指针移动距离*2=快指针移动距离。慢指针移动距离为a+b,快指针移动距离为a+b+k*c,其中k为快指针绕环的圈数,则有2*(a+b)=a+b+k*c,化简得 a=k*c-b
3.由 a=k*c-b可以推得,如果一个指针 r 从头结点A出发,一个指针 p 从快慢指针相遇处C出发,在 p 指针在环上跑了(k-1)圈,由多跑了(c-b),即总路程为(k*c-b)个结点时,p指针跑到环的第一个结点B处,r指针跑的路程为a,也到了环的第一个结点B处,两指针相遇,由此可得出环的第一个结点地址。
代码
cpp
Node* FirstCircleNode(List plist) {
assert(plist != NULL);
if (plist == NULL) {
return NULL;
}
//空链表判断
if (plist->next == NULL) {
return NULL;
}
//快慢指针
Node* p = plist->next->next;
Node* q = plist->next;
while (p != NULL && p->next != NULL && p != q) {
p = p->next->next;
q = q->next;
}
//p和q没有相遇→没有环
if (p == NULL || p->next == NULL) {
return NULL;
}
//一指针从头结点出发
Node* r = plist;
//同时出发,最后会在环的第一个结点相遇
while (r != p) {
r = r->next;
p = p->next;
}
return r;
}复杂度
n为链表有效结点个数
时间复杂度:O(n)。两次线性遍历(找相遇点 + 找入口),总次数与链表结点数成正比。
空间复杂度:O(1)。仅使用 3 个指针变量,无额外动态内存开销。