---关注作者,送A/B实验实战工具包
做 AB 实验平台架构,最核心的挑战只有一个:流量是有限的,而实验需求是无限的。
如果一个 App 有 1 亿日活,听起来很多。但如果每个实验都要独占 10% 的流量,你最多只能同时跑 10 个实验。对于像字节、阿里、谷歌这样动辄上千个实验并发的大厂,这种"独占式"的玩法会让业务迭代速度直接停摆。
如何让同一个用户在同一时间身上背着几十个实验,且这些实验之间互不干扰?
这就涉及到了流量分发的底层架构:分层(Layering)与分域(Domain/Bucketing) 。基于此,衍生出了两种最基本的实验关系:正交(Orthogonal)与互斥(Mutually Exclusive)。
1. 流量架构的鼻祖:Google 重叠实验框架
早在 2010 年,Google 就发布了经典的论文 Overlapping Experiment Infrastructure,奠定了现代 AB 实验平台的工业标准。
在这个框架下,流量不再是一张平面的大饼,而是一个立体的多维空间。
- 分域 (Domain) :横向切分。
- 把流量像切蛋糕一样切开。
- 特点:硬隔离。在这个域里的流量,绝对不会跑到那个域去。
- 分层 (Layer) :纵向重叠。
- 把流量像千层饼一样叠起来。
- 特点:复用。同一个用户可以同时处于 UI 层、推荐层、广告层。
基于这个架构,我们定义了两种实验关系。
2. 核心概念解析
2.1 互斥实验 (Mutually Exclusive Experiments)
定义 :
在同一层 (Layer) 内,流量被切割成若干个不重叠的桶 (Bucket)。用户命中了一个桶,就绝对不可能命中另一个桶。
痛点解决 :
解决资源冲突 和逻辑冲突 。
如果两个实验都在修改同一个按钮的颜色,或者都在调整同一个广告位的计费逻辑,它们必须互斥。否则用户看到一个"又红又蓝"的按钮,或者系统出现逻辑死锁。
技术实现 :
使用相同 的哈希因子(Salt)。
Bucket ID=hash(uid+Layer_Salt)%100 \text{Bucket ID} = \text{hash}(\text{uid} + \text{Layer\_Salt}) \% 100 Bucket ID=hash(uid+Layer_Salt)%100
因为 Salt 相同,同一个 UID 算出来的 Bucket ID 是固定的,确保了互斥。
2.2 正交实验 (Orthogonal Experiments)
定义 :
在不同层 (Layer) 之间,流量是重新打散的。
用户在 A 层命中了实验 1,在 B 层命中实验 2 的概率是完全随机的。实验 1 的流量均匀地分布在实验 2 的各个组中。
痛点解决 :
解决流量利用率 问题。
通过正交,我们可以让 UI 实验、算法实验、底层架构实验并行跑在同一个用户身上,理论上可以将流量利用率提升 N 倍(N = 层数)。
技术实现 :
使用独立的哈希因子(Salt)。
- Layer A: \\text{hash}(\\text{uid} + \\text{Salt_A}) % 100
- Layer B: \\text{hash}(\\text{uid} + \\text{Salt_B}) % 100
由于 Salt 不同,Layer A 的分桶结果与 Layer B 的分桶结果在数学上是独立 的。
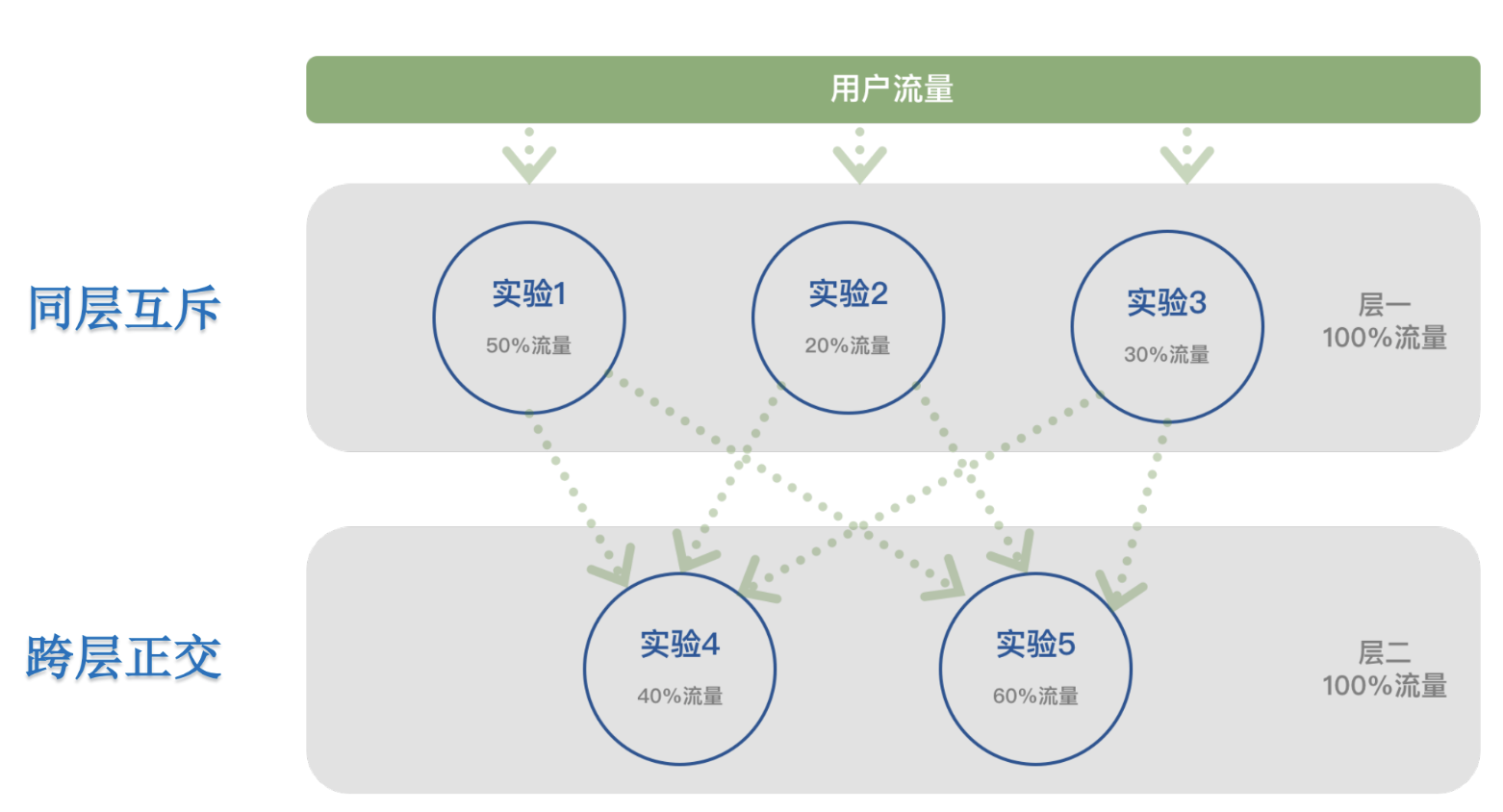
3. 实战推演:业务场景中的取舍
为了让你彻底理解,我们用两个具体的业务场景来推演。
场景一:电商 App 首页改版
背景:
- UI 团队想测试"购买按钮"是红色好还是蓝色好。
- 算法团队想测试"猜你喜欢"是用协同过滤(CF)还是深度学习(DeepFM)。
实验设计:
-
互斥关系:
- 如果 UI 团队还有一个方案是"绿色按钮"。那么"红 vs 蓝 vs 绿"这三个策略必须互斥。你不能让一个用户看到的按钮既是红的又是绿的。
- 它们共享"UI 层"的流量,比如各占 33%。
-
正交关系:
- UI 实验(红/蓝)和 算法实验(CF/DeepFM)应当正交。
- 为什么? 按钮颜色和推荐算法通常没有强耦合。
- 结果 :
- 用户 A:看到红按钮 + 推荐出的商品是 DeepFM 算的。
- 用户 B:看到红按钮 + 推荐出的商品是 CF 算的。
- 用户 C:看到蓝按钮 + 推荐出的商品是 DeepFM 算的。
- 好处:两个团队都不需要等待对方,都拥有 100% 的全量用户进行测试,效率最大化。
场景二:消息推送 (Push) 优化
背景:
- 文案团队想测试 Push 的标题:"惊爆价" vs "限时购"。
- 时机团队想测试 Push 的发送时间:早上 9 点 vs 晚上 8 点。
实验设计:
-
互斥关系:
- "惊爆价"和"限时购"必须互斥。同一个用户对同一条 Push 只能看到一个标题。
-
正交关系:
- 文案实验和发送时间实验应当正交。
- 结果 :
- 组 1:早上 9 点收到"惊爆价"。
- 组 2:早上 9 点收到"限时购"。
- 组 3:晚上 8 点收到"惊爆价"。
- 组 4:晚上 8 点收到"限时购"。
- 好处 :我们可以同时评估文案的影响和时间的影响。如果发现"晚上 8 点 + 限时购"效果最好,这就是正交实验带来的组合收益洞察。
4. 特殊形态:父子实验 (Parent-Child Experiments)
除了平行的正交和互斥,还有一种包含关系,称为父子实验。
概念 :
在父实验划定的流量范围内,再开启子实验。子实验的流量完全来自于父实验。
业务场景 :
假设你要对"收银台"进行一次重构(父实验),流量占比 10%。
在新的收银台页面里,你又想测试"是否默认勾选优惠券"(子实验)。
设计逻辑:
- 父层:全站流量切 10% 给"新收银台",90% 给"旧收银台"。
- 子层:在那 10% 的"新收银台"流量里,再切 50% 给"默认勾选",50% 给"不勾选"。
为什么这么设计(What & Why):
- 逻辑依赖:子实验(勾选优惠券)的代码逻辑只存在于新收银台中,旧收银台根本没这个功能。如果做成正交,旧收银台的用户命中"勾选实验"会报错或无任何效果。
- 风险隔离 :如果新收银台挂了,只需要关掉父实验,子实验自然也就停了。这是一种灰度发布 与精细化测试结合的高级手段。
如果这篇文章帮你理清了思路,不妨点个关注,我会持续分享 AB 实验干货文章。
