文章目录
概要
https://github.com/rllab-snu/Stage-Wise-CMORL
论文:"Stage-Wise Reward Shaping for Acrobatic Robots: A Constrained Multi-Objective Reinforcement Learning Approach".
这项研究提出了一种分阶段奖励塑型 方法,旨在简化机器人学习复杂特技动作的训练过程。研究人员利用受限多目标强化学习框架,将翻转、倒立行走等任务拆解为多个逻辑阶段 ,并为每个阶段独立定义奖励与成本函数 。为了优化策略,该团队开发了名为 CoMOPPO 的新算法,能够同时兼顾多个动作目标并严格遵守安全约束。

想象一下,我们要教一个四足机器人完成一个漂亮的后空翻。这是一个极其复杂的任务,远非简单的"前进"或"后退"指令可比。在传统的强化学习(RL)中,我们通常需要设计一个单一的、包罗万象的奖励函数,它必须同时考虑任务表现(比如跳跃高度)、安全性(比如身体不能碰撞地面)和能效(比如关节扭矩不能太大)等所有因素。
当任务涉及到像后空翻这样"一系列复杂动作 "时,难题会进一步加剧。在动作的初始阶段,我们希望机器人专注于准备和起跳;而在空中和落地阶段,关注的重点则会转移到身体姿态控制和稳定着陆上。这意味着在'起跳 (Jump)'阶段,我们希望奖励机器人以获得最大的向后角速度(base velocity 奖励 −ωy),但在'落地 (Land)'阶段,我们又希望奖励它保持静止(base velocity 奖励 −(v²x + v²y + ω²z))。手动设计一个平滑切换这些目标的单一函数极其困难。
为了解决这一挑战,研究人员提出了分阶段约束多目标强化学习 (Stage-Wise Constrained Multi-Objective Reinforcement Learning, CMORL)框架。该框架的核心思想十分巧妙:它不再试图用一个复杂的函数来解决所有问题,而是将一个复杂的特技动作分解为多个逻辑阶段,并为每个阶段独立定义需要实现的目标(奖励)和需要遵守的规则(成本),从而极大地简化了奖励设计过程。

- 提出一种基于 CMORL 框架的新型奖励塑形过程,以分阶段方式定义多个奖励与成本函数;
- 引入一种实用的 CMORL 算法:通过适配 PPO 以处理多目标与约束;
- 所提方法已在仿真与真实环境中成功完成多种杂技任务。
背景知识
约束多目标强化学习
多目标 RL(MORL)分为两类:
- 单策略方法[17,18]:旨在找到一个帕累托最优策略;
- 多策略方法[19-23]:旨在找到一组覆盖帕累托前沿的策略。
单策略方法通过效用函数 [24] 或偏好向量 [17,18] 将多目标转化为单目标 ,从而适配现有 RL 算法进行策略更新。多策略方法则通过并行更新多策略以适配不同偏好 [20,22],或训练一个基于偏好的通用策略以表示多种策略 [19,23]。
其中,LP3 [25] 与 CoMOGA [14] 是扩展现有 MORL 算法的 CMORL 算法,分别采用拉格朗日 [26] 与原始 [27] 方法处理约束。所提算法 CoMOPPO 可视为简化 CoMOGA 实现的单策略方法。
约束多目标马尔可夫决策过程
约束多目标马尔可夫决策过程(CMOMDP)定义为元组 ( S , A , P , ρ , γ , R 1 : N , C 1 : M ) (S, A, P, \rho, \gamma, R_{1:N}, C_{1:M}) (S,A,P,ρ,γ,R1:N,C1:M),其中:S:状态空间;A:动作空间;P:状态转移概率; ρ \rho ρ:初始状态分布; γ \gamma γ:折扣因子; R 1 : N R_{1:N} R1:N:N个奖励函数; C 1 : M C_{1:M} C1:M:M个成本函数。
策略定义为 π : S → P ( A ) \pi: S \to \mathcal{P}(A) π:S→P(A)( π ( s ) \pi(s) π(s)表示状态s下执行动作的概率)。轨迹定义为 τ = { s 0 , a 0 , s 1 , a 1 , ... } \tau = \{s_0, a_0, s_1, a_1, \dots\} τ={s0,a0,s1,a1,...},其中 s 0 ∼ ρ s_0 \sim \rho s0∼ρ、 a t ∼ π ( ⋅ ∣ s t ) a_t \sim \pi(\cdot|s_t) at∼π(⋅∣st)、 s t + 1 ∼ P ( ⋅ ∣ s t , a t ) s_{t+1} \sim P(\cdot|s_t, a_t) st+1∼P(⋅∣st,at)。
动作价值函数定义为: Q R π ( s , a ) : = E τ ∼ π [ ∑ t = 0 ∞ γ t R ( s t , a t , s t + 1 ) ] , Q_R^\pi(s,a) := \mathbb{E}{\tau \sim \pi}\left[ \sum{t=0}^\infty \gamma^t R(s_t, a_t, s_{t+1}) \right], QRπ(s,a):=Eτ∼π[t=0∑∞γtR(st,at,st+1)],其中 s 0 = s s_0 = s s0=s、 a 0 = a a_0 = a a0=a。状态价值函数为 V R π ( s ) : = E a ∼ π ( ⋅ ∣ s ) [ Q R π ( s , a ) ] V_R^\pi(s) := \mathbb{E}_{a \sim \pi(\cdot|s)}[Q_R^\pi(s,a)] VRπ(s):=Ea∼π(⋅∣s)[QRπ(s,a)],优势函数为 A R π ( s , a ) : = Q R π ( s , a ) − V R π ( s ) A_R^\pi(s,a) := Q_R^\pi(s,a) - V_R^\pi(s) ARπ(s,a):=QRπ(s,a)−VRπ(s)。
成本函数的价值与优势函数定义方式与奖励函数一致,只需将 R i R_i Ri替换为 C j C_j Cj即可。在 CMORL 问题中,奖励函数用于构建目标,成本函数用于构建约束。
CMORL 问题设定
CMORL 问题定义如下: max π J R i ( π ) ∀ i ∈ { 1 , ... , N } s.t. J C j ( π ) ≤ d j / ( 1 − γ ) ∀ j ∈ { 1 , ... , M } , (1) \begin{aligned} &\max_{\pi} J_{R_i}(\pi) \quad \forall i \in \{1,\dots,N\} \\ &\text{s.t. } J_{C_j}(\pi) \leq d_j/(1-\gamma) \quad \forall j \in \{1,\dots,M\}, \end{aligned} \tag{1} πmaxJRi(π)∀i∈{1,...,N}s.t. JCj(π)≤dj/(1−γ)∀j∈{1,...,M},(1)其中 J R i ( π ) : = E τ ∼ π [ ∑ t = 0 ∞ γ t R i ( s t , a t , s t + 1 ) ] J_{R_i}(\pi) := \mathbb{E}{\tau \sim \pi}\left[ \sum{t=0}^\infty \gamma^t R_i(s_t, a_t, s_{t+1}) \right] JRi(π):=Eτ∼π[∑t=0∞γtRi(st,at,st+1)], d j d_j dj是第j个约束的阈值。CMORL 问题的目标是找到约束帕累托(CP)最优策略[14]。
给定两个可行策略 π 1 , π 2 ∈ { π ∣ J C j ( π ) ≤ d j / ( 1 − γ ) ∀ j } \pi_1, \pi_2 \in \{\pi|J_{C_j}(\pi) \leq d_j/(1-\gamma) \ \forall j\} π1,π2∈{π∣JCj(π)≤dj/(1−γ) ∀j},若对所有i满足 J R i ( π 1 ) ≤ J R i ( π 2 ) J_{R_i}(\pi_1) \leq J_{R_i}(\pi_2) JRi(π1)≤JRi(π2),则称 π 1 \pi_1 π1被 π 2 \pi_2 π2支配。若一个策略不被任何其他策略支配,则该策略是 CP 最优的。
由于 CP 最优策略不唯一,可通过偏好向量 ω ∈ Ω = { v ∈ R N ∣ ∑ v i = 1 , v i ≥ 0 } \omega \in \Omega = \{v \in \mathbb{R}^N | \sum v_i = 1, v_i \geq 0\} ω∈Ω={v∈RN∣∑vi=1,vi≥0}将多目标转化为单目标,从而得到特定策略。这种转化可通过线性加权 [23,24] 或其他标量化方法 [17,18] 实现,随后即可应用单目标 RL 算法获取策略。
所提方法
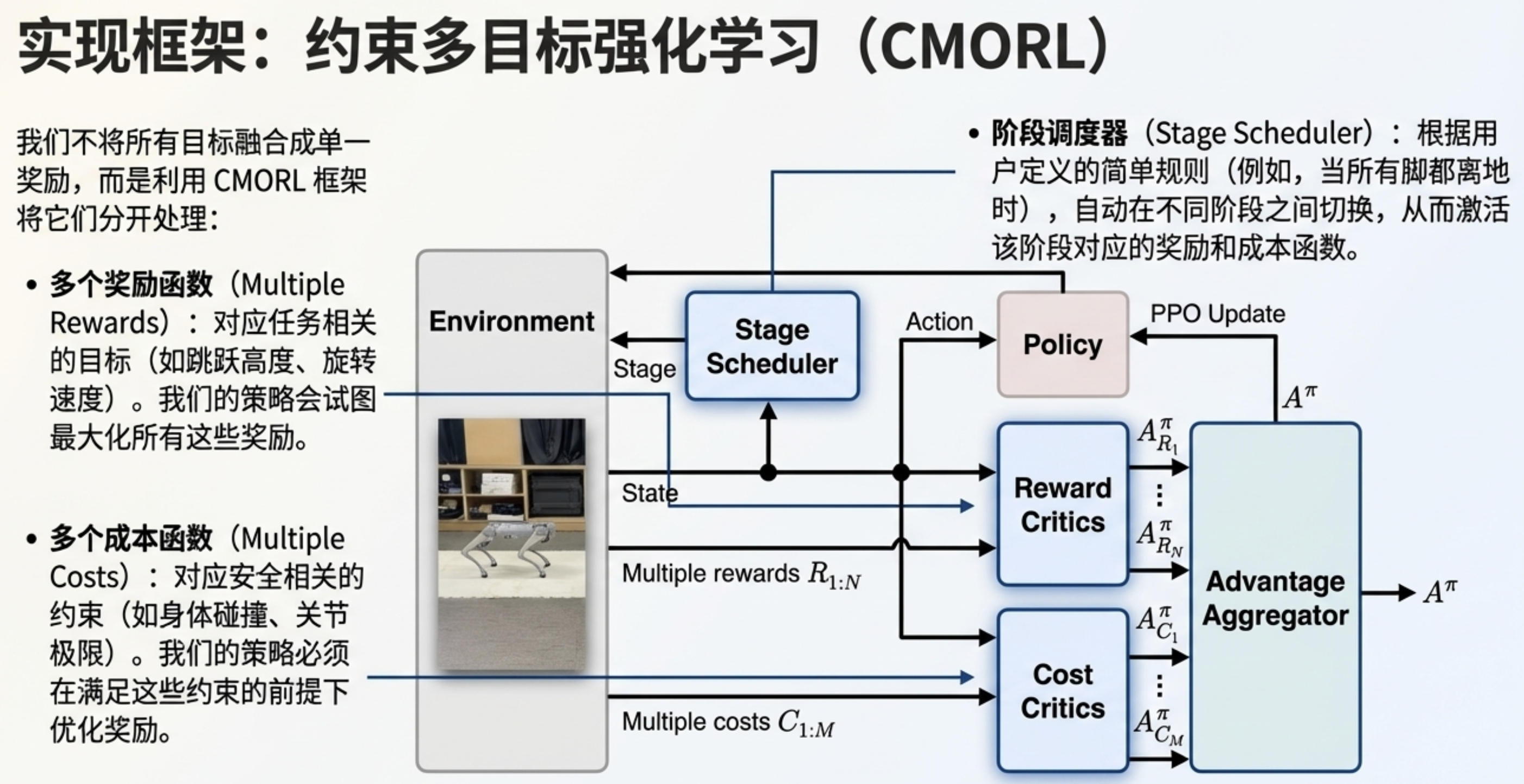
分阶段奖励塑形
通常,奖励函数包含多个项(任务相关项、正则化项、安全相关项)。我们不将所有项整合为单一标量奖励,而是采用 CMORL 框架:最大化与每个奖励项对应的多目标,同时满足与安全相关项对应的约束。
此外,对于需要连续动作的复杂任务,动态调整各奖励项的权重会进一步增加奖励塑形的难度。为解决这一问题,我们提出将任务划分为一系列阶段,并以分阶段的方式定义奖励与成本函数。
将任务分段可明确每个阶段所需的动作,从而简化奖励塑形过程。
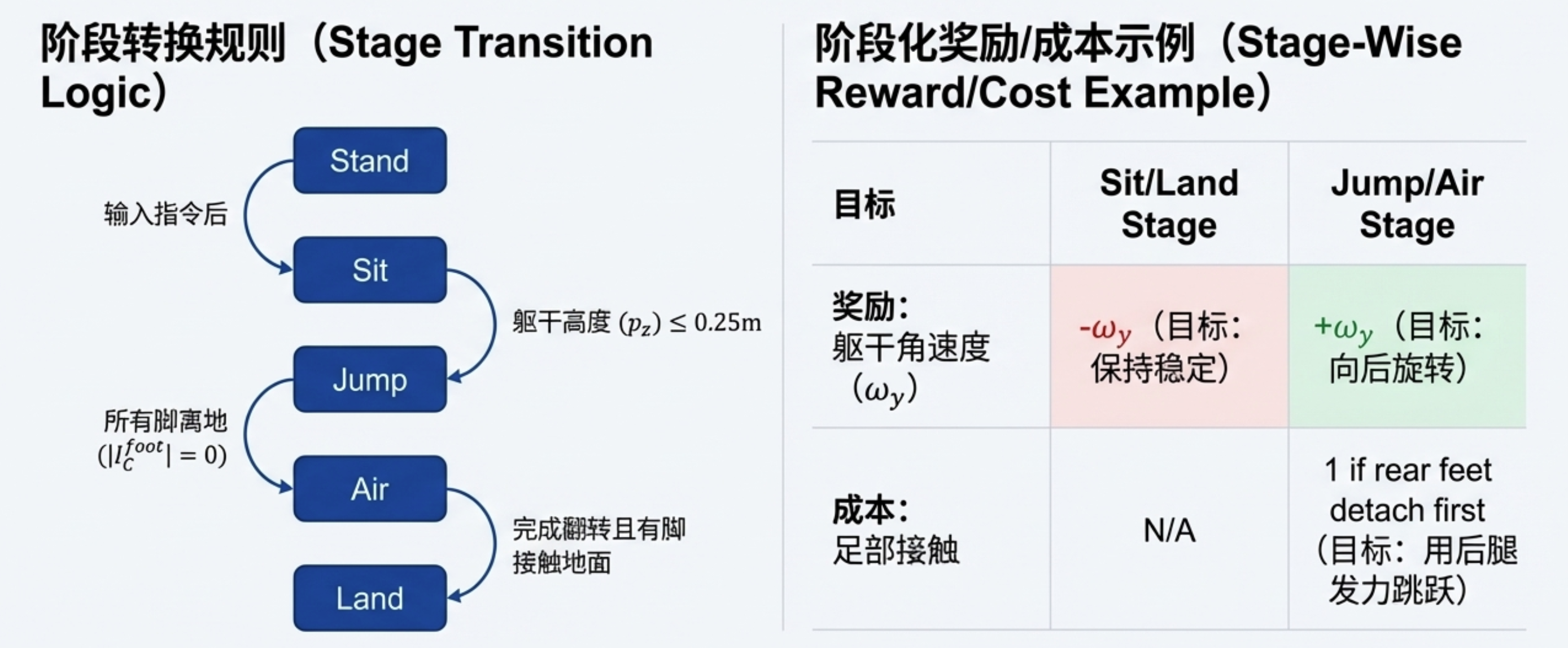
以该示例为例,我们将介绍阶段的划分方式及奖励 / 成本函数的定义方法。
阶段转换:
完成后空翻任务的机器人需在接收到指令前保持待机状态;接收到指令后,机器人先小幅坐下,随后跳跃并在空中旋转,最终落地。基于这一流程,任务可划分为 5 个阶段:"待机(Stand)- 坐下(Sit)- 跳跃(Jump)- 空中(Air)- 落地(Land)"。
奖励与成本函数:
在 "待机" 与 "坐下" 阶段,机器人需保持静止,因此基础速度奖励定义为当前速度的负值;反之,在 "跳跃" 与 "空中" 阶段,机器人需向后旋转,因此速度奖励被设置为y方向角速度。同时,为确保这些阶段中足够的跳跃高度,高度奖励被设置为基础高度。
为防止 "跳跃" 与 "空中" 阶段发生倾斜,平衡奖励被设置为基础的y轴与世界坐标系z轴之间的角度;在其他阶段,奖励被设置为最小化基础z轴与世界坐标系之间的角度,以保持机器人直立。
能量与样式奖励用作正则化项,以确保自然动作;身体接触成本用于防止机器人摔倒;关节位置、速度、扭矩相关的成本用于将这些值限制在合理范围内;足部接触成本是专为后腿跳跃设计的项:若后腿先于前腿离地,则会触发该成本。
CMORL 策略更新
引入一种策略更新规则(名为约束多目标 PPO(CoMOPPO)),旨在最大化多目标的同时满足约束 。根据 Kim 等人 [14] 的研究,通过加权求和的方式聚合奖励与成本的优势函数 (权重需满足特定条件),并使用 TRPO [33] 结合聚合后的优势函数更新策略,可收敛到 CP 最优策略。其形式如下: π t + 1 = arg max π E τ ∼ π t [ π ( a ∣ s ) π t ( a ∣ s ) A π t ( s , a ) ] s.t. E τ ∼ π t [ D KL ( π ( ⋅ ∣ s ) ∥ π ( ⋅ ∣ s ) ) ] ≤ ϵ , (2) \begin{aligned} \pi_{t+1} &= \argmax_{\pi} \mathbb{E}{\tau \sim \pi_t} \left[ \frac{\pi(a|s)}{\pi_t(a|s)} A^{\pi_t}(s,a) \right] \\ &\text{s.t. } \mathbb{E}{\tau \sim \pi_t} \left[ D_{\text{KL}}(\pi(\cdot|s) \| \pi(\cdot|s)) \right] \leq \epsilon, \end{aligned} \tag{2} πt+1=πargmaxEτ∼πt[πt(a∣s)π(a∣s)Aπt(s,a)]s.t. Eτ∼πt[DKL(π(⋅∣s)∥π(⋅∣s))]≤ϵ,(2)
π ( a ∣ s ) π t ( a ∣ s ) \frac{\pi(a|s)}{\pi_t(a|s)} πt(a∣s)π(a∣s):新 / 旧策略在状态s下选择动作a的概率比值(衡量策略的变化幅度);
A π t ( s , a ) A^{\pi_t}(s,a) Aπt(s,a):优势函数(表示 "在状态s选动作a,比选旧策略的平均动作更好多少");
D KL ( ⋅ ∥ ⋅ ) D_{\text{KL}}(\cdot\|\cdot) DKL(⋅∥⋅):KL 散度(衡量新 / 旧策略的差异,避免策略更新幅度过大导致训练不稳定);
ϵ \epsilon ϵ:置信域大小(限制 KL 散度的上限,控制策略更新的 "安全幅度")。
其中 A π t ( s , a ) : = ∑ i ν i A R i π t ( s , a ) − ∑ j λ t j A C j π t ( s , a ) A^{\pi_t}(s,a) := \sum_i \nu_i A_{R_i}^{\pi_t}(s,a) - \sum_j \lambda_t j A_{C_j}^{\pi_t}(s,a) Aπt(s,a):=∑iνiARiπt(s,a)−∑jλtjACjπt(s,a), ϵ \epsilon ϵ是置信域大小, D KL D_{\text{KL}} DKL是 KL 散度。关于权重 ν \nu ν与 λ \lambda λ的条件,可参考 [14] 中的定理 4.2。
A R i π t ( s , a ) A_{R_i}^{\pi_t}(s,a) ARiπt(s,a):第i个奖励目标对应的优势函数(衡量动作a对 "提升目标i" 的贡献);
A C j π t ( s , a ) A_{C_j}^{\pi_t}(s,a) ACjπt(s,a):第j个约束成本对应的优势函数(衡量动作a对 "违反约束j" 的风险);
为合理确定权重 ν \nu ν与 λ \lambda λ,我们采用了两种方法:1. 奖励归一化;2. 优势函数的标准差归一化。
首先,在 CMORL 设定中,每个奖励函数的量级不同,因此必须将其调整到一致水平。为此,我们对每个奖励与阶段应用奖励归一化,并使用归一化后的奖励训练价值函数 ------ 这种方法可自动将每个目标的比例调整到一致水平。
同奖励 / 约束的优势函数 "量级不同 "(比如 "跳跃高度" 的优势是 "几十","关节限制" 的优势是 "几"),导致权重 ν / λ \nu/\lambda ν/λ难以合理设置,甚至让策略 "只关注量级大的项,忽略量级小的项"。
其次,保持奖励与成本在 "量级" 与 "目标 - 约束比例" 上的一致性至关重要。若比例不一致,策略可能会过度最大化目标而忽略约束,进而破坏训练过程的稳定性。为解决这一问题,我们通过各自的标准差对奖励与成本优势函数进行归一化,确保策略以一致的目标 - 约束比例更新。
最终,所提优势函数聚合规则如下: A π = A R π Std [ A R π ] − η ∑ j A C j π Std [ A C j π ] 1 ( J C j ( π ) > d j ) , (3) A^\pi = \frac{A_R^\pi}{\text{Std}[A_R^\pi]} - \eta \sum_j \frac{A_{C_j}^\pi}{\text{Std}[A_{C_j}^\pi]} \boldsymbol{1}(J_{C_j}(\pi) > d_j), \tag{3} Aπ=Std[ARπ]ARπ−ηj∑Std[ACjπ]ACjπ1(JCj(π)>dj),(3)
其中 Std \text{Std} Std表示标准差, A R π : = ∑ i ω i A ^ R i π A_R^\pi := \sum_i \omega_i \hat{A}{R_i}^\pi ARπ:=∑iωiA^Riπ ( ω (\omega (ω是给定偏好, A ^ R i π \hat{A}{R_i}^\pi A^Riπ是由归一化奖励计算得到的优势函数),超参数 η \eta η用作约束的比例系数(与 [16] 中的设置一致)。
让 "奖励优势" 和 "约束优势" 的量级一致,保证策略在 "提升目标" 和 "满足约束" 之间的平衡,避免训练不稳定。
结合聚合后的优势函数,可通过式 (2) 更新策略。但为简化实现,我们采用 PPO 更新,其形式如下 [15]: π t + 1 = arg max π E τ ∼ π t [ min ( r t A π t , clip ( r t , 1 − ϵ , 1 + ϵ ) A π t ) ] , \pi_{t+1} = \argmax_{\pi} \mathbb{E}_{\tau \sim \pi_t} \left[ \min(r_t A^{\pi_t}, \text{clip}(r_t, 1-\epsilon, 1+\epsilon) A^{\pi_t}) \right], πt+1=πargmaxEτ∼πt[min(rtAπt,clip(rt,1−ϵ,1+ϵ)Aπt)],其中 r t : = π ( a ∣ s ) / π t ( a ∣ s ) r_t := \pi(a|s)/\pi_t(a|s) rt:=π(a∣s)/πt(a∣s), ϵ \epsilon ϵ超参数。
TRPO(Trust Region Policy Optimization,置信域策略优化)是强化学习中经典的 "稳定策略更新" 算法,它通过KL 散度约束保证 "新策略与旧策略的差异不超过安全范围",从而避免策略更新幅度过大导致训练崩溃。
但是需要计算 "自然梯度""共轭梯度" 等复杂的优化步骤,工程落地成本高;每次更新都要额外计算 KL 散度的约束,训练效率较低。
因此,文中选择用 PPO(Proximal Policy Optimization,近端策略优化) 替代 TRPO------PPO 是 TRPO 的 "简化版",用更简单的 "裁剪机制" 实现了近似的 "置信域约束",同时保留了 TRPO 的稳定性优势。
仿真到真实技术
为将仿真训练的策略部署到真实环境,我们采用了两种广泛使用的 "仿真到真实" 技术:1. 域随机化;2. 师生学习[1,30,34]。
对于域随机化,我们遵循 [2] 中提出的 RL 方法:随机化电机强度与偏移、重力、摩擦力、恢复系数,以及关节位置、速度与基础姿态的噪声。随机化范围的细节见 [2] 的附录。
其次,师生学习 [1] 用于将使用特权信息(包含额外状态)的教师策略,提炼为仅依赖传感器数据(如关节位置、基础姿态)的学生策略。该过程与 [1] 中提出的方法类似,但动作执行方式略有不同:在我们的方法中,教师与学生策略的动作会交替提供给环境(固定间隔),这有助于收集与学生策略高度对齐的师生学习数据集。

实验部分
本节介绍了仿真与真实环境下的任务及其对应结果。关于训练后策略生成的动作细节,以及每个任务对应的奖励与成本函数。
环境设置
我们使用 Isaac Gym 仿真器 [28],因为它在 "仿真到真实" 迁移中的高效性,以及在各类机器人平台上创建丰富任务的灵活性。
在仿真实验中,我们采用了宇树机器人的两款机型:四足机器人 Go1 和人形机器人 H1 [35]。四足机器人包含 23 个身体连杆与 12 个电机,人形机器人则有 20 个身体连杆与 19 个电机。在真实环境实验中,通过 "仿真到真实" 技术,部署了四足机器人 Go1。
状态表示包含身体姿态、关节位置与速度、指令,以及上一步动作。对于教师策略,我们额外使用了 "特权信息"------ 例如线速度、角速度、高度、足部接触状态等,这些信息在真实环境中难以获取,但在仿真中是可用的。
任务细节
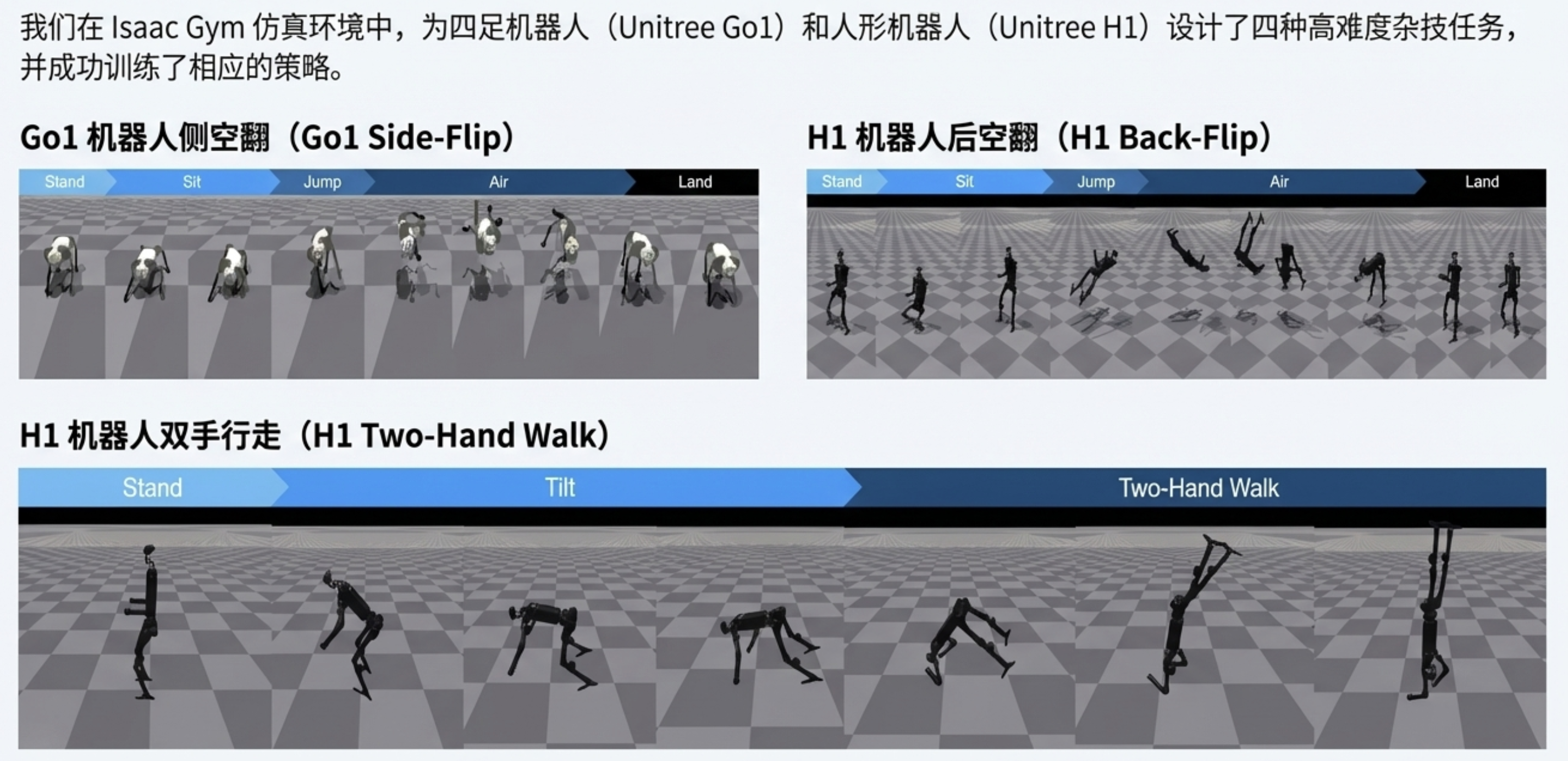
我们设计了四项杂技任务:后空翻、侧空翻、侧滚翻、双手行走。其中后空翻与双手行走任务在两种机器人上均有实现,侧滚翻与侧空翻则专为四足机器人设计。以下是每个任务的描述:
- 后空翻:机器人向后跳跃至空中,完成 360 度旋转且不触地,最终以初始姿态落地。任务的阶段转换及奖励、成本函数的设计,详见第四节 A 部分。
- 侧空翻:该任务与后空翻类似,但机器人是向右侧跳跃而非向后。其阶段转换与后空翻完全一致。
- 侧滚翻:机器人沿右侧完成完整翻滚,结束后回到初始姿态。该任务被划分为五个阶段:待机(Stand,机器人保持直立)、准备(Sit,机器人俯下身体准备翻滚)、半翻滚(Half-roll,机器人侧躺)、全翻滚(Full-roll,机器人完成翻滚)、恢复(Recover,机器人回到默认姿态与朝向)。
- 双手行走:机器人仅用双手(或前腿)行走并保持平衡。该任务被划分为三个阶段:待机(Stand,机器人保持默认姿态)、倾斜(Tilt,机器人放下前腿 / 手至地面,为行走做准备)、行走(Walk,机器人仅用双手完成行走)。
结果
机器人在仿真与真实环境中均成功完成了任务。在仿真中,机器人精准执行了所需动作,在侧滚翻与空翻任务中始终保持稳定,最终回到初始姿态。
在 Go1 的侧空翻任务中,机器人先降低高度,再向右侧旋转(翻滚角的变化可体现这一点);在 H1 的后空翻任务中,俯仰角与高度的变化表明机器人完成了向后翻转;在 H1 的双手行走任务中,智能体保持了稳定的平衡,持续交替双手支撑。
在 "仿真到真实" 实验中,机器人能够高精度复现所学行为。为了更详细地对比仿真与真实环境的性能,我们分析了任务全程中左前腿的关节位置与身体姿态的变化。机器人在仿真与真实环境中均成功完成了向后跳跃;在侧滚翻任务中,姿态变化与侧空翻任务呈现相似的规律;在双手行走任务中,俯仰角显示机器人向前倾斜,关节位置的波动则表明机器人通过反复抬放足部来维持平衡。
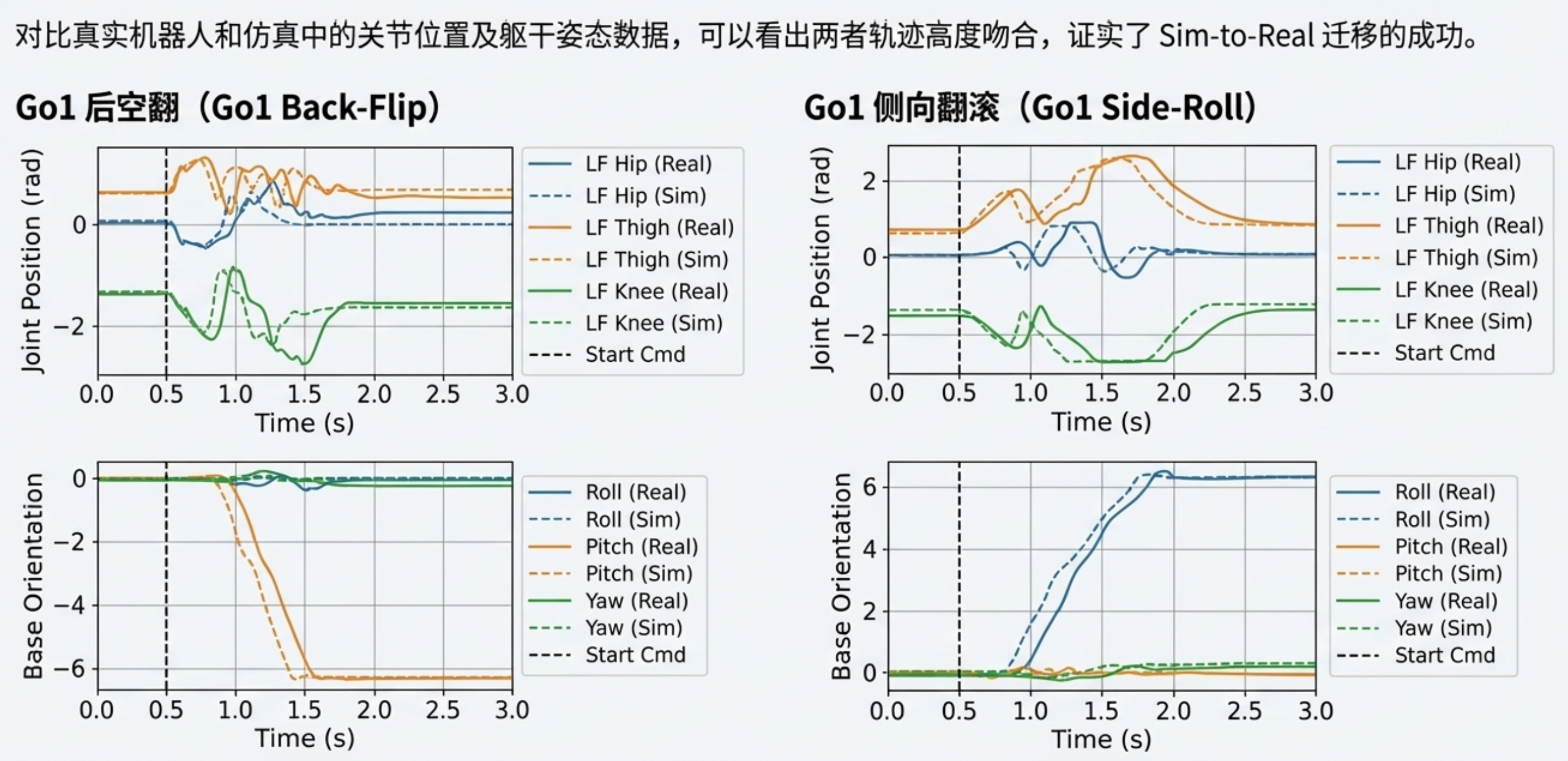
机器人的真实环境行为与仿真中的表现高度匹配,关节位置与姿态变化呈现相似的规律。这种高度相似性证实了 "仿真到真实" 过程的成功,说明训练后的策略被有效从仿真迁移到了真实环境。机器人在这些任务中的实际动作可参考附带视频。
消融实验
为验证 CMORL 的有效性,我们将所提方法与现有 RL 及约束 RL 算法在 Go1 的后空翻任务中进行了对比:
对于 RL 方法,我们采用了 PPO [15]:将多个奖励与成本函数加权求和,得到单一奖励函数;权重取自 CoMOPPO 训练过程中计算的目标与约束的平均比例。
对于约束 RL 方法,我们采用了惩罚 PPO(P3O)[16]:用与 PPO 相同的权重对多个奖励求和,得到单一奖励函数;约束则与 CoMOPPO 中的设置一致。
如图所示,CoMOPPO 是唯一成功完成任务的算法。与 CoMOPPO(在短暂的 "坐下""跳跃" 阶段后快速进入 "空中" 阶段)不同,另外两种算法主要停留在 "坐下" 阶段,说明它们无法正确执行跳跃动作。

结论

总结
- 该研究提出的"分阶段奖励"方法是如何运作的?
将一个复杂的序列任务分割成若干个不同的阶段,并为每个阶段单独定义奖励和成本函数。这种方式使得奖励函数的设计更加直观和简单。
- 阶段调度器的作用是什么?
根据用户定义的转换规则动态更新当前的执行阶段。根据逻辑判断将任务推向下一阶段,从而切换对应的奖励架构。
- 成本函数具体负责约束哪些方面?
保障机器人的物理安全和运动规范。放置身体碰撞,限制关节位置、速度和转矩在安全范围内。