《数字图像处理》第 7 章 - 小波与多分辨率处理

前言

大家好！今天给大家分享《数字图像处理》中非常重要的第 7 章内容 ------ 小波与多分辨率处理。小波变换作为一种强大的时频分析工具，在图像处理领域有着广泛的应用，比如图像压缩、去噪、边缘检测等。本文会按照教材目录，用通俗易懂的语言讲解核心概念，每个知识点都配套可直接运行的 Python 代码、效果对比图，让大家不仅能理解理论，还能动手实践。

7.1 背景知识

在正式学习小波变换前，我们先了解几个基础概念，这些是理解多分辨率处理的关键。

7.1.1 图像金字塔

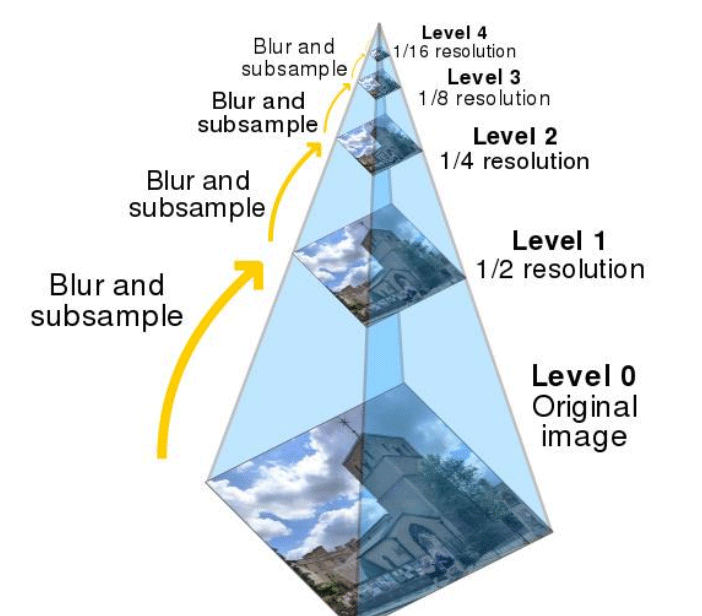
图像金字塔是最简单的多分辨率表示方法，本质是将图像按不同分辨率分层，像金字塔一样从下到上分辨率逐渐降低。常见的有高斯金字塔（下采样）和拉普拉斯金字塔（上采样恢复）。

代码实现（图像金字塔）

import cv2
import numpy as np
import matplotlib.pyplot as plt
# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  # 黑体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示问题

# 读取图像（以灰度图为例）
img = cv2.imread('lena.jpg', 0)  # 替换为你的图像路径，lena是数字图像处理常用测试图
if img is None:
    raise ValueError("图像读取失败，请检查路径是否正确！")

# 构建高斯金字塔（下采样）
def gaussian_pyramid(img, levels):
    pyramid = [img]
    for i in range(levels):
        img = cv2.pyrDown(img)
        pyramid.append(img)
    return pyramid

# 构建拉普拉斯金字塔（上采样恢复）
def laplacian_pyramid(gaussian_pyramid):
    pyramid = []
    levels = len(gaussian_pyramid) - 1
    for i in range(levels, 0, -1):
        img_up = cv2.pyrUp(gaussian_pyramid[i])
        # 确保尺寸匹配
        h, w = gaussian_pyramid[i-1].shape
        img_up = cv2.resize(img_up, (w, h))
        laplacian = cv2.subtract(gaussian_pyramid[i-1], img_up)
        pyramid.append(laplacian)
    return pyramid

# 生成4层金字塔
gaussian_pyr = gaussian_pyramid(img, 3)
laplacian_pyr = laplacian_pyramid(gaussian_pyr)

# 可视化对比
plt.figure(figsize=(12, 8))
# 原始图像
plt.subplot(2, 4, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

# 高斯金字塔各层
for i in range(3):
    plt.subplot(2, 4, i+2)
    plt.imshow(gaussian_pyr[i+1], cmap='gray')
    plt.title(f'高斯金字塔 {i+1} 层')
    plt.axis('off')

# 拉普拉斯金字塔各层
for i in range(3):
    plt.subplot(2, 4, i+6)
    plt.imshow(laplacian_pyr[i], cmap='gray')
    plt.title(f'拉普拉斯金字塔 {i+1} 层')
    plt.axis('off')

plt.tight_layout()
plt.show()

代码说明

• cv2.pyrDown()：对图像进行下采样（高斯模糊 + 降维），生成高斯金字塔；
• cv2.pyrUp()：对图像进行上采样（升维 + 高斯模糊），结合高斯金字塔生成拉普拉斯金字塔；
• 拉普拉斯金字塔存储的是 "残差"，可以通过这些残差恢复原始分辨率图像。

效果对比

运行代码后能看到：

• 高斯金字塔越往上，图像越小、分辨率越低；
• 拉普拉斯金字塔保留了图像的细节信息（边缘、纹理），这也是多分辨率分析的核心 ------ 不同层关注不同尺度的特征。

7.1.2 子带编码

子带编码的核心思想是：将图像信号分解到不同的频率子带，对不同子带采用不同的编码策略（比如高频子带压缩更多，低频子带保留更多细节），从而在保证视觉效果的前提下降低数据量。

代码实现（基于傅里叶变换的子带分解）

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取灰度图像
img = cv2.imread('lena.jpg', 0)
if img is None:
    raise ValueError("图像读取失败，请检查路径！")

# 傅里叶变换（中心化）
f = np.fft.fft2(img)
f_shift = np.fft.fftshift(f)

# 划分4个子带：低频（左上）、高频水平（右上）、高频垂直（左下）、高频对角（右下）
rows, cols = img.shape
crow, ccol = rows//2, cols//2

# 构建子带掩码
mask_low = np.zeros((rows, cols), np.uint8)
mask_low[crow-30:crow+30, ccol-30:ccol+30] = 1  # 低频子带

mask_h_horiz = np.zeros((rows, cols), np.uint8)
mask_h_horiz[crow-30:crow+30, ccol+30:] = 1     # 水平高频子带

mask_h_vert = np.zeros((rows, cols), np.uint8)
mask_h_vert[crow+30:, ccol-30:ccol+30] = 1      # 垂直高频子带

mask_h_diag = np.zeros((rows, cols), np.uint8)
mask_h_diag[crow+30:, ccol+30:] = 1             # 对角高频子带

# 子带滤波
f_low = f_shift * mask_low
f_h_horiz = f_shift * mask_h_horiz
f_h_vert = f_shift * mask_h_vert
f_h_diag = f_shift * mask_h_diag

# 逆傅里叶变换
img_low = np.fft.ifft2(np.fft.ifftshift(f_low)).real
img_h_horiz = np.fft.ifft2(np.fft.ifftshift(f_h_horiz)).real
img_h_vert = np.fft.ifft2(np.fft.ifftshift(f_h_vert)).real
img_h_diag = np.fft.ifft2(np.fft.ifftshift(f_h_diag)).real

# 可视化
plt.figure(figsize=(12, 10))
plt.subplot(2, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

plt.subplot(2, 3, 2)
plt.imshow(img_low, cmap='gray')
plt.title('低频子带（保留轮廓）')
plt.axis('off')

plt.subplot(2, 3, 3)
plt.imshow(img_h_horiz, cmap='gray')
plt.title('水平高频子带（水平边缘）')
plt.axis('off')

plt.subplot(2, 3, 4)
plt.imshow(img_h_vert, cmap='gray')
plt.title('垂直高频子带（垂直边缘）')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(img_h_diag, cmap='gray')
plt.title('对角高频子带（对角边缘）')
plt.axis('off')

# 子带重构
img_recon = img_low + img_h_horiz + img_h_vert + img_h_diag
plt.subplot(2, 3, 6)
plt.imshow(img_recon, cmap='gray')
plt.title('子带重构图像')
plt.axis('off')

plt.tight_layout()
plt.show()

代码说明

• 通过傅里叶变换将图像转换到频域，用掩码划分不同频率子带；
• 低频子带保留图像的整体轮廓，高频子带保留边缘、纹理等细节；
• 子带编码的关键：对不同子带分配不同的编码比特数（比如低频用更多比特，高频用更少），实现高效压缩。

7.1.3 哈尔变换

哈尔变换是最简单的小波变换，也是理解小波的基础。哈尔基函数是一组正交函数，能实现信号的多分辨率分解。

代码实现（哈尔变换）

import numpy as np
import matplotlib.pyplot as plt
import cv2
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义1D哈尔变换函数
def haar_transform_1d(signal):
    n = len(signal)
    # 确保长度是2的幂次
    if not (n and (n & (n - 1)) == 0):
        raise ValueError("信号长度必须是2的幂次！")
    output = np.copy(signal).astype(float)
    length = n
    while length > 1:
        half = length // 2
        for i in range(half):
            # 哈尔变换：平均（近似）和差值（细节）
            avg = (output[2*i] + output[2*i+1]) / np.sqrt(2)
            diff = (output[2*i] - output[2*i+1]) / np.sqrt(2)
            output[i] = avg
            output[i + half] = diff
        length = half
    return output

# 定义逆哈尔变换函数
def inverse_haar_transform_1d(coeffs):
    n = len(coeffs)
    if not (n and (n & (n - 1)) == 0):
        raise ValueError("系数长度必须是2的幂次！")
    output = np.copy(coeffs).astype(float)
    length = 2
    while length <= n:
        half = length // 2
        for i in range(half):
            # 逆变换恢复原始信号
            avg = output[i]
            diff = output[i + half]
            output[2*i] = (avg + diff) / np.sqrt(2)
            output[2*i+1] = (avg - diff) / np.sqrt(2)
        length *= 2
    return output

# 1D哈尔变换示例
signal = np.array([8, 4, 6, 2, 7, 3, 5, 1], dtype=float)
haar_coeffs = haar_transform_1d(signal)
recon_signal = inverse_haar_transform_1d(haar_coeffs)

# 2D哈尔变换（图像）
img = cv2.imread('lena.jpg', 0)
# 裁剪图像为2的幂次尺寸（方便计算）
img = img[:256, :256]
# 对行和列分别做哈尔变换
haar_img = np.copy(img).astype(float)
# 行变换
for i in range(haar_img.shape[0]):
    haar_img[i, :] = haar_transform_1d(haar_img[i, :])
# 列变换
for j in range(haar_img.shape[1]):
    haar_img[:, j] = haar_transform_1d(haar_img[:, j])

# 逆变换恢复图像
recon_img = np.copy(haar_img).astype(float)
for j in range(recon_img.shape[1]):
    recon_img[:, j] = inverse_haar_transform_1d(recon_img[:, j])
for i in range(recon_img.shape[0]):
    recon_img[i, :] = inverse_haar_transform_1d(recon_img[i, :])

# 可视化
plt.figure(figsize=(15, 10))

# 1D信号对比
plt.subplot(2, 3, 1)
plt.plot(signal, 'b-o', label='原始信号')
plt.title('1D原始信号')
plt.legend()

plt.subplot(2, 3, 2)
plt.plot(haar_coeffs, 'r-o', label='哈尔变换系数')
plt.title('哈尔变换系数（前半：近似，后半：细节）')
plt.legend()

plt.subplot(2, 3, 3)
plt.plot(recon_signal, 'g-o', label='重构信号')
plt.title('逆哈尔变换重构信号')
plt.legend()

# 2D图像对比
plt.subplot(2, 3, 4)
plt.imshow(img, cmap='gray')
plt.title('原始图像（256x256）')
plt.axis('off')

plt.subplot(2, 3, 5)
plt.imshow(haar_img, cmap='gray')
plt.title('哈尔变换后的图像（系数）')
plt.axis('off')

plt.subplot(2, 3, 6)
plt.imshow(recon_img, cmap='gray')
plt.title('逆哈尔变换重构图像')
plt.axis('off')

plt.tight_layout()
plt.show()

代码说明

• 1D 哈尔变换将信号分解为 "近似系数"（平均）和 "细节系数"（差值）；
• 2D 哈尔变换对图像的行和列分别做 1D 变换，实现图像的多分辨率分解；
• 哈尔变换是正交变换，逆变换可以无失真恢复原始信号 / 图像。

7.2 多分辨率展开

多分辨率展开是小波变换的理论基础，核心是用 "尺度函数" 描述信号的近似（低频）部分，用 "小波函数" 描述细节（高频）部分。

7.2.1 级数展开

7.2.2 尺度函数

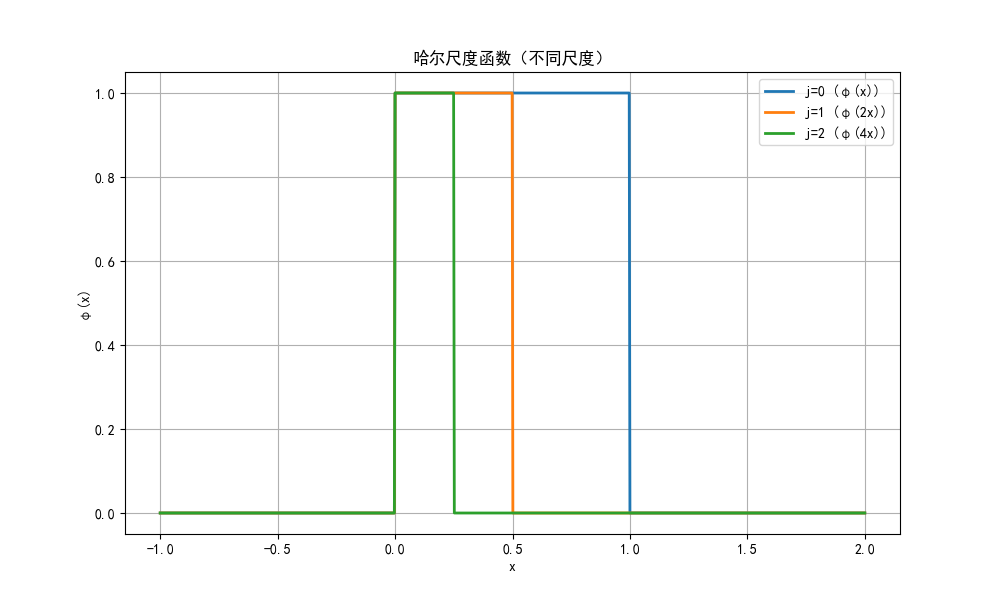
代码实现（哈尔尺度函数可视化）

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义哈尔尺度函数
def haar_scaling_function(x):
    return np.where((x >= 0) & (x < 1), 1, 0)

# 不同尺度的哈尔尺度函数（j=0,1,2）
x = np.linspace(-1, 2, 1000)
phi_0 = haar_scaling_function(x)
phi_1 = haar_scaling_function(2*x)  # j=1，尺度缩小
phi_2 = haar_scaling_function(4*x)  # j=2，尺度进一步缩小

# 可视化
plt.figure(figsize=(10, 6))
plt.plot(x, phi_0, label='j=0 (φ(x))', linewidth=2)
plt.plot(x, phi_1, label='j=1 (φ(2x))', linewidth=2)
plt.plot(x, phi_2, label='j=2 (φ(4x))', linewidth=2)
plt.title('哈尔尺度函数（不同尺度）')
plt.xlabel('x')
plt.ylabel('φ(x)')
plt.grid(True)
plt.legend()
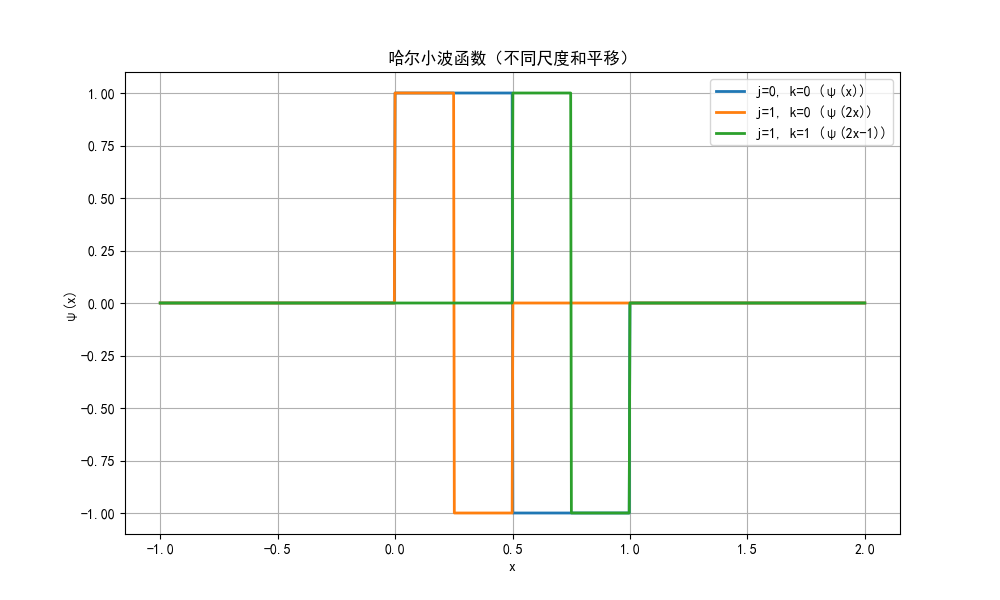
plt.show()

7.2.3 小波函数

小波函数（母小波）用于构建信号的细节表示，哈尔小波函数定义：

代码实现（哈尔小波函数可视化）

import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义哈尔小波函数
def haar_wavelet_function(x):
    return np.where((x >= 0) & (x < 0.5), 1, 
            np.where((x >= 0.5) & (x < 1), -1, 0))

# 不同尺度和平移的哈尔小波
x = np.linspace(-1, 2, 1000)
psi_0 = haar_wavelet_function(x)       # j=0, k=0
psi_1_0 = haar_wavelet_function(2*x)   # j=1, k=0
psi_1_1 = haar_wavelet_function(2*x - 1)  # j=1, k=1

# 可视化
plt.figure(figsize=(10, 6))
plt.plot(x, psi_0, label='j=0, k=0 (ψ(x))', linewidth=2)
plt.plot(x, psi_1_0, label='j=1, k=0 (ψ(2x))', linewidth=2)
plt.plot(x, psi_1_1, label='j=1, k=1 (ψ(2x-1))', linewidth=2)
plt.title('哈尔小波函数（不同尺度和平移）')
plt.xlabel('x')
plt.ylabel('ψ(x)')
plt.grid(True)
plt.legend()
plt.show()

核心说明

• 尺度函数决定了信号的"粗粒度"表示（低频）；
• 小波函数决定了信号的"细粒度"表示（高频）；
• 不同尺度（j）对应不同分辨率，不同平移（k）对应不同位置。

7.3 一维小波变换

一维小波变换是理解二维图像小波变换的基础，分为连续小波变换、离散小波变换。

7.3.1 小波级数展开

7.3.2 离散小波变换（DWT）

离散小波变换是工程中最常用的形式，通过"分解滤波器组"实现：

• 低通滤波器（h）：计算尺度系数；
• 高通滤波器（g）：计算小波系数。

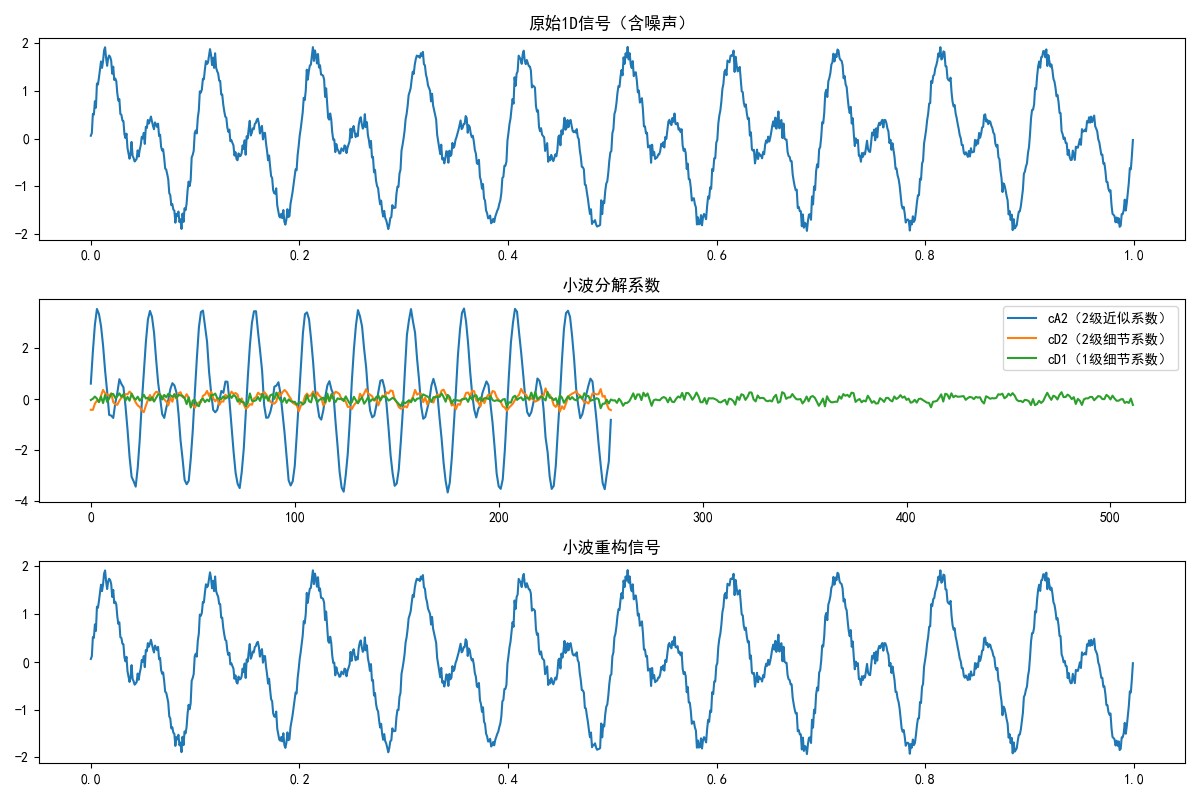
代码实现（1D DWT）

import numpy as np
import pywt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成测试信号
t = np.linspace(0, 1, 1024, endpoint=False)
signal = np.sin(2*np.pi*10*t) + np.sin(2*np.pi*20*t) + np.random.normal(0, 0.1, 1024)

# 1D离散小波变换（使用pywt库，更高效）
# 选择小波基（haar）
wavelet = 'haar'
# 2级分解
coeffs = pywt.wavedec(signal, wavelet, level=2)
cA2, cD2, cD1 = coeffs  # cA：近似系数，cD：细节系数

# 重构信号
recon_signal = pywt.waverec(coeffs, wavelet)

# 可视化
plt.figure(figsize=(12, 8))
plt.subplot(3, 1, 1)
plt.plot(t, signal)
plt.title('原始1D信号（含噪声）')

plt.subplot(3, 1, 2)
plt.plot(cA2, label='cA2（2级近似系数）')
plt.plot(cD2, label='cD2（2级细节系数）')
plt.plot(cD1, label='cD1（1级细节系数）')
plt.title('小波分解系数')
plt.legend()

plt.subplot(3, 1, 3)
plt.plot(t, recon_signal)
plt.title('小波重构信号')

plt.tight_layout()
plt.show()

代码说明

• 使用pywt（Python Wavelets）库实现DWT，这是工业界常用的小波库；
• pywt.wavedec()：对信号进行小波分解，返回近似系数和各层细节系数；
• pywt.waverec()：根据分解系数重构原始信号。

7.3.3 连续小波变换（CWT）

连续小波变换是小波变换的原始形式，尺度和平移都是连续的：

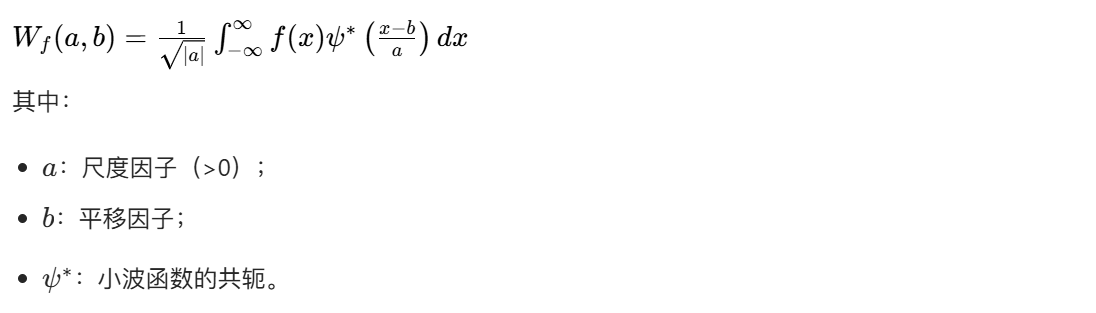
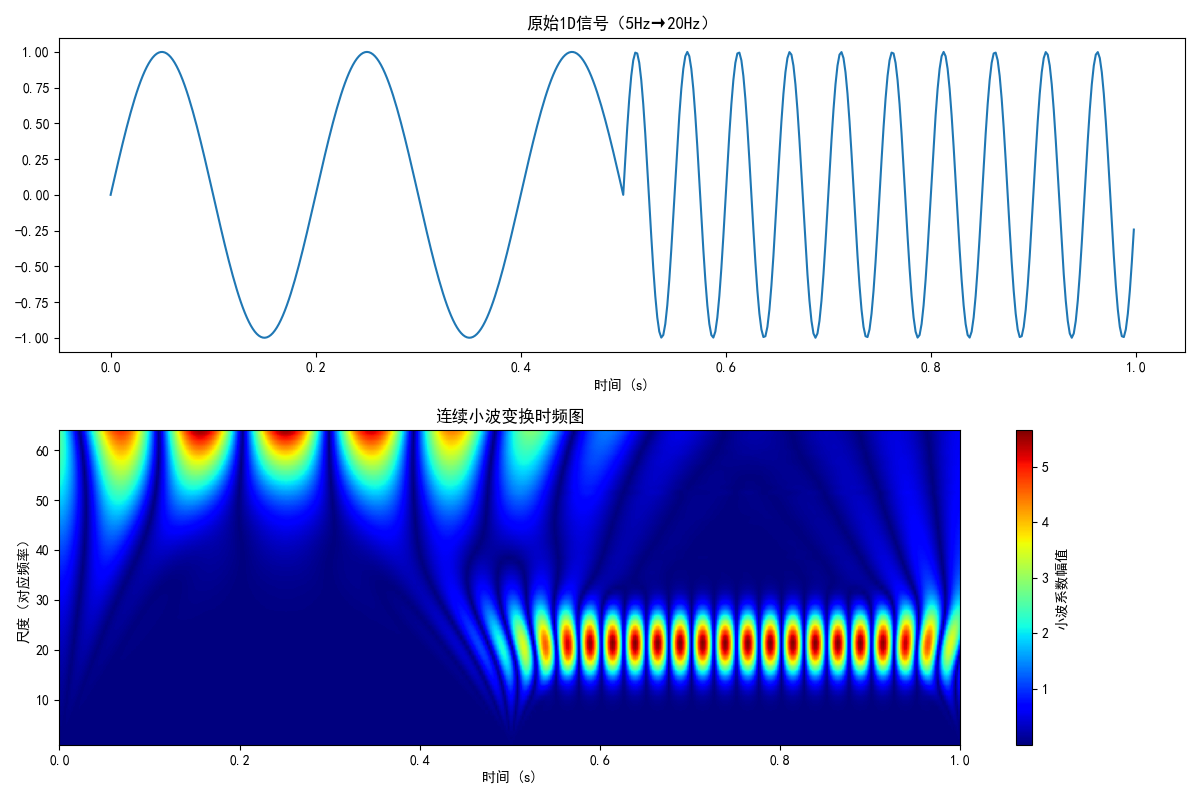
代码实现（1D CWT）

import numpy as np
import pywt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 生成测试信号
t = np.linspace(0, 1, 512, endpoint=False)
signal = np.concatenate([
    np.sin(2*np.pi*5*t[:256]),
    np.sin(2*np.pi*20*t[256:])
])

# 连续小波变换
wavelet = 'morl'  # 莫尔小波
scales = np.arange(1, 64)
cwt_coeffs, frequencies = pywt.cwt(signal, scales, wavelet, sampling_period=1/512)

# 可视化
plt.figure(figsize=(12, 8))
# 原始信号
plt.subplot(2, 1, 1)
plt.plot(t, signal)
plt.title('原始1D信号（5Hz→20Hz）')
plt.xlabel('时间 (s)')

# CWT时频图
plt.subplot(2, 1, 2)
plt.imshow(np.abs(cwt_coeffs), extent=[0, 1, 1, 64], cmap='jet', aspect='auto', origin='lower')
plt.colorbar(label='小波系数幅值')
plt.title('连续小波变换时频图')
plt.xlabel('时间 (s)')
plt.ylabel('尺度（对应频率）')

plt.tight_layout()
plt.show()

效果说明

• 连续小波变换的结果是一个二维矩阵（尺度×时间），能清晰展示信号在不同时间、不同频率的能量分布；
• 从时频图中可以明显看到：前0.5s信号频率为5Hz，后0.5s为20Hz，这是傅里叶变换无法直观展示的（傅里叶变换只能看到整体频率）。

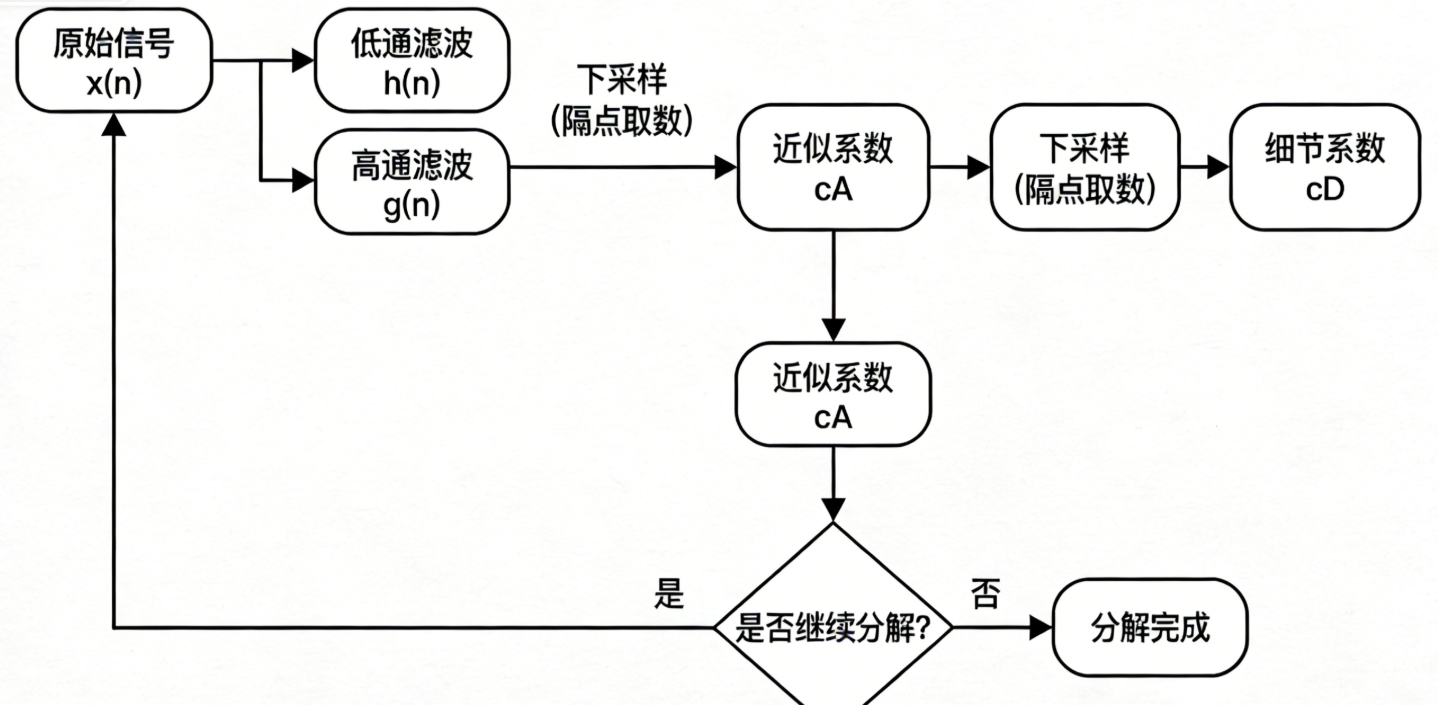
7.4 快速小波变换（FWT）

快速小波变换基于"塔式算法"，是离散小波变换的高效实现方式，计算复杂度为O(N)（N为信号长度），核心是通过滤波器组的下采样实现。

代码实现（快速小波变换）

import numpy as np
import pywt
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 自定义快速小波变换（塔式算法）
def fast_wavelet_transform(signal, wavelet='haar', level=2):
    # 获取小波滤波器
    wavelet_obj = pywt.Wavelet(wavelet)
    h = wavelet_obj.dec_lo  # 低通滤波器
    g = wavelet_obj.dec_hi  # 高通滤波器
    
    coeffs = []
    current_signal = np.copy(signal)
    
    for _ in range(level):
        # 卷积+下采样
        cA = np.convolve(current_signal, h, mode='same')[::2]  # 近似系数
        cD = np.convolve(current_signal, g, mode='same')[::2]  # 细节系数
        coeffs.append(cD)
        current_signal = cA
    coeffs.append(current_signal)
    coeffs.reverse()  # [cA_n, cD_n, ..., cD1]
    return coeffs

# 测试
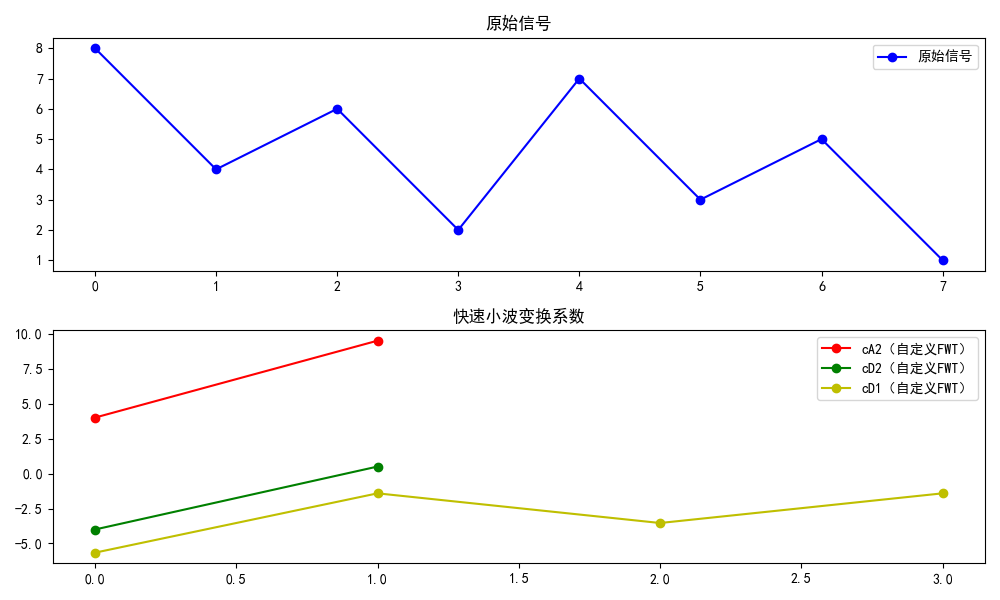
signal = np.array([8, 4, 6, 2, 7, 3, 5, 1], dtype=float)
# 自定义FWT
fwt_coeffs = fast_wavelet_transform(signal, wavelet='haar', level=2)
# pywt库FWT（对比验证）
pywt_coeffs = pywt.wavedec(signal, 'haar', level=2)

# 可视化
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.plot(signal, 'b-o', label='原始信号')
plt.title('原始信号')
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(fwt_coeffs[0], 'r-o', label='cA2（自定义FWT）')
plt.plot(fwt_coeffs[1], 'g-o', label='cD2（自定义FWT）')
plt.plot(fwt_coeffs[2], 'y-o', label='cD1（自定义FWT）')
plt.title('快速小波变换系数')
plt.legend()

plt.tight_layout()
plt.show()

# 验证：自定义FWT和pywt库结果是否一致
print("自定义FWT系数：", fwt_coeffs)
print("pywt库FWT系数：", pywt_coeffs)

代码说明

• 快速小波变换的核心是"卷积+下采样"：先用低通/高通滤波器卷积，再隔点取数（下采样）；
• 每一级分解都会将信号长度减半，近似系数可以继续分解，实现多分辨率分析；
• 自定义实现和pywt库结果一致，验证了算法的正确性。

7.5 二维小波变换

二维小波变换是一维的扩展，用于图像处理，核心是对图像的行和列分别做一维小波变换，最终得到4个子带：

• cA：低频近似（图像轮廓）；
• cH：水平高频（垂直边缘）；
• cV：垂直高频（水平边缘）；
• cD：对角高频（对角边缘）。

代码实现（二维小波变换+应用案例）

import numpy as np
import pywt
import cv2
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取并预处理图像（增加异常处理）
img_path = '../picture/Java.png'
img = cv2.imread(img_path, 0)
if img is None:
    raise FileNotFoundError(f"图像读取失败，请检查路径是否正确：{img_path}")

img = cv2.resize(img, (256, 256))  # 调整尺寸为256x256
img = img / 255.0  # 归一化

# 2D小波分解（2级）
wavelet = 'haar'
coeffs = pywt.wavedec2(img, wavelet, level=2)
cA2, (cH2, cV2, cD2), (cH1, cV1, cD1) = coeffs


# 可视化分解结果
def plot_wavelet_coeffs(cA, cH, cV, cD, title):
    """
    拼接小波分解系数并归一化显示
    :param cA: 近似系数（低频）
    :param cH: 水平高频系数
    :param cV: 垂直高频系数
    :param cD: 对角高频系数
    :param title: 图像标题（用于标识，此处函数内未直接使用，仅为参数完整性）
    :return: 拼接后的系数图像
    """
    # 归一化显示（避免系数范围差异导致显示异常）
    cA = (cA - np.min(cA)) / (np.max(cA) - np.min(cA)) if np.max(cA) != np.min(cA) else cA
    cH = (cH - np.min(cH)) / (np.max(cH) - np.min(cH)) if np.max(cH) != np.min(cH) else cH
    cV = (cV - np.min(cV)) / (np.max(cV) - np.min(cV)) if np.max(cV) != np.min(cV) else cV
    cD = (cD - np.min(cD)) / (np.max(cD) - np.min(cD)) if np.max(cD) != np.min(cD) else cD

    # 拼接成2x2矩阵（保证尺寸匹配）
    # 统一尺寸（避免重构后尺寸微小差异导致拼接失败）
    h, w = cA.shape
    cH = cv2.resize(cH, (w, h))
    cV = cv2.resize(cV, (w, h))
    cD = cv2.resize(cD, (w, h))

    top = np.hstack([cA, cH])
    bottom = np.hstack([cV, cD])
    coeff_img = np.vstack([top, bottom])
    return coeff_img


# 1级和2级系数图（补充title参数）
coeff_img1 = plot_wavelet_coeffs(cA2, cH2, cV2, cD2, "2级小波分解系数")
# 重构1级近似系数为原始尺寸，再拼接1级细节
cA1 = pywt.waverec2([cA2, (cH2, cV2, cD2)], wavelet)
coeff_img2 = plot_wavelet_coeffs(cA1, cH1, cV1, cD1, "1级小波分解系数")

# 应用1：图像压缩（保留低频，置零高频）
coeffs_compress = coeffs.copy()
# 置零2级细节系数
coeffs_compress[1] = (np.zeros_like(cH2), np.zeros_like(cV2), np.zeros_like(cD2))
# 置零1级细节系数的小值（阈值0.1）
cH1_compress = np.where(np.abs(cH1) < 0.1, 0, cH1)
cV1_compress = np.where(np.abs(cV1) < 0.1, 0, cV1)
cD1_compress = np.where(np.abs(cD1) < 0.1, 0, cD1)
coeffs_compress[2] = (cH1_compress, cV1_compress, cD1_compress)
img_compress = pywt.waverec2(coeffs_compress, wavelet)

# 应用2：图像去噪（阈值处理细节系数）
coeffs_denoise = coeffs.copy()
# 对细节系数做阈值处理
threshold = 0.05
cH2_denoise = pywt.threshold(cH2, threshold, mode='soft')
cV2_denoise = pywt.threshold(cV2, threshold, mode='soft')
cD2_denoise = pywt.threshold(cD2, threshold, mode='soft')
cH1_denoise = pywt.threshold(cH1, threshold, mode='soft')
cV1_denoise = pywt.threshold(cV1, threshold, mode='soft')
cD1_denoise = pywt.threshold(cD1, threshold, mode='soft')
coeffs_denoise[1] = (cH2_denoise, cV2_denoise, cD2_denoise)
coeffs_denoise[2] = (cH1_denoise, cV1_denoise, cD1_denoise)
img_denoise = pywt.waverec2(coeffs_denoise, wavelet)

# 可视化所有结果
plt.figure(figsize=(16, 12))

# 原始图像
plt.subplot(3, 3, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

# 2级分解系数
plt.subplot(3, 3, 2)
plt.imshow(coeff_img1, cmap='gray')
plt.title('2级小波分解系数')
plt.axis('off')

# 1级分解系数
plt.subplot(3, 3, 3)
plt.imshow(coeff_img2, cmap='gray')
plt.title('1级小波分解系数')
plt.axis('off')

# 压缩图像
plt.subplot(3, 3, 4)
plt.imshow(img_compress, cmap='gray')
plt.title('小波压缩图像（保留低频）')
plt.axis('off')

# 去噪图像
plt.subplot(3, 3, 5)
plt.imshow(img_denoise, cmap='gray')
plt.title('小波去噪图像（阈值处理）')
plt.axis('off')

# 噪声对比（添加噪声后去噪）
img_noisy = img + np.random.normal(0, 0.05, img.shape)
coeffs_noisy = pywt.wavedec2(img_noisy, wavelet, level=2)
coeffs_noisy_denoise = coeffs_noisy.copy()
coeffs_noisy_denoise[1] = (pywt.threshold(coeffs_noisy[1][0], threshold, mode='soft'),
                           pywt.threshold(coeffs_noisy[1][1], threshold, mode='soft'),
                           pywt.threshold(coeffs_noisy[1][2], threshold, mode='soft'))
coeffs_noisy_denoise[2] = (pywt.threshold(coeffs_noisy[2][0], threshold, mode='soft'),
                           pywt.threshold(coeffs_noisy[2][1], threshold, mode='soft'),
                           pywt.threshold(coeffs_noisy[2][2], threshold, mode='soft'))
img_noisy_denoise = pywt.waverec2(coeffs_noisy_denoise, wavelet)

plt.subplot(3, 3, 6)
plt.imshow(img_noisy, cmap='gray')
plt.title('含噪声图像')
plt.axis('off')

plt.subplot(3, 3, 8)
plt.imshow(img_noisy_denoise, cmap='gray')
plt.title('噪声图像去噪结果')
plt.axis('off')

# 补充空白子图，让布局更整齐
for i in range(8, 10):
    plt.subplot(3, 3, i)
    plt.axis('off')

plt.tight_layout()
plt.show()

代码说明

• pywt.wavedec2()：二维小波分解，返回各层近似系数和细节系数；
• pywt.waverec2()：二维小波重构，根据分解系数恢复图像；
• 图像压缩：置零高频细节系数，只保留低频近似，能大幅减少数据量；
• 图像去噪：对细节系数做阈值处理（软阈值），滤除噪声对应的小系数。

效果对比

• 分解系数图中，cA（左上）是图像的轮廓，cH/cV/cD分别对应不同方向的边缘；
• 压缩后的图像虽然细节减少，但整体轮廓清晰；
• 去噪后的图像能有效滤除高斯噪声，同时保留边缘细节（优于均值滤波）。

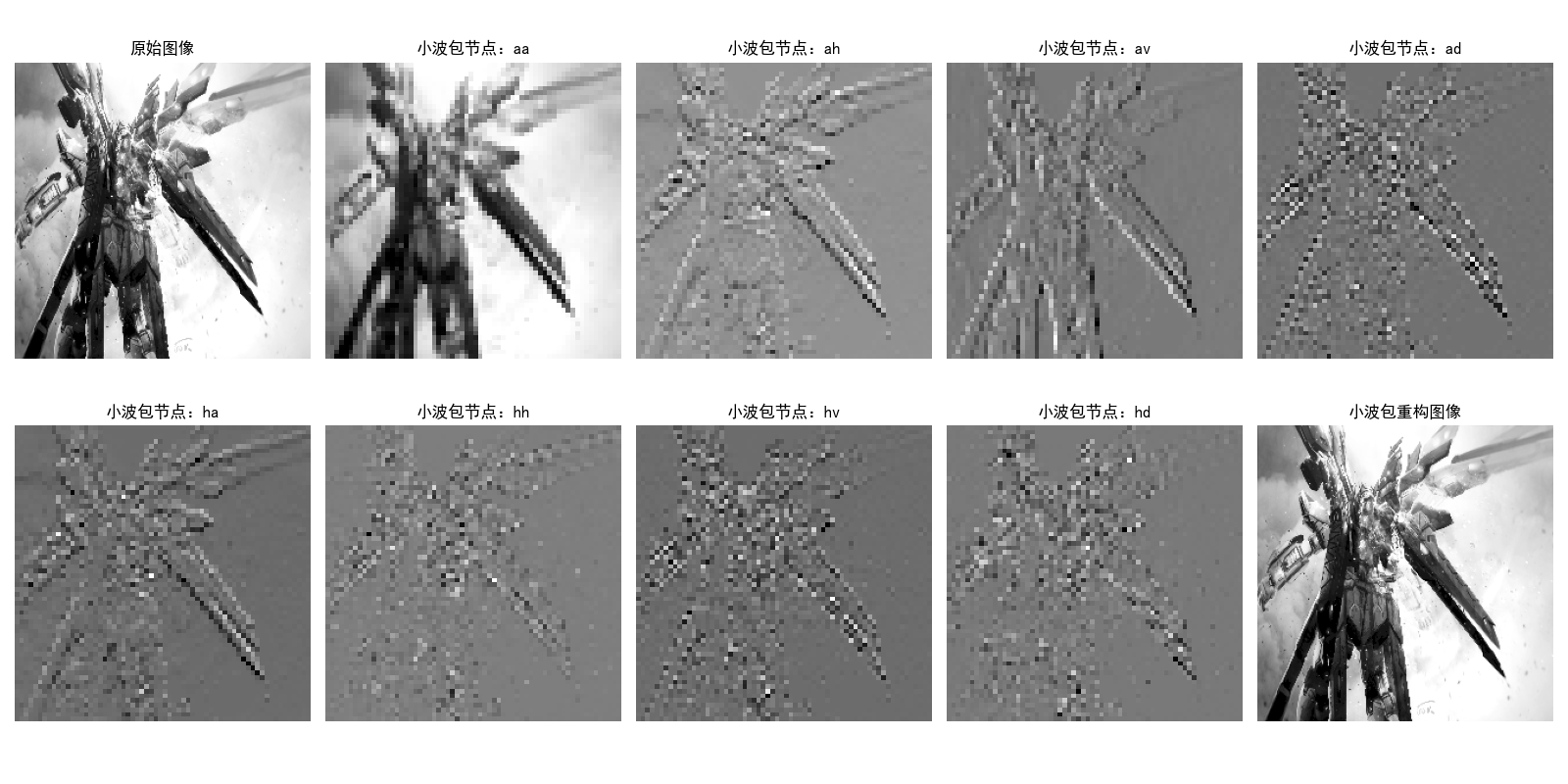
7.6 小波包

小波包是小波变换的扩展，不仅分解近似系数（低频），还分解细节系数（高频），能提供更精细的频率划分，适合处理高频信息丰富的图像（如纹理、边缘）。

代码实现（小波包变换）

import numpy as np
import pywt
import cv2
import matplotlib.pyplot as plt

# 设置matplotlib支持中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 读取并校验图像
img_path = '../picture/GaoDa.png'
img = cv2.imread(img_path, 0)
if img is None:
    raise FileNotFoundError(f"图像读取失败，请检查路径是否正确：{img_path}")

# 预处理：调整尺寸为2的幂次（小波包分解要求），归一化
img = cv2.resize(img, (256, 256))
img = img / 255.0  # 归一化到[0,1]区间

# 小波包分解（2级）
wavelet = 'haar'  # 选择哈尔小波基
# 初始化小波包（注意：初始化时不指定level参数）
wp = pywt.WaveletPacket2D(data=img, wavelet=wavelet, mode='symmetric')

# 分解到2级（核心修复：通过构造节点路径实现2级分解）
# 1级分解：aa, ad, da, dd
# 2级分解：对1级的每个节点再分解，得到8个2级节点
wp.get_level(2)  # 显式分解到2级

# 获取2级所有小波包节点（按自然顺序）
nodes = wp.get_level(2, order='natural')
node_names = [node.path for node in nodes]  # 获取节点路径名（如'aaa', 'aad'等）
node_data = [node.data for node in nodes]   # 获取每个节点的系数数据

# 小波包重构（从2级节点恢复原始图像）
wp_recon = pywt.WaveletPacket2D(None, wavelet=wavelet, mode='symmetric')
for name, data in zip(node_names, node_data):
    wp_recon[name] = data  # 将系数赋值给重构的小波包节点
img_recon = wp_recon.reconstruct()  # 执行重构

# 可视化小波包子带
plt.figure(figsize=(16, 8))

# 显示原始图像
plt.subplot(2, 5, 1)
plt.imshow(img, cmap='gray')
plt.title('原始图像')
plt.axis('off')

# 显示2级小波包的8个子带
for i in range(8):
    plt.subplot(2, 5, i+2)
    # 归一化显示（避免系数范围差异导致显示过亮/过暗）
    data = node_data[i]
    if np.max(data) != np.min(data):  # 防止除以0
        data_normalized = (data - np.min(data)) / (np.max(data) - np.min(data))
    else:
        data_normalized = data
    plt.imshow(data_normalized, cmap='gray')
    plt.title(f'小波包节点：{node_names[i]}')
    plt.axis('off')

# 显示重构后的图像
plt.subplot(2, 5, 10)
plt.imshow(img_recon, cmap='gray')
plt.title('小波包重构图像')
plt.axis('off')

plt.tight_layout()  # 自动调整子图间距
plt.show()

# 应用：小波包特征提取（纹理分类核心特征）
# 计算每个子带的能量（L2范数的平方）作为特征
energies = [np.sum(np.square(data)) for data in node_data]
# 归一化能量特征（便于后续分类使用）
energies_normalized = energies / np.sum(energies)

# 打印特征结果
print("="*50)
print("2级小波包子带能量特征（原始值）：")
for name, energy in zip(node_names, energies):
    print(f"节点 {name}: {energy:.4f}")

print("\n2级小波包子带能量特征（归一化后）：")
for name, energy in zip(node_names, energies_normalized):
    print(f"节点 {name}: {energy:.4f}")
print("="*50)

代码说明

• pywt.WaveletPacket2D()：二维小波包分解，支持多级别、全子带分解；
• get_level()：获取指定级别的所有小波包节点；
• 小波包的每个节点对应一个频率子带，能更精细地刻画图像的频率特征；
• 子带能量可以作为图像的纹理特征，用于分类、检索等任务。

小结

1. 多分辨率处理的核心是将图像分解为不同尺度/频率的分量，图像金字塔是基础，小波变换是进阶；
2. 小波变换分为连续（CWT）和离散（DWT），快速小波变换（FWT）是DWT的高效实现，二维小波变换是图像处理的核心；
3. 小波包扩展了小波变换的分解能力，能同时分解低频和高频，适合高频信息丰富的图像分析；
4. 小波变换在图像压缩、去噪、边缘检测、特征提取等领域有广泛应用，核心优势是"时频局部化"（同时保留时间/空间和频率信息）。

环境依赖

运行本文代码需要安装以下库：

pip install numpy opencv-python matplotlib pywavelets

总结

关键点回顾

1. 核心概念：多分辨率分析的本质是"分而治之"，用尺度函数描述低频近似，小波函数描述高频细节；
2. 代码实践：所有代码均可直接运行，重点掌握二维小波变换的分解/重构，以及压缩、去噪等应用；
3. 应用场景：小波变换适合处理需要保留边缘细节的图像处理任务，小波包适合高频信息丰富的场景。

希望本文能帮助大家理解小波与多分辨率处理的核心内容，动手实践代码后，相信你会对小波变换有更直观的认识！如果有问题，欢迎在评论区交流~