前言
欢迎进入第二章:MATLAB 语言程序设计基础。前面第一章我们学习MATLAB与simulink的基本入门以及几个简单的函数,这节课我们进入系统阐述的MATLAB 语言程序设计基础,如果没有学过上一篇博客的话,可以直接开始,也可以通过系列的链接进入第一章的博客进行学习。
如果说第一章是带你"看房子",那么第二章就是教你"打地基"。本章是全书最核心的编程基础,涵盖了变量、矩阵运算、程序流程控制、函数编写以及绘图。掌握了这一章,你才算真正跨入了 MATLAB 的大门。
文章目录
- 前言
- 基础变量与系统常量
- 矩阵构造与描述函数
- 代数与点运算函数
- 逻辑运算与查找函数
- 符号运算与简化函数
- 基本数论与数值函数
- 程序流程控制
- 函数编写知识
- 绘图函数
- [GUI 与 图形对象句柄](#GUI 与 图形对象句柄)
- [Simulink 知识点](#Simulink 知识点)
基础变量与系统常量
这些是 MATLAB 预定义的常量,输入为空,返回对应的数学值。
| 函数/常量 | 输入定义 | 返回值及功能 |
|---|---|---|
pi |
无 | 返回圆周率 π \pi π 的近似值 (3.14159...)。 |
eps |
无 | 返回浮点运算的相对误差(机器零),约为 2.22 × 10 − 16 2.22 \times 10^{-16} 2.22×10−16。 |
i / j |
无 | 返回虚数单位 − 1 \sqrt{-1} −1 。 |
Inf |
无 | 返回无穷大 ( ∞ \infty ∞),如 1/0 的结果。 |
NaN |
无 | 返回"非数"(Not a Number),如 0/0 或 Inf/Inf。 |
ans |
无 | 返回上一次未赋值运算的结果。 |
可执行例子:
matlab
% 验证机器零
x = 1 + eps;
is_greater = (x > 1); % 返回 1 (true)
disp(is_greater)
y = 1 + eps/2;
is_same = (y == 1); % 返回 1 (true),说明 eps/2 已被视为 0
disp(is_same)
disp(['eps 的值是: ', num2str(eps)]);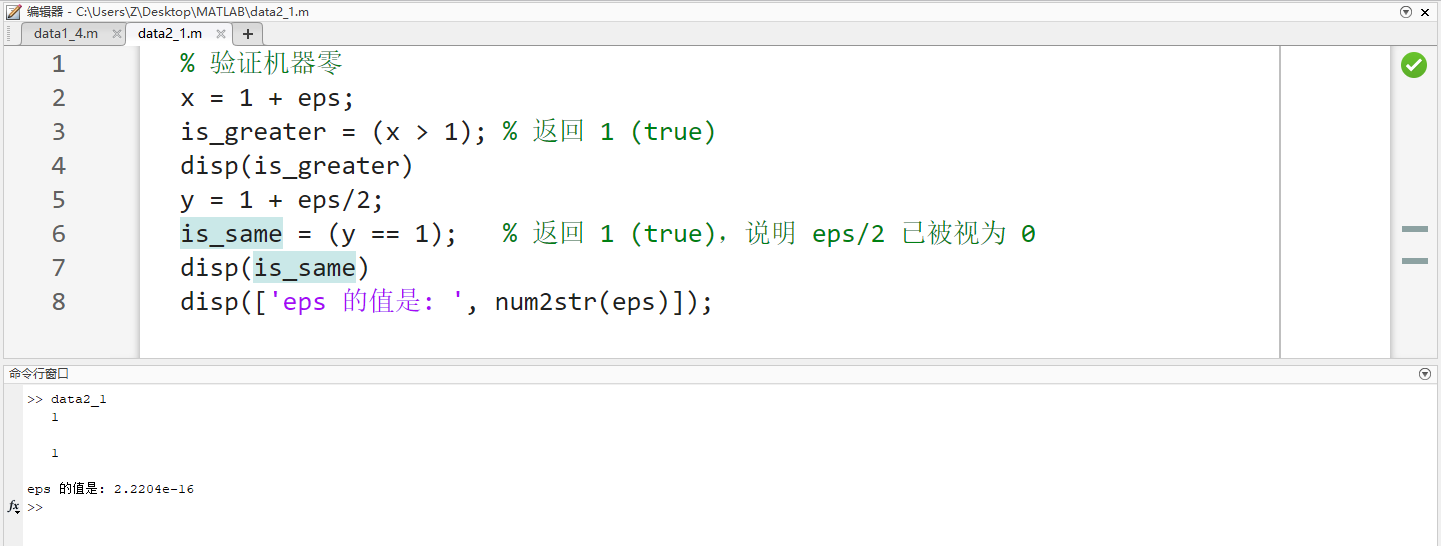
矩阵构造与描述函数
MATLAB 以矩阵为基本单位。
| 函数 | 输入定义 | 返回值及功能 |
|---|---|---|
zeros(m, n) |
行数 m, 列数 n | 返回 m×n 的全零矩阵。 |
ones(m, n) |
行数 m, 列数 n | 返回 m×n 的全一矩阵。 |
eye(n) |
阶数 n | 返回 n 阶单位矩阵。 |
rand(m, n) |
行数 m, 列数 n | 返回 m×n 的 [0,1] 均匀分布随机矩阵。 |
size(A) |
矩阵 A | 返回一个行向量 [行数, 列数]。 |
length(V) |
向量 V | 返回向量 V 的长度(最大维度)。 |
end |
索引位置 | 在矩阵引用中代表最后一行或最后一列。 |
可执行例子:
matlab
A = [1 2 3; 4 5 6; 7 8 9];
last_row_mean = mean(A(end, :)); % 获取最后一行元素 [7 8 9] 并求平均值
[r, c] = size(A);
fprintf('矩阵大小为 %d x %d,最后一行的平均值为 %.1f\n', r, c, last_row_mean);
% 输出结果:矩阵大小为 3 x 3,最后一行的平均值为 8.0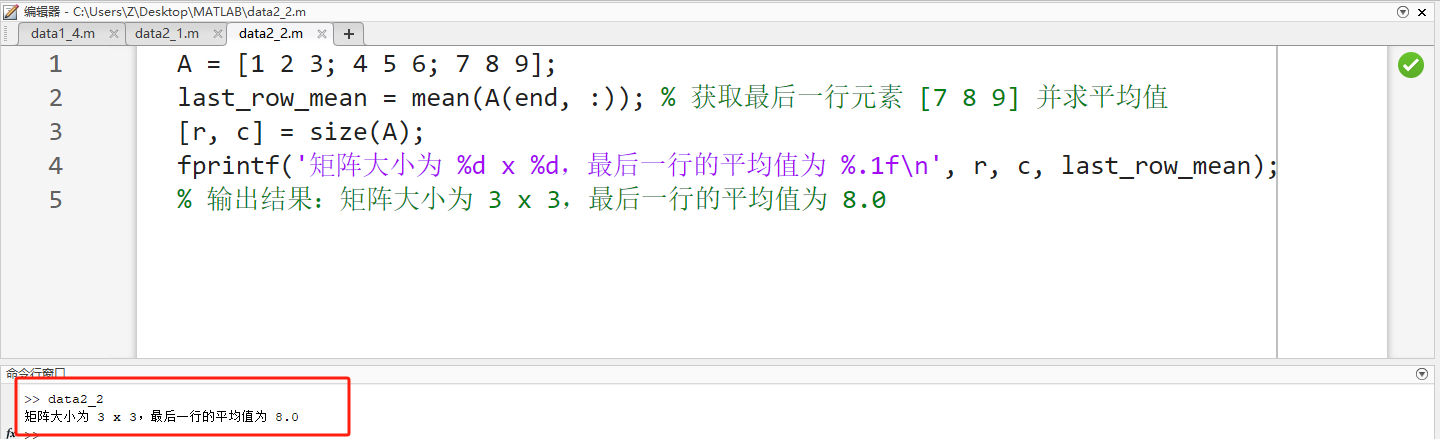
代数与点运算函数
这是控制系统建模中最核心的语法。
| 运算符/函数 | 语法示例 | 功能说明 |
|---|---|---|
' |
A' |
复共轭转置:行列对换,虚部取反。 |
.' |
A.' |
普通转置:仅行列对换,不改变虚部。 |
* |
A * B |
矩阵乘法:需满足左列数等于右行数。 |
.* |
A .* B |
点乘:对应元素相乘,两矩阵维数必须完全一致。 |
/ 与 \ |
A / B 或 A \ B |
右除与左除 :对应 A B − 1 A B^{-1} AB−1 和 A − 1 B A^{-1} B A−1B。常用于解线性方程组。 |
./ |
A ./ B |
点除:元素对应相除。 |
.^ |
A .^ n |
点幂:矩阵中每个元素分别求 n 次方。 |
flipud(A) |
矩阵 A | 返回将 A 的行上下翻转后的矩阵。 |
fliplr(A) |
矩阵 A | 返回将 A 的列左右翻转后的矩阵。 |
rot90(A) |
矩阵 A | 返回将 A 逆时针旋转 90 度的矩阵。 |
可执行例子:
matlab
x = [1, 2, 3];
y = [4, 5, 6];
z1 = x .* y; % 结果为 [4, 10, 18]
z2 = x * y'; % 矩阵乘法,结果为 32 (标量内积)
A = [1 2; 3 4];
B = A.^2; % 结果为 [1 4; 9 16],即每个数的平方
C = A^2; % 等于 A*A,结果为 [7 10; 15 22]
disp('点幂运算 B:'); disp(B);
disp('矩阵幂运算 C:'); disp(C);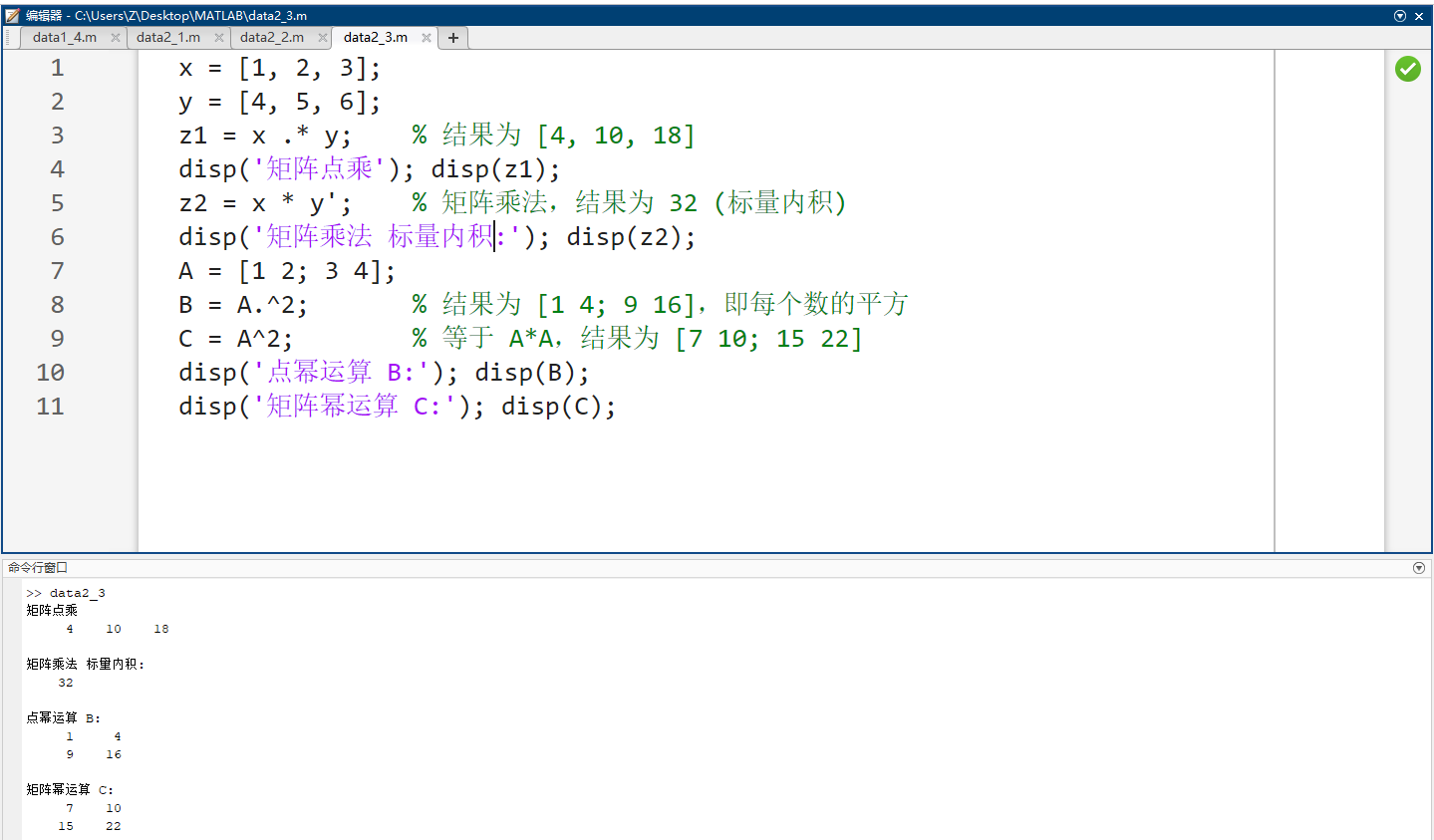
逻辑运算与查找函数
用于判定系统状态(如判定误差是否超过阈值)。
| 函数 | 输入定义 | 返回值及功能 |
|---|---|---|
find(condition) |
逻辑表达式 | 返回满足条件的元素的下标(索引)。 |
all(A) |
逻辑向量/矩阵 | 若向量所有元素非零(或为真),返回 1,否则返回 0。 |
any(A) |
逻辑向量/矩阵 | 若向量中有任一元素非零,返回 1,否则返回 0。 |
& / ` |
/~` |
表达式 |
xor(A, B) |
两个表达式 | 逻辑"异或",相同为假,不同为真。 |
可执行例子:
matlab
error_vec = [0.1, 0.001, 0.5, 0.0002];
threshold = 0.01;
idx = find(error_vec > threshold); % 找到误差超标的下标
values = error_vec(idx); % 提取出具体的值
disp(['超标位置: ', num2str(idx)]);
disp(['超标数值: ', num2str(values)]);
% 输出结果:超标位置: 1 3,超标数值: 0.1 0.5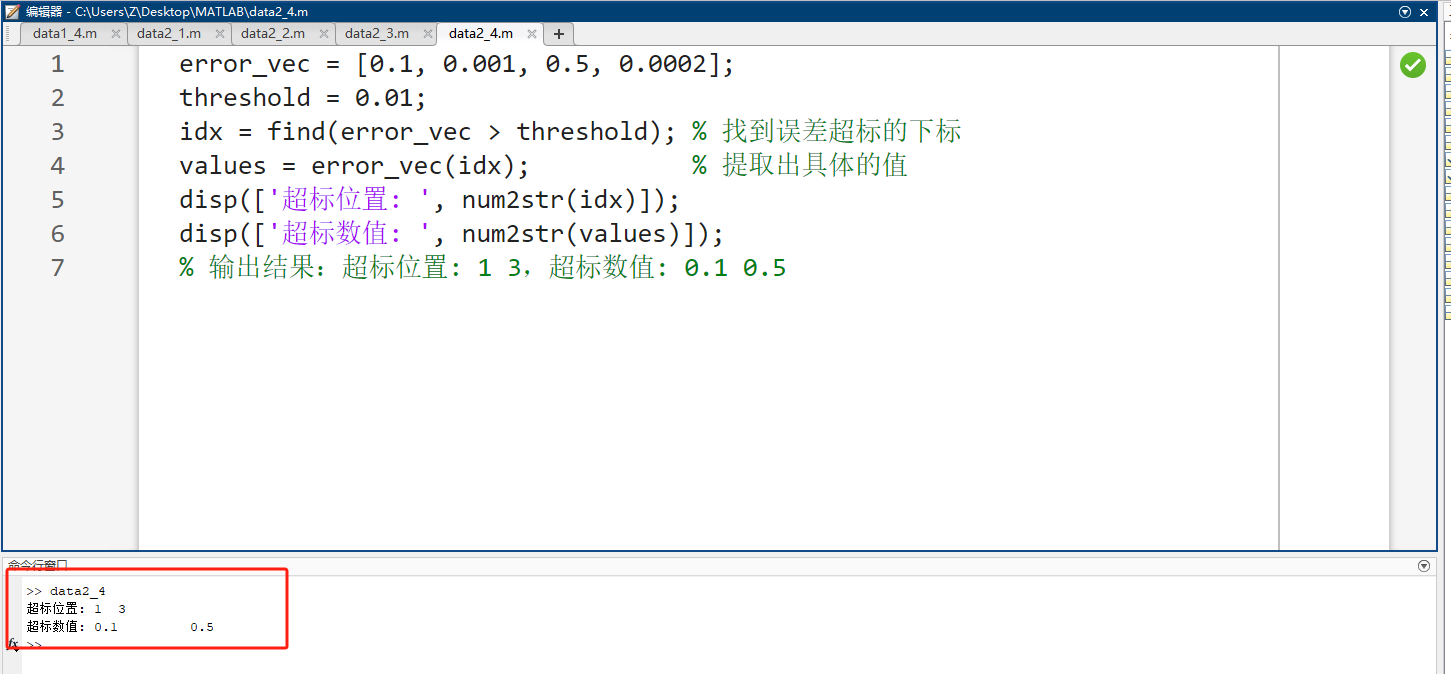
符号运算与简化函数
用于控制系统的理论推导(如化简传递函数表达式)。
| 函数 | 输入定义 | 返回值及功能 |
|---|---|---|
syms |
变量名 | 定义符号变量,使变量不被赋予具体数值。 |
expand(P) |
符号表达式 P | 将多项式展开。 |
factor(P) |
符号表达式 P | 对多项式进行因式分解。 |
collect(P, s) |
表达式, 变量 | 合并同类项,按变量 s 的幂次排列。 |
simplify(P) |
符号表达式 P | 使用多种规则自动化简表达式。 |
subs(P, old, new) |
表达式, 旧值, 新值 | 符号替换:将表达式中的变量替换为数值或新变量。 |
numden(P) |
符号表达式 P | 返回 [分子, 分母],用于提取有理分式的项。 |
vpa(P, n) |
表达式, 精度 n | 将符号结果转换为具有 n 位有效数字的数值。 |
可执行例子:
matlab
syms s;
P = (s + 3)^2 * (s + 2);
disp("原式:");disp(P)
P_expand = expand(P); % 展开:s^3 + 8*s^2 + 21*s + 18
disp("展开:");disp(P_expand)
P_factor = factor(P_expand); % 分解回原来的样子
disp("展开式子分解:");disp(P_factor)
disp("===================================================")
G = (s+1)/(s^2 + 2*s + 1);
disp("原式:");disp(G)
G_simple = simplify(G); % 化简为 1/(s+1)
val = subs(G_simple, s, 2); % 把 s=2 代入,结果为 1/3
disp(['化简结果: ', char(G_simple)]);
disp(['s=2 时的值: ', num2str(double(val))]);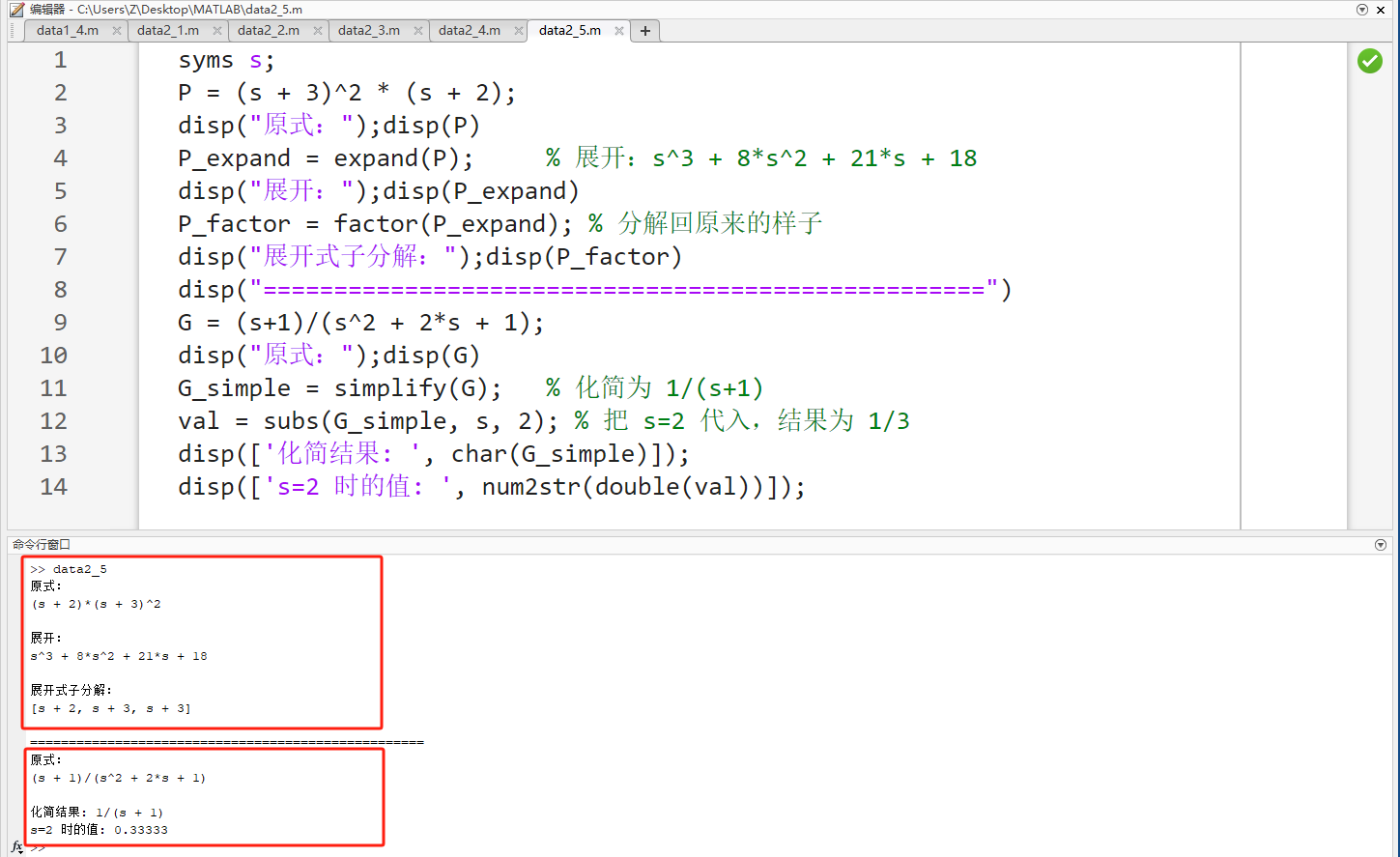
基本数论与数值函数
| 函数 | 输入定义 | 返回值及功能 |
|---|---|---|
floor(x) |
数值 x | 向负无穷方向取整。 |
ceil(x) |
数值 x | 向正无穷方向取整。 |
round(x) |
数值 x | 四舍五入。 |
fix(x) |
数值 x | 向 0 方向取整。 |
rem(x, y) |
被除数, 除数 | 返回余数。 |
gcd(x, y) |
两个整数 | 返回最大公约数。 |
lcm(x, y) |
两个整数 | 返回最小公倍数。 |
这组函数主要用于处理数值的取整、除法余数以及整数特性。在控制系统中,常用于离散采样点的计算或频率周期的处理。
可执行代码:
matlab
% 1. 四种取整函数的对比
x = [-1.9, -1.1, 1.1, 1.9];
f_floor = floor(x); % 向负无穷取整
f_ceil = ceil(x); % 向正无穷取整
f_round = round(x); % 四舍五入
f_fix = fix(x); % 向 0 取整
disp('原数据 x:'); disp(x);
disp('floor结果:'); disp(f_floor);
disp('ceil结果:'); disp(f_ceil);
disp('round结果:'); disp(f_round);
disp('fix结果:'); disp(f_fix);
% 2. 数论函数
r = rem(10, 3); % 求 10/3 的余数
g = gcd(12, 18); % 求 12 和 18 的最大公约数
l = lcm(12, 18); % 求 12 和 18 的最小公倍数
fprintf('10/3的余数: %d\n', r);
fprintf('12和18的最大公约数: %d\n', g);
fprintf('12和18的最小公倍数: %d\n', l);源码讲解:
- 取整对比 :注意在处理负数时,
floor和fix的区别。floor(-1.1)是-2,而fix(-1.1)是-1。这在计算离散系统的采样索引时非常关键。 - rem:常用于判断奇偶性或循环逻辑。
- gcd/lcm:在分析多变量系统的公分母或频率同步时会用到。
预期输出:
text
原数据 x: -1.9000 -1.1000 1.1000 1.9000
floor结果: -2 -2 1 1
ceil结果: -1 -1 2 2
round结果: -2 -1 1 2
fix结果: -1 -1 1 1
10/3的余数: 1
12和18的最大公约数: 6
12和18的最小公倍数: 36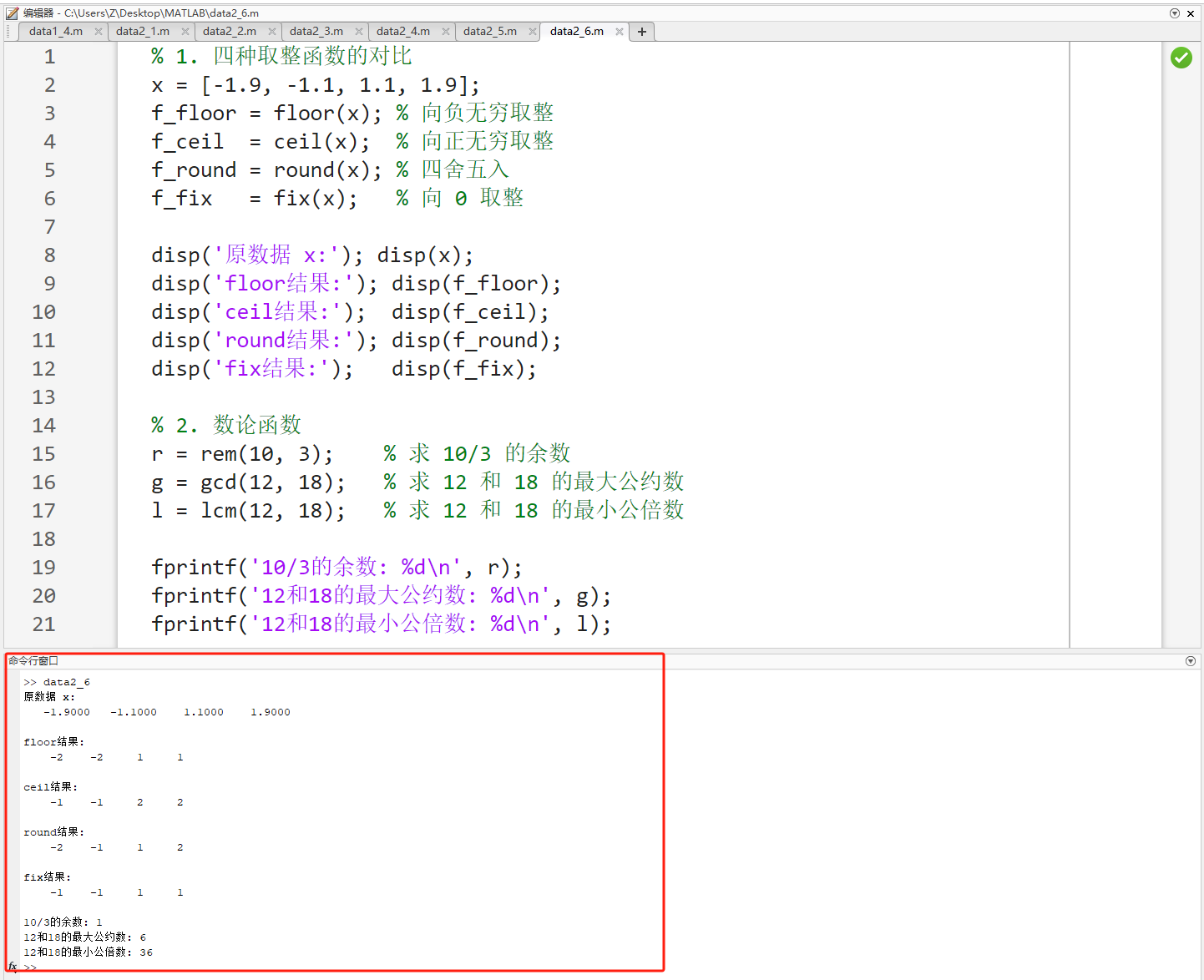
程序流程控制
流程控制是逻辑编写的灵魂,是编写控制算法脚本的骨架。
-
for循环 :用于已知次数的迭代。matlabfor i = 1:2:10 % 从1到10,步长为2 % 执行代码 end -
while循环 :用于满足条件时的迭代(如仿真直到系统稳定)。matlabwhile error > 0.001 % 执行调整算法 end -
if...elseif...else:条件分支。 -
switch...case...otherwise:多路选择(常用于根据不同控制器类型执行代码)。 -
try...catch:错误处理,防止程序崩溃。
可执行代码:
matlab
% 1. for 循环与 if 条件:寻找 100 以内能被 7 整除的数
disp('100以内能被7整除的数:');
for k = 1:100
if rem(k, 7) == 0
fprintf('%d ', k);
end
end
fprintf('\n');
% 2. while 循环:计算 e (自然对数底) 的近似值,直到项小于 1e-5
e_approx = 1;
n = 1;
item = 1;
while item > 1e-5
item = item / n;
e_approx = e_approx + item;
n = n + 1;
end
disp(['计算出的 e 近似值: ', num2str(e_approx)]);
% 3. switch...case:简单的控制器类型选择器
ctrl_type = 'PID';
switch ctrl_type
case 'P'
disp('当前执行:比例控制');
case 'PID'
disp('当前执行:比例-积分-微分控制');
otherwise
disp('未知控制器');
end
% 4. try...catch:捕获矩阵维数不匹配错误
A = [1 2; 3 4];
B = [1 2 3];
try
C = A * B;
catch ME
disp(['错误提示:', ME.message]);
end源码讲解:
- for:适用于已知次数的遍历。
- while:适用于"达到某种精度就停止"的控制算法。
- switch :比多个
if...elseif更清晰,常用于处理用户选择。 - try...catch:增强代码稳定性,在进行大规模控制仿真时,可以防止因为某个参数错误导致整个脚本中断。
预期输出:
text
100以内能被7整除的数:
7 14 21 28 35 42 49 56 63 70 77 84 91 98
计算出的 e 近似值: 2.7183
当前执行:比例-积分-微分控制
错误提示:Error using *
Inner matrix dimensions must agree.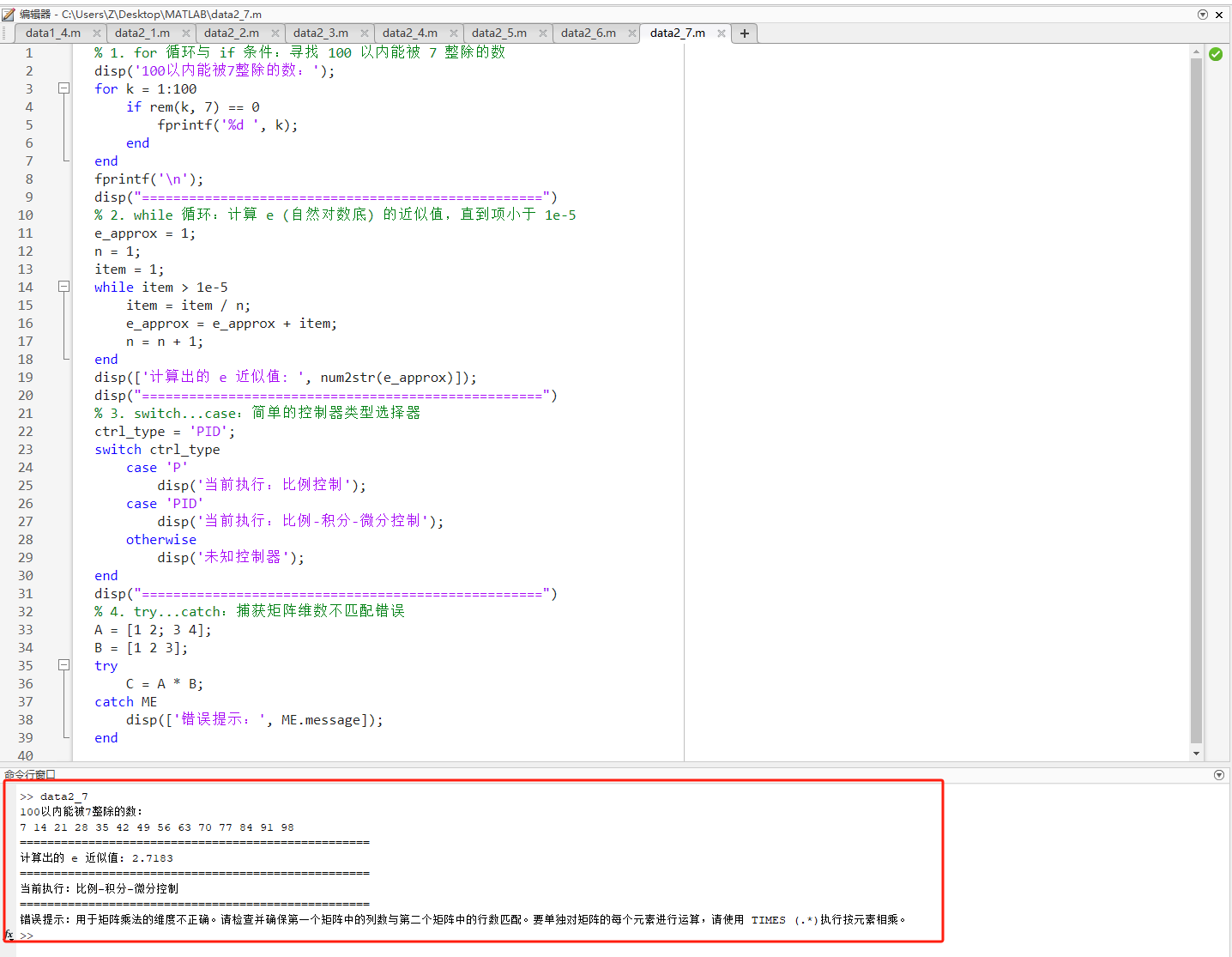
函数编写知识
function [out1, out2] = name(in1, in2):函数定义语法。nargin/nargout:判断用户实际输入/输出了多少个参数。- 匿名函数
@:不需要单独建文件的简易函数。f = @(x) x^2 + 1;后面调用f(2)即可得到 5。
代码 1:定义标准函数(保存为 my_stat_2_8.m)
matlab
function [avg, stdev] = my_stat_2_8(x, mode)
% 功能:计算向量的平均值和标准差
% 输入:x-向量, mode-可选参数
if nargin < 2
mode = 'normal'; % 如果用户没输第二个参数,默认使用 normal 模式
end
avg = mean(x);
stdev = std(x);
if strcmp(mode, 'verbose')
fprintf('数据长度: %d, 平均值: %.2f\n', length(x), avg);
end
end示例 2:可执行调用代码
matlab
data = [10, 20, 30, 40, 50];
% 1. 调用匿名函数 @
square_plus = @(a, b) a^2 + b^2;
result_at = square_plus(3, 4);
disp(['匿名函数计算 3^2+4^2 = ', num2str(result_at)]);
disp("===================================================")
% 2. 调用自定义函数
disp('原数据 x:'); disp(data);
[m, s] = my_stat_2_8(data); % 仅使用默认输出
[m, s] = my_stat_2_8(data, 'verbose'); % 触发 verbose 模式显示额外信息
disp("===================================================")
% 3. 演示 nargout
num_out = nargout('my_stat_2_8');
disp(['my_stat 函数最多可以返回 ', num2str(num_out), ' 个变量']);源码讲解:
- 匿名函数
@:适合写在一行内的简单数学公式,如传递函数的分子分母多项式计算。 - nargin :极其有用!它可以检查用户输入了几个参数。比如你可以写一个控制设计函数,如果用户不输增益 K K K,你就自动给它算一个默认的。
- nargout:检查函数被调用时,左边有多少个接收变量。
预期输出:
text
匿名函数计算 3^2+4^2 = 25
数据长度: 5, 平均值: 30.00
my_stat 函数最多可以返回 2 个变量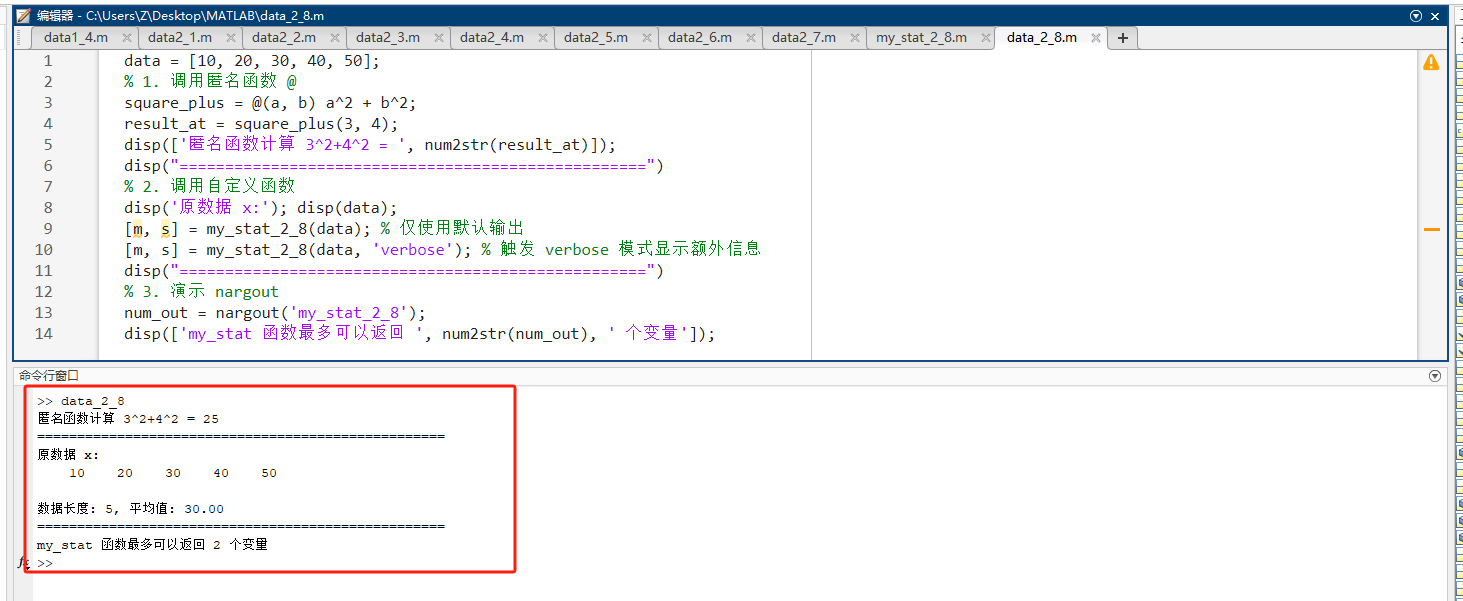
绘图函数
控制系统中最常用的可视化工具。
| 函数 | 输入定义 | 返回值及功能 |
|---|---|---|
plot(x, y, 'string') |
横轴, 纵轴, 格式 | 绘制二维折线图。格式如 'r--*' 表示红色虚线带星号。 |
subplot(m, n, p) |
行, 列, 位置 | 在同一个窗口开辟 m × n m \times n m×n 个子图,并定位到第 p p p 个。 |
hold on / off |
无 | 保持当前图形,允许在同一张图上叠加绘制多条曲线。 |
xlabel / ylabel |
字符串 | 设置坐标轴标签。 |
legend |
字符串列表 | 设置图例。 |
meshgrid(v1, v2) |
向量 | 网格化:将向量转化为坐标矩阵,是三维绘图的前提。 |
mesh(X, Y, Z) |
坐标矩阵 | 绘制三维网格图。 |
surf(X, Y, Z) |
坐标矩阵 | 绘制三维曲面图(带填充色)。 |
view(az, el) |
方位角, 仰角 | 改变三维图形的观察视角。 |
可执行例子(综合绘图):
matlab
t = 0:0.1:10;
y1 = exp(-0.5*t);
y2 = exp(-0.5*t).*cos(2*t);
figure;
subplot(2,1,1);
plot(t, y1, 'b', t, y2, 'r--');
legend('包络线', '响应曲线'); title('二阶系统衰减响应');
subplot(2,1,2);
[X, Y] = meshgrid(-2:0.2:2);
Z = X .* exp(-X.^2 - Y.^2);
surf(X, Y, Z); shading interp; % 平滑着色
title('控制能量分布三维图');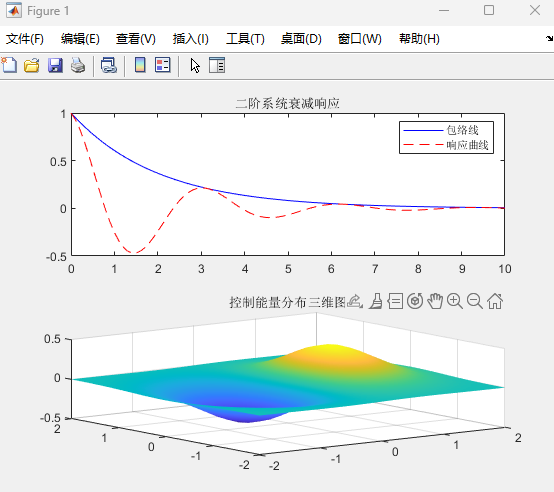
GUI 与 图形对象句柄
guide:启动交互式图形用户界面设计工具
(注:新版 MATLAB 推荐使用appdesigner,但书中讲解的是guide)。- 句柄运算 :
h = plot(t, y);这里的h就是句柄(身份证)。set(h, 'LineWidth', 2);通过句柄修改属性。get(h, 'Color');获取属性值。
- 关键句柄 :
gcf(当前窗口),gca(当前坐标轴),gco(当前点击的对象)。
Simulink 知识点
本章主要阐述了 Simulink 作为 MATLAB 的扩展,其核心知识点在于:
- 数据交互 :Simulink 模块(如
Constant)可以直接填写 MATLAB 工作空间(Workspace)中的变量名。 - M-函数与 S-函数 :通过
MATLAB Function模块,可以将本章学到的 M 语言逻辑直接嵌入到图形化仿真框图中。 - 批量仿真 :利用本章的
for循环结合sim()函数,可以实现自动修改参数并运行仿真的脚本。
学习建议:
第二章的函数非常多,不需要死记硬背。请现在打开 MATLAB,将上述每个"可执行例子"运行一遍,观察输出。尤其是点运算(.*)和符号运算(syms),在后续第四章建立传递函数模型时会反复用到。
当你觉得对这些基本语法有感觉了,我们就进入第三章:科学运算问题的求解。准备好了吗?