数据结构基础：从二叉树到多叉树数据结构进阶

引言：从二叉树到多叉树？

签名我们学习了二叉树，它的每个节点最多只有两个子节点。这是一种非常优美且高效的数据结构。但现实世界是复杂的，很多关系并不能简单地用"最多两个分支"来描述。

比如：

📁 一个文件系统的目录结构，一个文件夹下可以有任意多个文件或子文件夹。
🏢 一个公司的组织架构，一位经理可以管理多个下属。
🌐 一个HTML文档的DOM树，一个元素节点可以包含多个子元素节点。

这些场景用二叉树来直接表示会非常别扭。这时，多叉树，也叫"普通树"，就登场了。它允许每个节点拥有任意数量的子节点，完美契合这些复杂结构。

1、什么是多叉树

**定义：**多叉树是n（n≥0）个节点的有限集合。在任意一棵非空树中：

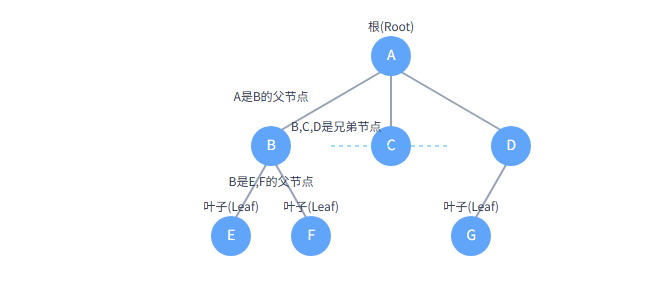
有且仅有一个特定的称为根的节点。
当n>1时，其余节点可分为m（m>0）个互不相交的有限集，其中每一个集合本身又是一棵树，并且称为根的子树

简单来说，就是不限制子节点数量的树形结构。

二叉树：每个节点最多有2个孩子（左孩子、右孩子）
多叉树：每个节点可以有0个、1个、2个或更多孩子

2、多叉树的性质

除了直观的定义，树结构还有一些非常重要的数学性质。理解它们能帮助我们更深刻地认识树的效率和约束。我们设一棵树的节点总数为 n。

2.1、性质1：节点数与边数关系

树中的边数 = 节点数 - 1

对于任何一棵非空树，其边的数量 E 总是比节点数量 n 少 1，即 E = n - 1。

为什么是n-1条边？

因为除了根节点外，每个节点都有且仅有一个父节点，从父节点到该节点有一条边。n个节点中，除根节点外有n-1个节点，因此有n-1条边。

2.2、性质2：节点数与度的关系

节点总数 = 所有节点的度数之和 + 1

一个节点的度指的是它拥有的子树（或孩子节点）的数量。那么，节点总数 n 等于树中所有节点的度数总和再加上 1。

在树中，每一条边都唯一地连接一个父节点和一个子节点。
因此，树中边的总数 E 必然等于所有子节点的总数。
而一个节点的"度"，就是它拥有的子节点数量。所以，将树中所有节点的度数相加，得到的结果就是这棵树所有子节点的总数，这个总数也等于边的总数 E。
即：Σ(所有节点的度数) = E
根据性质1 ，我们已经知道 E = n - 1。
将两个等式联立，我们得到：Σ(所有节点的度数) = n - 1。
稍作变形，即可得到：n = Σ(所有节点的度数) + 1。

2.3、性质3：在度为 m 的树中，第 i 层的节点数最多为 m ^i-1(i≥1)

这里的"度为m的树"指的是树中所有节点的度数都不超过 m。我们规定根节点在第1层。

我们可以一层一层地看：

第1层： 只有根节点，数量是 1。公式 m(1−1)=m0=1m^{(1-1)}=m^0=1m(1−1)=m0=1 成立。
第2层： 要让第2层节点最多，根节点就必须"开足马力"，长出最多的孩子。因为树的度是 m，所以它最多有 m 个孩子。第2层最多有 m个节点。公式 m2−1=m1=mm^{2-1}=m^1=mm2−1=m1=m成立。
第3层： 要让第3层节点最多，第2层的每个节点（最多m个）也都要长出最多的孩子（每个m个）。于是第3层最多有 m∗m=m2m*m=m^2m∗m=m2个节点。公式 m3−1=m2m^{3-1}=m^2m3−1=m2 成立。
以此类推... 第 i 层的最大节点数，就是第 i-1层的最大节点数再乘以 m，所以是 mi−2∗m=mi−1m^{i-2}*m=m^{i-1}mi−2∗m=mi−1。

它定义了树在每一层的"最大宽度"。这是分析树的算法（如广度优先搜索）空间复杂度的基础，也为我们推导下一个关于树总容量的性质打下了基础。

2.4、性质4：高度为 h、度为 m 的树，最多有 (m ^h+1- 1) / (m - 1) 个节点

根据我们的定义，高度为 h 的树，一共有 h+1 层。要让节点总数最多，我们就必须让从第1层到第 h+1 层的每一层都"长满"节点。

第1层 (h=0)：m0=1m^0=1m0=1
第2层 (h=1)m1m^1m1
...
第h+1层 (h=h)：mhm^hmh

将它们全部相加，就得到了总节点数的最大值：1+m+m2+...+mh1+m+m^2+...+m^h1+m+m2+...+mh

这是一个典型的等比数列求和 。根据求和公式，我们有：(mh+1−1)/(m−1)(m^h+1 - 1) / (m - 1)(mh+1−1)/(m−1)

它建立了树的高度(h) 和**总容量(N)**之间的直接关系。这个公式的反推形式尤其重要，引出了下一个性质。

2.5、性质5：具有 n 个节点的 m 叉树，最小高度为 ⌈log _m(n(m-1) + 1)⌉ - 1

这个性质是性质4的直接推论。要让高度 h 最小，树就必须尽可能地"胖"，即节点数 n要尽可能地接近最大容量。

我们知道，节点数 n 必须小于等于高度为 h的树的最大容量。
即： n<=(m(h+1)−1)/(m−1)n<=(m^{(h+1)}-1)/(m-1)n<=(m(h+1)−1)/(m−1)
我们对这个不等式进行变形，来求解 h：

n∗(m−1)≤m(h+1)−1n*(m - 1) ≤ m^{(h+1)} - 1n∗(m−1)≤m(h+1)−1

n∗(m−1)+1≤m(h+1)n * (m - 1) + 1 ≤ m^{(h+1)}n∗(m−1)+1≤m(h+1)

现在，我们对两边取以 m 为底的对数：

logm(n(m−1)+1)≤h+1log_m(n(m-1) + 1) ≤ h + 1logm(n(m−1)+1)≤h+1

h≥logm(n(m−1)+1)−1h ≥ log_m(n(m-1) + 1) - 1h≥logm(n(m−1)+1)−1

因为高度 h 必须是整数，所以 h 的最小值就是对右边式子向上取整的结果。

它揭示了树结构最高效的地方：用对数级别的高度，存储指数级别的节点 。

举个例子，一个度为100的树（在数据库B-Tree中很常见），只需要3层的高度(h=2)，就可以存储 (100^3-1)/(100-1) ≈ 10101 个节点。这意味着从上亿条数据中查找，可能只需要4-5次操作（磁盘IO）。

这个性质是所有高效索引结构（如B树、B+树）的理论基石，它们的核心思想就是通过维持树的平衡，使其高度始终接近这个理论最小值，从而保证查询、插入和删除操作的高性能。

3、多叉树的存储

对于二叉树，我们知道可以用一个包含left和right两个指针的节点来存储。但多叉树的子节点数量不固定，我们该怎么办？

3.1、父节点表示法

最简单的方式是使用一个数组，每个元素存储其父节点在数组中的索引。根节点的父节点索引设为一个特殊值（如-1）。

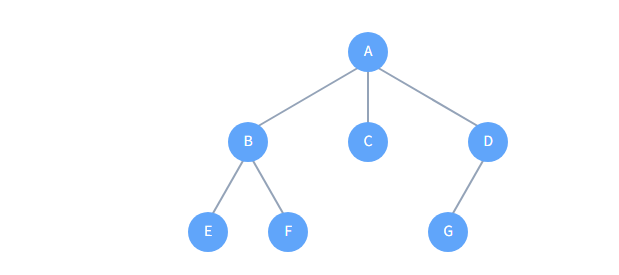
假设节点 A,B,C,D,E,F,G 分别对应索引 0-6

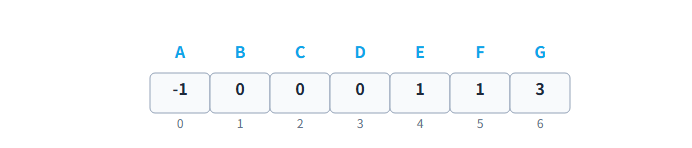
为什么这么设计？
优点：结构非常简单，寻找一个节点的父节点操作是 O(1) 的常数时间复杂度，非常快。**缺点：**致命的缺点是无法直接找到一个节点的子节点。要找到A(索引0)的所有孩子，你需要遍历整个数组，看看谁的值是0，效率极低。这在实际应用中几乎不可接受。

3.2、孩子表示法

让每个节点持有一个列表（或动态数组、链表），专门用来存放其所有子节点的引用。

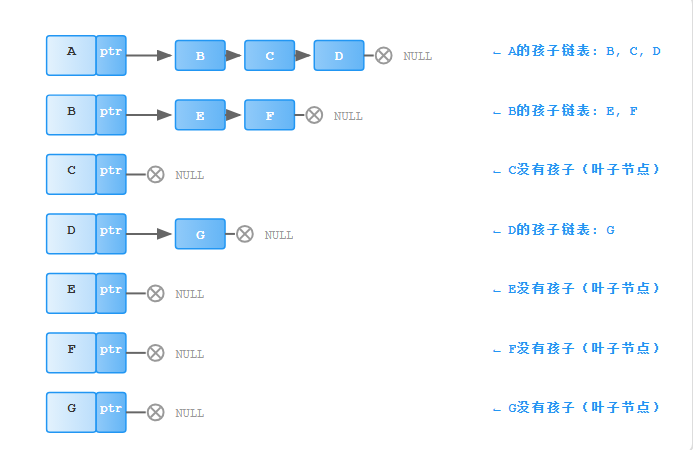
为什么这么设计？
优点： 非常直观，找一个节点的所有孩子非常方便。
缺点：

每个节点的子节点数不同，导致节点大小不一，管理内存不便。
想要访问兄弟节点（比如从B访问C）很不方便，需要先回到父节点A，再遍历A的孩子列表。

3.3、孩子兄弟表示法

这是解决多叉树存储问题的最经典、最通用 的方案。它通过一种巧妙的转换，将任何多叉树都变成一棵二叉树来存储和操作。

**核心思想：**每个节点只保存两个指针：

firstChild：指向它的第一个孩子节点。
nextSibling：指向它的下一个兄弟节点。

口诀就是："左孩子，右兄弟"。

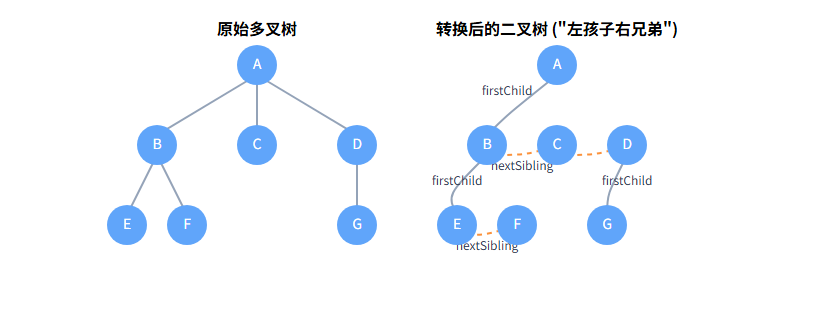
多叉树视角

A的孩子：B, C, D
B的孩子：E, F
D的孩子：G

二叉树视角

A的左孩子：B
B的左孩子：E，右孩子：C
C的右孩子：D
D的左孩子：G
E的右孩子：F

为什么要这样转换？
1. 结构统一： 无论原来的多叉树多么"张牙舞爪"，有多少分支，转换后都变成了一个结构规则 的二叉树。这意味着我们可以用统一的节点结构（一个数据域，两个指针域）来表示所有树！
2. 算法复用： 这是最重要的一点。所有为二叉树设计的精妙算法，比如各种遍历（前序、中序、后序）、查找、插入、删除等，都可以几乎不加修改地 应用到这棵转换后的二叉树上，从而间接操作了原来的多叉树。我们不需要为多叉树再发明一套全新的、复杂的算法。
3. 空间效率： 相对于孩子列表法，这种方法通常更节省空间，因为每个节点的大小是固定的。

4、多叉树的遍历

多叉树的遍历主要有两种方式：先根遍历（前序遍历） 、后根遍历（后序遍历） 和层次遍历。注意，多叉树没有严格意义上的"中序遍历"，因为一个节点的子树有多个，无法明确定义"中间"的位置。

先根遍历

规则：先访问根节点，然后依次对根节点的每棵子树进行先根遍历。

对于上图的树，遍历顺序是：A -> B -> E -> F -> C -> D -> G

后根遍历

规则：先依次对根节点的每棵子树进行后根遍历，最后再访问根节点。

对于上图的树，遍历顺序是：E -> F -> B -> C -> G -> D -> A

层次遍历

规则：从根节点开始，从上到下、从左到右，逐层访问节点。这通常需要借助一个队列来实现。

对于上图的树，遍历顺序是：A -> B -> C -> D -> E -> F -> G

遍历的等价性

当你把多叉树用"孩子兄弟法"转成二叉树后，会发现一个惊人的对应关系。这个结论非常重要，它证明了"孩子兄弟表示法"的强大之处，将不同结构的遍历操作也统一起来了。

🌳 多叉树的先根遍历 <==> 对应二叉树的前序遍历
🌳 多叉树的后根遍历 <==> 对应二叉树的中序遍历

让我们一步步地、清晰地走一遍遍历过程，来验证这个神奇的结论为什么成立。

验证1：多叉树先根遍历 vs 对应二叉树前序遍历

目标序列（多叉树先根）： A → B → E → F → C → D → G

二叉树前序遍历规则： 根 → 左 → 右

现在，我们对转换后的二叉树（左孩子-右兄弟）进行前序遍历：

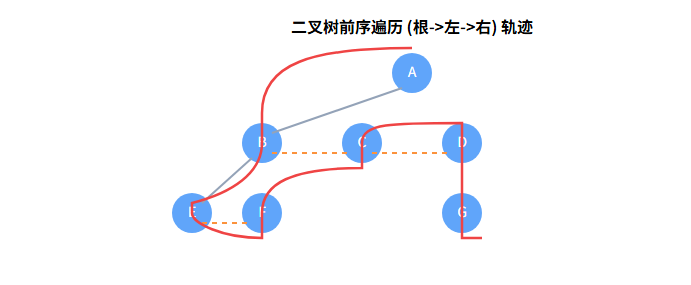
访问根 A。 (序列: A)
沿 firstChild (左) 找到 B。访问 B。(序列: A, B)
沿 B 的 firstChild (左) 找到 E。访问 E。(序列: A, B, E)
E 没有 firstChild (左)。沿 E 的 nextSibling (右) 找到 F。访问 F。(序列: A, B, E, F)
F 没有孩子和兄弟了。返回到 B。
沿 B 的 nextSibling (右) 找到 C。访问 C。(序列: A, B, E, F, C)
C 没有 firstChild (左)。沿 C 的 nextSibling (右) 找到 D。访问 D。(序列: A, B, E, F, C, D)
沿 D 的 firstChild (左) 找到 G。访问 G。(序列: A, B, E, F, C, D, G)
G 没有孩子和兄弟了。全部遍历完毕。

因为多叉树的"先根"就是先访问父节点，再依次访问它的孩子。而在二叉树中，firstChild 指针完美对应了"第一个孩子"，nextSibling 指针完美对应了"下一个孩子"。所以二叉树的前序遍历（根→左→右）的逻辑，恰好就是沿着firstChild深入，再沿着 nextSibling 平移，完美复现了多叉树的先根遍历过程。

验证2：多叉树后根遍历 vs 对应二叉树中序遍历

目标序列（多叉树后根）： E → F → B → C → G → D → A

二叉树中序遍历规则： 左 → 根 → 右

现在，我们对转换后的二叉树进行中序遍历：

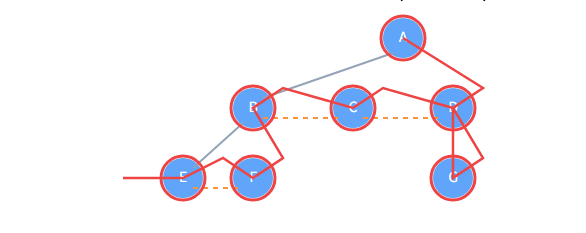
从 A 出发，一路向左(firstChild)走到底：A → B → E。
E 的左边是空。访问 E。(序列: E)
访问 E 的右边(nextSibling)，找到 F。F的左边是空，访问 F。(序列: E, F)
F 的右边是空。返回到 B。
B 的左边(E-F链)已经访问完。访问 B。(序列: E, F, B)
访问 B 的右边(nextSibling)，找到 C。
C 的左边是空。访问 C。(序列: E, F, B, C)
访问 C 的右边(nextSibling)，找到 D。
D 的左边(firstChild)是 G。G 的左边是空，访问 G。(序列: E, F, B, C, G)
G 的右边是空。返回到 D。D 的左边已访问完，访问 D。(序列: E, F, B, C, G, D)
D 的右边是空。返回到 A。
A 的左边(B-C-D链)已经访问完。访问 A。(序列: E, F, B, C, G, D, A)

多叉树的"后根"是先处理完所有子树，最后才处理根。在转换后的二叉树中，一个节点的所有子树都在它的firstChild(左)分支上。中序遍历（左→根→右）的规则要求我们必须先处理完整个左子树，才能访问根节点。这就天然地保证了"先处理完所有孩子，再处理父亲"的顺序。而处理完左子树后，访问右子树(nextSibling)，正好对应了多叉树中"处理完一个孩子的所有后代，再处理下一个兄弟"的逻辑。

5、Python代码实现多叉树

python 复制代码

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
from collections import deque


class CSNode:
    """
    孩子兄弟表示法的节点类 (Child-Sibling Node)
    """
    def __init__(self, data):
        self.data = data
        self.first_child = None  # 指向第一个孩子节点 (等价于二叉树的左孩子)
        self.next_sibling = None # 指向下一个兄弟节点 (等价于二叉树的右孩子)


class CSTree:
    """
    基于孩子兄弟表示法的多叉树类
    """
    def __init__(self, root_data=None):
        if root_data is not None:
            self.root = CSNode(root_data)
        else:
            self.root = None
    
    def print_visual(self):
        """
        可视化打印整棵树的结构
        """
        print("---------- 树结构可视化 (孩子兄弟法) ----------")
        if not self.root:
            print("空树")
            return
        
        self._print_visual_recursive(self.root)
        print("---------------------------------------------")

    def _print_visual_recursive(self, node, prefix="", is_last=True):
        if not node:
            return
            
        print(prefix + ("└── " if is_last else "├── ") + str(node.data))
        
        # 准备子节点的前缀
        child_prefix = prefix + ("    " if is_last else "│   ")
        
        # 遍历孩子-兄弟链表
        child = node.first_child
        while child:
            # 判断当前孩子是否是其父节点孩子链表中的最后一个
            is_last_child = (child.next_sibling is None)
            self._print_visual_recursive(child, child_prefix, is_last_child)
            child = child.next_sibling

    def pre_order_traversal(self):
        """
        多叉树的先根遍历。
        这等价于对其孩子兄弟表示法二叉树的【前序遍历】。
        """
        result = []
        self._pre_order_recursive(self.root, result)
        return result

    def _pre_order_recursive(self, node, result):
        if not node:
            return
        # 1. 访问根节点 (根)
        result.append(node.data)
        # 2. 递归访问孩子子树 (左)
        self._pre_order_recursive(node.first_child, result)
        # 3. 递归访问兄弟子树 (右)
        self._pre_order_recursive(node.next_sibling, result)

    def post_order_traversal(self):
        """
        多叉树的后根遍历。
        这等价于对其孩子兄弟表示法二叉树的【中序遍历】。
        """
        result = []
        self._post_order_recursive(self.root, result)
        return result

    def _post_order_recursive(self, node, result):
        if not node:
            return
        # 1. 递归访问孩子子树 (左)
        self._post_order_recursive(node.first_child, result)
        # 2. 访问根节点 (根)
        result.append(node.data)
        # 3. 递归访问兄弟子树 (右)
        self._post_order_recursive(node.next_sibling, result)

    def level_order_traversal(self):
        """
        多叉树的层次遍历。
        注意：这不等同于其二叉树形态的层次遍历。
        """
        result = []
        if not self.root:
            return result
        
        queue = deque([self.root])
        
        while queue:
            current_node = queue.popleft()
            result.append(current_node.data)
            
            # 将当前节点的所有孩子（通过兄弟链表连接）加入队列
            child = current_node.first_child
            while child:
                queue.append(child)
                child = child.next_sibling
                
        return result

# --- 主程序：构建并操作树 ---
if __name__ == "__main__":
    # 1. 构建一棵示例树，手动连接孩子和兄弟指针
    #      A
    #      ├── B
    #      │   ├── E
    #      │   └── F
    #      ├── C
    #      └── D
    #          └── G
    
    # 创建所有节点
    a = CSNode('A')
    b = CSNode('B')
    c = CSNode('C')
    d = CSNode('D')
    e = CSNode('E')
    f = CSNode('F')
    g = CSNode('G')
    
    # 创建树
    tree = CSTree()
    tree.root = a
    
    # 连接 A 的孩子: B -> C -> D
    a.first_child = b
    b.next_sibling = c
    c.next_sibling = d
    
    # 连接 B 的孩子: E -> F
    b.first_child = e
    e.next_sibling = f
    
    # 连接 D 的孩子: G
    d.first_child = g
    
    # 2. 可视化打印树
    tree.print_visual()
    
    # 3. 执行各种遍历
    print("\n先根遍历 (等价于二叉树前序):", tree.pre_order_traversal())
    print("后根遍历 (等价于二叉树中序):", tree.post_order_traversal())
    print("层次遍历 (多叉树自身逻辑):", tree.level_order_traversal())


# ---------- 树结构可视化 (孩子兄弟法) ----------
# └── A
#     ├── B
#     │   ├── E
#     │   └── F
#     ├── C
#     └── D
#         └── G
# ---------------------------------------------

# 先根遍历 (等价于二叉树前序): ['A', 'B', 'E', 'F', 'C', 'D', 'G']
# 后根遍历 (等价于二叉树中序): ['E', 'F', 'B', 'C', 'G', 'D', 'A']
# 层次遍历 (多叉树自身逻辑): ['A', 'B', 'C', 'D', 'E', 'F', 'G']

6、时间复杂度分析

对于多叉树，不同操作的时间复杂度与其具体的存储结构密切相关。我们来分析三种主要存储方案下的性能表现。

在此，我们约定：n 代表树的总节点数，h 代表树的高度，k 代表一个节点的子节点数量。

父节点表示法

查找父节点： O(1)。这是该方法唯一的优势，因为我们直接通过数组索引就能找到存储的父节点索引。
查找子节点： O(n)。为了找到一个节点的所有孩子，我们必须遍历整个数组，检查每个元素的父节点索引是否是当前节点，效率极低。

**小结：**该方法由于查找子节点效率太差，几乎只用于那些"只需要向上追溯"的特殊场景，如并查集。

孩子列表表示法

查找所有子节点： O(k)。访问节点的孩子列表是 O(1)，遍历这个列表需要 O(k) 时间。非常高效。
查找父节点： O(n)。这种结构没有直接指向父节点的指针。在最坏的情况下，为了找到任意一个节点的父节点，我们可能需要从根节点开始遍历整棵树。
遍历整棵树（先根/后根/层次）： O(n)。因为每种遍历都会确保每个节点和每条边都只被访问一次，所以总的时间复杂度与节点总数成正比。

**小结：**这是最直观的实现，对"向下"的操作（查找孩子）非常友好。但在需要频繁"向上"追溯的场景中表现不佳。

孩子兄弟表示法

在这种表示法下，多叉树的操作被巧妙地转换为了二叉树的操作。

查找第一个子节点： O(1)。直接访问 first_child 指针即可。
查找所有子节点： O(k)。需要沿着 next_sibling 链表遍历 k 次。
查找父节点： O(n)。和孩子列表法一样，没有直接的父指针，最坏情况下需要遍历全树。
查找兄弟节点： O(k)。从第一个兄弟开始，最多沿着 next_sibling 链表移动 k-1 次。
遍历整棵树（先根/后根）： O(n)。因为这等价于对一棵有 n 个节点的二叉树进行前序或中序遍历，每个节点访问一次，所以复杂度是 O(n)。

**小结：**这是综合性能和灵活性最好的方案。它不仅统一了数据结构，使得算法可以复用，而且在各种基本操作上都保持了良好的性能。虽然查找父节点是其短板，但这可以通过增加一个父指针（变为三叉链表）来优化，代价是稍高的空间复杂度。

7、总结

标准化问题： 现实世界中的树结构形态各异（多叉树），直接处理起来非常麻烦。我们需要一个标准化的模型。
找到标准模型： 二叉树结构规整，算法成熟，是理想的"标准模型"。
建立转换桥梁： "孩子兄弟表示法"就是这座桥梁。它能将任何不规则的多叉树，甚至是由多棵树组成的森林，都无损地、唯一地映射成一棵规则的二叉树。
享受统一处理的便利： 一旦转换完成，我们就可以用同一套二叉树的工具（存储结构、遍历算法等）来解决所有关于树的问题。