机器学习（二）：KNN算法简介及API介绍（分类、回归）

个人主页-爱因斯晨

文章专栏-机器学习

一、KNN算法_简介

K-近邻算法：根据你的邻居来推断你的类别

KNN算法思想：如果一个样本在特征空间中的k个最相似的样本中的大多数属于某一个类别，则该样本也属于这个类别。（分类思路）

样本相似性：样本都是属于一个任务数据集的。样本距离越近越相似

欧氏距离=对应维度差值平方和，开平方根

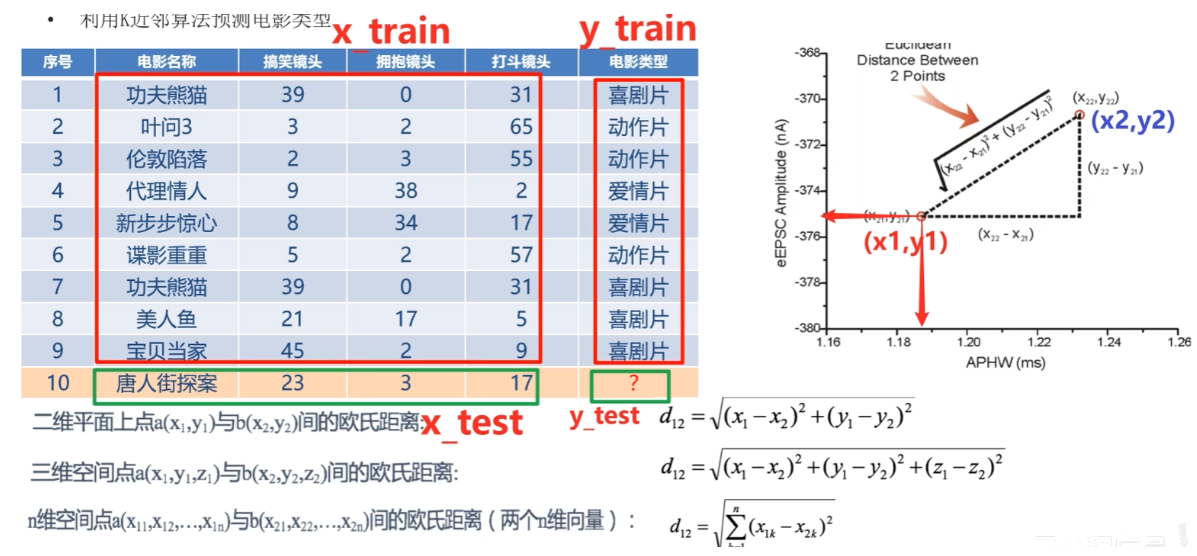
如何判断唐人街的电影类型，算点与其余例子的欧氏距离，算k=5时，找到最相近的电影类别，来决定10号电影的类别。

二、K值选择

K值过小：用较小邻域中的训练实例进行预测，容易受到异常点的影响，K值的减小就意味着整体模型变得复杂，容易发成过拟合。

K值过大：用较大领域中的训练实例进行预测，受到样本均衡的问题，且K值的增大就意味着整体的模型变得简单，欠拟合。

比如：你谈了一个男朋友，他的方方面面都会被你放大，各方面都会影响你对他的态度。如果你谈了100个，也就看个大概趋势，不会过度分析，谈一个属于过拟合，谈100个属于欠拟合。（当然，我们还是不提倡谈多个！）

举例：K=N（N为训练样本个数）无论输入实例是什么，只会按训练集中最多的类别进行预测，受到样本均衡的影响。

如何对K超参数进行调优？

需要一些方法来寻找这个最合适的K值，交叉验证、网格搜索。

什么是超参：手动传入的参数

三、KNN算法_两类流程

解决问题：分类问题（标签不连续，投票）、回归问题（标签连续，均值）

算法思想：若一个样本在特征空间k个最相似的样本大多数属于某一类别，则该样本也属于这个类别。

相似性：欧氏距离

KNN 分类 ：核心是 "多数投票"------ 找到待预测样本的 K 个最近邻，按邻域样本中最多的类别作为预测结果（比如判断鸢尾花的品种）。

KNN 回归 ：核心是 "均值 / 加权均值"------ 找到待预测样本的 K 个最近邻，用邻域样本的数值均值作为预测结果（比如预测房价、气温）。

分类流程：

复制代码

1.计算未知样本到每一个样本的距离
2.将训练样本根据距离大小升序排列
3.取出距离最近的K个训练样本
4.进行多数表决，统计K个样本中哪个类别的样本个数最多
5.将未知的样本归属到出现次数最多的类别

分类思想代码：

python 复制代码

# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, classification_report

# 1. 加载数据集（鸢尾花数据集，经典分类任务）
iris = load_iris()
X = iris.data  # 特征：花萼长度、花萼宽度、花瓣长度、花瓣宽度
y = iris.target  # 标签：0/1/2 对应3种鸢尾花品种

# 2. 划分训练集和测试集（70%训练，30%测试）
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42  # random_state固定随机数，保证结果可复现
)

# 3. 创建KNN分类器（核心：n_neighbors=5 即K=5，是最常用的默认值）
knn_classifier = KNeighborsClassifier(n_neighbors=5)

# 4. 训练模型（KNN是惰性学习，训练仅存储数据，无实际拟合过程）
knn_classifier.fit(X_train, y_train)

# 5. 预测测试集
y_pred = knn_classifier.predict(X_test)

# 6. 评估模型性能
print("=== KNN分类模型评估 ===")
print(f"分类准确率：{accuracy_score(y_test, y_pred):.2f}")
print("\n分类详细报告：")
print(classification_report(y_test, y_pred, target_names=iris.target_names))

# 7. 单个样本预测示例
sample = np.array([[5.1, 3.5, 1.4, 0.2]])  # 手动构造一个样本（对应第0类鸢尾花）
pred_label = knn_classifier.predict(sample)
print(f"\n单个样本预测结果：{iris.target_names[pred_label[0]]}")

回归流程:

复制代码

1.计算未知样本到每一个样本的距离
2.将训练样本根据距离大小升序排列
3.取出距离最近的K个训练样本
4.把这个K个样本的目标值计算其平均值
5.作为将未知的样本预测的值

回归流程思想代码：

python 复制代码

# 导入必要库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_california_housing  # 加州房价数据集（替代过时的波士顿房价）
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.preprocessing import StandardScaler  # 特征标准化（KNN对距离敏感，必须做）

# 1. 加载数据集（加州房价，回归任务：预测房价中位数）
housing = fetch_california_housing()
X = housing.data  # 特征：人口、收入、房屋年龄等8个维度
y = housing.target  # 标签：房价中位数（单位：10万美元）

# 2. 特征标准化（关键！KNN基于距离计算，特征量纲不同会影响结果）
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 3. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.3, random_state=42
)

# 4. 创建KNN回归器（K=5，权重为距离加权：近的样本权重更高）
knn_regressor = KNeighborsRegressor(n_neighbors=5, weights='distance')

# 5. 训练模型
knn_regressor.fit(X_train, y_train)

# 6. 预测测试集
y_pred = knn_regressor.predict(X_test)

# 7. 评估模型性能
print("=== KNN回归模型评估 ===")
print(f"均方误差（MSE）：{mean_squared_error(y_test, y_pred):.2f}")  # 越小越好
print(f"决定系数（R²）：{r2_score(y_test, y_pred):.2f}")  # 越接近1越好

# 8. 单个样本预测示例
sample = np.array([[8.3252, 41.0, 6.98412698, 1.02380952, 322.0, 2.55555556, 37.88, -122.23]])
# 先标准化（必须和训练集用同一scaler）
sample_scaled = scaler.transform(sample)
pred_price = knn_regressor.predict(sample_scaled)
print(f"\n单个样本房价预测值：{pred_price[0]:.2f} 10万美元")
print(f"该样本真实房价：{y[0]:.2f} 10万美元")

分类 vs 回归核心差异对比

维度	KNN 分类	KNN 回归
目标	预测离散类别（如 0/1/2、猫 / 狗）	预测连续数值（如房价、气温）
核心逻辑	多数投票（K 个邻居中最多的类别）	均值 / 加权均值（K 个邻居的数值平均）
评估指标	准确率、精确率、召回率	MSE、MAE、R²
关键预处理	可选特征标准化	必须特征标准化（距离敏感）