布隆过滤器详解：原理、实现与应用

复制代码

感谢阅读！❤️
如果这篇文章对你有帮助，欢迎 **点赞** 👍 和 **关注** ⭐，获取更多实用技巧和干货内容！你的支持是我持续创作的动力！
**关注我，不错过每一篇精彩内容！**

布隆过滤器 是Burton Howard Bloom在1970年提出的一种空间高效的概率型数据结构，核心作用是快速判断一个元素是否存在于一个集合中。它的特点是空间占用极小、查询速度极快，但存在一定的误判率，且不支持删除操作，适用于"海量数据下的快速存在性检测，且能容忍轻微误判"的场景。

一、实现原理

布隆过滤器的底层核心是一个长度为 m 的二进制位数组 + k 个相互独立的哈希函数，所有操作均围绕位数组和哈希函数展开，分别为初始化 、添加元素 、查询元素三个核心步骤。

初始化

创建一个全为0的二进制位数组，长度为 m ，同时选定 k 个独立的哈希函数，记作 h a s h 1 ( ) hash_1() hash1(), h a s h 2 ( ) hash_2() hash2(), ..., h a s h k ( ) hash_k() hashk()，每一个哈希函数能将任意输入的元素映射为 0 ~ m-1范围内的一个整数索引。
添加元素

将 n 个元素添加到布隆过滤器中。当向布隆过滤器中添加元素 x x x 时，执行以下操作:
1. 将元素 x x x 依次传入 k 个哈希函数，得到 k 个哈希值： h 1 = h a s h 1 ( x ) , h 2 = h a s h 2 ( x ) , . . . , h k = h a s h k ( x ) h_1=hash_1(x),h_2=hash_2(x),...,h_k=hash_k(x) h1=hash1(x),h2=hash2(x),...,hk=hashk(x)
2. 将二进制位数组中，索引为 h 1 , h 2 , . . . , h k h_1,h_2,...,h_k h1,h2,...,hk的位置由0变为1（若以为1，则保持不变）。
3. 将 第1步 和 第2步 骤重复 n 次，把 n 个元素添加到布隆过滤器中。
查询元素

当判断元素 y y y是否存在于数组(布隆过滤器)中，执行以下操作：
1. 将元素 y y y 依次传入 k 个哈希函数，得到 k 个哈希值： h 1 ′ = h a s h 1 ( y ) , h 2 ′ = h a s h 2 ( y ) , . . . , h k ′ = h a s h k ( y ) h'_1=hash_1(y),h'_2=hash_2(y),...,h'_k=hash_k(y) h1′=hash1(y),h2′=hash2(y),...,hk′=hashk(y)
2. 检查位数组中所有索引为 h 1 ′ , h 2 ′ , . . . , h k ′ h'_1,h'_2,...,h'_k h1′,h2′,...,hk′的值：
  - 如有任意一个位置为0，说明元素 y y y一定不存在于数组(布隆过滤器)中。因为如果添加过的元素，该位置必然被置为1
  - 若所有位置均为1，说明元素 y y y可能存在在数组(布隆过滤器)中。存在误判，因为不存在的元素的哈希值可能恰好覆盖了这些位置
误判原因：不同元素经过k个哈希函数，可能生成完全相同的k个索引，导致位数组的相同位置被置为1，此时查询未添加过的元素会被误判为"存在"

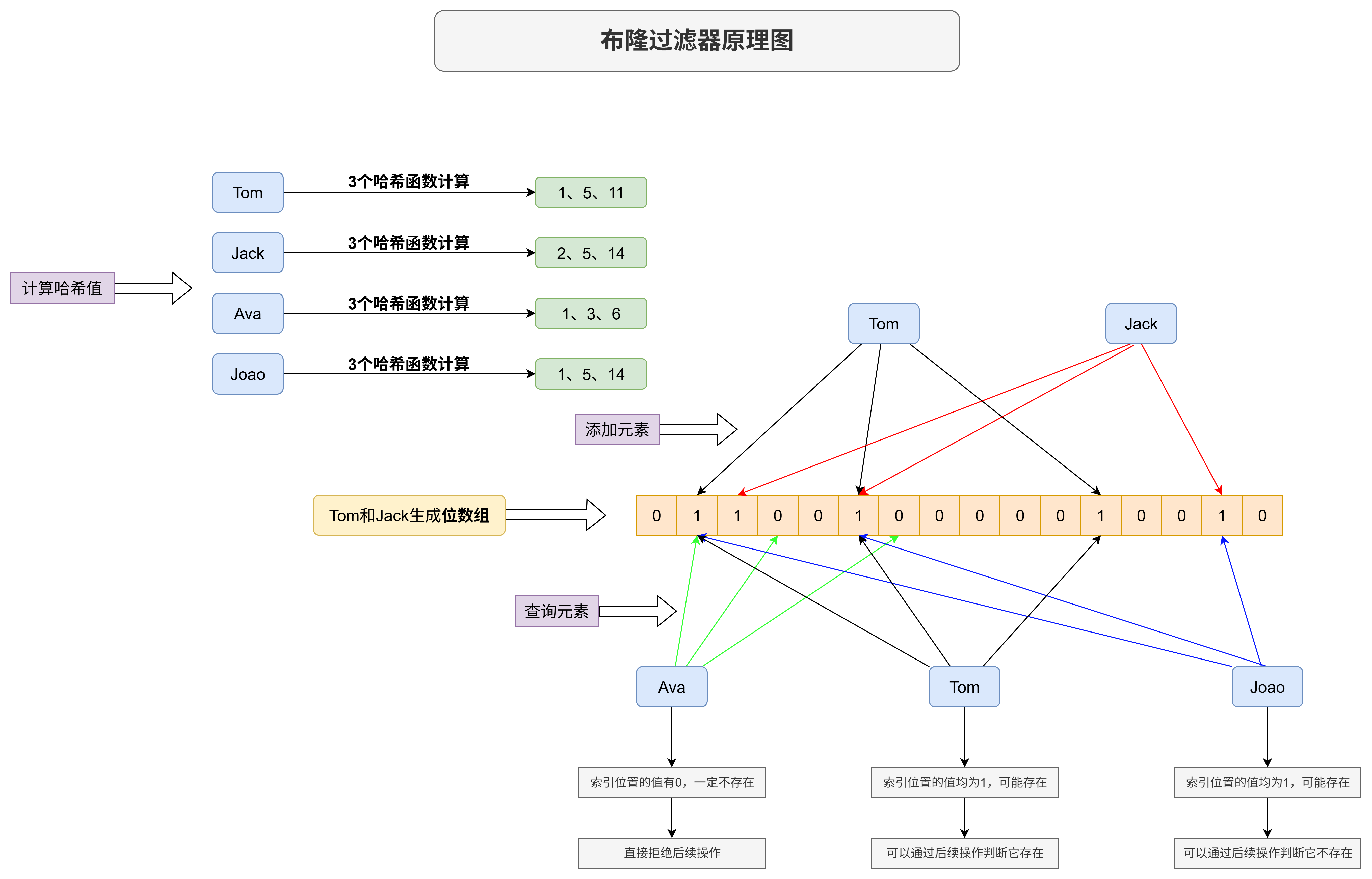
🧮 示例:

假设位数组长度为16，哈希函数个数为3个，插入元素"Tom" 和 "Jack"，然后查询"Ava"、"Tom"和"Joao"。过程如下

初始化位数组：[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
插入"Tom" → 3个哈希函数计算得到位置1、5、11 → 位数组变为：[0,1,0,0,0,1,0,0,0,0,0,1,0,0,0,0]
插入"Jack" → 3个哈希函数计算得到位置2、5、14 → 位数组变为：[0,1,1,0,0,1,0,0,0,0,0,1,0,0,1,0]
查询"Ava" → 3个哈希函数计算得到位置1、3、6 → 检查索引为1、3、6位置的值，其中2位为 0 → "Ava"绝对不存在
查询"Tom"→ 3个哈希函数计算得到位置1、5、11 → 检查索引为1、5、11位置的值，均为 1 → "Tom"可能存在
查询"Joao"→ 3个哈希函数计算得到位置1、5、14 → 检查索引为1、5、14位置的值，均为 1 → "Joao"可能存在(误判)

二、关键参数

布隆过滤器的误判率p由三个核心参数决定：位数组长度m、哈希函数个数k、预期插入元素数量n。三者相互关联，通过数学公式可计算最优参数。

所需位数组长度： m = − n ln ⁡ p ( ln ⁡ 2 ) 2 m = -\dfrac{n \ln p}{(\ln 2)^2} m=−(ln2)2nlnp
最优哈希函数个数： k = m × l n 2 n = − l n p ln ⁡ 2 k = \dfrac{m×ln 2}{n} = -\dfrac{ln p}{\ln 2} k=nm×ln2=−ln2lnp
误判率： p ≈ ( 1 − e − k n / m ) k p \approx \left(1 - e^{-kn/m}\right)^k p≈(1−e−kn/m)k

通常业务：给定预期插入元素数量n 和能容忍多大误判率p，来确定需要多大空间m和几个哈希函数k

🧮 示例:

假设你要插入 100 万个元素 （ n = 10 6 n = 10^6 n=106），希望误判率不超过 1% （ p = 0.01 p = 0.01 p=0.01）：

计算 m m m：
m = − 10 6 ⋅ ln ⁡ ( 0.01 ) ( ln ⁡ 2 ) 2 ≈ 10 6 ⋅ 4.605 0.48045 ≈ 9.59 × 10 6 bits ≈ 1.15 MB m = -\frac{10^6 \cdot \ln(0.01)}{(\ln 2)^2} \approx \frac{10^6 \cdot 4.605}{0.48045} \approx 9.59 \times 10^6 \text{ bits} \approx 1.15 \text{ MB} m=−(ln2)2106⋅ln(0.01)≈0.48045106⋅4.605≈9.59×106 bits≈1.15 MB
计算 k k k：
k = − ln ⁡ ( 0.01 ) ln ⁡ 2 ≈ 4.605 0.693 ≈ 6.64 ⇒ 取整为 7 k = -\frac{\ln(0.01)}{\ln 2} \approx \frac{4.605}{0.693} \approx 6.64 \Rightarrow \text{取整为 } 7 k=−ln2ln(0.01)≈0.6934.605≈6.64⇒取整为 7

所以：用 约 959 万 bit（≈1.15 MB） 的位数组，配合 7 个哈希函数 ，即可在插入 100 万项时保持 <1% 误判率。

三、核心特点

极高的空间效率 ：相比哈希表等传统数据结构，布隆过滤器能节省90%以上内存，存储一亿元素（误判率1%）仅需约114MB空间。
极速的查询性能 ：插入和查询的时间复杂度均为O(k)，接近常数时间。（k为哈希函数个数，通常取3~10）
概率型判断结果 ：仅支持"可能存在"和"绝不存在"两种结论。存在假阳性（误判不存在的元素为存在），但绝无假阴性（不会漏判已存在元素）
- 可能存在：不存在的元素，布隆过滤器可能判断该元素为存在。
- 绝不存在：布隆过滤器判断某个元素不存在，则该元素一定是不存在的。
不支持删除操作 ：传统布隆过滤器无法删除元素，重置位数组会影响其他元素的判断，需通过变种结构解决。

四、Java实现布隆过滤器

实现代码：

Java 复制代码

package com.aill.aspect;

import java.util.BitSet;

/**
 * 基础布隆过滤器实现
 * expectedElements 预期插入元素数量
 * falsePositiveRate 目标误判率
 */
public class SimpleBloomFilter {
    private final BitSet bitSet;
    private final int bitSetSize; // 位数组长度
    private final int hashFunctionCount; // 哈希函数个数

    public SimpleBloomFilter(int expectedElements, double falsePositiveRate) {
        // 计算最优参数
        this.bitSetSize = optimalBitSetSize(expectedElements, falsePositiveRate);
        this.hashFunctionCount = optimalHashFunctionCount(expectedElements, bitSetSize);
        this.bitSet = new BitSet(bitSetSize);
        System.out.printf("初始化完成：位数组大小=%d，哈希函数个数=%d，目标误判率=%.4f%%%n",
                bitSetSize, hashFunctionCount, falsePositiveRate * 100);
    }

    // 添加元素
    public void add(String element) {
        Long[] hashes = getHashes(element);
        for (Long hash : hashes) {
            // 哈希值转为正数后取模，避免负索引
            bitSet.set(Math.abs(hash.intValue() % bitSetSize));
        }
    }

    // 检查元素是否可能存在
    public boolean mightContain(String element) {
        Long[] hashes = getHashes(element);
        for (Long hash : hashes) {
            int index = Math.abs(hash.intValue() % bitSetSize);
            if (!bitSet.get(index)) {
                return false; // 绝对不存在
            }
        }
        return true; // 可能存在
    }

    // 生成多个哈希值（基于双重哈希法，使用Long数组存储）
    private Long[] getHashes(String element) {
        Long[] result = new Long[hashFunctionCount];
        // 先获取基础哈希值，转为Long避免int溢出
        Long hash1 = (long) element.hashCode();
        Long hash2 = (hash1 >>> 16); // 高位哈希值，保持Long类型
        for (int i = 0; i < hashFunctionCount; i++) {
            Long combinedHash = hash1 + i * hash2;
            result[i] = combinedHash;
        }
        return result;
    }

    // 计算最优位数组大小
    private int optimalBitSetSize(int n, double p) {
        return (int) (-n * Math.log(p) / Math.pow(Math.log(2), 2));
    }

    // 计算最优哈希函数个数
    private int optimalHashFunctionCount(int n, int m) {
        return Math.max(1, (int) (m / n * Math.log(2)));
    }
}

测试代码：