论文精读第七期：告别昂贵的人工标注！Math-Shepherd：如何用“零成本”自动化过程监督，让大模型数学能力暴涨？

大模型做数学题总是"一步错，步步错"？大家都知道"过程奖励模型（PRM）"效果好，但动辄几十万条的人工标注数据实在太贵了。 今天这篇博客将带你深度拆解北大与 DeepSeek 联合推出的 Math-Shepherd。它不仅提出了一种无需人类介入、基于蒙特卡洛思想的自动化数据构造方法，更在 GSM8K 和 MATH 榜单上全面碾压了传统方法。这不仅是数学推理的胜利，更是数据工程的一次教科书级示范。无论你是想复现 SOTA 效果，还是想寻找低成本提升模型逻辑能力的方案，这篇文章都不容错过。

论文下载地址：https://aclanthology.org/2024.acl-long.510.pdf

第一步：宏观背景与痛点

1. 痛点引入：为什么现在的 AI 做数学题还不够好？

虽然现在的 LLM（如 GPT-4, Llama 等）已经很强了，但在做复杂的多步骤数学题时，它们经常"翻车"。

"一步错，步步错"的问题： 数学题逻辑链条很长。模型可能第一步写对了，第二步一个小计算失误，后面十步写得再天花乱坠，最终答案也是错的。

目前的解决方案（监督）： 为了教 AI 避免错误，我们需要通过奖励模型（Reward Model）给它反馈。主要有两种流派：

流派 A：只看结果（ORM - Outcome Reward Model）： 等 AI 写完全部过程，只看最后答案对不对。这很容易获取数据（只要有答案就行），但反馈太粗糙。就像老师只给你打个X，不告诉你哪一步错了，AI 很难学到精髓 。

流派 B：盯着过程（PRM - Process Reward Model）： 老师盯着 AI 的每一步，第一步对了给糖吃，第二步错了打手板。这种方法效果最好，因为反馈精准 。

真正的痛点（The Bottleneck）： 流派 B（盯着过程）太贵了, 要训练这样的模型，以前必须依靠人类专家去给成千上万道题的每一个步骤进行人工标注（好/坏/中立）。这既费钱、又费时、还很难大规模扩展 。

这就导致了一个僵局： 我们知道"过程监督"效果好，但我们要不起那么多人工标注的数据。

2. 直觉（Intuition）：如何不花钱请老师，也能知道这一步走没走对？

这篇论文的核心直觉来自于一个很聪明的想法：利用"未来"来推断"现在"（灵感来源于蒙特卡洛树搜索 MCTS）。

想象你在走一个巨大的迷宫（做一道数学题）：

以前的做法（人工标注）： 你每走一步，都要停下来问旁边的向导（人类专家）："嘿，我这一步走对了吗？"向导说对，你才继续。这需要很多向导，很贵。

Math-Shepherd 的做法（自动推断）： 没有向导。当你走到一个路口，迈出一步（Step X）后，系统会立刻派出 10 个"分身"（让模型自动补全后续步骤）。

补全：给定问题和一个中间步骤，使用微调后的LLM作为"补全器"，从该步骤解码多个后续推理路径（如N=8）。

如果这 10 个分身里，有 8 个最后都走到了正确的终点（算出了正确答案），那么系统就反推："看来刚才迈出的那一步（Step X）大概率是正确的路。"

如果这 10 个分身全部掉进了坑里（答案全错），系统就反推："刚才那一步（Step X）肯定走错了。"

基于解码答案的正确性，通过硬估计（HE，只要任一路径答案正确则标记为1）或软估计（SE，计算正确路径比例）为步骤分配标签。

通过这种方式，不需要人类介入，只要有最终的标准答案，我们就能自动给中间的每一步打分

第二步：核心思想概览

1. 整体架构图：Math-Shepherd Pipeline

这就好比一个"倒推验证工厂"。请看下图的逻辑流（基于原论文 Figure 1 ）：

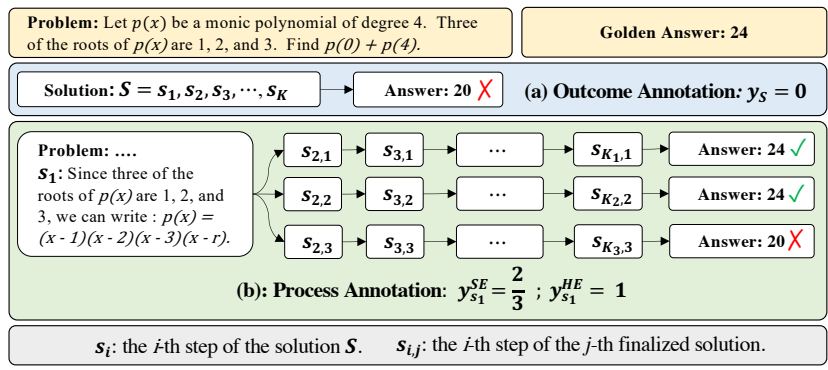
输入 (Input)：

• 一个数学问题（Problem）。

• 该问题的正确标准答案（Golden Answer，比如 "24"）。

• 注意：不需要人工标注的详细解题步骤，只要有这一对"问题+答案"即可。

处理流程 (The Pipeline)：

1. 切片 (Slice)： 模型生成一个解题步骤（例如 Step ）。

2. 分身模拟 (Rollout / Completion)： 从这一步 开始，让一个辅助模型（Completer）自动把剩下的步骤走完。重复走 次（比如 8 次），生成 N条完整的解题路径。

3. 结果校验 (Check)： 检查这 条路径最终得出的答案，是否等于标准答案（Golden Answer）。

4. 打分 (Label)： 如果有高比例的路径算出了正确答案，说明 这一步很有潜力，打高分（Label = 1 或高概率）。如果大部分路径都算错了，说明 这一步大概率是胡扯，打低分（Label = 0 或低概率）。

输出 (Output)：

构建好的一套过程级监督数据集 (Process-wise supervision data) 。

最终训练出的 Math-Shepherd 模型（即 PRM），它学会了看一眼中间步骤就能判断好坏。

这一架构的巧妙之处在于将步骤质量定义为"推导出正确答案的潜力"，无需人工介入即可生成细粒度标签。

2. 关键创新点（Key Insight）：把"未来"的确定性传导给"当下"

作者并没有发明新的损失函数，也没有设计复杂的全新神经网络模块。他们的核心创新在于数据构建的逻辑 ，灵感来源于 蒙特卡洛树搜索 (Monte Carlo Tree Search, MCTS) 的思想 。

巧妙之处：

通常我们要判断"步骤 A"对不对，需要专家懂逻辑。但作者认为，不需要懂逻辑，只需要看结果。"条条大路通罗马"，如果你这一步走完，后面随便走走都能到罗马（正确答案），那你这一步就是好步。

具体实现：

硬估计 (Hard Estimation)： 只要 N 条路径里有一条能算出对的答案，就给这一步标为"好"（Label = 1）。作者发现这种简单粗暴的方法反而效果很好 。

软估计 (Soft Estimation)： 按照算出正确答案的比例给分（例如 8 条里有 6 条对，得分 0.75）。

3. 与前人对比：突破PRM的标注瓶颈

我们可以通过对比来看 Math-Shepherd 的独特站位：

方法	核心逻辑	数据来源	缺点	Math-Shepherd 的优势
ORM (Outcome Reward Model) 10	等全写完，只看最后答案对不对。	自动生成 (Cheap)	反馈太迟钝，不知道哪一步错了 。	颗粒度更细： 给每一步都打分，能精准定位错误 。
Manual PRM (人工过程监督) 13	专家盯着每一步打分 (Good/Bad)。	人工标注 (Expensive)	极贵，难扩展，甚至需要 GPT-4 这种昂贵的老师 。	零人工成本： 完全自动化，用开源模型自己就能生成数据 。
Math-Shepherd (本文)	看这一步能不能推导出正确答案。	自动生成 (Auto)	需要一定的推理计算资源来生成路径。	高质且量大： 数据集比人工标注的大4倍，且效果更好 。

总结这篇论文的"高光时刻"： 作者证明了，利用正确答案作为"锚点"，通过自动化采样反推中间步骤的质量，不仅可行，而且训练出来的奖励模型（PRM）比仅靠结果监督（ORM）强得多，甚至在某些指标上超过了昂贵的人工标注数据 。

第三步：技术细节拆解

这篇论文在工程实现上其实由三个严密的阶段组成：数据构造（造路） -> 模型训练（学路） -> 推理与强化（走路）。

1. 阶段一：自动过程标注算法（The Automatic Process Annotation）

这是论文最大的贡献。传统的做法是让 GPT-4 打分，或者让人打分。这里完全靠算法自举。

算法伪代码逻辑（基于 Monte Carlo Tree Search 思想）：

假设有一道数学题 ，标准答案是 （比如 42）。

模型尝试生成了一个解题步骤序列 ，但最终答案算错了。我们想知道：到底哪一步开始错的？

我们遍历每一步 ：

1.截断（Truncate）： 保留前 步 作为前缀（Prefix）。

2.蒙特卡洛模拟（Monte Carlo Rollout / Completion）：

• 保持前缀不变，让一个补全模型（Completer Model） 接着往下写。

• 重复写 次（论文中 ）。

• 得到 个完整的解题路径和 个最终答案 。

3.计算"步骤质量"标签（Label Assignment）：

硬估计（Hard Estimation, HE） ------ 这是论文推荐的默认设置 。 只要这 个答案里，有一个 等于标准答案 ，这一步 就是"好步骤"（Label = 1）。

深度解析： 为什么要这么宽容？因为 N 毕竟有限（只试了8次）。如果这一步其实是对的，但补全模型运气不好，8次都没算对，我们不能冤枉这一步。只要有一次对了，就证明这一步保留了通向真理的可能性（Potential）。

软估计（Soft Estimation, SE）： 计算正确率。如果8次里有4次对，标签就是 0.5。

数据规模细节： 通过这种方法，作者构建了庞大的训练集：

• GSM8K: 约 17 万条数据。

• MATH: 约 27 万条数据。

• 对比： 这个数据量是之前著名的 PRM800K（人工+GPT-4标注）的 4倍

2. 阶段二：过程奖励模型（PRM）的训练细节

拿到数据 后，如何训练 Math-Shepherd？

在这一阶段，我们的目标是训练一个能看懂数学步骤的"判卷老师"。

1. 核心设计：把"回归问题"变成"语言模型问题"

通常，训练 Reward Model（RM）需要给 LLM 加一个标量回归头（Scalar Head），输出一个浮点数。但这意味着要修改模型架构，加载权重时也很麻烦。

Math-Shepherd 采用了一种"Token 映射法"，直接利用 LLM 原生的 Next Token Prediction 能力

标签映射：

定义两个特殊的 Token 来代表类别：

• （例如 "Yes" 或 "+"）：代表该步骤有潜力（Label = 1）。

• （例如 "No" 或 "-"）：代表该步骤无潜力（Label = 0）。

输入构造： 将问题、步骤和标签拼接成一段文本。

• 格式： Problem + Step_1 + [Label_Token] + Step_2 + [Label_Token] ...

• 注意： 训练时，只对 [Label_Token] 的位置计算 Loss，中间的解题文本（Step text）只作为 Context，不计算 Loss。

2. 训练目标函数 (The Loss Function)

由于使用了 Hard Estimation（硬标签），训练就变成了标准的交叉熵损失（Cross Entropy）。

对于第 个步骤，模型预测下一个 Token 是 的概率为：

Loss 公式：

• ：模型读完第 步后的隐层状态（Hidden State）。

• ：我们在阶段一生成的硬标签（0 或 1）。

• 物理含义： 强迫模型在读完一个步骤后，预测下一个词是"Yes"还是"No"。如果是"Yes"的概率高，说明这一步质量好。

3. 为什么不使用软标签（Soft Estimation）？

虽然作者提出了软标签，但在实际训练 PRM 时，作者明确指出"为了方便（For the sake of convenience）"使用了硬标签版本 。

• 原因： 软标签需要回归损失（MSE）或者特殊的分布对齐，而硬标签可以直接复用所有现成的 LLM 训练代码（如 HuggingFace Trainer），不需要改一行底层代码。

3. 阶段三：推理与强化学习（Verification & RL）

模型训练好了，怎么用？这里有两个完全不同的应用场景。

场景 A：验证器（Verifier / Reranking）------ 也就是"做题模式" 模型生成 256 个候选答案，Math-Shepherd 负责挑出最好的一个。

评分公式（The Weakest Link Principle）：

深度解析： 为什么用 min（最小值）而不是 average（平均值）或 product（乘积）？

• 逻辑链的脆弱性： 数学推理是严密的逻辑链。如果步骤 1-9 都非常完美（得分0.99），但步骤 10 犯了一个严重错误（得分0.01），整个推理就崩塌了。

• 如果用平均分，(0.99 * 9 + 0.01) / 10 = 0.89，分数依然很高，模型会误判。

• 如果用最小值，得分就是 0.01，直接淘汰。这非常符合数学的特性。

场景 B：强化学习（Step-by-Step PPO）------ 也就是"刷题提分模式" 这是为了让模型自己变强，不再依赖 Math-Shepherd 辅助。

传统 PPO (Outcome RL)： 只有等到模型写完 EOS（结束符），才给一个奖励。

缺点： 奖励太稀疏，模型不知道中间哪里做对了。

Math-Shepherd PPO (Process RL)：

密集奖励（Dense Reward）。 每生成一个步骤结束符（比如换行符），立刻计算该步骤的 PRM 得分作为奖励。

优点： 实时反馈。模型写第一步时就知道写得好不好，梯度更新更准确。

论文结果显示，Process RL 把 Mistral-7B 在 GSM8K 上的准确率从 77.9% 提升到了 84.1% 。 根本原因： 它缩短了反馈回路。模型写错第一步时，马上收到一个低分（比如 0.1），PPO 算法会立刻惩罚产生这一步的概率，而不需要等到整道题做完。

第四步：实验结果

核心战绩（SOTA Results）：

作者在两个最权威的数学推理基准数据集上进行了测试：GSM8K （小学数学，相对简单）和 MATH（高难度竞赛数学）。

A. 验证器模式（Verification）------ 谁是最佳判卷人？ 对比以下三种策略的准确率（Best-of-N, N=256）：

1. Self-Consistency (SC): 少数服从多数（基准线）。

2. ORM: 结果奖励模型。

3. Math-Shepherd (PRM): 本文提出的过程奖励模型。

模型 (Generator)	数据集	Self-Consistency	ORM	Math-Shepherd (Ours)	提升幅度
DeepSeek-67B	GSM8K	88.2%	92.6%	93.3%	+5.1%
DeepSeek-67B	MATH	45.4%	45.3%	48.1%	+2.7%
Mistral-7B	MATH	35.1%	36.4%	38.3%	+3.2%

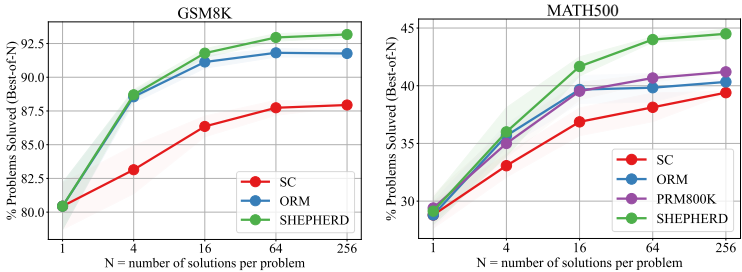
B. 强化学习模式（RL）------ 谁是最佳教练？ 使用 Mistral-7B 作为学生模型，分别用 ORM 和 Math-Shepherd 进行 PPO 训练。

• 基座模型 (Mistral-7B): 28.6% (MATH 准确率)

• + Outcome RL (传统结果奖励): 31.3%

• + Process RL (Math-Shepherd): 33.0%

• 关键结论： 用 Math-Shepherd 进行"步步为营"的训练，提分效果显著优于只看结果的传统训练。从 28.6% 提升到 33.0%，这在 MATH 这种高难度榜单上是巨大的飞跃 。

第五步：总结与升华（The "Takeaway"）

1. 优缺点分析（Pros & Cons）

没有任何一篇论文是完美的，Math-Shepherd 也不例外。

优点（The Good）：

• 零人工成本（Zero Human Labor）： 这是它最大的贡献。打破了"只有花大钱请人标注，才能训练过程奖励模型（PRM）"的刻板印象 。

• 效果拔群（High Performance）： 不仅在 GSM8K 和 MATH 上击败了传统的 ORM，甚至超越了之前依靠 GPT-4 生成的 PRM800K 数据集 2。

• 数据效率高（Data Efficient）： 仅需传统方法 1/16 的数据量就能达到同等效果，说明"过程反馈"的信息密度极高 3。

局限性（The Bad）：

• 算力换人工（Computational Cost）： 虽然省了人工费，费了更多的算力资源。为了给一个步骤打标签，模型需要重复推演 N 次（文中 N=8）。如果你有百万条数据，这需要的 GPU 推理算力是非常巨大的 。

• 标签噪声（Noisy Labels）： 自动标注依然存在"假阳性"。有时候模型推理逻辑完全错了，但碰巧算对了答案（例如错上加错等于对）。虽然硬估计（Hard Estimation）能缓解，但无法根除这种噪声 。

• 依赖"老师"水平（Dependency）： 数据质量高度依赖"补全模型"的能力。如果模型本身太弱，甚至无法推导出正确答案，它就没法给自己生成高质量的训练数据 。

2. 未来展望：这不仅仅是做数学题

Math-Shepherd 的思想（MCTS + 自动过程监督）完全可以迁移到其他领域：

• 代码生成（Code Generation）： 代码是天然适合这个框架的领域。

  • Math-Shepherd: 看推导出的答案对不对。

  • Code-Shepherd: 看生成的代码能不能通过单元测试（Unit Tests）。 我们可以用同样的方法训练一个 Code PRM，让 AI 写代码时每写一行都知道自己有没有写 Bug。

• Agent 规划（Agent Planning）： 当 AI Agent 执行复杂任务（比如订机票）时，可以通过模拟执行结果来反推当前决策的质量，实现自我修正。

• 对我们工作的启发： 不要迷信"大数据"或"纯人工标注"。高质量的自动反馈信号（High-quality automated feedback） 才是提升模型逻辑能力的关键。利用结果（Ground Truth）去反推过程，是一条极其高效的路径。

3. Key Takeaway

如果关于这篇论文您只能记住一件事，请记住这个：

"结果好，过程不一定对；但通过模拟无数个未来，我们可以反推当下的每一步是否通向真理。"

至此，关于 Math-Shepherd 的完整深度讲解就结束了。 从痛点（人工太贵） ，到原理（自动补全反推） ，再到实战（PRM与PPO训练） ，最后到升华（过程监督的未来）。