GESP C++五级-202406

选择题

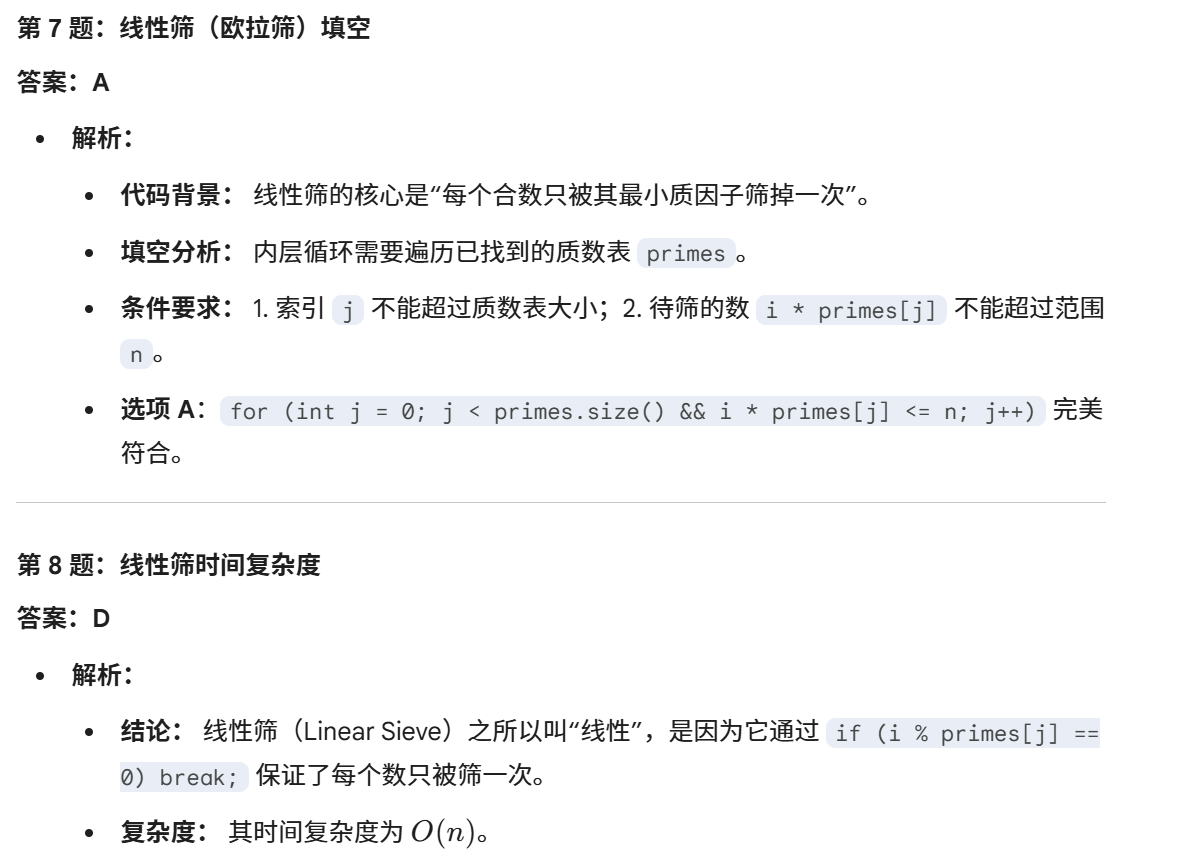
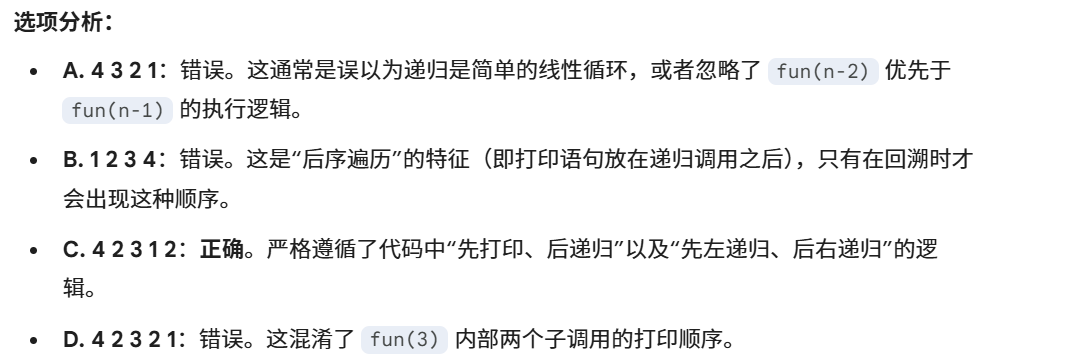
判断题

编程题

1. 黑白格

C++代码实现

cpp 复制代码

#include <iostream>
#include <string>
#include <algorithm>

using namespace std;

// 根据数据范围 n, m <= 100，给定略大的常量
const int N = 110;
const int INF = 1e9;

int n, m, k;
int s[N][N]; // s[i][j] 表示第 j 列前 i 行黑格子的数量（列前缀和）

int main() {
    // 优化输入效率（可选）
    ios::sync_with_stdio(false);
    cin.tie(0);

    if (!(cin >> n >> m >> k)) return 0;

    for (int i = 1; i <= n; i++) {
        string row;
        cin >> row;
        for (int j = 1; j <= m; j++) {
            int val = (row[j - 1] == '1' ? 1 : 0);
            s[i][j] = s[i - 1][j] + val; // 预处理列前缀和
        }
    }

    int ans = INF;
    bool found = false;

    // 枚举子矩形的上边界 i 和下边界 j
    for (int i = 1; i <= n; i++) {
        for (int j = i; j <= n; j++) {
            int height = j - i + 1;
            
            // 使用双指针（滑动窗口）维护列边界 l 和 r
            int sum = 0;
            for (int l = 1, r = 1; r <= m; r++) {
                sum += (s[j][r] - s[i - 1][r]); // 累加当前列在 [i, j] 行区间内的黑格子数

                // 当黑格子总数 >= k 时，尝试收缩左边界 l 以减小面积
                while (sum >= k) {
                    found = true;
                    ans = min(ans, height * (r - l + 1));
                    sum -= (s[j][l] - s[i - 1][l]);
                    l++;
                }
            }
        }
    }

    if (!found) cout << 0 << endl;
    else cout << ans << endl;

    return 0;
}

2. 小杨的幸运数字

C++代码实现

cpp 复制代码

#include <iostream>

using namespace std;

const int N = 1000010;

// cnt[i] 存储数字 i 的不同质因子个数
int cnt[N];
int n;

// 类似埃氏筛的预处理函数
void precompute() {
    for (int i = 2; i < N; i++) {
        // 如果 cnt[i] 仍为 0，说明 i 是一个质数
        if (cnt[i] == 0) {
            // 将该质数的所有倍数的质因子计数加 1
            for (int j = i; j < N; j += i) {
                cnt[j]++;
            }
        }
    }
}

int main() {
    // 优化输入输出效率
    ios::sync_with_stdio(false);
    cin.tie(0);

    // 执行预处理
    precompute();

    if (!(cin >> n)) return 0;

    while (n--) {
        int a;
        cin >> a;
        // 如果不同质因子个数恰好为 2，输出 1，否则输出 0
        if (cnt[a] == 2) {
            cout << 1 << "\n";
        } else {
            cout << 0 << "\n";
        }
    }

    return 0;
}

C++代码实现

cpp 复制代码

#include <iostream>

using namespace std;

const int N = 1000010;

// cnt[i] 存储数字 i 的不同质因子个数
int cnt[N];
int n;

// 类似埃氏筛的预处理函数
void precompute() {
    for (int i = 2; i < N; i++) {
        // 如果 cnt[i] 仍为 0，说明 i 是一个质数
        if (cnt[i] == 0) {
            // 将该质数的所有倍数的质因子计数加 1
            for (int j = i; j < N; j += i) {
                cnt[j]++;
            }
        }
    }
}

int main() {
    // 优化输入输出效率
    ios::sync_with_stdio(false);
    cin.tie(0);

    // 执行预处理
    precompute();

    if (!(cin >> n)) return 0;

    while (n--) {
        int a;
        cin >> a;
        // 如果不同质因子个数恰好为 2，输出 1，否则输出 0
        if (cnt[a] == 2) {
            cout << 1 << "\n";
        } else {
            cout << 0 << "\n";
        }
    }

    return 0;
}