目录
前言
本文主要介绍力扣100题相同的树和101题对称二叉树的解题思路和代码
这两道题是递归算法用于二叉树的入门算法,对于理解递归过程很有帮助
相同的树
题目描述
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例
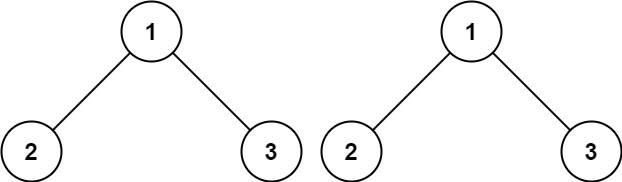
输入: p = [1,2,3], q = [1,2,3]
**输出:**true
解题思路
利用递归思路求解,在思考递归过程时只用思考本层和紧挨着下一层的情况,再往下无论有多少层都是一样的处理逻辑,很容易写出递归代码
对于本题来说,要判断是否是同样的树,只需判断当前对应树节点(如图中的两个根节点进行比较)的值是否相同,以及左子树和右子树是否相同,而判断左子树和右子树是否相同时所使用的逻辑是相同的,即反复调用相同的函数,这就是递归的思想
使用递归算法很重要的一点是终止条件,本题的终止条件是当前对应树节点出现空的情况,表示已经遍历到头了,结合代码更容易理解
代码
python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def isSameTree(self, p: Optional[TreeNode], q: Optional[TreeNode]) -> bool:
if p is None or q is None:
return p is q # 必须都是 None才是true
return p.val == q.val and self.isSameTree(p.left, q.left) and self.isSameTree(p.right, q.right)对称二叉树
题目描述
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例
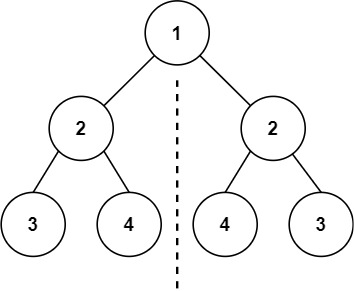
输入: root = [1,2,2,3,4,4,3]
**输出:**true
解题思路
本题仍然可以用递归算法求解,问题可这样拆分:
先把根节点单独拿出来,从图中值为 2 的两个节点开始,后面的过程就可以递归了:每次递归都先判断左边节点的值是否与右边节点的值相同,且左边节点的左子树是否与右边节点的右子树镜像,左边节点的右子树是否与右边节点的左子树镜像,而判断左右子树镜像的逻辑与上述判断过程相同(先判断值相同...),这就体现了递归(可根据图理解)
递归的终止条件是出现空节点,结合遍历到头的特殊情况去判断,完整代码如下
代码
python
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def isSymmetric(self, root: Optional[TreeNode]) -> bool:
if root is None:#特判
return True
else:
p=root.left
q=root.right
return self.isMirror(p,q)
def isMirror(self,p: Optional[TreeNode],q: Optional[TreeNode]):
#判断左右子树是否镜像
if p is None or q is None:
return p is q
else:
return p.val==q.val and self.isMirror(p.right,q.left) and self.isMirror(p.left,q.right)