🎬 博主名称 :个人主页
⛺️心简单,世界就简单

目录
序言
到图论这章节了,先讲讲DFS,BFS,然后讲树和图咋存储,还有树和图的DFS以及BFS,
DFS
dfs是一个执着的人(可爱捏),他一直搜索到叶子节点,然后才会回头去看别的路,然后继续一条路走到头
从数据结构来看,我们的dfs用的是栈
从空间来看,我们dfs空间使用是与高度成正比的O( h )
我们dfs搜索是一条路走到头,所以我们dfs不具有最短路的性质
我们来看个最经典的题,
全排列问题
我们从0开始出发,然后往下搜,当搜到n的话就说明我们搜完了输出一下就行(用path记录搜索的路径),当搜完之后,我们肯定要恢复原状,所以把st给回复,path不用是因为,下次直接就覆盖了,不用再path[ i ] = 0;·,,这里的u是层数,我们一层选一个数嘛,到第n层了,那不就是选够n个数了。
cpp
#include <iostream>
using namespace std;
const int N = 10;
int n;
int path[N];
bool st[N];
void dfs(int u){
if(u == n){
for(int i = 0; i < n; i ++) printf("%d" , path[i]);
puts("");
return ;
}
for(int i = 1; i <= n; i ++){
if(!st[i]){
path[u] = i;
st[i] = 1;
dfs(u + 1);
//恢复现场
st[i] = false;
}
}
}
int main(){
cin >> n;
dfs(0);
}我们dfs通常还会有剪枝操作,这里我们拿八皇后问题来讲解
剪枝操作---n皇后问题

序言注意的是,对角线这里
//正对角线 y = x + b; b = x - y; 由于可能为负值,我们加个n 变为x - y +n就行
//反对角线 y = -x + b; b = x + y;
我们这个方式是什么呢,是枚举每一行的位置,看皇后能不能在这
cpp
#include <iostream>
using namespace std;
const int N = 10;
int n;
char g[N][N];
bool col[N], dg[N], udg[N];//列,对角线,反对角线
//正对角线 y = x + b; b = x - y; 由于可能为负值,我们加个n
//反对角线 y = -x + b; b = x + y;
void dfs(int u){
if(u == n){
for(int i = 0; i < n; i++) puts(g[i]);
puts("");
return ;
}
for(int i = 0; i < n; i ++){
if(!col[i] && !dg[u + i] && !udg[n - u + i]){
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n + i - u] = true;
dfs(u + 1);
//恢复现场
g[u][i] = '.';
col[i] = dg[u + i] = udg[n + i - u] = false;
}
}
}
int main(){
cin >> n;
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j ++){
g[i][j] = '.';
}
}
dfs(0);
}BFS
是一个眼观六路,耳听八方的人,他搜索会一层一层搜索,走一次看看哪个好走,再继续搜
从数据结构来看,我们bfs用的是队列
从空间来看,我们bfs空间使用是O( 2^h )
我们BFS搜索时一层一层搜索,每次搜的都是离自己最近的路,所以我们BFS具有一种最短路的性质。
宽搜是有一个固定框架的, 就是建一个队列,然后每次搜到就扔进去,然后取出第一个元素,这个走迷宫也相当于模板了,看看就行,然后我们加了个输出的路径,用prev数组存取每个点的前一步点
cpp
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e2+ 10;
typedef pair<int, int> PII;
int n, m;
int g[N][N];
int d[N][N];//每个点到起点的距离
PII q[N * N], Prev[N][N];
int bfs(){
int hh = 0, tt = 0;
q[0] = {0, 0};
memset(d, -1, sizeof(d));
d[0][0] = 0;
int dx[4] = {-1, 0, 1, 0};
int dy[4] = {0, 1, 0, -1};
while(hh <= tt){
auto t = q[hh++];//取出第一个点,然后
for(int i = 0; i < 4; i++){
int x =t.first +dx[i], y = t.second + dy[i];
if(x >=0 &&x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1){
d[x][y] = d[t.first][t.second] + 1;
Prev[x][y]= t;//记录一下每个点的前一个点
q[ ++tt] = {x, y};//把这个点扔进u低劣里
}
}
}
// int x = n - 1, y = m - 1;
// while(x || y){
// cout << x << ' ' << y <<endl;
// auto t = Prev[x][y];
// x = t.first, y = t.second;
// }
//
return d[n - 1][m - 1];
}
int main(){
cin >> n >>m;
for(int i = 0; i < n; i++){
for(int j = 0; j < m; j++){
cin >> g[i][j];
}
}
cout<<bfs();
}树与图的深度优先遍历
先说树的存储,树是一种特殊的图,他是无环图,那我们就直说图的遍历就行了
树,图的存储
图分为有向图和无向图
无向图就是说如果a和b有之间有边,那就是a能走到b,b也能走向a
有向图就是,说有一条边的话,只能从一个点到另一个点,是有方向的
无向图就是特殊的有向图,我们只讲有向图就行,
有向图可以用邻接表,邻接矩阵来存,我们不常用邻接矩阵,他比较浪费空间,适合稠密的图,稀疏的话就很浪费空间,所以我们一般都用邻接表
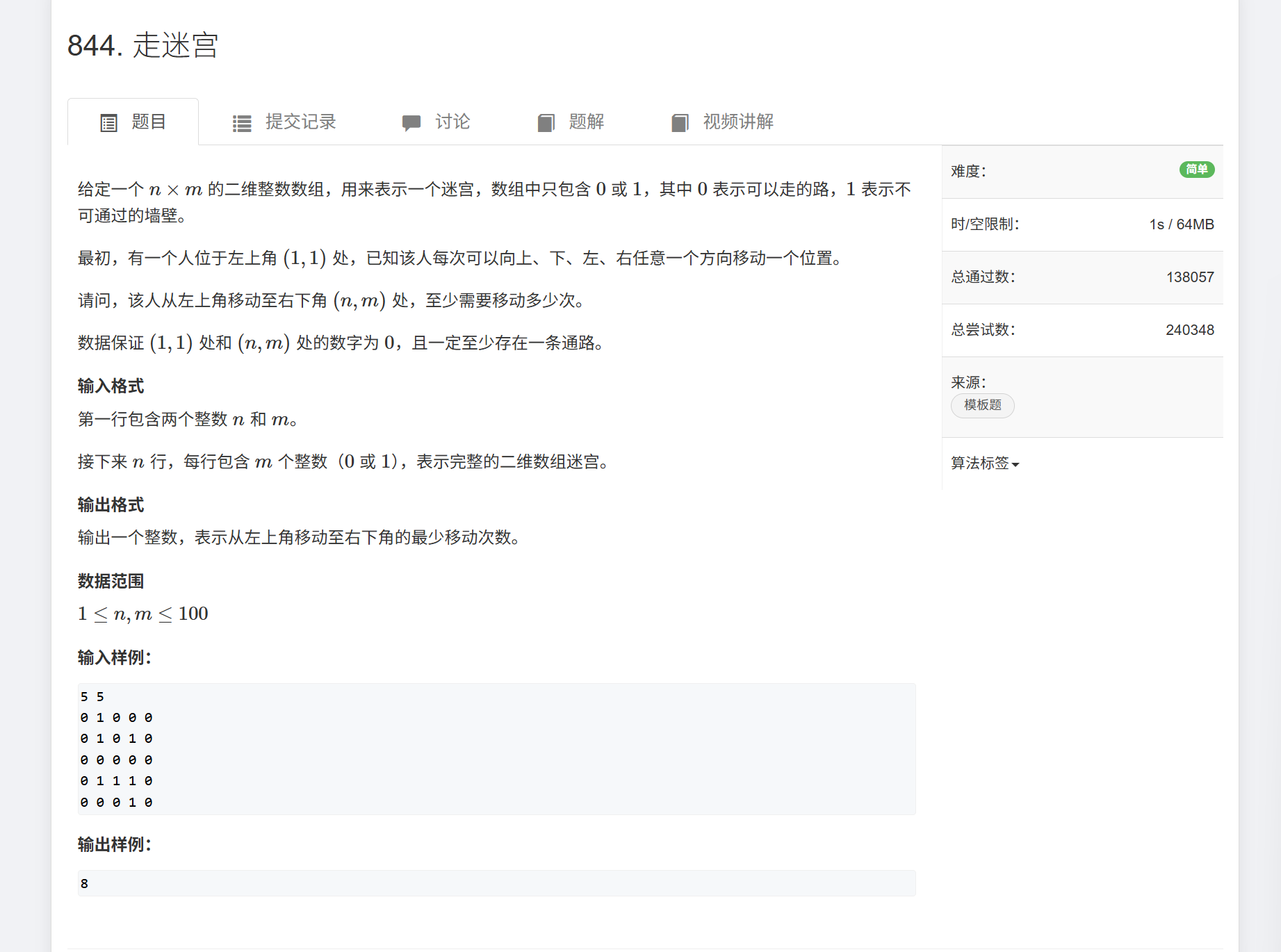
邻接表:就是每个点上都有一个单链表
我们一般都用静态链表,也是常说的链式前向星
cppint h[N], e[M], ne[M], idx; //这个操作的是边,idx是第idx条边,边的编号 void add(int a, int b){ e[idx] = b;//第idx的边的终点是b ne[idx] = h[a]; h[a] = idx ++; }遍历树,图
cppvoid dfs(int u){ st[u] = true;//标记一下已经被搜过了 for (int i = h[u]; i != -1; i = ne[i]){ int j = e[i]; if(!st[j]) dfs(j); } }
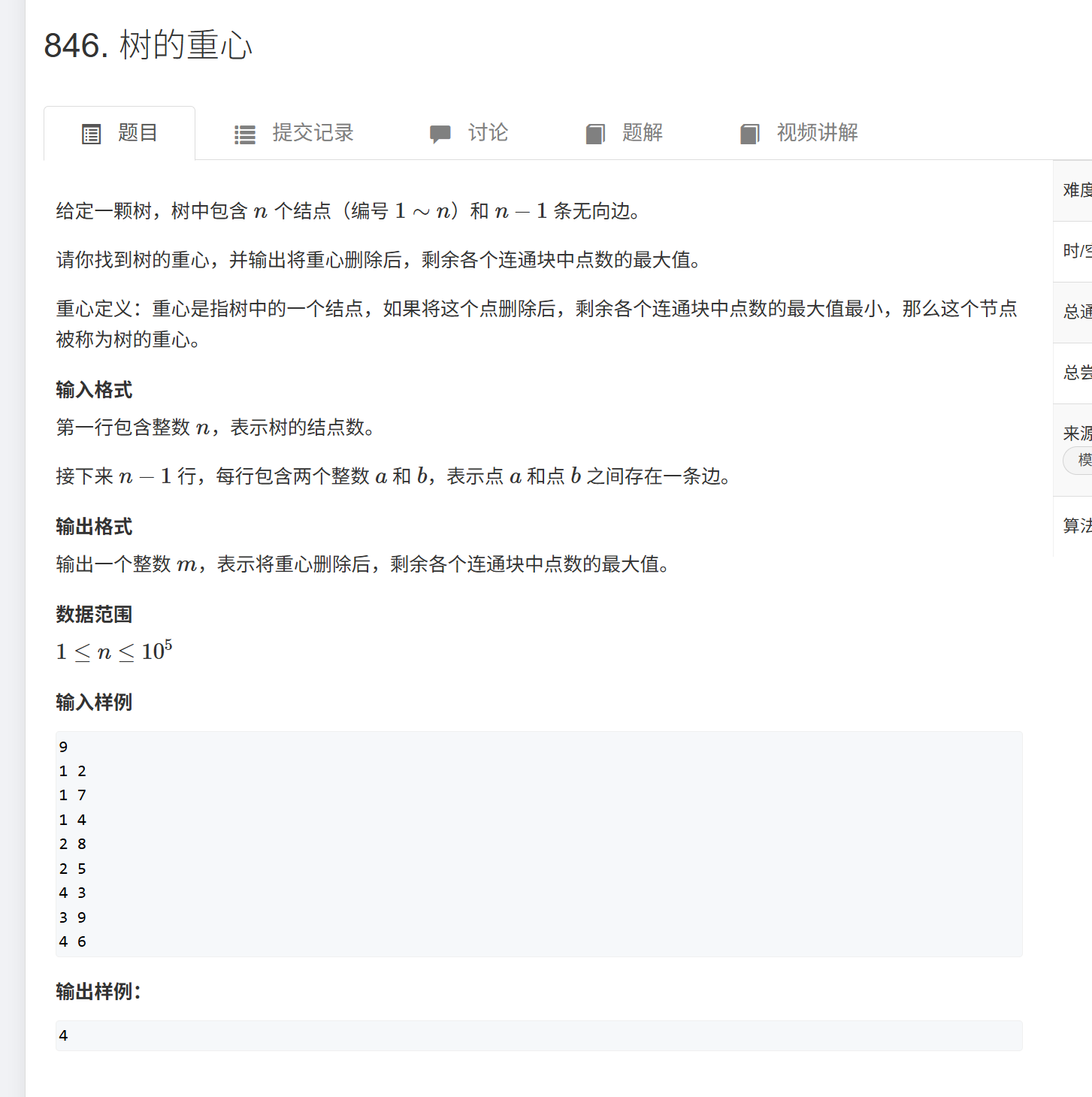
我们去dfs遍历这个图,然后得到以每个节点为根节点,求去掉这个根节点后,他的子树里最大的节点数量为多少,然后我们求出这个最大值,然后用一个全局变量存储,然后和每一个去掉的节点后求得的这个值进行min比较,具体去看代码吧,看代码来思考
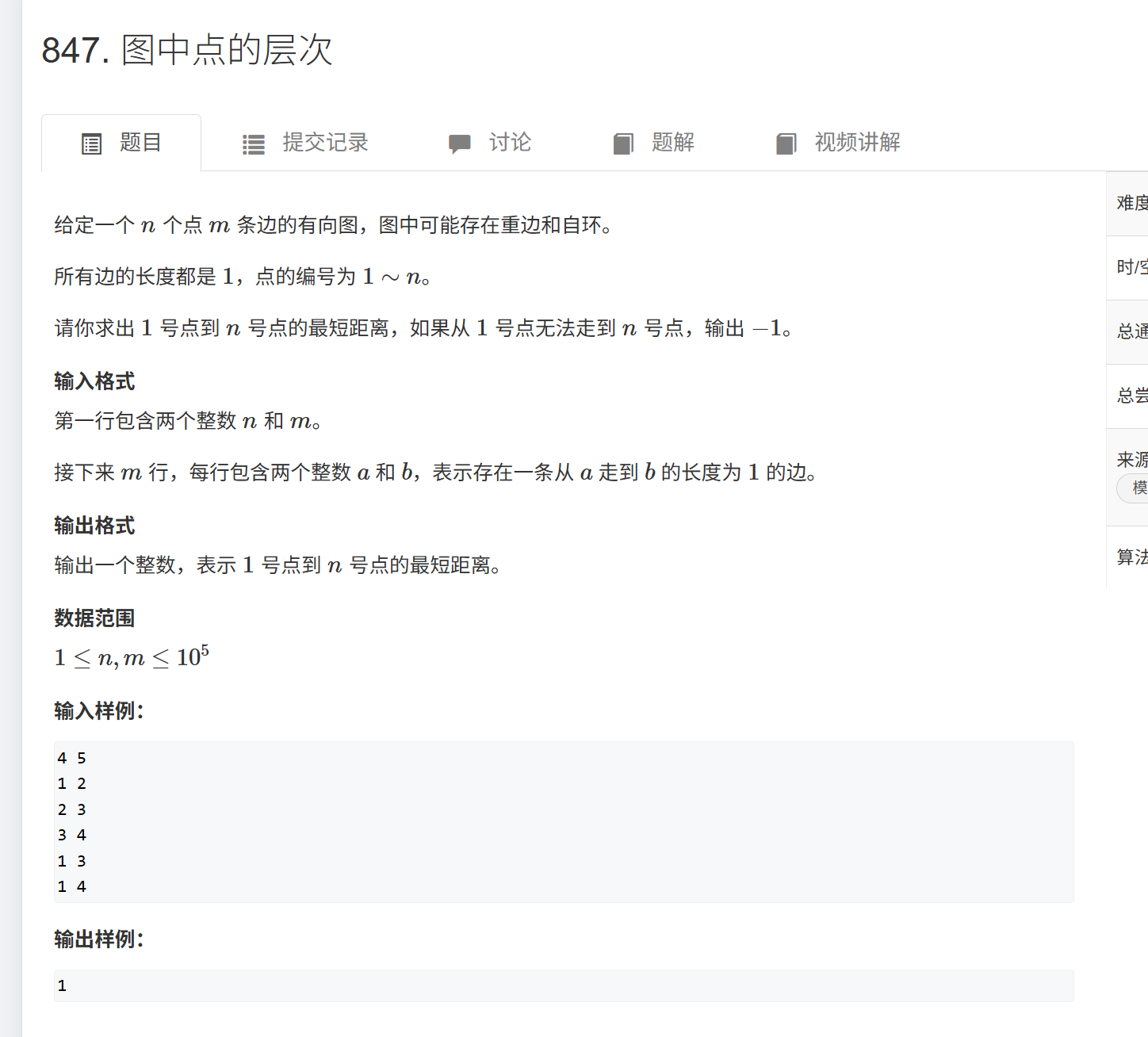
树与图的宽度优先遍历
这个直接找个题看就行了
cpp
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 1e5 +10;
int n, m, q[N], d[N];
//d记录每个节点到节点1的距离
int e[N], h[N], idx, ne[N];
void add(int a, int b){
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int bfs(){
int hh = 0, tt = 0;
q[0] = 1;
memset(d, -1, sizeof d);
d[1] = 0;
while(hh <= tt){
int t = q[hh++];
for(int i = h[t]; i != -1; i = ne[i]){
int j = e[i];
if(d[j] == -1){
d[j] = d[t] + 1;
q[ ++tt] = j;
}
}
}
return d[n];
}
int main(){
cin >> n >> m;
memset(h, -1, sizeof h);
for(int i = 0; i < m; i++){
int a, b;
cin >> a >> b;
add(a, b);
}
cout<< bfs();
}