数据结构基础：B+树如何优化数据库性能

1、B树回顾

前面我们已经学习了B树的相关知识，我们都清楚它的优点：作为一种多路平衡查找树，它通过保持较低的树高，极大地优化了磁盘 I/O。每个节点都包含关键字和数据（或指向数据的指针），查找一个关键字可能在任何一层结束。

主要有以下核心特性：

• 多路平衡搜索树：每个节点可以有多个子节点（2到m个）
• 数据分布 ：所有节点都存储数据（键值对）
• 节点结构：[指针|键|指针|键|...|指针]，键和数据在一起
• 树的高度：相比二叉树大幅降低，减少磁盘I/O
• 自平衡：通过分裂和合并保持平衡

2、B树存在的问题

B树已经很优秀了，为什么还要设计B+树？关键问题在于：

1. 范围查询效率不高： 比如要查找 ID > 100 的所有记录。B 树需要反复地进行中序遍历，这涉及多次从父节点到子节点的往返，I/O 操作频繁且路径复杂。
2. I/O 次数不稳定： 运气好时，数据在根节点或上层节点就能找到；运气不好时，则需要深入到叶子节点。这种查询性能的不稳定性对于数据库系统来说是难以接受的。

B+ 树的设计，正是为了精准地解决这两个问题。

3、B+树的三大核心改进

B+ 树对 B 树进行了三项关键的结构性改造，使其成为数据库索引的理想选择。

3.1、升级一：非叶子节点"纯粹化"

在 B+ 树中，所有的非叶子节点（内部节点）都变成了**纯粹的索引。**它们不再存储任何数据，只存储关键字和指向下一层节点的指针。

结果： 因为去掉了数据，一个磁盘页（节点）现在可以容纳更多的关键字。这使得树的扇出变得更大，树的高度被进一步压缩，I/O 次数变得更少。

3.2、升级二：数据"下沉"到叶子节点

B+ 树中，所有的数据记录都必须存储在叶子节点。非叶子节点中的关键字，仅仅是叶子节点中关键字的一个"副本"或"冗余索引"。

结果： 任何一次查询，无论成功与否，都必须从根走到某一个叶子节点才能结束。这保证了查询性能的绝对稳定，每一次查询的 I/O 次数都是相同的。

3.3、升级三：叶子节点"串联化"

B+ 树的所有叶子节点通过指针相互连接，形成一个有序的双向链表。

结果： 这项改进对于范围查询是革命性的。一旦定位到范围的起始点，只需沿着叶子节点的链表顺序向后扫描即可，无需再回溯到上层节点。这使得范围查询的效率极高，几乎等同于一次定位 + 一次顺序读。

B树与B+树结构对比（阶m=4）

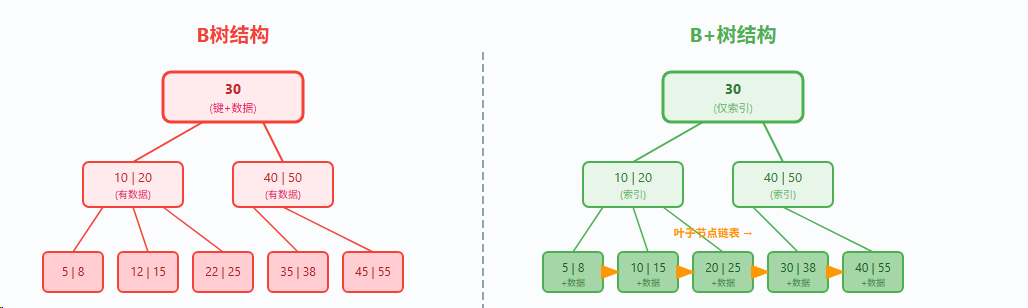
B树每个节点都存数据，B+树只有叶子存数据，内部节点纯索引

4、B+树的性能提升

B+树这三大升级共同作用，使得 B+ 树在与磁盘交互时表现得极为高效。

4.1、磁盘IO效率提升

数据库性能优化的核心就是减少磁盘 I/O。B+ 树的"矮胖"结构是关键。由于非叶子节点不存数据，一个 4KB 的磁盘页可以放下成百上千个关键字，这让树的扇出极大，高度极低。存储上亿条数据，树高可能仅为 3-4 层。这意味着大部分查询只需 3-4 次磁盘 I/O，再配合内存缓存，实际 I/O 可能只有 1-2 次，性能得到巨大提升。

我们看一个示例：阶m=200的树，100万条数据

假设条件：

• 键：8字节（BIGINT）
• 指针：8字节
• 数据记录：200字节
• 磁盘页：4KB（4096字节）

B树：

• 每个节点：(200键×8字节) + (200数据×200字节) + (201指针×8字节) = 41,608字节
• 需要11个磁盘页才能存一个节点！
• 实际一个页只能存：4096÷(8+200+8) ≈ 19个键值对
• 100万数据，树高约：log₁₉(1000000) ≈ 4.7层 → 5层

B+树：

• 内部节点：(200键×8字节) + (201指针×8字节) = 3,208字节 → 刚好一页！
• 100万数据，树高约：log₂₀₀(1000000) ≈ 2.6层 → 3层
• 磁盘I/O：3次 vs 5次，性能提升40%！

4.2、范围查询提升

数据库的80%以上查询都是范围查询或顺序扫描，而不是单点查询， 对于 BETWEEN, >, < 等范围查询，B+ 树的叶子链表结构提供了无与比拟的优势。B 树需要复杂的树遍历来完成这个任务，而 B+ 树只需简单地在链表上"滑行"，这是一个从"随机读"到"顺序读"的质变，效率天差地别

B树的范围查询：低效的"往返跑"

B树要进行范围查询，必须执行类似中序遍历的操作。这需要在树的层级之间反复地上下来回移动，每次移动都可能触发新的磁盘I/O。

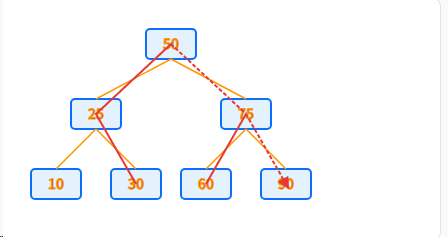
查询 >25 的路径，需要在父子节点间反复跳转。

B+树的范围查询：高效的"顺序读"

B+树只需先定位到范围的起始点（一次B+树查找），然后利用叶子节点的链表，顺序地向后读取即可。这是一个从"随机读"到"顺序读"的质变。

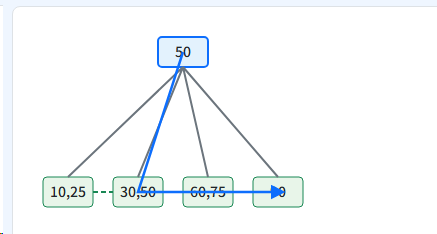
查询 >25，定位到30后，沿链表顺序扫描即可。

5、B+树的核心操作

5.1、查找操作

B+树的查找与B树有何不同？

关键区别：

• B树：找到键值即返回，可能在任何层
• B+树 ：必须到达叶子节点，即使内部节点有相同的键

原因：内部节点的键只是索引，真正的数据在叶子节点！

查找算法流程

1. 从根节点开始
2. 在当前节点找到第一个大于key的键K[i]，走对应指针P[i-1]
3. 如果是内部节点，继续步骤2；如果是叶子节点，查找key并返回

示例

查找 key=35，返回对应的数据

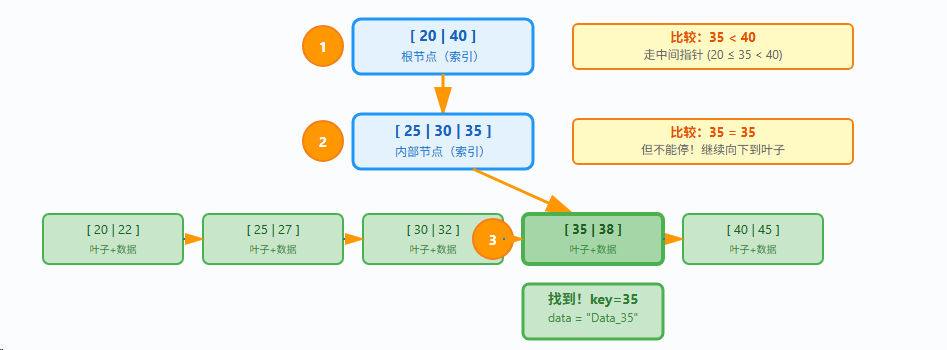
1. **Step 1:**根节点：35 < 40，走中间指针
2. Step 2: 到达内部节点：35 = 35，但继续向下（索引不是数据！）。
3. Step 3: 到达 叶子节点：找到 key=35，返回 data="Data_35"
4. 磁盘I/O：3次

关键点：

• 即使在内部节点找到相同的键，也必须继续向下__：内部节点的键只是索引路标，真正的数据在叶子节点。
• 每次比较：找到第一个大于目标key的键，走其左边的指针。
• 磁盘I/O：每访问一个节点=1次I/O，树高=3，所以3次I/O。

5.2、插入操作

插入操作总是发生在叶子节点。核心是处理叶子节点满员后的分裂。分裂可能向上传播，甚至导致树长高！

插入流程

1. 查找：找到key应该插入的叶子节点L
2. 插入：将(key, data)插入L，保持有序
3. 检查溢出 ：
   • 如果键值数 ≤ m-1：完成
   • 如果键值数 > m-1：分裂节点
4. 分裂叶子节点 ：
   • 创建新节点L'，将后⌈m/2⌉个键值移到L'
   • 将L'的第一个键复制到父节点
   • 更新叶子链表
5. 向上传播：如果父节点溢出，继续分裂

关键！ 叶子节点分裂：中间键复制到父节点（叶子保留完整数据）

内部节点分裂：中间键上移到父节点（内部节点删除，注意不是复制过去）

为何叶子分裂是"复制" ，而内部节点是"移动"？

这是 B+ 树与 B 树在插入操作上最核心的区别，其根本原因是为了维持"所有数据记录都必须存在于叶子节点，且叶子节点通过链表相连"这一核心原则。

1. 叶子节点分裂：必须"复制"

当一个叶子节点溢出并分裂时，它是在分割数据记录。假设原始叶子节点内容为 [20(D), 25(D), 27(D), 28(D)]，中间关键字是 27。分裂后，我们将它分为 [20(D), 25(D)] 和 [27(D), 28(D)]。

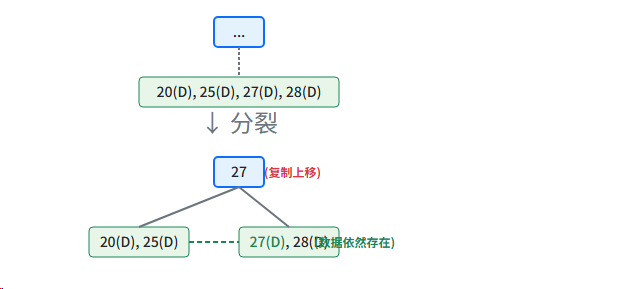
关键字 27(D) 本身是一条完整的数据记录（在 B+ 树中，这意味着它包含了实际存储的数据）。如果我们将它"移动"到父节点，叶子层就会丢失 27(D) 这条实际的数据记录，这违反了 B+ 树"所有数据都必须在叶子节点"的根本设计。因此，我们必须：

• 在新的右侧叶子节点 [27(D), 28(D)] 中保留27(D) 这条数据记录。
• 同时，将 27 这个关键字复制一份到父节点，作为导航到新右侧节点的"路标"或索引。

这样，无论通过树的内部节点索引路径查找 27，还是通过叶子链表进行范围查询，都能找到 27(D) 这条数据。

2. 内部节点分裂：可以"移动"

当一个内部（索引）节点溢出并分裂时，它是在分割索引项。这些索引项本身不包含实际数据记录，它们仅仅是帮助查找的"路标"。假设原始内部节点内容为 [10, 20, 30, 40]，中间关键字是 20。

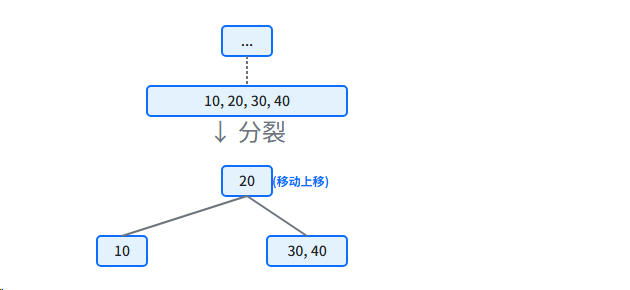
内部节点中的关键字（如 20）纯粹是索引，它只表示一个范围的分界点。当内部节点分裂时，这个中间关键字 20 的作用是作为新分裂出的两个子节点 [10] 和 [30, 40] 的"分界线"。它在子节点层已经完成了作为分界点的使命，不再需要保留。把它直接移动到父节点，既能继续作为父节点新的索引，又避免了冗余，使索引层尽可能紧凑。因为它不代表任何真实数据，所以"移动"它完全没有问题。

示例

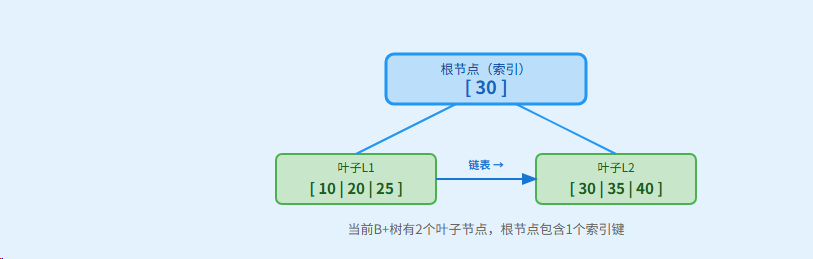
插入 key=28 到B+树（阶m=4，最多3个键）

步骤1: 初始状态

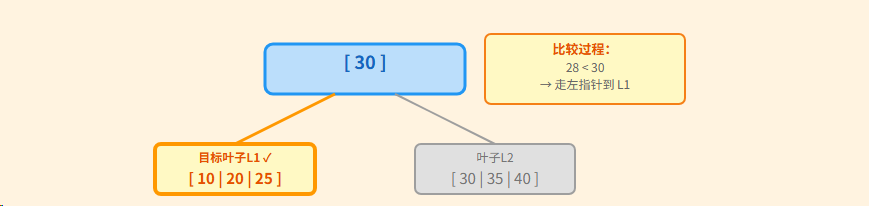
步骤2: 找到插入位置

步骤3: 插入28，节点溢出

步骤4: 分裂叶子节点

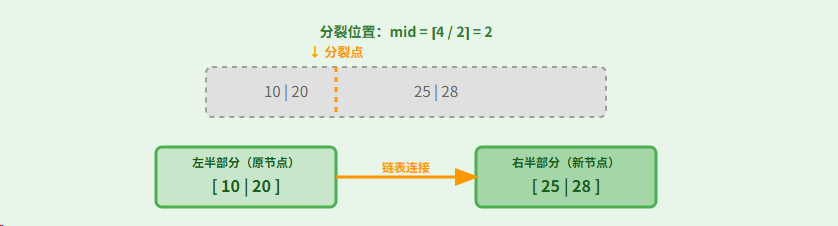
步骤5: 复制第一个键到父节点

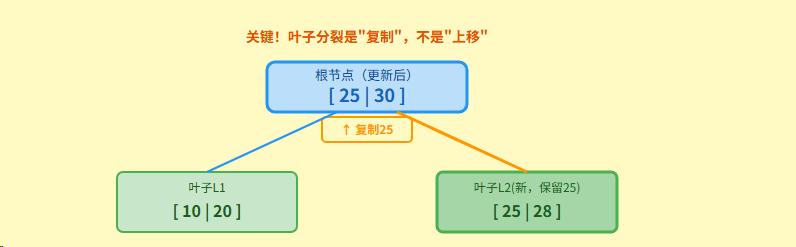
步骤 6： 插入完成！最终结构

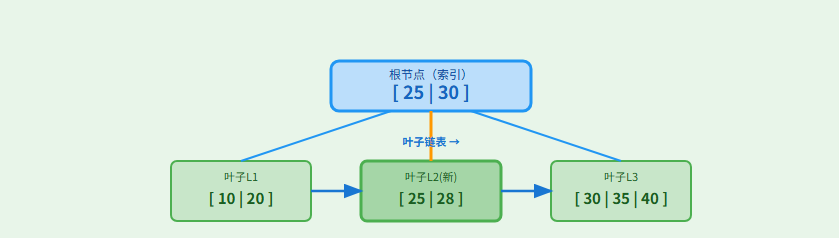
叶子分裂的关键点：

• 复制vs上移 ：叶子节点分裂时，中间键 复制 到父节点，叶子保留；内部节点分裂时，中间键 上移到父节点，内部节点删除。
• ***为什么？*因为叶子存储所有数据，必须保留完整；内部节点只是索引，可以删除。
• 链表更新：新节点插入到链表中，保持顺序访问能力。
• 分裂传播：如果父节点也溢出，继续向上分裂，可能导致树长高。

5.3、删除操作

删除操作的核心是处理节点关键字过少后的下溢 ，通过与兄弟节点合并 或向其借用来解决。

删除流程

1. 查找并删除：找到key所在的叶子节点，删除(key, data)
2. 检查下溢 ：
   • 如果键值数 ≥ ⌈m/2⌉-1：完成
   • 如果键值数 < ⌈m/2⌉-1：需要调整
3. 尝试从兄弟节点借 ：
   • 如果左/右兄弟有富余，借一个键值
   • 更新父节点的索引键
4. 合并节点 （如果借不到）：
   • 与左或右兄弟合并
   • 删除父节点中的对应键
5. 向上传播：如果父节点下溢，继续处理

示例

阶m=5，最少2个键，删除 key=10 后节点下溢，需要从兄弟借键或合并

步骤1: 初始状态

步骤2: 删除key=10

步骤3: 从右兄弟借键

删除操作的策略：

• 优先借键：如果兄弟节点有富余（键数>最小值），借一个键来平衡。
• 无法借则合并：如果左右兄弟都没有富余，将当前节点与兄弟合并。
• 向上传播：合并后父节点会少一个键，如果父节点下溢，继续向上处理。
• 更新索引：借键或合并后，需要更新父节点的索引键。

删除操作的常见误区

一个常见的疑问是：当删除一个同时存在于叶子节点和内部节点（作为索引）的键时，应该先删除哪个？例如，删除下图中的键 20：

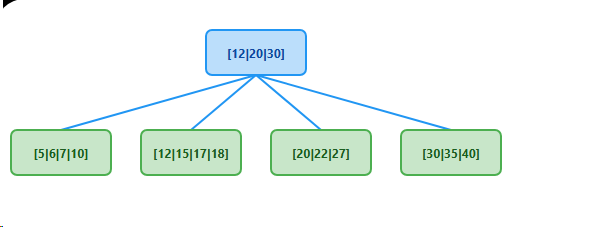
答案：永远先删除叶子节点的数据记录 20(D)。

• 原因： B+ 树的核心是数据存储在叶子层。删除操作的根本目的是移除数据记录。内部节点中的 20 只是一个索引，它的存在是为了正确导航到包含 20(D) 的叶子节点。
• 操作流程：
  1. 找到叶子节点 [20(D), 22(D), 27(D)] 并删除 20(D)，节点变为 [22(D), 27(D)]。
  2. 检查该叶子节点是否下溢。如果未下溢，则操作结束。父节点的索引 20 保持不变，因为它仍然可以正确地指导查找（小于20走左子树，大于等于20走右子树，现在右子树的最小值是22，依然符合规则）。
  3. 如果叶子节点下溢，则执行合并或借用。只有在这个时候，为了调整树结构，父节点的索引 20 才可能会被更新或删除。
• 关键点： 内部节点的索引关键字是被动调整的，它的变化取决于叶子节点删除数据后的状态，而不是被主动删除。

5.4、范围查询

这是B+树相比B树的最大优势！

范围查询流程（查询key1到key2之间的所有数据）

1. 查找key1所在的叶子节点（O(log n)）
2. 从该节点开始，沿着叶子链表顺序遍历
3. 收集所有key1 ≤ key ≤ key2的数据
4. 当key > key2时停止

示例

查询范围 [22, 38] 之间的所有数据（SQL: WHERE key BETWEEN 22 AND 38）

从根节点查找 key=22，找到叶子节点 [20, 22, 25]

扫描链表：

① 节点 [20, 22, 25]：收集 22, 25

② 沿链表到下一节点 [30, 32, 35]：收集 30, 32, 35 （+1次I/O）

③ 下一节点 [38, 39]：收集 38，39 > 38，停止 （+1次I/O）

查询结果：[22, 25, 30, 32, 35, 38]

总I/O：5次（3次查找 + 2次顺序读）

范围查询的性能优势：

• 顺序I/O vs 随机I/O ：沿着叶子链表扫描是 顺序磁盘访问，速度是随机访问的10-100倍！
• 最小I/O次数：只需访问包含结果的叶子节点，不访问无关节点。
• SQL优化：数据库的 WHERE、ORDER BY、GROUP BY 都依赖范围查询，B+树完美支持。
• 实际案例：查询年龄在20-30岁的用户，B+树可能只需5次I/O，B树可能需要50+次！

6、时间复杂度分析

B+ 树的性能优势也可以通过其时间复杂度来体现，尤其是在分析磁盘 I/O 次数时。假设树的阶为 m，总数据条数为 N，树的高度为 h (h ≈ logₘ(N))。

操作	时间复杂度 (I/O)	备注 (h = logₘ(N) )
查找	O(h)或 O(logₘ(N))	从根节点到叶子节点的一次遍历，即树的高度。
插入	O(h)或 O(logₘ(N))	首先需要 O(h)查找到叶子节点。最坏情况下，分裂操作会一路传播到根节点，需要 O(h)次写操作。
删除	O(h)或 O(logₘ(N))	与插入类似。O(h)查找，最坏情况下，合并或借用操作会一路传播到根节点。
范围查找	O(h + L)	O(h)查找到起始叶子节点，然后通过链表顺序扫描 L个叶子节点（磁盘页）。L是包含结果集的叶子节点数。

7、B树和B+树的对比

对比维度	B树	B+树
数据位置	所有节点都存储数据	只有叶子节点存储数据
空间利用	单页存储键值少→树更高	单页存储键值多（10-20倍）→树更矮
查询路径	找到即返回，路径长度不一	必须到叶子节点，路径长度相同
范围查询	需要中序遍历，多次回溯	沿着叶子链表遍历，非常高效
顺序访问	需要遍历整棵树	直接遍历叶子链表
查询性能	不稳定（1到h次I/O）	稳定（始终h次I/O）
磁盘I/O	较多（树高）	较少（树矮）
适用场景	文件系统	数据库索引（主流）

8、Python完整实现

#!/usr/bin/env python3
# -*- coding: utf-8 -*-


class Node:
    """B+树节点类"""
    def __init__(self, is_leaf=False):
        self.keys = []          # 键列表
        self.children = []      # 子节点指针列表（内部节点使用）
        self.data = []          # 数据列表（叶子节点使用）
        self.is_leaf = is_leaf  # 是否为叶子节点
        self.next = None        # 指向下一个叶子节点（构成链表）
        self.parent = None      # 父节点指针


class BPlusTree:
    """B+树实现"""
    def __init__(self, order=4):
        """
        初始化B+树
        
        参数:
            order: 树的阶，每个节点最多order-1个键，最多order个子节点
        """
        self.order = order
        self.root = Node(is_leaf=True)
    
    def search(self, key):
        """
        查找键值key对应的数据
        
        参数:
            key: 要查找的键
        
        返回:
            对应的数据，如果不存在返回None
        """
        node = self._find_leaf(key)
        
        if key in node.keys:
            index = node.keys.index(key)
            return node.data[index]
        return None
    
    def _find_leaf(self, key):
        """
        找到key应该在的叶子节点
        
        参数:
            key: 要查找的键
        
        返回:
            应该包含key的叶子节点
        """
        node = self.root
        
        # 从根节点向下查找
        while not node.is_leaf:
            # 找到第一个大于key的键的位置
            i = 0
            while i < len(node.keys) and key >= node.keys[i]:
                i += 1
            node = node.children[i]
        
        return node
    
    def insert(self, key, data):
        """
        插入键值对(key, data)
        
        参数:
            key: 键
            data: 对应的数据
        """
        leaf = self._find_leaf(key)
        
        # 如果键已存在，更新数据
        if key in leaf.keys:
            index = leaf.keys.index(key)
            leaf.data[index] = data
            return
        
        # 插入到叶子节点（保持有序）
        i = 0
        while i < len(leaf.keys) and key > leaf.keys[i]:
            i += 1
        leaf.keys.insert(i, key)
        leaf.data.insert(i, data)
        
        # 检查是否需要分裂
        if len(leaf.keys) >= self.order:
            self._split_leaf(leaf)
    
    def _split_leaf(self, leaf):
        """
        分裂叶子节点
        
        参数:
            leaf: 要分裂的叶子节点
        """
        # 创建新节点
        new_leaf = Node(is_leaf=True)
        mid = len(leaf.keys) // 2
        
        # 将后半部分键值移到新节点
        new_leaf.keys = leaf.keys[mid:]
        new_leaf.data = leaf.data[mid:]
        leaf.keys = leaf.keys[:mid]
        leaf.data = leaf.data[:mid]
        
        # 更新叶子节点链表
        new_leaf.next = leaf.next
        leaf.next = new_leaf
        
        # 复制第一个键到父节点（注意是复制，不是移动）
        new_key = new_leaf.keys[0]
        self._insert_in_parent(leaf, new_key, new_leaf)
    
    def _insert_in_parent(self, left, key, right):
        """
        在父节点中插入键和指向新节点的指针
        
        参数:
            left: 左子节点
            key: 要插入父节点的键
            right: 右子节点
        """
        if left == self.root:
            # 根节点分裂，创建新根
            new_root = Node(is_leaf=False)
            new_root.keys = [key]
            new_root.children = [left, right]
            self.root = new_root
            left.parent = new_root
            right.parent = new_root
            return
        
        parent = left.parent
        # 找到left在父节点中的位置
        index = parent.children.index(left)
        
        # 插入键和指针
        parent.keys.insert(index, key)
        parent.children.insert(index + 1, right)
        right.parent = parent
        
        # 检查父节点是否需要分裂
        if len(parent.keys) >= self.order:
            self._split_internal(parent)
    
    def _split_internal(self, node):
        """
        分裂内部节点
        
        参数:
            node: 要分裂的内部节点
        """
        new_node = Node(is_leaf=False)
        mid = len(node.keys) // 2
        
        # 中间键上移到父节点，其余键分裂
        split_key = node.keys[mid]
        new_node.keys = node.keys[mid + 1:]
        new_node.children = node.children[mid + 1:]
        node.keys = node.keys[:mid]
        node.children = node.children[:mid + 1]
        
        # 更新子节点的父指针
        for child in new_node.children:
            child.parent = new_node
        
        # 将split_key插入父节点
        self._insert_in_parent(node, split_key, new_node)
    
    def delete(self, key):
        """
        删除键值key
        
        参数:
            key: 要删除的键
        
        注意:
            这是简化版删除，不处理节点下溢的所有情况
        """
        leaf = self._find_leaf(key)
        
        if key not in leaf.keys:
            return  # 键不存在
        
        # 删除键值对
        index = leaf.keys.index(key)
        leaf.keys.pop(index)
        leaf.data.pop(index)
    
    def range_query(self, key1, key2):
        """
        范围查询：返回[key1, key2]之间的所有键值对
        
        参数:
            key1: 范围起始键
            key2: 范围结束键
        
        返回:
            包含(key, data)元组的列表
        """
        result = []
        node = self._find_leaf(key1)
        
        # 沿着叶子节点链表遍历
        while node:
            for i, key in enumerate(node.keys):
                if key1 <= key <= key2:
                    result.append((key, node.data[i]))
                elif key > key2:
                    return result
            node = node.next
        
        return result
    
    def print_tree(self):
        """以层次遍历方式打印树结构"""
        if not self.root:
            print("树为空")
            return
        
        queue = [(self.root, 0)]  # (节点, 层级)
        current_level = 0
        
        while queue:
            node, level = queue.pop(0)
            
            if level > current_level:
                print()
                current_level = level
            
            # 打印节点
            node_type = "叶子" if node.is_leaf else "索引"
            print(f"[{node_type}:{node.keys}]", end=" ")
            
            # 添加子节点到队列
            if not node.is_leaf:
                for child in node.children:
                    queue.append((child, level + 1))
        
        print("\n")
    
    def get_height(self):
        """获取树的高度"""
        height = 0
        node = self.root
        while node and not node.is_leaf:
            height += 1
            node = node.children[0]
        return height + 1
    
    def count_keys(self):
        """统计树中键的总数"""
        count = 0
        queue = [self.root]
        
        while queue:
            node = queue.pop(0)
            if node.is_leaf:
                count += len(node.keys)
            else:
                queue.extend(node.children)
        
        return count


if __name__ == "__main__":
    print("=" * 60)
    print("B+树完整实现测试")
    print("=" * 60)
    
    # 创建B+树，阶为4
    tree = BPlusTree(order=4)
    
    # 测试1：插入数据
    print("\n【测试1：插入数据】")
    test_data = [5, 10, 15, 20, 25, 30, 35, 40, 45, 50]
    print(f"插入数据：{test_data}")
    
    for key in test_data:
        tree.insert(key, f"Data_{key}")
        print(f"  插入 {key:2d} -> Data_{key}")
    
    print("\n树结构：")
    tree.print_tree()
    
    # 统计信息
    print(f"树高度：{tree.get_height()}")
    print(f"键总数：{tree.count_keys()}")
    
    # 测试2：查找数据
    print("\n【测试2：查找数据】")
    search_keys = [25, 99, 5, 50]
    for key in search_keys:
        result = tree.search(key)
        if result:
            print(f"  查找 {key:2d}: 找到 -> {result}")
        else:
            print(f"  查找 {key:2d}: 未找到")
    
    # 测试3：范围查询
    print("\n【测试3：范围查询】")
    ranges = [(10, 30), (5, 15), (35, 60)]
    
    for start, end in ranges:
        results = tree.range_query(start, end)
        print(f"  范围[{start}, {end}]:")
        for key, data in results:
            print(f"    {key} -> {data}")
    
    # 测试4：删除数据
    print("\n【测试4：删除数据】")
    delete_keys = [25, 40]
    for key in delete_keys:
        tree.delete(key)
        print(f"  删除 {key}")
    
    print("\n删除后的树结构：")
    tree.print_tree()
    print(f"键总数：{tree.count_keys()}")
    
    # 测试5：大量数据测试
    print("\n【测试5：大量数据测试】")
    large_tree = BPlusTree(order=5)
    
    import random
    large_data = list(range(1, 101))
    random.shuffle(large_data)
    
    print(f"插入100个随机数据...")
    for key in large_data:
        large_tree.insert(key, key * 100)
    
    print(f"树高度：{large_tree.get_height()}")
    print(f"键总数：{large_tree.count_keys()}")
    
    # 验证范围查询
    range_result = large_tree.range_query(40, 60)
    print(f"\n范围查询[40, 60]：找到 {len(range_result)} 条记录")
    print(f"前5条：{range_result[:5]}")


# ============================================================
# B+树完整实现测试
# ============================================================

# 【测试1：插入数据】
# 插入数据：[5, 10, 15, 20, 25, 30, 35, 40, 45, 50]
#   插入  5 -> Data_5
#   插入 10 -> Data_10
#   插入 15 -> Data_15
#   插入 20 -> Data_20
#   插入 25 -> Data_25
#   插入 30 -> Data_30
#   插入 35 -> Data_35
#   插入 40 -> Data_40
#   插入 45 -> Data_45
#   插入 50 -> Data_50

# 树结构：
# [索引:[35]] 
# [索引:[15, 25]] [索引:[45]] 
# [叶子:[5, 10]] [叶子:[15, 20]] [叶子:[25, 30]] [叶子:[35, 40]] [叶子:[45, 50]] 

# 树高度：3
# 键总数：10

# 【测试2：查找数据】
#   查找 25: 找到 -> Data_25
#   查找 99: 未找到
#   查找  5: 找到 -> Data_5
#   查找 50: 找到 -> Data_50

# 【测试3：范围查询】
#   范围[10, 30]:
#     10 -> Data_10
#     15 -> Data_15
#     20 -> Data_20
#     25 -> Data_25
#     30 -> Data_30
#   范围[5, 15]:
#     5 -> Data_5
#     10 -> Data_10
#     15 -> Data_15
#   范围[35, 60]:
#     35 -> Data_35
#     40 -> Data_40
#     45 -> Data_45
#     50 -> Data_50

# 【测试4：删除数据】
#   删除 25
#   删除 40

# 删除后的树结构：
# [索引:[35]] 
# [索引:[15, 25]] [索引:[45]] 
# [叶子:[5, 10]] [叶子:[15, 20]] [叶子:[30]] [叶子:[35]] [叶子:[45, 50]] 

# 键总数：8

# 【测试5：大量数据测试】
# 插入100个随机数据...
# 树高度：4
# 键总数：100

# 范围查询[40, 60]：找到 21 条记录
# 前5条：[(40, 4000), (41, 4100), (42, 4200), (43, 4300), (44, 4400)]

9、可视化演示

https://code.juejin.cn/pen/7564257557009203250?embed=true

10、总结

从 B 树到 B+ 树的演进，并不是一次彻底的颠覆，而是一次"针对性"的完美优化。

B+ 树放弃了 B 树在非叶子节点存储数据的灵活性，以此换来了：

1. 因内部节点"纯粹化"而带来的更矮的树高 和更少的 I/O。
2. 因数据"全部下沉"而带来的绝对稳定的查询性能。
3. 因叶子节点"串联化"而带来的无与伦比的范围查询效率。

这三大特性，完美契合了数据库和文件系统"I/O 密集型"和"范围查询密集型"的应用场景，使其成为了现代数据存储领域当之无愧的基石。