第八章:PID 控制器的参数整定
前言
欢迎进入第八章:PID 控制器的参数整定。
如果说第七章的极点配置和 LQR 是"手术刀",那么 PID 控制器就是工业界的"大米白面"。据统计,全球 95% 以上的工业控制回路(从恒温热水器到化工生产线)都在使用 PID 算法。
PID 的魅力在于其结构简单、不完全依赖受控对象的精确数学模型 。但 PID 的难点在于"整定"------即如何确定 K p , K i , K d K_p, K_i, K_d Kp,Ki,Kd 这三个参数。本章我们将学习 MATLAB 提供的各种 PID 建模工具、自动整定函数,以及在 Simulink 中如何高效地调试 PID 回路。
一、 核心原理与知识点汇总
- PID 结构 :
- P(比例):反应当前的误差,消除误差最快。
- I(积分) :反应累积的误差,用于消除静差。
- D(微分) :反应误差的变化趋势,具有超前预判作用,能减少超调。
- PID 的表现形式 :
- 并联型(Parallel) : C ( s ) = K p + K i s + K d s C(s) = K_p + \frac{K_i}{s} + K_d s C(s)=Kp+sKi+Kds(MATLAB 默认)。
- 标准型(Standard) : C ( s ) = K p ( 1 + 1 T i s + T d s ) C(s) = K_p (1 + \frac{1}{T_i s} + T_d s) C(s)=Kp(1+Tis1+Tds)。
- 整定方法 :
- 传统法:齐格勒-尼科尔斯(Ziegler-Nichols)经验公式。
- 自动法:基于频率响应的自动整定技术(MATLAB 强项)。
- 最优法:利用 ITAE、ISE 等误差性能指标进行最优化搜索。
二、 必会 MATLAB 函数清单
1. pid() ------ 创建 PID 控制器对象
-
功能:建立一个 PID 模型,用于后续的闭环分析。
-
输入 : K p , K i , K d K_p, K_i, K_d Kp,Ki,Kd。
-
返回值:PID 模型对象。
-
代码示例 :
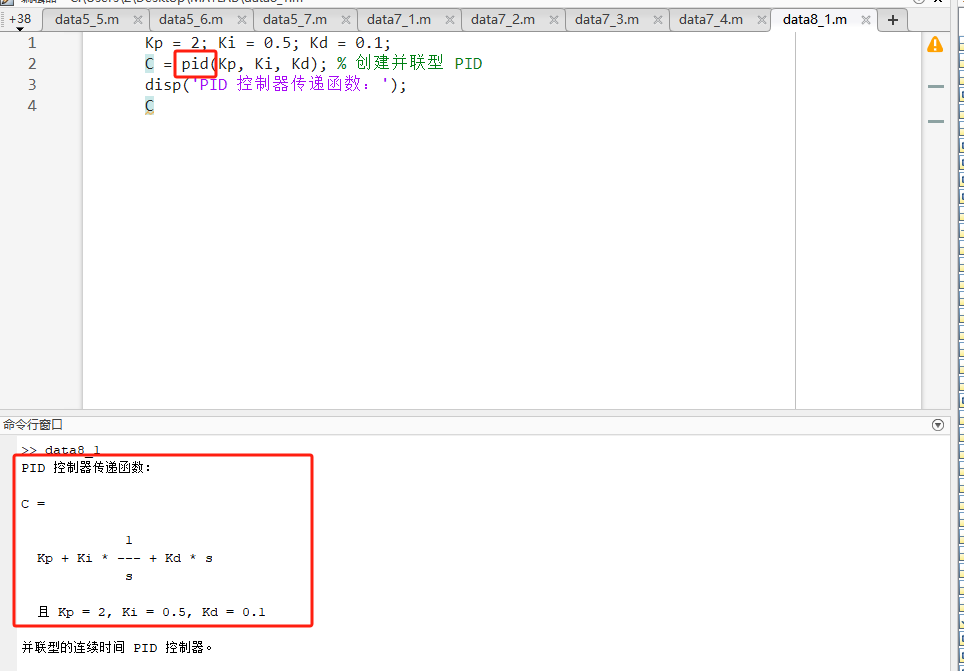
matlabKp = 2; Ki = 0.5; Kd = 0.1; C = pid(Kp, Ki, Kd); % 创建并联型 PID disp('PID 控制器传递函数:'); C -
源码讲解 :直接通过系数定义。如果是标准型,可以使用
pidstd(Kp, Ti, Td)。 -
预期输出 :
2. pidtune() ------ PID 参数自动整定(核心函数)
-
功能 :针对指定的受控对象
G,自动计算出满足系统稳定性和鲁棒性的 PID 参数。 -
输入 :受控对象
G,控制器类型(如 'PI' 或 'PID')。 -
返回值 :整定好的控制器
C,以及整定信息info。 -
代码示例 :
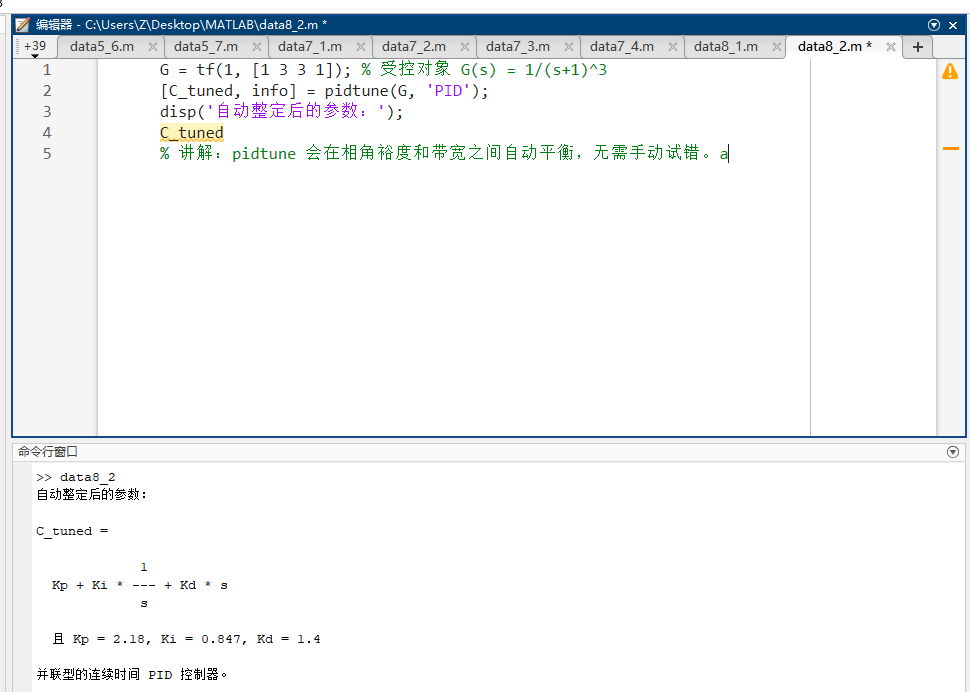
matlabG = tf(1, [1 3 3 1]); % 受控对象 G(s) = 1/(s+1)^3 [C_tuned, info] = pidtune(G, 'PID'); disp('自动整定后的参数:'); C_tuned % 讲解:pidtune 会在相角裕度和带宽之间自动平衡,无需手动试错。
3. pidtool() ------ 交互式 PID 调试窗口
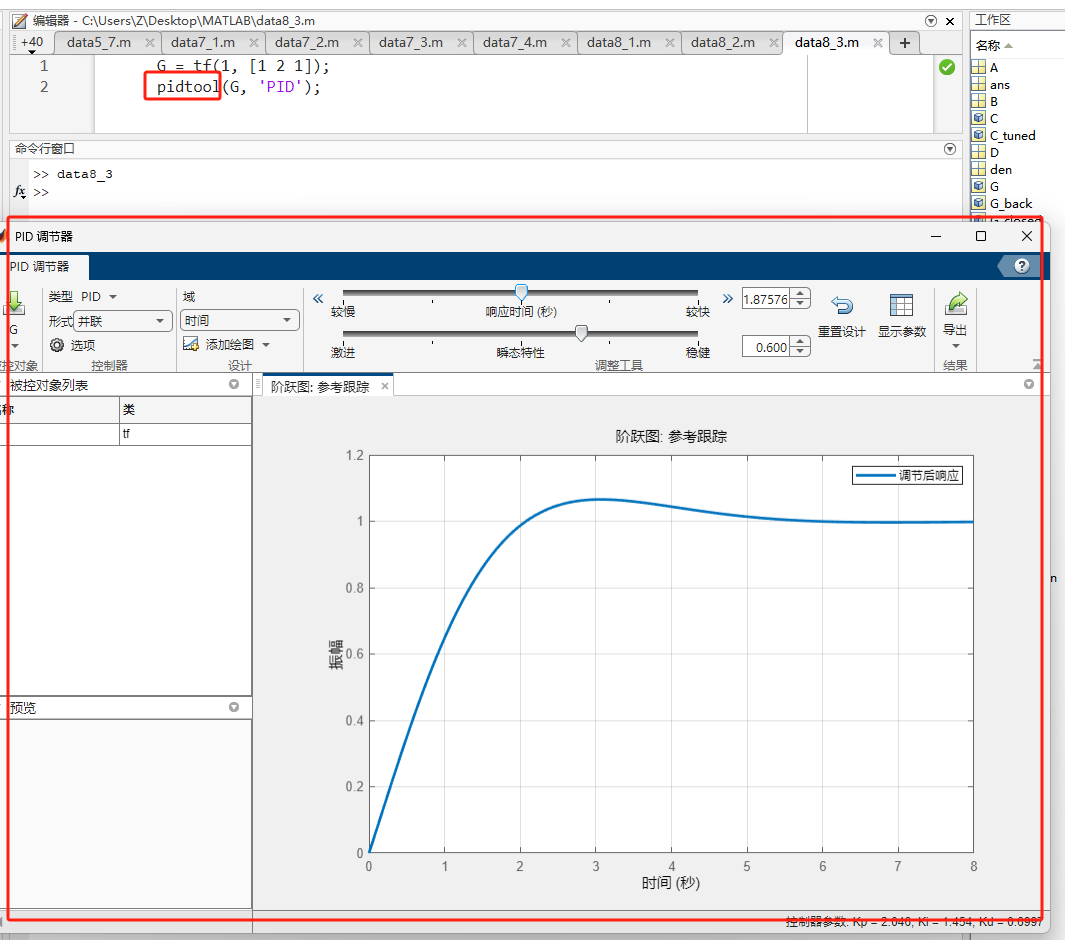
-
功能:打开一个可视化窗口,通过拉动滑块实时改变"响应速度"和"鲁棒性",观察波形变化。
-
输入 :受控对象
G。 -
代码调用 :
matlabG = tf(1, [1 2 1]); pidtool(G, 'PID');
三、 必会 Simulink 模块详解
在 Simulink 中实现 PID,你必须掌握这个"万能模块":
| 模块名称 | 所在库 | 功能讲解与用处 |
|---|---|---|
| PID Controller | Continuous | 功能 :集成了 P、I、D 以及 微分滤波 和 抗积分饱和(Anti-windup)。 |
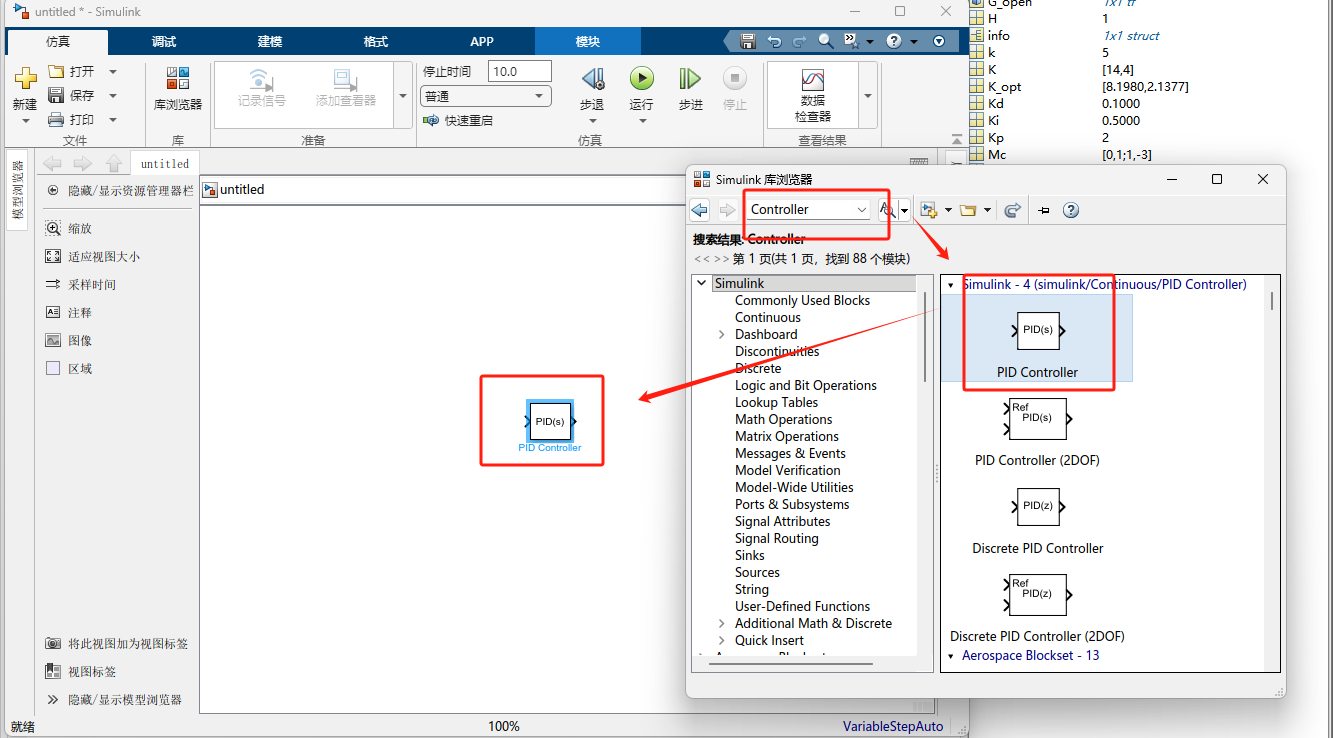
🔍 Simulink 模块深度教程:
-
双击模块进入设置:
Controller:选择 PID、PI 或 P。Form:选 Parallel(并联)或 Ideal(理想型)。Time Domain:选 Continuous(连续)或 Discrete(离散)。
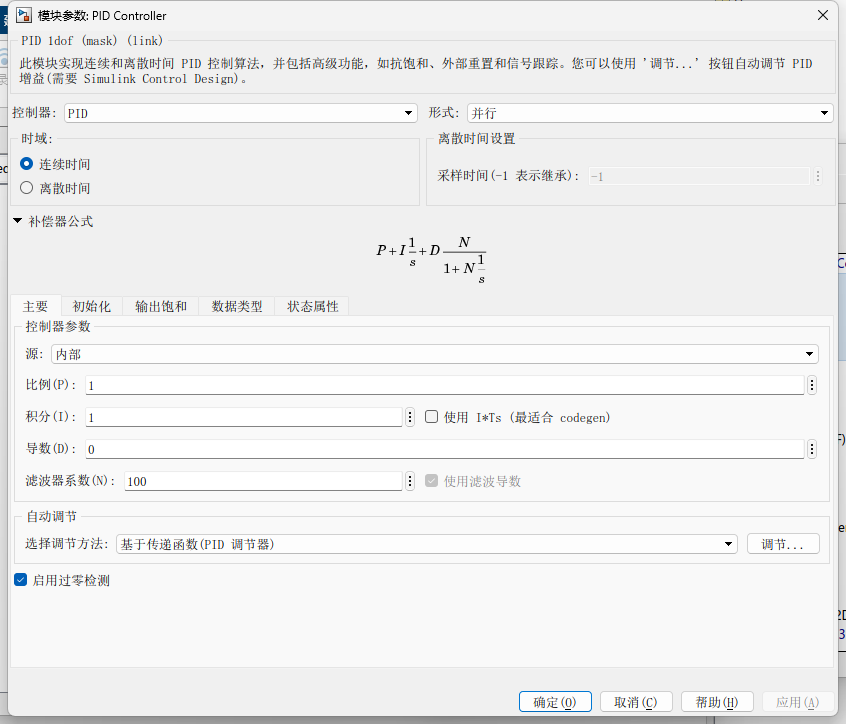
-
微分环节的陷阱 :在现实中,纯微分会放大高频噪声。你会看到一个
Filter coefficient (N),这其实是一个低通滤波器。通常设为 10~100。 -
抗积分饱和(重要) :切换到
Output Saturation标签,勾选Limit output。这样当执行机构(如阀门)开到最大时,积分器会停止累积,防止系统产生剧烈震荡。 -
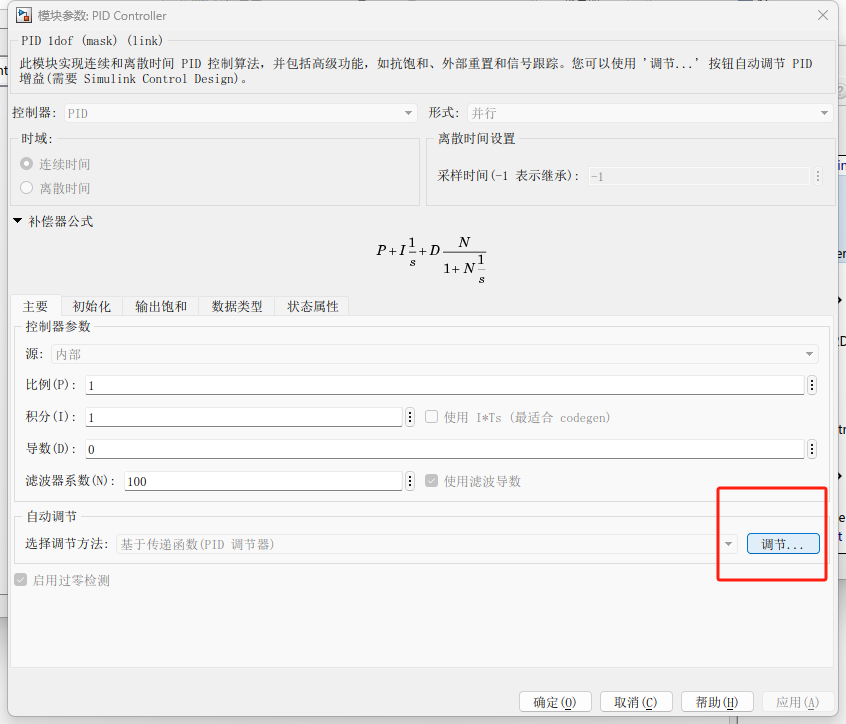
模块内的 Tune 按钮 :双击模块后,点击那个蓝色的
Tune...按钮。它会自动运行pidtool的图形化界面,调好后点Update Block,参数就自动填好了。
四、 阶段性综合实战 (Milestone 4)
项目:恒温控制系统的 PID 整定
受控对象 :一个具有大滞后的加热炉模型 G ( s ) = 1 ( s + 1 ) 2 e − 0.5 s G(s) = \frac{1}{(s+1)^2} e^{-0.5s} G(s)=(s+1)21e−0.5s。
任务:
- 利用 Pade 近似处理时滞。
- 使用
pidtune自动设计 PID 控制器。 - 在 Simulink 中搭建闭环系统,观察加入"抗饱和"前后的区别。
MATLAB 设计脚本:
matlab
%% 1. 建模(处理滞后)
G_no_delay = tf(1, [1 2 1]);
G = G_no_delay;
G.IODelay = 0.5; % 设置 0.5s 的时间滞后
%% 2. 自动整定
[C, info] = pidtune(G, 'PID');
fprintf('整定出的参数:Kp=%.2f, Ki=%.2f, Kd=%.2f\n', C.Kp, C.Ki, C.Kd);
%% 3. 验证性能
sys_cl = feedback(C*G, 1);
step(sys_cl); grid on;
title('自动整定后的恒温系统阶跃响应');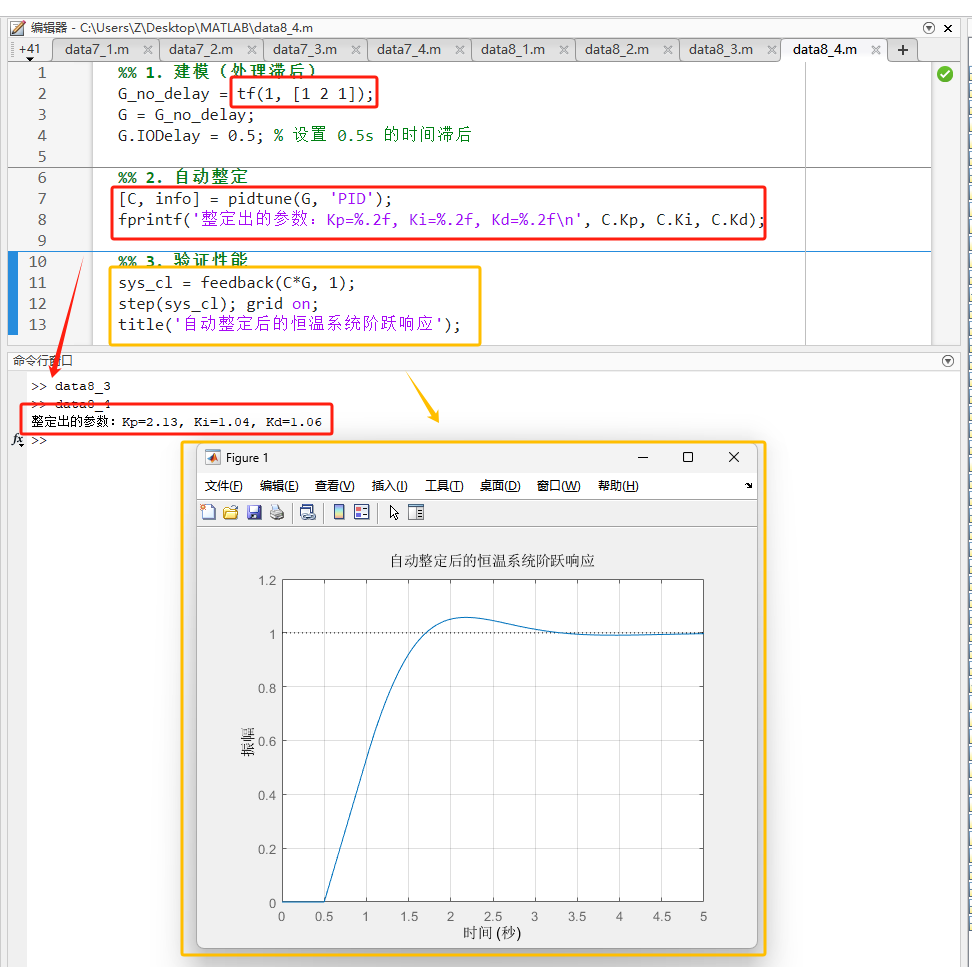
这个实验展示了工业控制中极其重要的**抗积分饱和(Anti-windup)**概念。在实际硬件中,执行器(如阀门开度、电机电压)都有极限,如果不加限制,PID 的积分项会由于误差持续积累而变得巨大,导致系统在回到稳态时产生巨大的超调或振荡。
以下是手把手的搭建过程:
Simulink建模过程:
第一步:打开 Simulink 并新建模型
- 在 MATLAB 命令行输入
simulink并回车。 - 点击 Blank Model 创建一个空白画布。
第二步:搭建受控对象(Plant)
由于我们要对比,建议先做一个通用的"受控对象"子系统,或者直接复制两份。
- Transport Delay (传输延迟):
- 在库浏览器搜索
Transport Delay拖入。 - 双击设置:
Time delay改为0.5。
- 在库浏览器搜索
- Transfer Fcn (传递函数):
- 搜索
Transfer Fcn拖入,连在延迟模块后面。 - 双击设置:
Numerator coefficients为[1],Denominator coefficients为[1 1](即 1 / ( s + 1 ) 1/(s+1) 1/(s+1))。
- 搜索
- 组合 :将这两个模块串联。为了方便,你可以选中它们,按
Ctrl+G封装成一个 Subsystem,命名为 "Object"。
第三步:搭建回路 A(无限制对比组)
- Step (阶跃信号):搜索
Step。双击设置:Step time为1,Final value为2(故意设大一点,让它触碰极限)。 - Sum (误差计算):搜索
Sum。双击将符号改为+-。将 Step 连接到+。 - PID Controller :搜索
PID Controller。连接到 Sum 后面。- 参数设置 :双击进入,
Controller选PID。 - 建议参数:
P=2,I=1,D=0.1(不要用默认的,容易看不出效果)。 - 关键点 :此时点击 PID Advanced 选项卡,确认 Output saturation 下的
Limit output是 未勾选 的。
- 参数设置 :双击进入,
- 连接受控对象:将 PID 输出接到第二步建好的 "Object" 输入。
- 反馈 :将 "Object" 的输出连回 Sum 的
-端。
第四步:搭建回路 B(带限幅和抗饱和)
- 整体复制:直接选中回路 A 的所有模块,按住右键拖动,复制出一套一模一样的在下方。
- 修改 PID B 参数 :
- 双击回路 B 的 PID 模块。
- 点击 Output saturation 选项卡。
- 勾选 Limit output。
- 设置 Upper limit 为
1,Lower limit 为-1。 - 点击 PID Advanced 选项卡。
- 在 Anti-windup method (抗饱和方法)下拉菜单中选择 clamping(这是最常用的"钳位"法)。
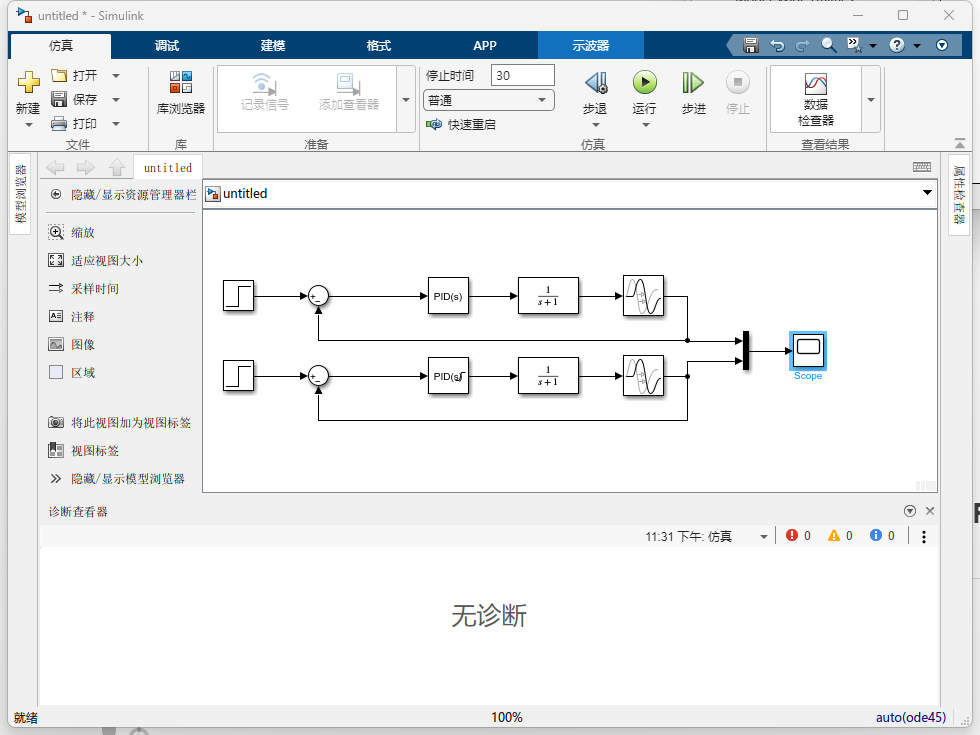
第五步:观察结果(Scope)
- Mux (信号合并):搜索
Mux,双击将Number of inputs改为3。 - Scope (示波器):搜索
Scope,连在 Mux 后面。 - 连线 :
- Mux 输入 1:接顶部的 Step 信号(作为参考基准)。
- Mux 输入 2:接 回路 A 受控对象的输出。
- Mux 输入 3:接 回路 B 受控对象的输出。
- 运行 :将顶部的仿真时间从
10.0改为30.0,点击绿色的 Run 按钮。
第六步:你会看到什么?(核心逻辑)
在 Scope 窗口中,你会观察到:
- 回路 A(黄色/蓝色线) :由于 PID 内部没有限幅,它的计算输出可能会达到 10 甚至更高。即使受控对象其实已经"吃不消"了,积分项仍在疯狂累加(积分饱和)。当反馈值快要追上给定值时,由于积分项太大,它掉不头,导致系统产生巨大的超调(Overshoot),甚至剧烈震荡。
- 回路 B(另一色线) :
- 限幅作用 :PID 的输出被死死限制在
[-1, 1]之间,模拟了真实电机的最大电压或阀门的最大开度。 - 抗饱和作用 :由于开启了
Anti-windup,当输出达到1时,内部积分器会停止累加。当误差开始减小时,回路 B 能立即做出反应开始回撤。 - 结果 :你会发现回路 B 的上升曲线虽然在初期受限于功率比 A 慢一点,但它到达目标值时非常平稳,几乎没有超调 。
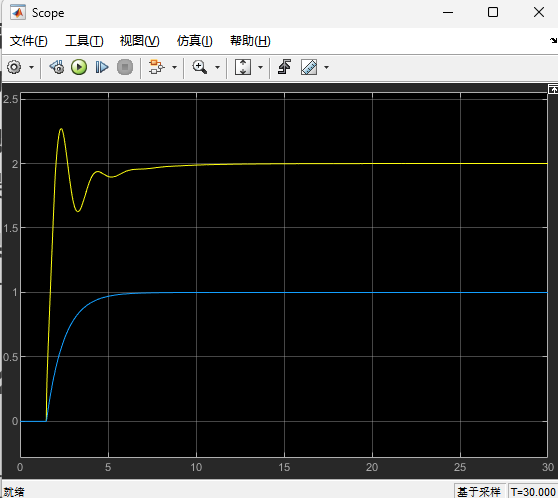
- 限幅作用 :PID 的输出被死死限制在
总结:为什么要这么连?
在工业现场,没有不带限幅的执行器。"PID + 输出限幅 + 抗饱和" 是工业控制器的标配。通过这个对比,你直观地看到了如果不处理积分饱和,数学上的"最优"在实际物理限制下会变得多么糟糕。
五、 第八章 语法与编程注意点
C.Kp,C.Ki的访问 :PID 对象C是一个结构化对象,你可以直接通过.操作符读取或修改具体的参数。- 离散化 :如果你的控制器要写进单片机,记得用
c2d(C, Ts, 'tustin')将 PID 对象离散化。 - Pade 近似 :
[num, den] = pade(0.5, 2),可以用二阶多项式来近似表示 0.5s 的纯滞后,这对某些只支持多项式的分析函数很有用。
复习建议
- 掌握一个技能 :学会使用
pidtune。它能节省你 90% 的调试时间。 - 理解一个概念 :为什么微分环节要加 Filter (N)?(因为噪声是控制系统的敌人)。
PID 是经典控制的终点。如果你已经玩转了 PID,那么恭喜你,你已经具备了解决 90% 实际工程问题的能力。