一、功能概述
该算子基于霍夫变换(Hough Transform)原理,从边缘图像中提取直线段,并计算每条线段的方向(角度)。
二、算子解释
cpp
hough_lines_dir(Edges : Lines : AngleResolution, Threshold, MinLineLength, MaxLineGap, Smoothing, LineLength, LineGap : )
输入参数:
Edges(输入对象)
输入边缘图像(通常由 edges_sub_pix 等算子得到)。
AngleResolution(输入控制)
角度分辨率(弧度)。例如 pi/180 表示 1 度步进。值越小,检测越精确但计算量越大。
Threshold(输入控制)
霍夫空间累加器阈值。值越高,只检测越明显的直线。
MinLineLength(输入控制)
最小线段长度(像素)。短于此长度的线段会被忽略。
MaxLineGap(输入控制)
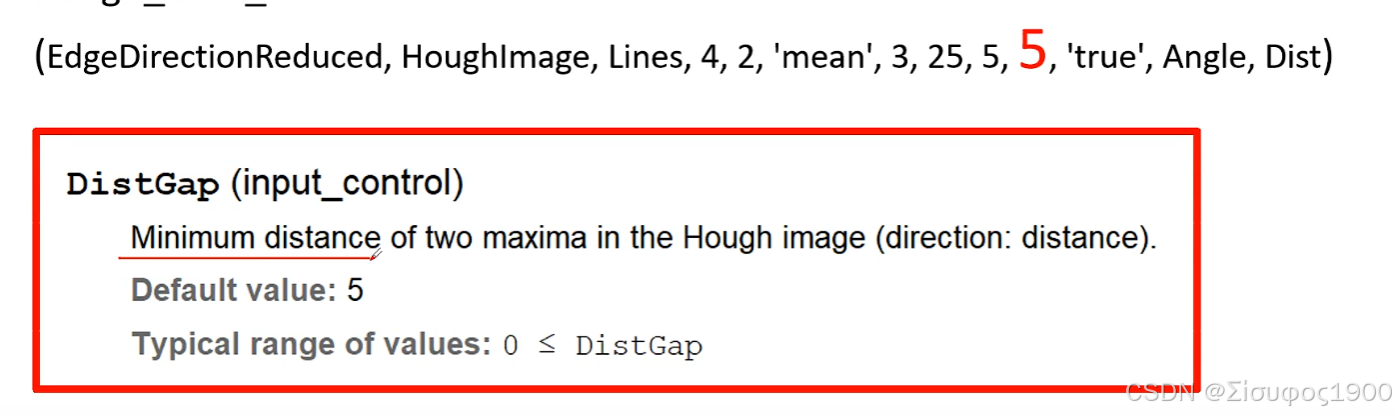
允许的最大线段间断(像素)。间断小于此值的线段会被连接成一条直线。
Smoothing(输入控制)
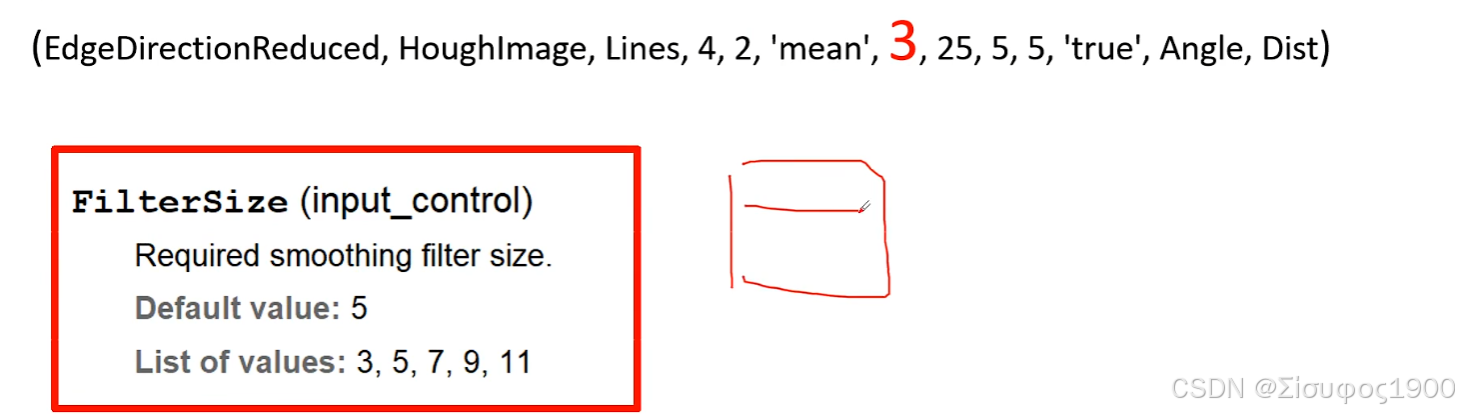
边缘方向平滑参数(通常取奇数,如 3、5、7)。值越大,方向估计越平滑。
LineLength(输入控制)
输出线段的最小长度(像素)。
LineGap(输入控制)
同一直线上允许的最大间隙(像素)。
输出参数:
Lines(输出对象)
检测到的直线段集合,每个线段用两端点坐标表示。
Angle(输出控制)
每条线段的方向角度(弧度),范围通常为 [-π/2, π/2]。



三、案例介绍
cpp
* Detect lines in an image with the help of the Hough transform
* using the edge direction as additional information and return it both
* in HNF and as regions
*
read_image (Image, 'fabrik')
rectangle1_domain (Image, ImageReduced, 170, 280, 310, 360)
* Detect edges (amplitude and direction) using the Sobel operator
sobel_dir (ImageReduced, EdgeAmplitude, EdgeDirection, 'sum_abs', 3)
dev_set_color ('red')
threshold (EdgeAmplitude, Region, 55, 255)
* Reduce the direction image to the edge region
reduce_domain (EdgeDirection, Region, EdgeDirectionReduced)
* Start the Hough transform using the edge direction information
hough_lines_dir (EdgeDirectionReduced, HoughImage, Lines, 4, 2, 'mean', 3, 50, 5, 5, 'true', Angle, Dist)
* Store input lines described in HNF
gen_region_hline (LinesHNF, Angle, Dist)
dev_display (Image)
dev_set_colored (12)
* Display the lines
dev_set_draw ('margin')
dev_display (LinesHNF)
* Display the edge pixels that contributed to the corresponding lines
dev_set_draw ('fill')
dev_display (Lines)选出区域

hough 变化结果


四、原理
直线霍夫变换的本质推导是:
把"点是否共线"的几何判定转化为"参数空间中函数族是否相交"的问题再通过离散化将其变成峰值检测
问题的数学本质

为什么不用 y=kx+b(推导动机)

核心推导:点 → 参数空间约束
1️⃣ 固定一个图像点

2️⃣ 几何解释(关键)
-
图像空间:一个点
-
参数空间:一条曲线
这不是技巧,是严格的集合映射:
图像点 PPP
⟶ 所有包含 PPP 的直线集合
⟶ 参数空间中的一维流形
共线性的数学等价转化(关键定理)
假设:

离散化:从连续推导到算法
1️⃣ 参数空间量化
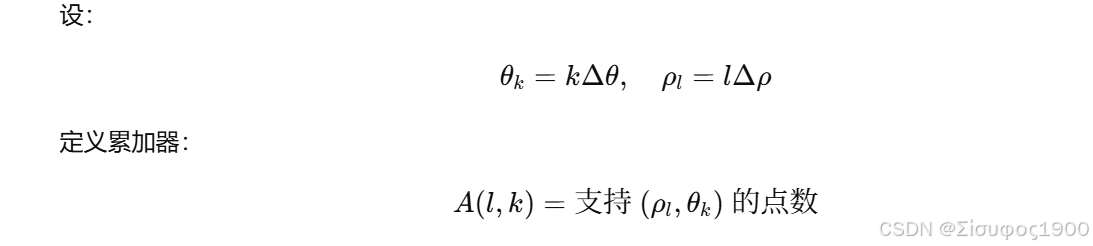
2️⃣ 投票的数学形式
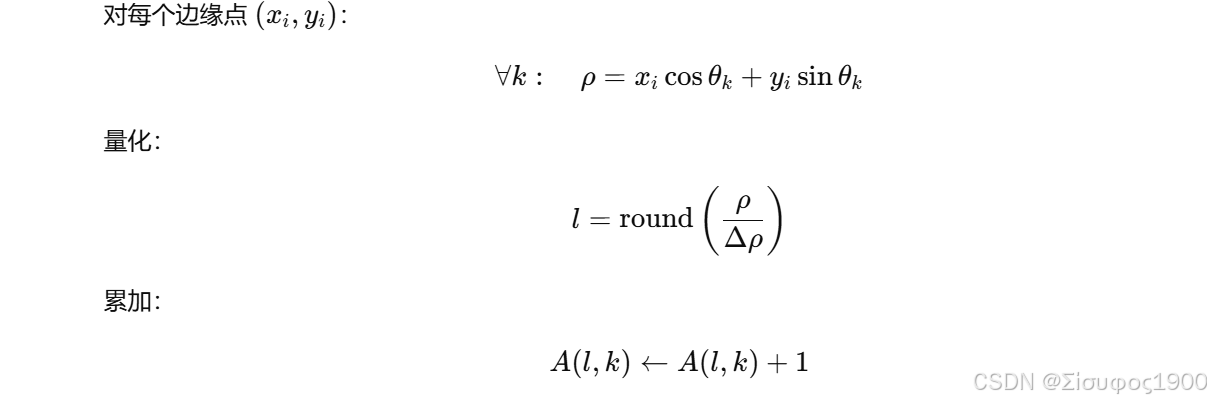
3️⃣ 峰值检测 = 极大似然

与 RANSAC 的严格关系
| 方法 | 本质 |
|---|---|
| 霍夫 | 在参数空间做全局穷举投票 |
| RANSAC | 在数据空间做随机模型采样 |
| 代价函数 | 0-1 一致性 |
| 目标 | 最大内点数 |
所以你会发现:
霍夫是确定性的 RANSAC
RANSAC 是随机化的霍夫
五、霍夫在亚像素精度下为什么不靠谱
霍夫变换在亚像素精度下不靠谱,不是实现问题,而是数学建模层面"先天不足"。
霍夫变换在亚像素精度下不靠谱,不是因为实现不够好,而是因为它的误差函数是离散、不可微、量化受限的,先天不具备连续优化所需的统计与几何结构。
下面我从 4 个严格原因 + 数学解释 + 工程后果 一层层拆。
第一性原因:参数空间"量化误差"是结构性的
a、霍夫本质是离散优化
霍夫不是在解连续问题:

b、量化误差下界

第二性原因:误差函数是"平顶"的(不可微)

第三性原因:峰值不是"点",而是一片"脊"

第四性原因:噪声不是高斯,统计模型不成立

用公式直观对比一下(关键)
