要得到散射矩阵 [S][S][S] 的显式表达式,需从传输矩阵[A][A][A] 出发,利用电压电流与入射波、反射波的关系进行推导。假设四端口网络对称且各端口特性阻抗相同(均为 Z0=Z0eZ0oZ_0 = \sqrt{Z_{0e} Z_{0o}}Z0=Z0eZ0o ),推导过程如下。
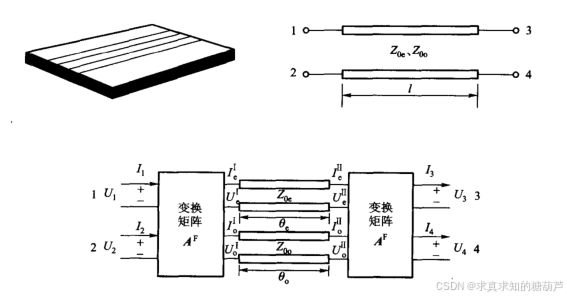
图1 简明微波耦合线四端口分析
上一节我们由图1推出了耦合微带线的A参数矩阵,下面来推导Z参数矩阵
1. 对称均匀耦合线的A参数矩阵为:
A=[cosθ0j12(Z0e+Z0o)sinθj12(Z0e−Z0o)sinθ0cosθj12(Z0e−Z0o)sinθj12(Z0e+Z0o)sinθj12(1Z0e+1Z0o)sinθj12(1Z0e−1Z0o)sinθcosθ0j12(1Z0e−1Z0o)sinθj12(1Z0e+1Z0o)sinθ0cosθ] A = \begin{bmatrix} \cos\theta & 0 & j\frac{1}{2}(Z_{0e}+Z_{0o})\sin\theta & j\frac{1}{2}(Z_{0e}-Z_{0o})\sin\theta \\ 0 & \cos\theta & j\frac{1}{2}(Z_{0e}-Z_{0o})\sin\theta & j\frac{1}{2}(Z_{0e}+Z_{0o})\sin\theta \\ j\frac{1}{2}\left(\frac{1}{Z_{0e}}+\frac{1}{Z_{0o}}\right)\sin\theta & j\frac{1}{2}\left(\frac{1}{Z_{0e}}-\frac{1}{Z_{0o}}\right)\sin\theta & \cos\theta & 0 \\ j\frac{1}{2}\left(\frac{1}{Z_{0e}}-\frac{1}{Z_{0o}}\right)\sin\theta & j\frac{1}{2}\left(\frac{1}{Z_{0e}}+\frac{1}{Z_{0o}}\right)\sin\theta & 0 & \cos\theta \end{bmatrix} A= cosθ0j21(Z0e1+Z0o1)sinθj21(Z0e1−Z0o1)sinθ0cosθj21(Z0e1−Z0o1)sinθj21(Z0e1+Z0o1)sinθj21(Z0e+Z0o)sinθj21(Z0e−Z0o)sinθcosθ0j21(Z0e−Z0o)sinθj21(Z0e+Z0o)sinθ0cosθ
该矩阵描述四端口网络的电压-电流关系:(3、4端口电流方向图1中是选择朝外,我们这里为统一计算Z参数改成朝内即给上集我们推导的3、4端口电流向量加负号)
U1U2I1I2\]=A\[U3U4−I3−I4\] \\begin{bmatrix} U_1 \\\\ U_2 \\\\ I_1 \\\\ I_2 \\end{bmatrix} = A \\begin{bmatrix} U_3 \\\\ U_4 \\\\ -I_3 \\\\ -I_4 \\end{bmatrix} U1U2I1I2 =A U3U4−I3−I4 Z参数矩阵,其定义为: \[U12U34\]=Z\[I12I34\] \\begin{bmatrix} \\mathbf{U}_{12} \\\\ \\mathbf{U}_{34} \\end{bmatrix} = Z \\begin{bmatrix} \\mathbf{I}_{12} \\\\ \\mathbf{I}_{34} \\end{bmatrix} \[U12U34\]=Z\[I12I34
其中:
- U12=[U1U2]\mathbf{U}{12} = \begin{bmatrix} U_1 \\ U_2 \end{bmatrix}U12=[U1U2], U34=[U3U4]\mathbf{U}{34} = \begin{bmatrix} U_3 \\ U_4 \end{bmatrix}U34=[U3U4]
- I12=[I1I2]\mathbf{I}{12} = \begin{bmatrix} I_1 \\ I_2 \end{bmatrix}I12=[I1I2], I34=[I3I4]\mathbf{I}{34} = \begin{bmatrix} I_3 \\ I_4 \end{bmatrix}I34=[I3I4]
2. 推导
2.1 A矩阵分块表示
将A矩阵分块为2×2子矩阵:
A=[ABCD] A = \begin{bmatrix} \mathbf{A} & \mathbf{B} \\ \mathbf{C} & \mathbf{D} \end{bmatrix} A=[ACBD]
其中子矩阵为:
A=cosθ[1001],D=cosθ[1001] \mathbf{A} = \cos\theta \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad \mathbf{D} = \cos\theta \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} A=cosθ[1001],D=cosθ[1001]
B=jsinθ2[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o] \mathbf{B} = j\frac{\sin\theta}{2} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} B=j2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
C=jsinθ2[1Z0e+1Z0o1Z0e−1Z0o1Z0e−1Z0o1Z0e+1Z0o] \mathbf{C} = j\frac{\sin\theta}{2} \begin{bmatrix} \frac{1}{Z_{0e}}+\frac{1}{Z_{0o}} & \frac{1}{Z_{0e}}-\frac{1}{Z_{0o}} \\ \frac{1}{Z_{0e}}-\frac{1}{Z_{0o}} & \frac{1}{Z_{0e}}+\frac{1}{Z_{0o}} \end{bmatrix} C=j2sinθ[Z0e1+Z0o1Z0e1−Z0o1Z0e1−Z0o1Z0e1+Z0o1]
2.2 建立方程关系
由A矩阵定义可得:
U12=AU34+B(−I34)(1) \mathbf{U}{12} = \mathbf{A} \mathbf{U}{34} + \mathbf{B} (-\mathbf{I}_{34}) \quad (1) U12=AU34+B(−I34)(1)
I12=CU34+D(−I34)(2) \mathbf{I}{12} = \mathbf{C} \mathbf{U}{34} + \mathbf{D} (-\mathbf{I}_{34}) \quad (2) I12=CU34+D(−I34)(2)
Z矩阵的标准形式为:
U12=Z11I12+Z12(I34)(3) \mathbf{U}{12} = Z{11} \mathbf{I}{12} + Z{12} (\mathbf{I}_{34}) \quad (3) U12=Z11I12+Z12(I34)(3)
U34=Z21I12+Z22(I34)(4) \mathbf{U}{34} = Z{21} \mathbf{I}{12} + Z{22} (\mathbf{I}_{34}) \quad (4) U34=Z21I12+Z22(I34)(4)
2.3 消去中间变量
由方程(2)解出 U34\mathbf{U}_{34}U34(假设 C\mathbf{C}C 可逆):
I12=CU34−DI34 \mathbf{I}{12} = \mathbf{C} \mathbf{U}{34} - \mathbf{D} \mathbf{I}_{34} I12=CU34−DI34
CU34=I12+DI34 \mathbf{C} \mathbf{U}{34} = \mathbf{I}{12} + \mathbf{D} \mathbf{I}_{34} CU34=I12+DI34
U34=C−1I12+C−1DI34(5) \mathbf{U}{34} = \mathbf{C}^{-1} \mathbf{I}{12} + \mathbf{C}^{-1} \mathbf{D} \mathbf{I}_{34} \quad (5) U34=C−1I12+C−1DI34(5)
将(5)代入(1):
U12=A[C−1I12+C−1DI34]−BI34 \mathbf{U}{12} = \mathbf{A} [\mathbf{C}^{-1} \mathbf{I}{12} + \mathbf{C}^{-1} \mathbf{D} \mathbf{I}{34}] - \mathbf{B} \mathbf{I}{34} U12=A[C−1I12+C−1DI34]−BI34
U12=AC−1I12+[AC−1D−B]I34(6) \mathbf{U}{12} = \mathbf{A} \mathbf{C}^{-1} \mathbf{I}{12} + [\mathbf{A} \mathbf{C}^{-1} \mathbf{D} - \mathbf{B}] \mathbf{I}_{34} \quad (6) U12=AC−1I12+[AC−1D−B]I34(6)
对比方程(3)和(6),可得:
Z11=AC−1,Z12=AC−1D−B Z_{11} = \mathbf{A} \mathbf{C}^{-1}, \quad Z_{12} =\mathbf{A} \mathbf{C}^{-1} \mathbf{D}- \mathbf{B} Z11=AC−1,Z12=AC−1D−B
由方程(5)对比方程(4),可得:
Z21=C−1,Z22=C−1D Z_{21} = \mathbf{C}^{-1}, \quad Z_{22} = \mathbf{C}^{-1} \mathbf{D} Z21=C−1,Z22=C−1D
因此,Z矩阵的完整形式为:
Z=[AC−1AC−1D−BC−1C−1D](7) Z = \begin{bmatrix} \mathbf{A} \mathbf{C}^{-1} &\mathbf{A} \mathbf{C}^{-1} \mathbf{D}- \mathbf{B} \\ \mathbf{C}^{-1} & \mathbf{C}^{-1} \mathbf{D} \end{bmatrix} \quad (7) Z=[AC−1C−1AC−1D−BC−1D](7)
2.4. 计算 C−1\mathbf{C}^{-1}C−1
定义 ye=1Z0ey_e = \frac{1}{Z_{0e}}ye=Z0e1, yo=1Z0oy_o = \frac{1}{Z_{0o}}yo=Z0o1,则:
C=jsinθ2[ye+yoye−yoye−yoye+yo] \mathbf{C} = j\frac{\sin\theta}{2} \begin{bmatrix} y_e+y_o & y_e-y_o \\ y_e-y_o & y_e+y_o \end{bmatrix} C=j2sinθ[ye+yoye−yoye−yoye+yo]
令 k=jsinθ2k = j\frac{\sin\theta}{2}k=j2sinθ, a=ye+yoa = y_e+y_oa=ye+yo, b=ye−yob = y_e-y_ob=ye−yo,则:
C=k[abba] \mathbf{C} = k \begin{bmatrix} a & b \\ b & a \end{bmatrix} C=k[abba]
逆矩阵为:
C−1=1k⋅1a2−b2[a−b−ba] \mathbf{C}^{-1} = \frac{1}{k} \cdot \frac{1}{a^2 - b^2} \begin{bmatrix} a & -b \\ -b & a \end{bmatrix} C−1=k1⋅a2−b21[a−b−ba]
计算 a2−b2=(ye+yo)2−(ye−yo)2=4yeyo=4Z0eZ0oa^2 - b^2 = (y_e+y_o)^2 - (y_e-y_o)^2 = 4y_e y_o = \frac{4}{Z_{0e}Z_{0o}}a2−b2=(ye+yo)2−(ye−yo)2=4yeyo=Z0eZ0o4
代入 k−1=−j2sinθk^{-1} = -j\frac{2}{\sin\theta}k−1=−jsinθ2:
C−1=−j2sinθ⋅Z0eZ0o4[a−b−ba]=−jZ0eZ0o2sinθ[a−b−ba] \mathbf{C}^{-1} = -j\frac{2}{\sin\theta} \cdot \frac{Z_{0e}Z_{0o}}{4} \begin{bmatrix} a & -b \\ -b & a \end{bmatrix} = \frac{-j Z_{0e}Z_{0o}}{2\sin\theta} \begin{bmatrix} a & -b \\ -b & a \end{bmatrix} C−1=−jsinθ2⋅4Z0eZ0o[a−b−ba]=2sinθ−jZ0eZ0o[a−b−ba]
带入中间变量 a,ba,ba,b 表达式:
a=ye+yo=Z0e+Z0oZ0eZ0o,b=ye−yo=Z0e−Z0oZ0eZ0o a = y_e+y_o = \frac{Z_{0e}+Z_{0o}}{Z_{0e}Z_{0o}}, \quad b = y_e-y_o = \frac{Z_{0e}-Z_{0o}}{Z_{0e}Z_{0o}} a=ye+yo=Z0eZ0oZ0e+Z0o,b=ye−yo=Z0eZ0oZ0e−Z0o
得:
C−1=−j2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o](8) \mathbf{C}^{-1} = \frac{-j}{2\sin\theta} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} \quad (8) C−1=2sinθ−j[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o](8)
2.5. 计算Z矩阵各分块
2.5.1 计算 Z21Z_{21}Z21 和 Z22Z_{22}Z22
由(7)式和(8)式直接可得:
Z21=C−1=−j2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o] Z_{21} = \mathbf{C}^{-1} = \frac{-j}{2\sin\theta} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} Z21=C−1=2sinθ−j[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
Z22=C−1D=C−1(cosθI)=−jcosθ2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o] Z_{22} = \mathbf{C}^{-1} \mathbf{D} = \mathbf{C}^{-1} (\cos\theta \mathbf{I}) = -\frac{j\cos\theta}{2\sin\theta} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} Z22=C−1D=C−1(cosθI)=−2sinθjcosθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
2.5.2 计算 Z11Z_{11}Z11 和 Z12Z_{12}Z12
Z11=AC−1=cosθC−1=−jcosθ2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o] Z_{11} = \mathbf{A} \mathbf{C}^{-1} = \cos\theta \mathbf{C}^{-1} = \frac{-j\cos\theta}{2\sin\theta} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} Z11=AC−1=cosθC−1=2sinθ−jcosθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
简化计算定义矩阵 M=[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]\mathbf{M} = \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix}M=[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
则:
- B=jsinθ2M\mathbf{B} = j\frac{\sin\theta}{2} \mathbf{M}B=j2sinθM
- C−1=−j2sinθM\mathbf{C}^{-1} = \frac{-j}{2\sin\theta} \mathbf{M}C−1=2sinθ−jM
- AC−1D=cosθZ11=−jcos2θ2sinθM\mathbf{A} \mathbf{C}^{-1} \mathbf{D} = \cos\theta Z_{11} = \frac{-j\cos^2\theta}{2\sin\theta} \mathbf{M}AC−1D=cosθZ11=2sinθ−jcos2θM
因此:
Z12=AC−1D−B=−jcos2θ2sinθM−jsinθ2M=−jsin2θ+cos2θ2sinθM=−j2sinθM Z_{12} = \mathbf{A} \mathbf{C}^{-1} \mathbf{D} - \mathbf{B} =- j\frac{\cos^2\theta}{2\sin\theta} \mathbf{M}- j\frac{\sin\theta}{2} \mathbf{M} = -j\frac{\sin^2\theta + \cos^2\theta}{2\sin\theta} \mathbf{M} = -\frac{j}{2\sin\theta} \mathbf{M} Z12=AC−1D−B=−j2sinθcos2θM−j2sinθM=−j2sinθsin2θ+cos2θM=−2sinθjM
即:
Z12=−j2sinθ[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o] Z_{12} =- \frac{j}{2\sin\theta} \begin{bmatrix} Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \end{bmatrix} Z12=−2sinθj[Z0e+Z0oZ0e−Z0oZ0e−Z0oZ0e+Z0o]
3、最终Z参数矩阵
综合以上结果,完整的4×4 Z参数矩阵为:
Z=−j2sinθ[cosθMMMcosθM] Z = -\frac{j}{2\sin\theta} \begin{bmatrix} \cos\theta \mathbf{M} & \mathbf{M} \\ \mathbf{M} & \cos\theta \mathbf{M} \end{bmatrix} Z=−2sinθj[cosθMMMcosθM]
展开 M\mathbf{M}M 矩阵,得到最终结果:
Z=−j2sinθ[cosθ(Z0e+Z0o)cosθ(Z0e−Z0o)Z0e+Z0oZ0e−Z0ocosθ(Z0e−Z0o)cosθ(Z0e+Z0o)Z0e−Z0oZ0e+Z0o(Z0e+Z0o)(Z0e−Z0o)cosθ(Z0e+Z0o)cosθ(Z0e−Z0o)(Z0e−Z0o)(Z0e+Z0o)cosθ(Z0e−Z0o)cosθ(Z0e+Z0o)] \boxed{ Z = \frac{-j}{2\sin\theta} \begin{bmatrix} \cos\theta (Z_{0e}+Z_{0o}) & \cos\theta (Z_{0e}-Z_{0o}) & Z_{0e}+Z_{0o} & Z_{0e}-Z_{0o} \\ \cos\theta (Z_{0e}-Z_{0o}) & \cos\theta (Z_{0e}+Z_{0o}) & Z_{0e}-Z_{0o} & Z_{0e}+Z_{0o} \\ (Z_{0e}+Z_{0o}) & (Z_{0e}-Z_{0o}) & \cos\theta (Z_{0e}+Z_{0o}) & \cos\theta (Z_{0e}-Z_{0o}) \\ (Z_{0e}-Z_{0o}) & (Z_{0e}+Z_{0o}) & \cos\theta (Z_{0e}-Z_{0o}) & \cos\theta (Z_{0e}+Z_{0o}) \end{bmatrix} } Z=2sinθ−j cosθ(Z0e+Z0o)cosθ(Z0e−Z0o)(Z0e+Z0o)(Z0e−Z0o)cosθ(Z0e−Z0o)cosθ(Z0e+Z0o)(Z0e−Z0o)(Z0e+Z0o)Z0e+Z0oZ0e−Z0ocosθ(Z0e+Z0o)cosθ(Z0e−Z0o)Z0e−Z0oZ0e+Z0ocosθ(Z0e−Z0o)cosθ(Z0e+Z0o)
总结一下
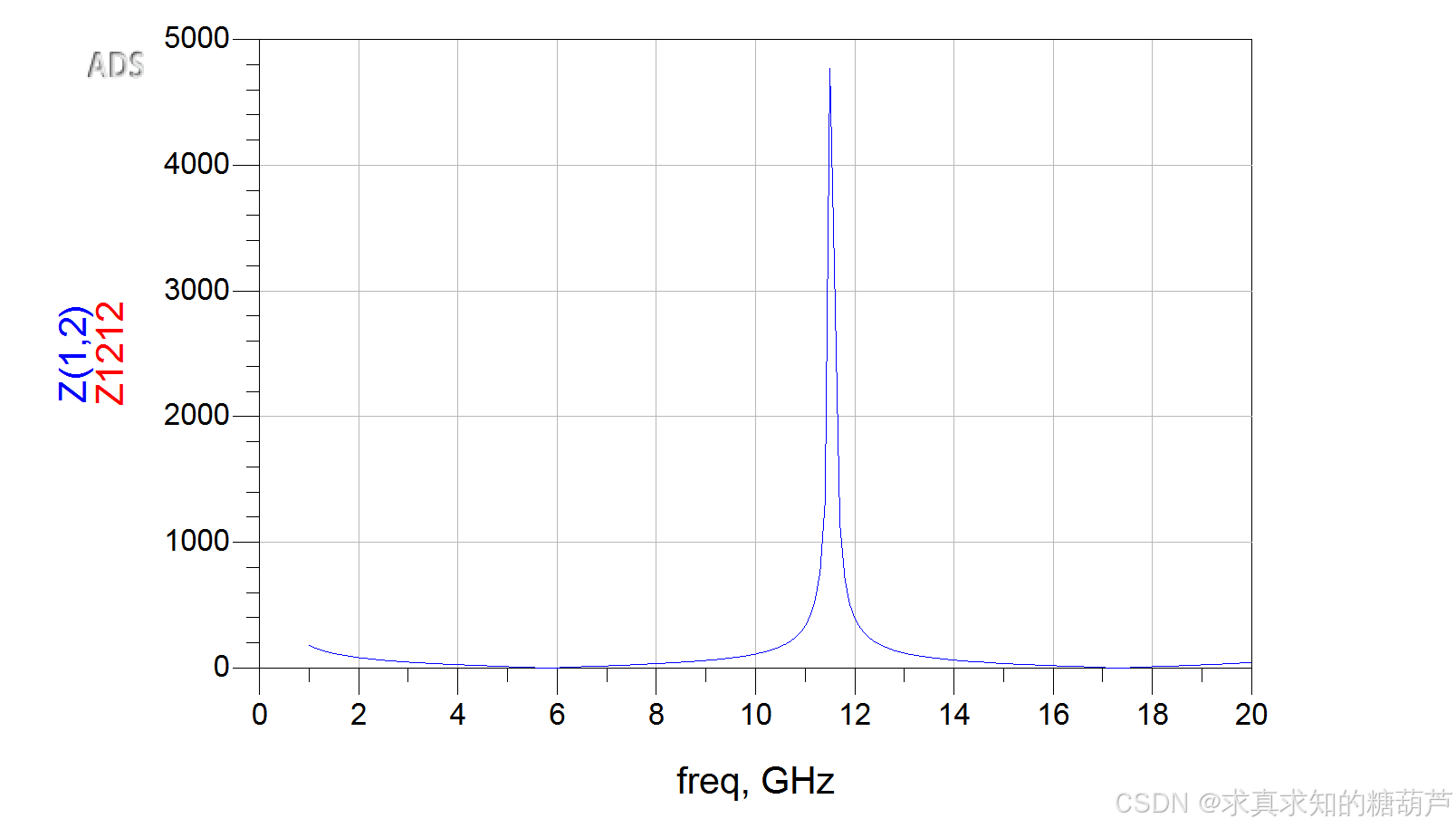
该Z矩阵是对称 的(Zij=ZjiZ_{ij} = Z_{ji}Zij=Zji)可以说明对称均匀耦合线是互易网络,于此同时当 sinθ=0\sin\theta = 0sinθ=0(即电长度 θ=kπ\theta = k\piθ=kπ,kkk为整数)时,矩阵元素趋于无穷大,这对应物理上的谐振点。这里面包含三个变量,偶模阻抗 Z0eZ_{0e}Z0e、奇模阻抗 Z0oZ_{0o}Z0o 和电长度 θ\thetaθ ,系统参考阻抗为Z0=Z0eZ0oZ_0 = \sqrt{Z_{0e} Z_{0o}}Z0=Z0eZ0o 。
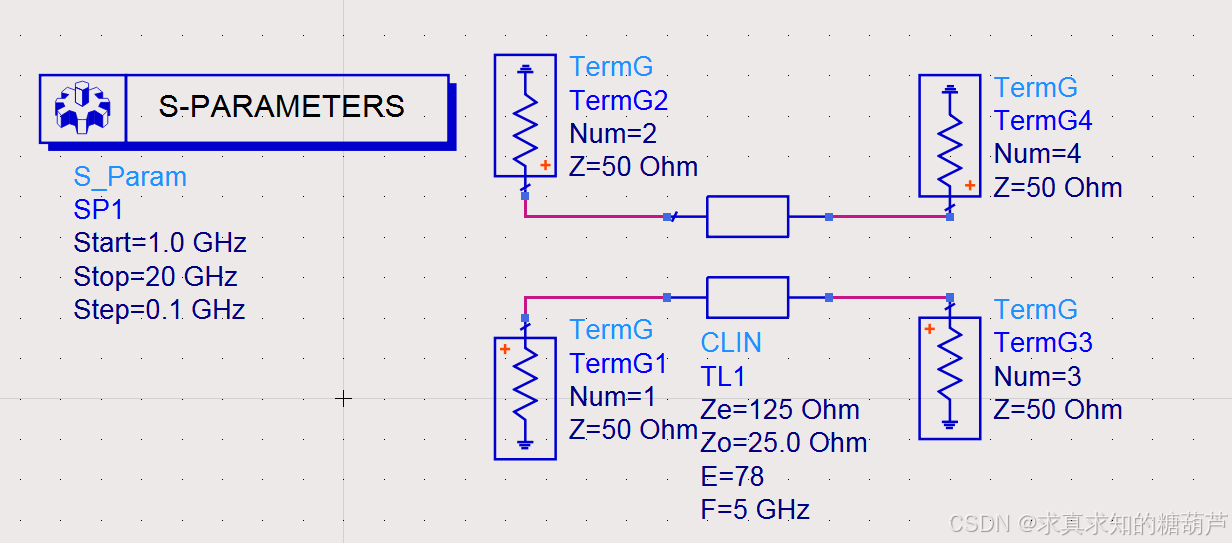
图2 耦合线测试电路
这里我们用图2理想耦合线电路测试一下
勾选参数
求解 θ\thetaθ
利用Z11Z_{11}Z11 和Z13Z_{13}Z13的比值求θ\thetaθ。由矩阵表达式知:
Z11=−jcosθ2sinθ(Z0e+Z0o),Z13=−j2sinθ(Z0e+Z0o) Z_{11} = -\frac{j \cos\theta}{2\sin\theta} (Z_{0e}+Z_{0o}), \quad Z_{13} = -\frac{j}{2\sin\theta} (Z_{0e}+Z_{0o}) Z11=−2sinθjcosθ(Z0e+Z0o),Z13=−2sinθj(Z0e+Z0o)
两式相除得:
Z11Z13=cosθ \frac{Z_{11}}{Z_{13}} = \cos\theta Z13Z11=cosθ
因此:
cosθ=Z11Z13 \cos\theta = \frac{Z_{11}}{Z_{13}} cosθ=Z13Z11
由于无耗网络,Z11Z_{11}Z11和Z13Z_{13}Z13 为纯虚数,其比值为实数。但实际中可能因不理想因素有小实部,可取其虚部比值或直接取比值实部。进而:
θ=arccos(Z11Z13) \theta = \arccos\left(\frac{Z_{11}}{Z_{13}}\right) θ=arccos(Z13Z11)
注意:θ\thetaθ可以取主值范围0≤θ≤π0 \le \theta \le \pi0≤θ≤π,且 sinθ≥0\sin\theta \ge 0sinθ≥0。
求解Z0eZ_{0e}Z0e和 Z0oZ_{0o}Z0o
由Z13Z_{13}Z13和Z14Z_{14}Z14的表达式:
Z13=−j2sinθ(Z0e+Z0o),Z14=−j2sinθ(Z0e−Z0o) Z_{13} = -\frac{j}{2\sin\theta} (Z_{0e}+Z_{0o}), \quad Z_{14} =- \frac{j}{2\sin\theta} (Z_{0e}-Z_{0o}) Z13=−2sinθj(Z0e+Z0o),Z14=−2sinθj(Z0e−Z0o)
可得:
Z0e+Z0o=2jsinθ⋅Z13 Z_{0e}+Z_{0o} = 2j\sin\theta \cdot Z_{13} Z0e+Z0o=2jsinθ⋅Z13
Z0e−Z0o=2jsinθ⋅Z14 Z_{0e}-Z_{0o} = 2j\sin\theta \cdot Z_{14} Z0e−Z0o=2jsinθ⋅Z14
因此:
Z0e=jsinθ⋅(Z13+Z14) Z_{0e} = j\sin\theta \cdot (Z_{13} + Z_{14}) Z0e=jsinθ⋅(Z13+Z14)
Z0o=jsinθ⋅(Z13−Z14) Z_{0o} = j\sin\theta \cdot (Z_{13} - Z_{14}) Z0o=jsinθ⋅(Z13−Z14)
将步骤3求得的sinθ=1−cos2θ\sin\theta = \sqrt{1 - \cos^2\theta}sinθ=1−cos2θ 代入即可。
进行交叉验证:
Z12=−jcosθ2sinθ(Z0e−Z0o) Z_{12} = -\frac{j\cos\theta}{2\sin\theta}(Z_{0e}-Z_{0o}) Z12=−2sinθjcosθ(Z0e−Z0o)
将求得的参数代入,检查是否与原始Z12Z_{12}Z12一致。
将上述公式输入ADS

奇偶模阻抗计算结果与设定一致
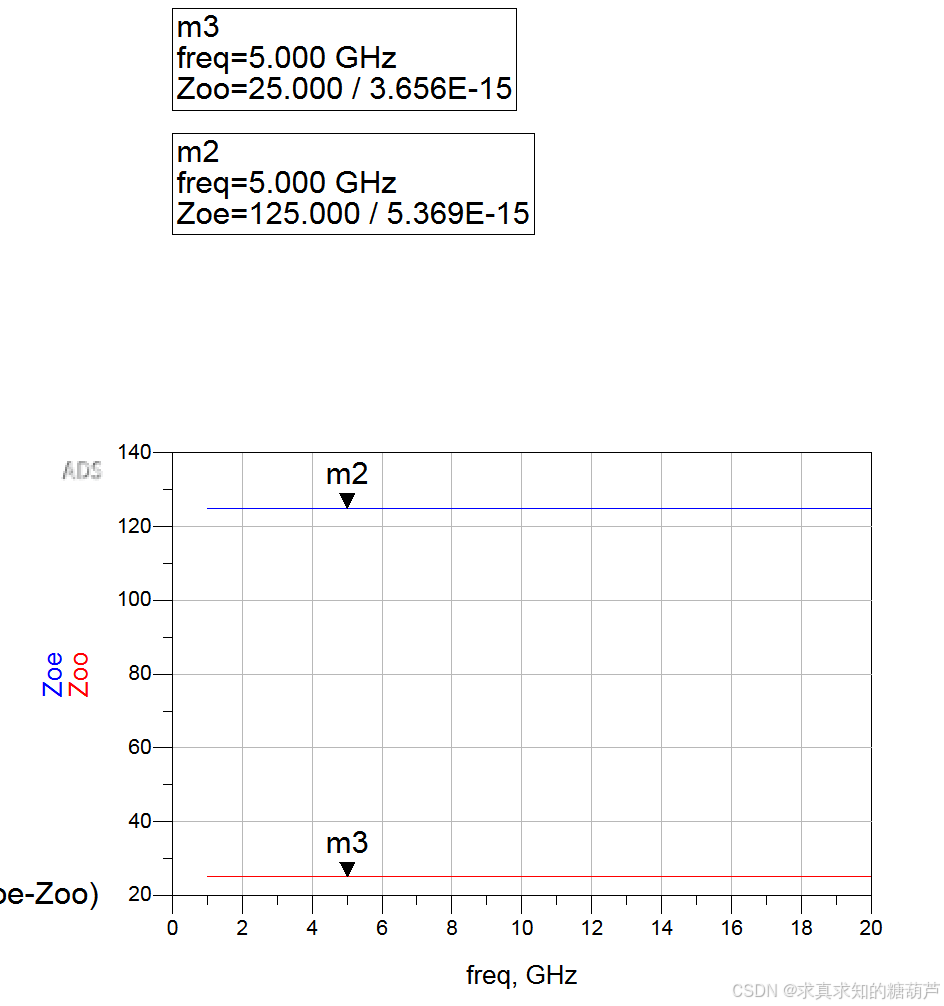
相位与设定一致
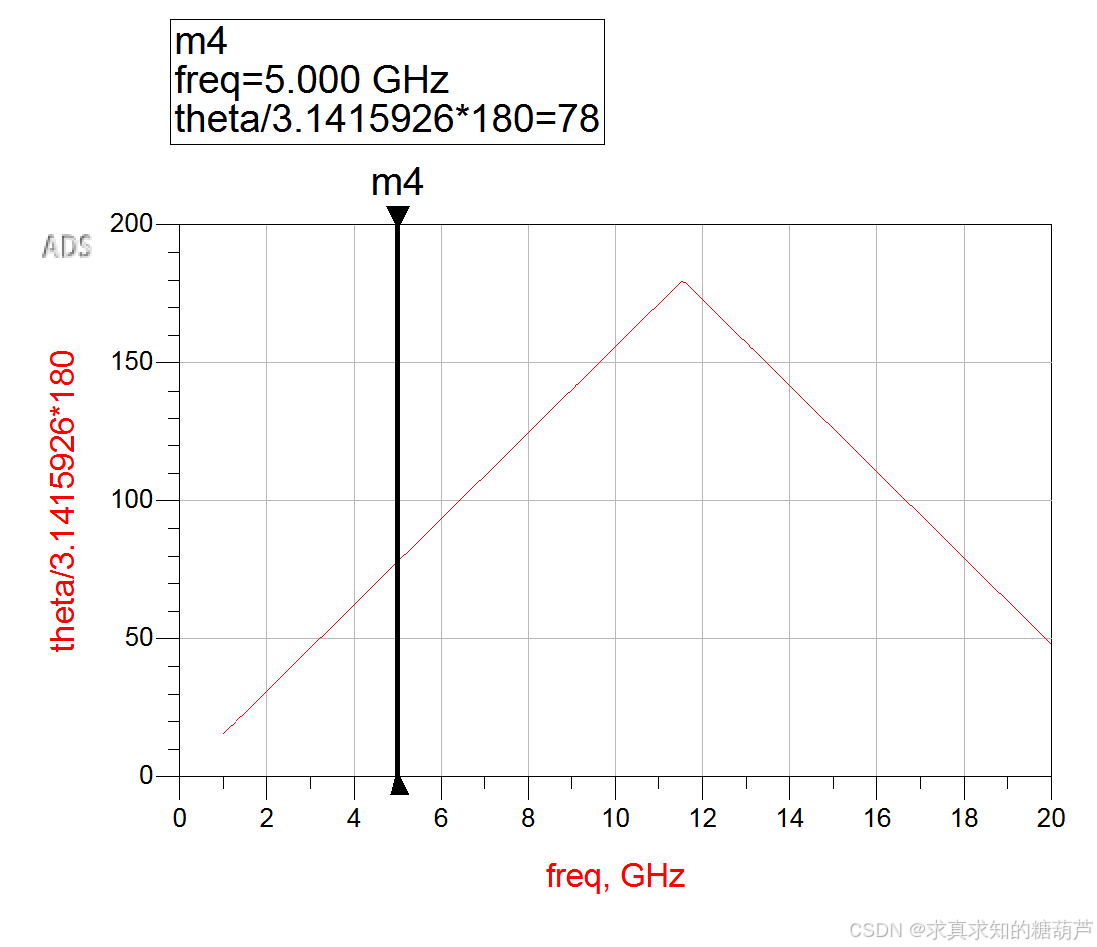
交叉验证一致
如果是不均匀的微带耦合线Z参数矩阵又会变成怎样呢?请听下回分解