[SimpleITK] 教程 63：配准初始化 (Registration Initialization) —— 从几何对齐到手动干预。

博主注： 本文基于 SimpleITK 官方教程 63_Registration_Initialization.ipynb 代码实战整理。重点解析了当自动配准失效时，如何通过几何中心、穷举搜索以及手动标记点来正确初始化配准。

前言：为什么"第一步"至关重要？

在医学图像配准中，初始化（Initialization）直接决定了算法的成败。因为大多数配准算法（如梯度下降）都是迭代优化的，它们非常依赖于"起始位置"。

如果起点离终点太远：算法可能会陷入局部极值（Local Minima），导致配准完全错误。
如果起点足够好：算法能迅速收敛，计算快且准。

本文将按照 自动化程度从高到低 的顺序，介绍三种核心初始化策略。

一、策略一：几何中心对齐 (Centered Transform)

这是最基础的策略。当两张图像的解剖结构方向基本一致（比如都是头朝上），只是空间位置有偏差时，我们可以假设：将两张图像的中心重合，就是最好的起点。

SimpleITK 提供了 CenteredTransformInitializer 来实现这一步，它不需要任何手动干预。

Python

复制代码

initial_transform = sitk.CenteredTransformInitializer(
    fixed_image,
    moving_image,
    sitk.Euler3DTransform(),
    sitk.CenteredTransformInitializerFilter.GEOMETRY, 
)

GEOMETRY: 简单的几何中心对齐（物理坐标系的中心）。
MOMENTS: 基于图像灰度重心（Center of Mass）对齐。

二、策略二：参数空间采样与穷举 (Sampling Parameter Space)

当图像存在较大的旋转差异（例如病人躺反了 180 度），简单的中心对齐就会失效。此时，我们需要在参数空间内进行搜索。

1. 穷举优化器 (Exhaustive Optimizer)

这是一个"笨拙但有效"的方法。它会在参数空间内画一个网格，挨个测试每个位置的相似度分数。

关键参数设置：

Python

复制代码

# 设定网格搜索步数：[角度X, 角度Y, 角度Z, 位移X, 位移Y, 位移Z]
# 这里表示只在 Y 和 Z 轴旋转方向上各搜索一步（0, -step, +step）
registration_method.SetOptimizerAsExhaustive(
    numberOfSteps=[0, 1, 1, 0, 0, 0], 
    stepLength=np.pi 
)

2. 进阶：探索与利用 (Exploration & Exploitation)

穷举优化器的默认行为是只返回"第一名"。但在复杂场景下，我们可能想知道前几名（Top-K）的情况，或者探索不连续的区域。

这时，我们可以利用 观察者模式 (Observer Pattern) 记录穷举过程中的每一步。

代码实现逻辑：

定义"记账员" (Observer)：

创建一个回调函数，每当优化器计算一步，就把当前的 (分数, 参数) 记录到全局列表中。
Python

复制代码

def iteration_observer(registration_method):
    metricvalue_parameters_list.append(
        (registration_method.GetMetricValue(),
         registration_method.GetOptimizerPosition())
    )

绑定事件：

利用 AddCommand 将观察者绑定到 sitkIterationEvent。
Python

复制代码

registration_method.AddCommand(
    sitk.sitkIterationEvent, 
    lambda: iteration_observer(registration_method)
)

筛选 (Exploitation)：

机器跑完后，我们对 metricvalue_parameters_list 进行排序，取出分数最低（最好）的前 K 个参数，分别作为起点进行精细配准。

三、策略三：手动初始化 (Manual Initialization)

当所有自动算法（包括穷举）都无法找到正确的方向时，我们必须引入人工干预（Human in the loop）。这是最后的手段，但几乎总是有效的。

1. 核心思想

我们在固定图像和移动图像上分别手动点击几对解剖对应点 (Landmarks)，然后让计算机算出一个能让这些点尽可能重合的初始变换。

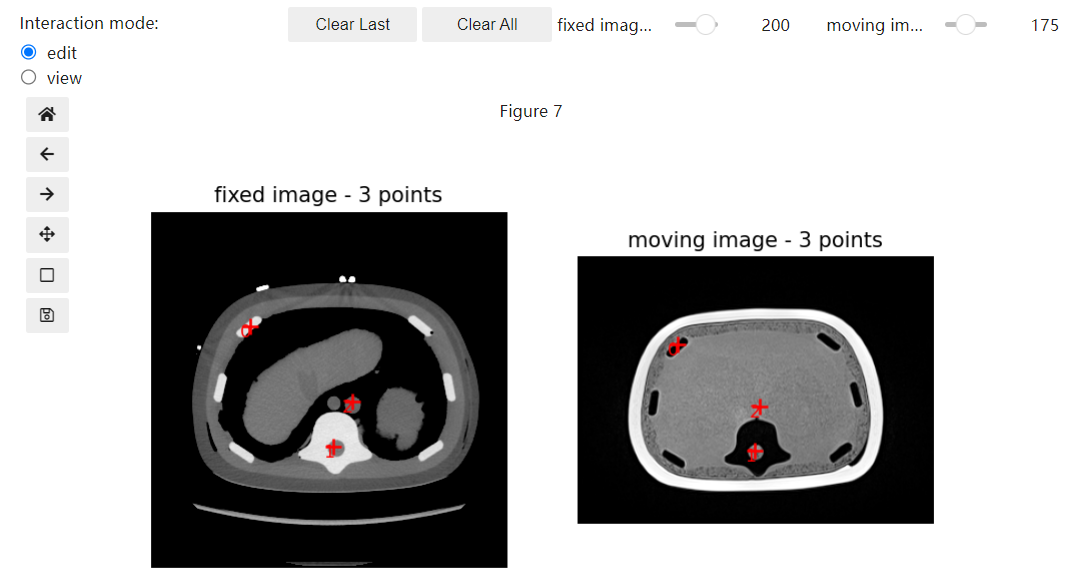
2. 代码深度解析

这一部分涉及到底层数据处理和变换类型的转换，细节很多。

第一步：数据扁平化 (Flattening)

从 GUI 或列表中获取的点通常是元组列表 [(x1,y1,z1), (x2,y2,z2)]。但底层 C++ 算法需要一维数组。

Python

复制代码

# 使用双重列表推导式将数据拉平
# 效果：[(1,2,3), (4,5,6)] -> [1, 2, 3, 4, 5, 6]
fixed_image_points_flat = [c for p in fixed_image_points for c in p]
moving_image_points_flat = [c for p in moving_image_points for c in p]

第二步：计算刚体变换 (SVD算法)

使用 LandmarkBasedTransformInitializer，它通过奇异值分解（SVD）直接算出最优的旋转和平移。注意这里通常先使用 VersorRigid3DTransform（四元数），因为它在数学上更严谨。

Python

复制代码

init_transform = sitk.VersorRigid3DTransform(
    sitk.LandmarkBasedTransformInitializer(
        sitk.VersorRigid3DTransform(), 
        fixed_image_points_flat, 
        moving_image_points_flat
    )
)

第三步：类型转换 (Versor -> Euler)

这是一个容易被忽视的高级技巧。

为什么要转？ Versor（四元数）要求参数模长为1，在后续的优化过程中容易因数值误差导致不稳定。Euler（欧拉角）没有约束，对优化器更友好。
怎么转？ 必须显式拷贝 中心 (Center)、矩阵和位移。

Python

复制代码

initial_transform = sitk.Euler3DTransform()
# 关键点：必须同步旋转中心！否则图像会绕原点旋转而飞出视野
initial_transform.SetCenter(init_transform.GetCenter()) 
initial_transform.SetMatrix(init_transform.GetMatrix())
initial_transform.SetTranslation(init_transform.GetTranslation())

总结

在 SimpleITK 63_Registration_Initialization 教程中，我们学到了：

先尝试自动对齐 ：使用 CenteredTransformInitializer。
大角度旋转用穷举 ：配合 ExhaustiveOptimizer 和观察者模式来寻找全局最优的初始点。
最后手段用手动 ：通过 LandmarkBasedTransformInitializer 利用人工标记点，注意数据扁平化和变换类型的转换细节。

掌握了这些初始化技巧，才能让后续的 ImageRegistrationMethod 跑得稳、准、快。

[SimpleITK] 教程 63：配准初始化 (Registration Initialization) —— 从几何对齐到手动干预。

前言：为什么"第一步"至关重要？

一、 策略一：几何中心对齐 (Centered Transform)

二、 策略二：参数空间采样与穷举 (Sampling Parameter Space)

1. 穷举优化器 (Exhaustive Optimizer)

2. 进阶：探索与利用 (Exploration & Exploitation)

三、 策略三：手动初始化 (Manual Initialization)

1. 核心思想

2. 代码深度解析

第一步：数据扁平化 (Flattening)

第二步：计算刚体变换 (SVD算法)

第三步：类型转换 (Versor -> Euler)

总结

一、策略一：几何中心对齐 (Centered Transform)

二、策略二：参数空间采样与穷举 (Sampling Parameter Space)

三、策略三：手动初始化 (Manual Initialization)