1. 核心关系与贝叶斯定理
贝叶斯定理是三者的桥梁:
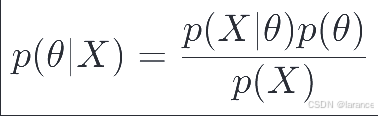
其中:
-
\\theta:未知参数(或假设)
-
X:观测数据
-
p(\\theta):先验概率
-
p(X\|\\theta):似然概率
-
p(\\theta\|X):后验概率
-
p(X):边际似然(证据)
直观公式:后验 \\propto 似然 \\times 先验
2. 先验概率(Prior Probability)
定义
在观察到任何数据之前,基于已有知识对参数 \\theta 的主观概率分布。
关键特性
-
主观性:反映分析者的初始信念,可能基于历史数据、理论或经验。
-
形式:可以是信息性先验(如"硬币大概率是公平的")或无信息先验(如均匀分布,表示"一无所知")。
-
作用:当数据稀缺时,先验对后验影响较大;数据丰富时,其影响减弱。
示例
-
抛硬币前,我们认为正面概率 \\theta 很可能在0.5附近:\\theta \\sim \\text{Beta}(10,10)。
-
若毫无先验信息,可用无信息先验:\\theta \\sim \\text{Uniform}(0,1)。
3. 似然概率(Likelihood)
定义
给定参数 \\theta 时,观测到当前数据 X 的可能性。它是 \\theta 的函数,不是概率分布(因为对 \\theta 的积分不一定为1)。
关键特性
-
数据驱动:完全由观测数据决定,是样本信息的数学表达。
-
频率学派核心:频率学派用似然函数进行推断(如最大似然估计),但不使用先验。
-
注意 :似然函数值的大小只有相对意义,比较不同 \\theta 下的似然值才有意义。
示例
抛硬币10次得7次正面,似然函数为:
L(θ)=p(X∣θ)=θ7(1−θ)3L(θ)=p(X∣θ)=θ7(1−θ)3
4. 后验概率(Posterior Probability)
定义
结合先验信息与观测数据后,参数 \\theta 的更新概率分布。
关键特性
-
贝叶斯推断的核心:所有统计推断(点估计、区间估计、假设检验)都基于后验分布。
-
平衡先验与数据:后验是先验与似然的折衷。数据越多,似然的影响越强。
-
计算难点:分母 p(X) = \\int p(X\|\\theta)p(\\theta)d\\theta 常涉及高维积分,需用MCMC等数值方法近似。
示例
在先验 \\theta \\sim \\text{Beta}(2,2)、观测到7正3反后:
p(θ∣X)∝θ7(1−θ)3⋅θ1(1−θ)1=θ8(1−θ)4p(θ∣X)∝θ7(1−θ)3⋅θ1(1−θ)1=θ8(1−θ)4
即后验分布为 \\text{Beta}(9,5)。
5. 三者的动态关系可视化
假设我们观察抛硬币实验,先验设为 \\text{Beta}(2,2):
| 观察数据(正/反) | 先验分布 | 后验分布 | 说明 |
|---|---|---|---|
| 0次抛掷 | Beta(2,2) | Beta(2,2) | 无数据,后验=先验 |
| 7正3反 | Beta(2,2) | Beta(9,5) | 后验峰值右移,更接近0.7 |
| 70正30反 | Beta(2,2) | Beta(72,32) | 数据主导,后验尖锐集中在0.68附近 |
图形趋势:
-
先验:初始信念(可能较宽泛)。
-
似然:数据提供的信号(可能峰值与先验不同)。
-
后验:二者结合,通常位于先验与似然峰值之间,且数据量越大越接近似然峰值。
6. 与频率学派估计的对比
| 方面 | 贝叶斯方法 | 频率学派方法 |
|---|---|---|
| 参数性质 | 随机变量,有概率分布 | 固定未知常数 |
| 推断依据 | 后验分布 p(\\theta|X) | 似然函数 L(\\theta)=p(X|\\theta) |
| 区间估计 | 可信区间:\\theta 有95%概率落在此区间 | 置信区间:重复抽样下95%区间包含真值 |
| 先验信息 | 明确使用先验 p(\\theta) | 不使用先验 |
| 点估计 | 后验均值、中位数、众数 | 最大似然估计(MLE) |
频率学派⼝中的概率表示的是事件发⽣频率的极限值,
在频率学派眼中,当重复试验的次数趋近于⽆穷⼤时,事件发⽣的频率会收敛到真实的概率 之上。这种观点背后暗含了⼀个前提,那就是概率是⼀个确定的值,并不会受单次观察结果 的影响。
频 率统计理论的核⼼在于认定待估计的参数是固定不变的常量,讨论参数的概率分布是没有意 义的;⽽⽤来估计参数的数据是随机的变量,每个数据都是参数⽀配下⼀次独⽴重复试验的 结果。由于参数本身是确定的,那频率的波动就并⾮来源于参数本身的不确定性,⽽是由有 限次观察造成的⼲扰⽽导致
频率学派认为概率是随机事件发⽣频率的极限值; 频率学派执⾏参数估计时,视参数为确定取值,视数据为随机变量; 频率学派主要使⽤最⼤似然估计法,让数据在给定参数下的似然概率最⼤化; 频率学派对应机器学习中的统计学习,以经验⻛险最⼩化作为模型选择的准则。
为了解决频率主义的问题,⻉叶斯学派给出了⼀种更加通⽤的概率定义:概率表示的是客观 上事件的可信程度(degree of belief),也可以说成是主观上主体对事件的信任程度,它 是建⽴在对事件的已有知识基础上的。
⻉叶斯学派认为概率是事件的可信程度或主体对事件的信任程度; ⻉叶斯学派执⾏参数估计时,视参数为随机变量,视数据为确定取值; ⻉叶斯学派主要使⽤最⼤后验概率法,让参数在先验信息和给定数据下的后验概率最⼤ 化; ⻉叶斯学派对应机器学习中的概率图模型,可以在模型预测和选择中提供更加完整的信 息