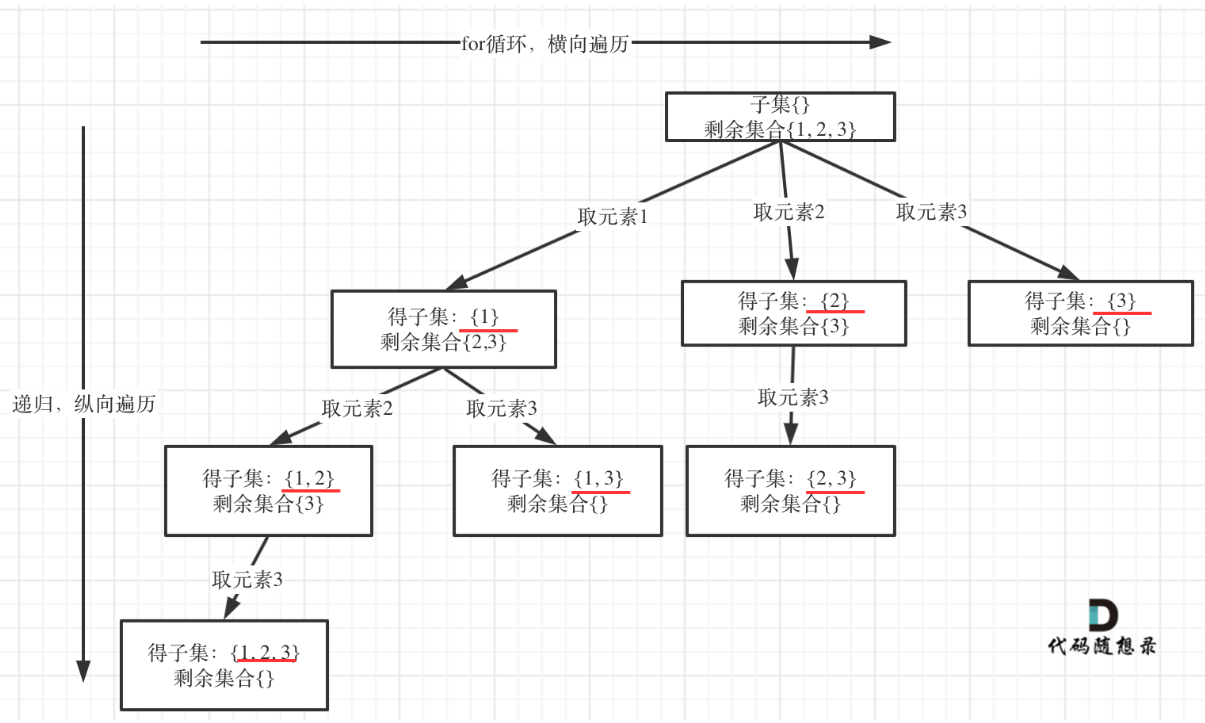
剩余集合为空的时候,就是叶子节点。
那么什么时候剩余集合为空呢?
就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了,代码如下:
cpp
if (startIndex >= nums.size()) {
return;
}
cpp
class Solution {
private:
vector<vector<int>> result; // 存储所有子集结果
vector<int> path; // 存储当前路径(当前正在构建的子集)
// 回溯函数
void backtracking(vector<int>& nums, int startIndex) {
// 1. 收集当前路径(子集)
// 注意:这里放在递归开头,可以确保空集和所有中间子集都被收集
result.push_back(path);
// 2. 递归终止条件(实际上可以省略,因为for循环会自然结束)
// 当startIndex超过数组边界时返回
if (startIndex >= nums.size()) {
return;
}
// 3. 横向遍历:从startIndex开始选择元素
for (int i = startIndex; i < nums.size(); i++) {
// 3.1 选择当前元素(做决策)
path.push_back(nums[i]);
// 3.2 纵向递归:从下一个位置继续选择(避免重复)
// i+1 保证每个元素只使用一次,生成组合而不是排列
backtracking(nums, i + 1);
// 3.3 撤销选择(回溯到上一步)
path.pop_back();
}
// 递归结束返回后,继续for循环选择下一个元素
}
public:
// 主函数:生成所有子集
vector<vector<int>> subsets(vector<int>& nums) {
// 清空结果集和路径(避免多次调用时数据残留)
result.clear();
path.clear();
// 从索引0开始回溯
backtracking(nums, 0);
// 返回所有子集
return result;
}
};为什么不能把 result.push_back(path) 放在 if 语句
cpp
if (startIndex >= nums.size()) {
result.push_back(path); // 只在终止条件收集
return;
}用 nums = [1,2,3] 测试错误方案:
1. backtracking(nums, 0) startIndex=0,不进if for循环 i=0:选1 2. backtracking(nums, 1) startIndex=1,不进if for循环 i=1:选2 3. backtracking(nums, 2) startIndex=2,不进if for循环 i=2:选3 4. backtracking(nums, 3) startIndex=3 >= 3,进if result.push_back([1,2,3]) // 只收集了这个! 返回
最终结果 result = [ [1,2,3] // 只有一个子集! ]
为什么这样会漏掉子集
-
只收集叶子节点:
-
错误方案只在递归到底(
startIndex >= nums.size())时才收集 -
这意味着只收集完整的子集(如
[1,2,3]) -
漏掉了所有中间状态 (如
[1],[1,2],[2]等)
-
初始状态
result = [] ,path = [] 调用backtracking(nums,0)
第1层递归 :调用backtracking(nums,0)
1. result.push_back([]) // 因为此时path = [],所以相当于收集空集 result = [[]] 2. for循环 i=0(i从0到2) i=0: path.push_back(1) // path = [1] 调用backtracking(nums,1)
第2层递归:backtracking(nums, 1)
1. result.push_back([1]) // 收集子集[1] result = [[], [1]] 2. for循环 i=1 (i从1到2) i=1: path.push_back(2) // path = [1,2] 调用backtracking(nums,2)
第3层递归:backtracking(nums, 2)
1. result.push_back([1,2]) // 收集子集[1,2] result = [[], [1], [1,2]] 2. for循环 i=2 (i从2到2) i=2: path.push_back(3) // path = [1,2,3] 调用backtracking(nums,3)
第4层递归:backtracking(nums, 3)
1. result.push_back([1,2,3]) // 收集子集[1,2,3] result = [[], [1], [1,2], [1,2,3]] 2. startIndex=3 >= nums.size()=3,直接返回
回到第3层递归
path.pop_back() // 之前的path = [1,2,3],现在移除3,path = [1,2] for循环彻底结束(i=2是最后一个) 返回第2层递归
回到第2层递归
path.pop_back() // 之前path = [1,2],现在移除2,现在path = [1] i++,for循环继续 i=2 i=2: path.push_back(3) // path = [1,3] 调用backtracking(nums,3)
第3层递归:backtracking(nums, 3)(新分支)
1. result.push_back([1,3]) // 收集子集[1,3] result = [[], [1], [1,2], [1,2,3], [1,3]] 2. startIndex=3 >= 3,直接返回
回到第2层递归
path.pop_back() // 之前的path = [1,3],移除3,path = [1] i++ //i从2变成3,不满足for循环条件,所以for循环结束
回到第1层递归
执行回溯操作(之前i=0 ,path = [1]) path.pop_back() // 移除1,现在path = [] i++ ,for循环继续 i=1 i=1: path.push_back(2) // path = [2] 调用backtracking(nums,2)
第2层递归:backtracking(nums, 2)(新分支)
1. result.push_back([2]) // 收集子集[2] result = [[], [1], [1,2], [1,2,3], [1,3], [2]] 2. for循环 i=2 (i从2到2) i=2: path.push_back(3) // path = [2,3]
.......
.......
.......