本文参考Huei Wang老师课题组的文献K. -J. Koh and G. M. Rebeiz, "0.13-μ\muμm CMOS Phase Shifters for X-, Ku-, and K-Band Phased Arrays," P. -H. Tsai, Y. -H. Lin, J. -L. Kuo, Z. -M. Tsai and H. Wang, "Broadband Balanced Frequency Doublers With Fundamental Rejection Enhancement Using a Novel Compensated Marchand Balun," in IEEE Transactions on Microwave Theory and Techniques, vol. 61, no. 5, pp. 1913-1923, May 2013, doi: 10.1109/TMTT.2013.2255618.从中摘录marchand巴伦段,稍微增加一些推导过程,并且指出其中公式的推导笔误 用红笔标出,仅供学习使用
摘要--- 本文提出了一种新颖的补偿技术,用于改善因耦合线的奇模与偶模相速度不等而导致的传输线巴伦不平衡问题。利用这种方法,可以有效地增强采用传输线巴伦的平衡倍频器的基波抑制能力。为了验证这一概念,在CMOS工艺中设计、制造并测量了两个使用改进型传输线巴伦的单平衡倍频器。一个工作在15-36 GHz的倍频器具有-10 dB的转换增益,82.4%的3 dB带宽和33 dB的基波抑制。另一个工作在95-150 GHz的倍频器实现了-7.9 dB的转换增益,45%的3 dB带宽和30 dB的基波抑制。所提出的补偿技术使这些倍频器具有宽带宽和高基波抑制的特点。
关键词---宽带,CMOS,频率倍频器,基波抑制,传输线巴伦。
I. 引言
近年来,无线通信的工作频率不断提高,以获得更多带宽来适应高数据速率。在高频下设计具有宽调谐范围、良好相位噪声和平坦输出功率的压控振荡器变得困难。因此,通常利用宽带频率倍频器与低频振荡器级联来实现高频源。
实现宽带倍频器有多种拓扑结构。分布式结构被广泛用于实现宽带性能[1],其基波信号通过高通漏极线和滤波器被抑制[2]。当基波信号和二次谐波信号的频率范围重叠时,分布式倍频器难以获得足够的基波抑制[2]。平衡结构用于抑制倍频器中重叠的基波信号[3]-[5]。基于共栅/共源场效应晶体管(FET)平衡配置,基波信号在输出端口反相。然而,这种方法的工作频率受到共源FET反相特性的限制[3]。双平衡二极管倍频器的开发实现了高工作频率和优异的基波抑制[4],但该二极管倍频器需要高输入功率来驱动二极管进入非线性区域。采用单平衡配置的有源FET倍频器克服了上述缺点,例如对高输入功率的要求以及基波和二次谐波频带的重叠[5]。在单平衡倍频器的设计中,传输线巴伦通常因其宽带性能而被使用[5]。传输线巴伦可以在单片微波集成电路(MMIC)中使用两个耦合线节实现 ,例如多层耦合结构[6]、边缘耦合线[7]、兰格耦合器[8]或螺旋形耦合线[9] 。这些耦合线的奇模和偶模相速度不相等 。使用这些耦合线,传输线巴伦无法完美地将不平衡信号转换为平衡信号。由于传输线巴伦的不平衡,平衡倍频器的基波信号无法在输出端口被完美消除。对于平衡倍频器而言,在宽带宽上实现高基波抑制是一个挑战。
本文提出了一种改善传输线巴伦平衡的补偿技术 。它可以减少由于耦合线奇模和偶模相速度不等而导致的传输线巴伦不平衡。介绍了两个采用此方法增强基波抑制的单平衡倍频器。这些倍频器的输出频率分别为15-36 GHz和95-150 GHz。这些倍频器的基波抑制优于30 dB。两个倍频器都具有宽带宽和高基波抑制的特点。
II. 补偿型传输线巴伦的概念
A. 补偿型传输线巴伦的分析
我们提出了一种方法来减少由于耦合线奇偶模相速度不等而导致的传输线巴伦的不完美平衡性能。所提出的补偿型传输线巴伦的示意图如图1所示。
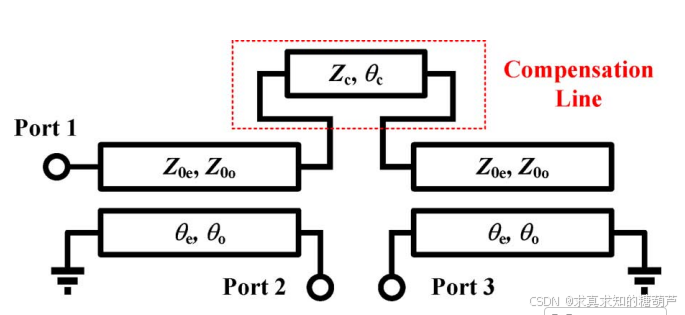
图1. 所提补偿型Marchand平衡器电路示意图。
θe\theta_{e}θe 和 θo\theta_{o}θo 是耦合线的偶模和奇模电气长度 。Z0eZ_{0e}Z0e 和 Z0oZ_{0o}Z0o 是耦合线的偶模和奇模特性阻抗 。θc\theta_{c}θc 和 ZcZ_{c}Zc 是补偿线的电气长度和特性阻抗。这个巴伦基于传统的传输线巴伦,由两个耦合线节和一段传输线组成。所提出的传输线巴伦与传统传输线巴伦的区别在于额外的补偿线。通过使用这条补偿线,可以改善传输线巴伦的平衡性能。为了分析这种补偿机制,采用了使用广义对称四端口网络推导三端口巴伦的技术[10]。
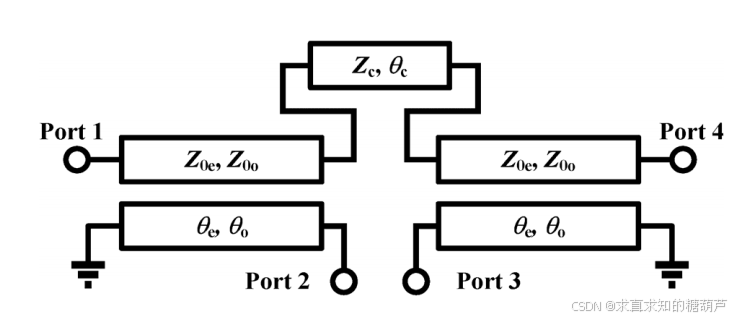
图2. 对称四端口电路示意图(用于偶模与奇模分析)。
图2显示了对称四端口网络,其偶模和奇模半电路如图3所示。这个四端口网络与补偿型传输线巴伦类似,只是端口数量不同。 补偿型传输线巴伦的S矩阵可推导为 (1),如下所示,
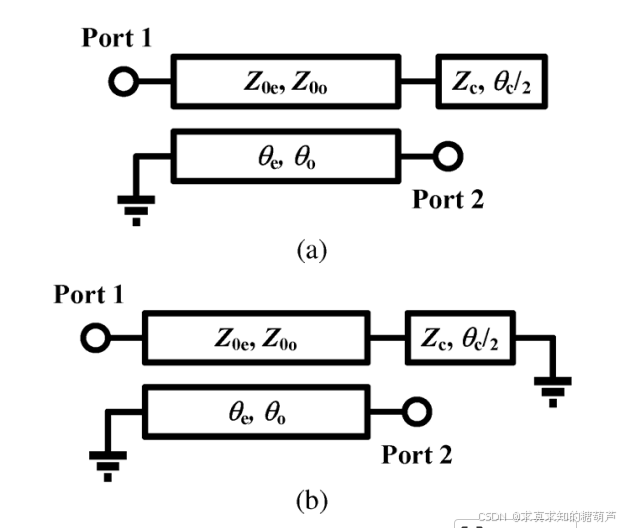
图3. 图2(a)所示网络的半电路:(a)偶模;(b)奇模。
S\](blaun)=\[S11(4port)+S14(4port)21−S11(4port)S12(4port)+S13(4port)S14(4port)1−S11(4port)S13(4port)+S12(4port)S14(4port)1−S11(4port)S12(4port)+S13(4port)S14(4port)1−S11(4port)S22(4port)+S13(4port)21−S11(4port)S23(4port)+S12(4port)S13(4port)1−S11(4port)S13(4port)+S14(4port)S12(4port)1−S11(4port)S23(4port)+S12(4port)S13(4port)1−S11(4port)S22(4port)+S12(4port)21−S11(4port)\](1) \\begin{array}{r}{\[S\]_{(\\text{blaun})}=\\left\[\\begin{array}{cccc}{S_{11_{(4port)}}+\\frac{S_{14_{(4port)}}\^{2}}{1-S_{11_{(4port)}}}}\&{S_{12_{(4port)}}+\\frac{S_{13_{(4port)}}S_{14_{(4port)}}}{1-S_{11_{(4port)}}}}\&{S_{13_{(4port)}}+\\frac{S_{12_{(4port)}}S_{14_{(4port)}}}{1-S_{11_{(4port)}}}}\\\\{S_{12_{(4port)}}+\\frac{S_{13_{(4port)}}S_{14_{(4port)}}}{1-S_{11_{(4port)}}}}\&{S_{22_{(4port)}}+\\frac{S_{13_{(4port)}}\^{2}}{1-S_{11_{(4port)}}}}\&{S_{23_{(4port)}}+\\frac{S_{12_{(4port)}}S_{13_{(4port)}}}{1-S_{11_{(4port)}}}}\\\\{S_{13_{(4port)}}+\\frac{S_{14_{(4port)}}S_{12_{(4port)}}}{1-S_{11_{(4port)}}}}\&{S_{23_{(4port)}}+\\frac{S_{12_{(4port)}}S_{13_{(4port)}}}{1-S_{11_{(4port)}}}}\&{S_{22_{(4port)}}+\\frac{S_{12_{(4port)}}\^{2}}{1-S_{11_{(4port)}}}}\\end{array}\\right\](1) } \\end{array} \[S\](blaun)= S11(4port)+1−S11(4port)S14(4port)2S12(4port)+1−S11(4port)S13(4port)S14(4port)S13(4port)+1−S11(4port)S14(4port)S12(4port)S12(4port)+1−S11(4port)S13(4port)S14(4port)S22(4port)+1−S11(4port)S13(4port)2S23(4port)+1−S11(4port)S12(4port)S13(4port)S13(4port)+1−S11(4port)S12(4port)S14(4port)S23(4port)+1−S11(4port)S12(4port)S13(4port)S22(4port)+1−S11(4port)S12(4port)2 (1) 其中 S11(4−port)S_{11(4-port)}S11(4−port), S12(4−port)S_{12(4-port)}S12(4−port), S13(4−port)S_{13(4-port)}S13(4−port), S14(4−port)S_{14(4-port)}S14(4−port), S22(4−port)S_{22(4-port)}S22(4−port), 和 S23(4−port)S_{23(4-port)}S23(4−port) 是图2中四端口网络的S参数。方程 S21(blaun)=−S31(blaun)S_{21( blaun)}=-S_{31( blaun)}S21(blaun)=−S31(blaun) 被定义为平衡条件。这个条件是 S214−porte=0(2) S_{21_{4-port}}\^{e}=0\\qquad(2) S214−porte=0(2) 其中 S21(4−port)eS_{21(4-port)}\^{e}S21(4−port)e 是四端口网络偶模的S参数,类似于\[10\]中的定义。**至于为什么要求(2)式条件详细推导见附录**。为了实现完美的幅度和相位平衡,功率不能在偶模电路中从端口1传输到端口2。参考图3(a),偶模电路的Y参数推导为(3),如下所示,(Y214 porteY_{21_{4\\text{ port}}}\^{e}Y214 porte可以视为奇偶模相速度不等引起的**不平衡项**。) *** ** * ** *** 我是分割线 **论文里给的Y214 porteY_{21_{4\\text{ port}}}\^{e}Y214 porte有误(作者笔误)** Y214 porte=jY0eY0o(cscθocotθe−cscθe−cotθo)−Yctanθc2(Y0ocscθo−Y0ecscθe)2Yctanθc2(Y0ocotθo+Y0ecotθe)(3) Y_{21_{4\\text{ port}}}\^{e}=j\\frac{Y_{0e}Y_{0o}(\\csc\\theta_{o}\\cot\\theta_{e}-\\csc\\theta_{e}-\\cot\\theta_{o})-Y_{c}\\tan\\frac{\\theta_{c}}{2}(Y_{0o}\\csc\\theta_{o}-Y_{0e}\\csc\\theta_{e})}{2Y_{c}\\tan\\frac{\\theta_{c}}{2}(Y_{0o}\\cot\\theta_{o}+Y_{0e}\\cot\\theta_{e})}(3) Y214 porte=j2Yctan2θc(Y0ocotθo+Y0ecotθe)Y0eY0o(cscθocotθe−cscθe−cotθo)−Yctan2θc(Y0ocscθo−Y0ecscθe)(3) (3)公式推导如下  参考**耦合传输线分析学习笔记(七)不对称耦合微带线Y参数矩阵推导与应用**对于上图所示的耦合线**当端口2接地、端口3接特征阻抗为ZcZ_cZc、电长度为θc/2\\theta_c/2θc/2的开路传输线时** ,对称耦合微带线(k=1k=1k=1)的四端口网络可化简为二端口网络(端口1和端口4)。开路传输线的输入导纳为YL=jYctan(θc/2)Y_L = j Y_c \\tan(\\theta_c/2)YL=jYctan(θc/2),其中Yc=1/ZcY_c = 1/Z_cYc=1/Zc。 原四端口Y参数矩阵的元素为: A=Y11=Y22=Y33=Y44=−j2(Y0ecotθe+Y0ocotθo),B=Y12=Y21=Y34=Y43=−j2(Y0ecotθe−Y0ocotθo),C=Y13=Y31=Y24=Y42=j2(Y0ecscθe+Y0ocscθo),D=Y14=Y41=Y23=Y32=j2(Y0ecscθe−Y0ocscθo). \\begin{aligned} A \&= Y_{11} = Y_{22} = Y_{33} = Y_{44} = -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o\\right), \\\\ B \&= Y_{12} = Y_{21} = Y_{34} = Y_{43} = -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e - Y_{0o}\\cot\\theta_o\\right), \\\\ C \&= Y_{13} = Y_{31} = Y_{24} = Y_{42} = \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e + Y_{0o}\\csc\\theta_o\\right), \\\\ D \&= Y_{14} = Y_{41} = Y_{23} = Y_{32} = \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e - Y_{0o}\\csc\\theta_o\\right). \\end{aligned} ABCD=Y11=Y22=Y33=Y44=−2j(Y0ecotθe+Y0ocotθo),=Y12=Y21=Y34=Y43=−2j(Y0ecotθe−Y0ocotθo),=Y13=Y31=Y24=Y42=2j(Y0ecscθe+Y0ocscθo),=Y14=Y41=Y23=Y32=2j(Y0ecscθe−Y0ocscθo). **利用端口条件 U2=0U_2 = 0U2=0和I3=−YLU3I_3 = -Y_L U_3I3=−YLU3,消去U2U_2U2和U3U_3U3,** 考虑对称耦合微带线(k=1k=1k=1)的四端口网络,其Y参数方程为: I1=AU1+BU2+CU3+DU4,I2=BU1+AU2+DU3+CU4,I3=CU1+DU2+AU3+BU4,I4=DU1+CU2+BU3+AU4, \\begin{aligned} I_1 \&= A U_1 + B U_2 + C U_3 + D U_4, \\\\ I_2 \&= B U_1 + A U_2 + D U_3 + C U_4, \\\\ I_3 \&= C U_1 + D U_2 + A U_3 + B U_4, \\\\ I_4 \&= D U_1 + C U_2 + B U_3 + A U_4, \\end{aligned} I1I2I3I4=AU1+BU2+CU3+DU4,=BU1+AU2+DU3+CU4,=CU1+DU2+AU3+BU4,=DU1+CU2+BU3+AU4, 其中 AAA, BBB, CCC, DDD 为对称四端口Y参数矩阵的元素,满足: A=Y11=Y22=Y33=Y44=−j2(Y0ecotθe+Y0ocotθo),B=Y12=Y21=Y34=Y43=−j2(Y0ecotθe−Y0ocotθo),C=Y13=Y31=Y24=Y42=j2(Y0ecscθe+Y0ocscθo),D=Y14=Y41=Y23=Y32=j2(Y0ecscθe−Y0ocscθo). \\begin{aligned} A \&= Y_{11} = Y_{22} = Y_{33} = Y_{44} = -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o\\right), \\\\ B \&= Y_{12} = Y_{21} = Y_{34} = Y_{43} = -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e - Y_{0o}\\cot\\theta_o\\right), \\\\ C \&= Y_{13} = Y_{31} = Y_{24} = Y_{42} = \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e + Y_{0o}\\csc\\theta_o\\right), \\\\ D \&= Y_{14} = Y_{41} = Y_{23} = Y_{32} = \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e - Y_{0o}\\csc\\theta_o\\right). \\end{aligned} ABCD=Y11=Y22=Y33=Y44=−2j(Y0ecotθe+Y0ocotθo),=Y12=Y21=Y34=Y43=−2j(Y0ecotθe−Y0ocotθo),=Y13=Y31=Y24=Y42=2j(Y0ecscθe+Y0ocscθo),=Y14=Y41=Y23=Y32=2j(Y0ecscθe−Y0ocscθo). 端口条件为:端口2接地(U2=0U_2 = 0U2=0),端口3接开路传输线,其输入导纳为 YL=jYctan(θc/2)Y_L = j Y_c \\tan(\\theta_c/2)YL=jYctan(θc/2),且电流满足 I3=−YLU3I_3 = -Y_L U_3I3=−YLU3(电流流出网络)。 **代入 U2=0U_2 = 0U2=0**,简化四端口方程: I1=AU1+CU3+DU4,I2=BU1+DU3+CU4,I3=CU1+AU3+BU4,I4=DU1+BU3+AU4. \\begin{aligned} I_1 \&= A U_1 + C U_3 + D U_4, \\\\ I_2 \&= B U_1 + D U_3 + C U_4, \\\\ I_3 \&= C U_1 + A U_3 + B U_4, \\\\ I_4 \&= D U_1 + B U_3 + A U_4. \\end{aligned} I1I2I3I4=AU1+CU3+DU4,=BU1+DU3+CU4,=CU1+AU3+BU4,=DU1+BU3+AU4. **利用 I3=−YLU3I_3 = -Y_L U_3I3=−YLU3** ,带入第三个方程得到关于 U3U_3U3 的方程: CU1+AU3+BU4=−YLU3. C U_1 + A U_3 + B U_4 = -Y_L U_3. CU1+AU3+BU4=−YLU3. 整理得: (A+YL)U3=−CU1−BU4, (A + Y_L) U_3 = -C U_1 - B U_4, (A+YL)U3=−CU1−BU4, 解得: U3=−CU1+BU4A+YL.(假设 A+YL≠0) U_3 = -\\frac{C U_1 + B U_4}{A + Y_L}. \\quad (\\text{假设 } A + Y_L \\neq 0) U3=−A+YLCU1+BU4.(假设 A+YL=0) **将 U3U_3U3 代入 I1I_1I1 和 I4I_4I4 的表达式** ,消去 U3U_3U3: * 对于 I1I_1I1: I1=AU1+C(−CU1+BU4A+YL)+DU4=AU1−C2U1+BCU4A+YL+DU4=(A−C2A+YL)U1+(D−BCA+YL)U4. \\begin{aligned} I_1 \&= A U_1 + C\\left(-\\frac{C U_1 + B U_4}{A + Y_L}\\right) + D U_4 \\\\ \&= A U_1 - \\frac{C\^2 U_1 + B C U_4}{A + Y_L} + D U_4 \\\\ \&= \\left(A - \\frac{C\^2}{A + Y_L}\\right) U_1 + \\left(D - \\frac{B C}{A + Y_L}\\right) U_4. \\end{aligned} I1=AU1+C(−A+YLCU1+BU4)+DU4=AU1−A+YLC2U1+BCU4+DU4=(A−A+YLC2)U1+(D−A+YLBC)U4. * 对于 I4I_4I4: I4=DU1+B(−CU1+BU4A+YL)+AU4=DU1−BCU1+B2U4A+YL+AU4=(D−BCA+YL)U1+(A−B2A+YL)U4. \\begin{aligned} I_4 \&= D U_1 + B\\left(-\\frac{C U_1 + B U_4}{A + Y_L}\\right) + A U_4 \\\\ \&= D U_1 - \\frac{B C U_1 + B\^2 U_4}{A + Y_L} + A U_4 \\\\ \&= \\left(D - \\frac{B C}{A + Y_L}\\right) U_1 + \\left(A - \\frac{B\^2}{A + Y_L}\\right) U_4. \\end{aligned} I4=DU1+B(−A+YLCU1+BU4)+AU4=DU1−A+YLBCU1+B2U4+AU4=(D−A+YLBC)U1+(A−A+YLB2)U4. **得到二端口Y参数矩阵**: 由上述表达式,可得二端口网络(端口1和端口4)的Y参数矩阵为: \[I1I4\]=\[Y114 port eY124 port eY214 port eY224 port e\]\[U1U4\], \\begin{bmatrix} I_1 \\\\ I_4 \\end{bmatrix} = \\begin{bmatrix} Y_{11_{4\\text{ port }}}\^e \& Y_{12_{4\\text{ port }}}\^{e} \\\\ Y_{21_{4\\text{ port }}}\^{e} \& Y_{22_{4\\text{ port }}}\^e \\end{bmatrix} \\begin{bmatrix} U_1 \\\\ U_4 \\end{bmatrix}, \[I1I4\]=\[Y114 port eY214 port eY124 port eY224 port e\]\[U1U4\], 其中 Y114 port e=A−C2A+YL,Y124 port e=Y214 port e=D−BCA+YL,Y224 port e=A−B2A+YL. \\boxed{ \\begin{aligned} Y_{11_{4\\text{ port }}}\^e \&= A - \\frac{C\^2}{A + Y_L}, \\\\ Y_{12_{4\\text{ port }}}\^{e}\&= Y_{21_{4\\text{ port }}}\^{e} = D - \\frac{BC}{A + Y_L}, \\\\ Y_{22_{4\\text{ port }}}\^e \&= A - \\frac{B\^2}{A + Y_L}. \\end{aligned}} Y114 port eY124 port eY224 port e=A−A+YLC2,=Y214 port e=D−A+YLBC,=A−A+YLB2. A=−j2(Y0ecotθe+Y0ocotθo),B=−j2(Y0ecotθe−Y0ocotθo),C=j2(Y0ecscθe+Y0ocscθo),D=j2(Y0ecscθe−Y0ocscθo),YL=jYctan(θc/2). \\boxed{ \\begin{aligned} A \&= -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o\\right), \\\\ B \&= -\\frac{j}{2}\\left(Y_{0e}\\cot\\theta_e - Y_{0o}\\cot\\theta_o\\right), \\\\ C \&= \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e + Y_{0o}\\csc\\theta_o\\right), \\\\ D \&= \\frac{j}{2}\\left(Y_{0e}\\csc\\theta_e - Y_{0o}\\csc\\theta_o\\right),\\\\ \&Y_L = j Y_c \\tan \\left(\\theta_c/2\\right). \\end{aligned}} ABCD=−2j(Y0ecotθe+Y0ocotθo),=−2j(Y0ecotθe−Y0ocotθo),=2j(Y0ecscθe+Y0ocscθo),=2j(Y0ecscθe−Y0ocscθo),YL=jYctan(θc/2). 代入ABCD表达式并化简,可得**正确表达式应该如下**: Y214 porte=jY0eY0o(cscθocotθe−cscθecotθo)−Yctanθc2(Y0ocscθo−Y0ecscθe)2Yctanθc2−(Y0ocotθo+Y0ecotθe)(3) Y_{21_{4\\text{ port}}}\^{e}=j\\frac{Y_{0e}Y_{0o}(\\csc\\theta_{o}\\cot\\theta_{e}-\\csc\\theta_{e}\\cot\\theta_{o})-Y_{c}\\tan\\frac{\\theta_{c}}{2}(Y_{0o}\\csc\\theta_{o}-Y_{0e}\\csc\\theta_{e})}{2Y_{c}\\tan\\frac{\\theta_{c}}{2}-(Y_{0o}\\cot\\theta_{o}+Y_{0e}\\cot\\theta_{e})}(3) Y214 porte=j2Yctan2θc−(Y0ocotθo+Y0ecotθe)Y0eY0o(cscθocotθe−cscθecotθo)−Yctan2θc(Y0ocscθo−Y0ecscθe)(3) 同理 Y114 port e=−j2(Y0ecotθe+Y0ocotθo)+(Y0ecscθe+Y0ocscθo)24j(Yctan(θc/2)−12(Y0ecotθe+Y0ocotθo)) Y_{11_{4\\text{ port }}}\^e= -\\frac{j}{2}\\left(Y_{0e} \\cot \\theta_e + Y_{0o} \\cot \\theta_o\\right) + \\frac{ \\left( Y_{0e} \\csc \\theta_e + Y_{0o} \\csc \\theta_o \\right)\^2 }{ 4j \\left( Y_c \\tan(\\theta_c /2) - \\frac{1}{2}\\left(Y_{0e} \\cot \\theta_e + Y_{0o} \\cot \\theta_o\\right) \\right) } Y114 port e=−2j(Y0ecotθe+Y0ocotθo)+4j(Yctan(θc/2)−21(Y0ecotθe+Y0ocotθo))(Y0ecscθe+Y0ocscθo)2 通分后 =2(Y0ecotθe+Y0ocotθo)Yctan(θc/2)−(Y0ecotθe+Y0ocotθo)2+(Y0ecscθe+Y0ocscθo)22j(2Yctan(θc/2)−(Y0ecotθe+Y0ocotθo)) = \\frac{ 2(Y_{0e} \\cot \\theta_e + Y_{0o} \\cot \\theta_o) Y_c \\tan(\\theta_c / 2) - (Y_{0e} \\cot \\theta_e + Y_{0o} \\cot \\theta_o)\^2 + (Y_{0e} \\csc \\theta_e + Y_{0o} \\csc \\theta_o)\^2 }{ 2j \\left( 2Y_c \\tan(\\theta_c / 2) - (Y_{0e} \\cot \\theta_e + Y_{0o} \\cot \\theta_o) \\right) } =2j(2Yctan(θc/2)−(Y0ecotθe+Y0ocotθo))2(Y0ecotθe+Y0ocotθo)Yctan(θc/2)−(Y0ecotθe+Y0ocotθo)2+(Y0ecscθe+Y0ocscθo)2 Y224 port e=−jYctanθc2(Y0ecotθe+Y0ocotθo)−2Y0eY0ocotθecotθo2Yctanθc2−(Y0ecotθe+Y0ocotθo) \\begin{aligned} Y_{22_{4\\text{ port }}}\^e \&= -j \\frac{Y_c \\tan\\frac{\\theta_c}{2}(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o) - 2Y_{0e}Y_{0o}\\cot\\theta_e\\cot\\theta_o}{2Y_c \\tan\\frac{\\theta_c}{2} - (Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o)} \\end{aligned} Y224 port e=−j2Yctan2θc−(Y0ecotθe+Y0ocotθo)Yctan2θc(Y0ecotθe+Y0ocotθo)−2Y0eY0ocotθecotθo =j2Y0eY0ocotθecotθo−Yctan(θc2)(Y0ecotθe+Y0ocotθo)2Yctan(θc2)−(Y0ecotθe+Y0ocotθo) = j \\frac{ 2Y_{0e}Y_{0o}\\cot\\theta_e\\cot\\theta_o - Y_c\\tan\\left(\\dfrac{\\theta_c}{2}\\right) \\left(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o\\right) }{ 2Y_c\\tan\\left(\\dfrac{\\theta_c}{2}\\right) - \\left(Y_{0e}\\cot\\theta_e + Y_{0o}\\cot\\theta_o\\right) } =j2Yctan(2θc)−(Y0ecotθe+Y0ocotθo)2Y0eY0ocotθecotθo−Yctan(2θc)(Y0ecotθe+Y0ocotθo) (如果θc/2=π/2\\theta_c/2 = \\pi/2θc/2=π/2导致tan函数无穷),则需另外处理。 我是分割线 *** ** * ** *** 其中Yctan(θc/2)(Y0ocscθo−Y0ecscθe)Y_{c}\\tan(\\theta_{c}/2)(Y_{0o}\\csc\\theta_{o}-Y_{0e}\\csc\\theta_{e})Yctan(θc/2)(Y0ocscθo−Y0ecscθe) 是用于平衡性能的补偿项。可以观察到,Y21(4port)eY_{21(4port)}\^{e}Y21(4port)e 的分子可以通过补偿项变为零,即, Yctanθc2=Y0eY0o(cotθecscθo−cotθocscθe)(Y0ocscθo−Y0ecscθe).(4) Y_{c}\\tan\\frac{\\theta_{c}}{2}=\\frac{Y_{0e}Y_{0o}(\\cot\\theta_{e}\\csc\\theta_{o}-\\cot\\theta_{o}\\csc\\theta_{e})}{(Y_{0o}\\csc\\theta_{o}-Y_{0e}\\csc\\theta_{e})}.\\quad{(4)} Yctan2θc=(Y0ocscθo−Y0ecscθe)Y0eY0o(cotθecscθo−cotθocscθe).(4) 如果满足(4),则达到平衡条件,从而传输线巴伦是平衡的。(4)的右边是耦合线参数 Y0eY_{0e}Y0e, Y0oY_{0o}Y0o, θe\\theta_{e}θe, 和 θo\\theta_{o}θo 的函数,而(4)的左边是补偿线参数 YcY_{c}Yc 和 θc\\theta_{c}θc 的函数。当耦合线的参数确定后,有无限多个补偿线的解满足(4)。例如,当耦合线参数确定为 Z0e=104ΩZ_{0e}=104\\OmegaZ0e=104Ω, Z0o=24ΩZ_{0o}=24\\OmegaZ0o=24Ω, θe=72∘\\theta_{e}=72\^{\\circ}θe=72∘, 和 θo=90∘\\theta_{o}=90\^{\\circ}θo=90∘ 时,(4)的右边是4.1 mS。(4)的左边相对于补偿线电气长度的关系如图4所示。 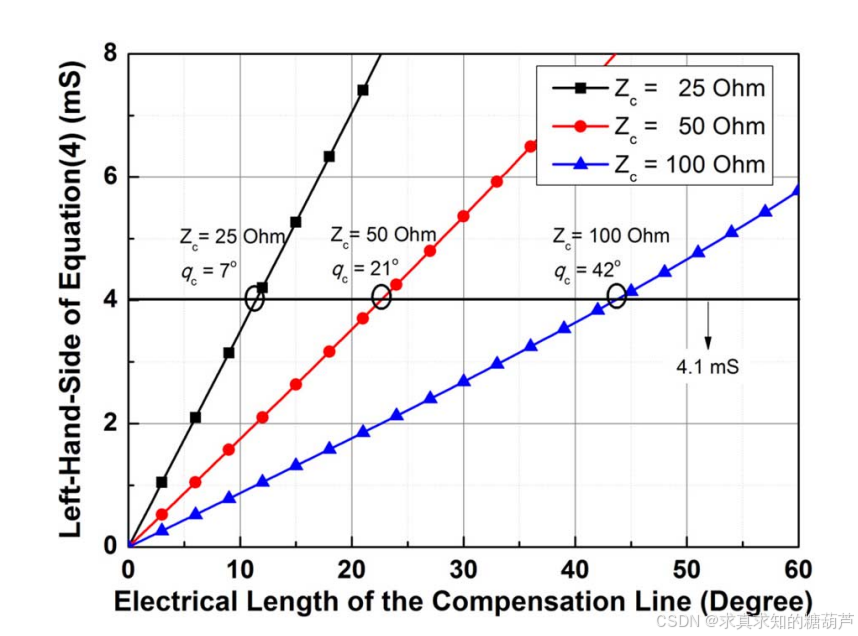 图4. (4)式左侧与补偿线电长度的关系。 对于不同的特性阻抗(25、50和100 Ω),通过补偿线不同的电气长度(7°、21°和42°),(4)的左边可以达到4.1 mS以满足(4)。在这种情况下,当耦合线参数确定(Z0e=104ΩZ_{0e}=104\\OmegaZ0e=104Ω, Z0o=24ΩZ_{0o}=24\\OmegaZ0o=24Ω, θe=90∘\\theta_{e}=90\^{\\circ}θe=90∘, 和 θo=72∘\\theta_{o}=72\^{\\circ}θo=72∘)时,补偿线的 θc\\theta_{c}θc 与 YcY_{c}Yc 的解绘制在图5中。这个图可以帮助设计者选择合适的补偿线解。利用此图,可以轻松获得补偿线的电气长度和特性导纳。 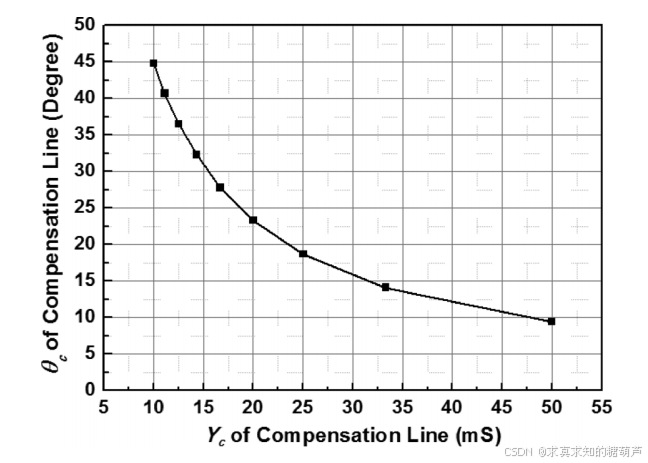 图5. 补偿线路(含耦合线路)的电气长度与特性导纳关系解 #### B. 设计流程与示例 总之,对于补偿型传输线巴伦的设计,建议详细设计流程如下。 1. 对**耦合线进行全波电磁(EM)仿真,并从仿真的耦合线S参数中提取耦合线的 Z0eZ_{0e}Z0e,Z0oZ_{0o}Z0o,θe\\theta_{e}θe 和 θo\\theta_{o}θo。** 2. 使用 **(4)计算并绘制特性导纳与补偿线电气长度之间的关系**。 3. 考虑芯片面积和版图规则,**选择合适的补偿线宽度和长度**。 4. 利用**全波电磁仿真验证完整的补偿型传输线巴伦**的性能。 *** ** * ** *** 一个补偿型Marchand巴伦被设计用于示例设计流程。此巴伦工作于8--18 GHz频段,采用台积电(TSMC)标准体0.18-μ\\boldsymbol{\\mu}μm 1P6M CMOS工艺\[12\],并应用于一个输出频率为15--36 GHz的倍频器。该巴伦的耦合线为宽边耦合线\[13\],由超厚金属(M6)和普通金属(M5)实现。 为了获得高耦合系数,这些耦合线的接地层被挖空以增强偶模特性阻抗\[14\]。图6(a)和(b)展示了耦合线的版图与三维视图。在16 GHz下,耦合线的参数为 Z0e=458ΩZ_{0e}=458\\OmegaZ0e=458Ω, Z0o=33.6ΩZ_{0o}=33.6\\OmegaZ0o=33.6Ω, θe=38.5∘\\theta_{e}=38.5\^{\\circ}θe=38.5∘, 和 θo=66.7∘\\theta_{o}=66.7\^{\\circ}θo=66.7∘。 使用公式(4)计算并绘制了补偿线的特性导纳与其电长度的关系,如图6©所示。考虑到版图布局,选择在16 GHz下 Yc=10.9 mSY_{c}=10.9\\ \\mathrm{mS}Yc=10.9 mS (Zc=92ΩZ_{c}=92\\OmegaZc=92Ω) 且 θc=16.3∘\\theta_{c}=16.3\^{\\circ}θc=16.3∘ 的补偿线来补偿不平衡。补偿线由超厚金属(M6)实现,其物理参数为:宽度3 μm\\mu\\mathrm{m}μm,长度501 μm\\mu\\mathrm{m}μm。 完整的补偿型Marchand巴伦版图及三维视图如图6(f)所示,面积为 180×400 μm2180 \\times 400\\ \\mu\\mathrm{m}\^{2}180×400 μm2。 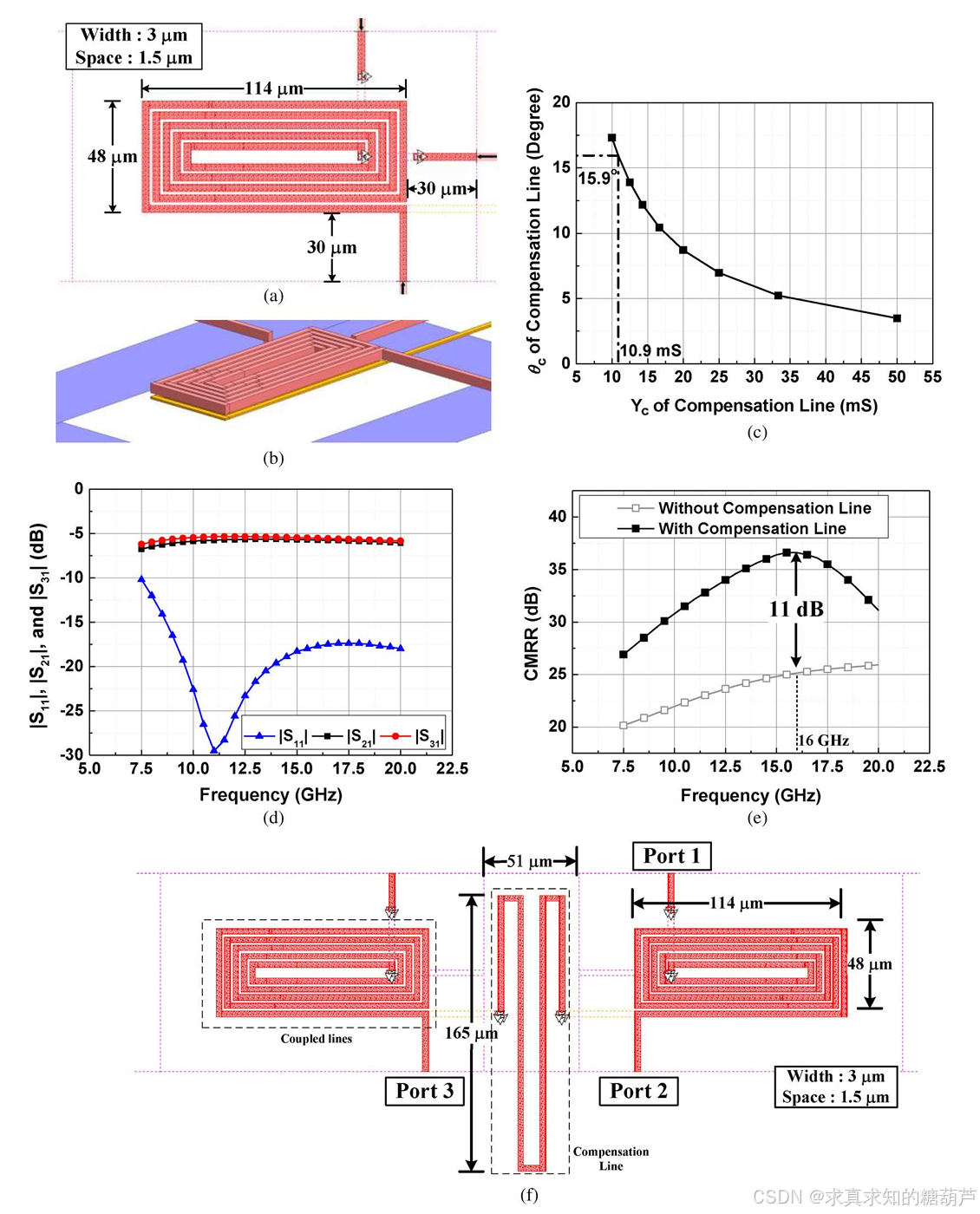 图6. (a) 补偿型Marchand巴伦中耦合线的布局;(b) 三维视图。 (c) 补偿线的特征导纳与电长度的解。 (d) 补偿型Marchand巴伦的仿真S参数。 (e) 带和不带补偿线的Marchand巴伦的仿真共模抑制比(CMRR)。 (f) 补偿型Marchand巴伦的布局。(用于15--36 GHz的倍频器) 使用全波电磁仿真工具(SONNET软件)对该补偿型Marchand巴伦进行了仿真。∣S11∣\|S_{11}\|∣S11∣, ∣S21∣\|S_{21}\|∣S21∣, 和 ∣S31∣\|S_{31}\|∣S31∣ 的结果如图6(d)所示。在8至20 GHz范围内,∣S21∣\|S_{21}\|∣S21∣ 和 ∣S31∣\|S_{31}\|∣S31∣ 优于-7.5 dB,∣S11∣\|S_{11}\|∣S11∣ 优于-10 dB。此外,本文采用了Bockelman和Eisenstadt提出的三端口共模抑制比(CMRR)\[16\]。CMRR的优值(FOM)近似为: CMRR≈(2+Δ)2+θ2(1+Δ)2Δ2+θ2(1+Δ)2≈2+ΔΔ2+θ2(5) \\text{CMRR} \\approx \\sqrt{\\frac{(2+\\Delta)\^{2}+\\theta\^{2}(1+\\Delta)\^{2}}{\\Delta\^{2}+\\theta\^{2}(1+\\Delta)\^{2}}} \\approx \\frac{2+\\Delta}{\\sqrt{\\Delta\^{2}+\\theta\^{2}}}\\quad{(5)} CMRR≈Δ2+θ2(1+Δ)2(2+Δ)2+θ2(1+Δ)2 ≈Δ2+θ2 2+Δ(5) 其中 Δ\\DeltaΔ 和 θ\\thetaθ 是巴伦的幅度和相位不平衡度。如图6(e)所示,在16 GHz下,采用补偿线后Marchand巴伦的CMRR提升了11 dB。 遵循同样的设计流程,在TSMC标准体65-nm 1P9M CMOS工艺\[17\]中实现了用于45--75 GHz频段的补偿型Marchand巴伦。该巴伦用于一个输出频率为95--150 GHz的倍频器。此巴伦的版图和三维视图如图7(a)和(b)所示,面积为 210×36 μm2210 \\times 36\\ \\mu m\^{2}210×36 μm2。在75 GHz下,耦合线的参数为 Z0e=282.9ΩZ_{0e}=282.9\\OmegaZ0e=282.9Ω, Z0o=31.6ΩZ_{0o}=31.6\\OmegaZ0o=31.6Ω, θe=98.9∘\\theta_{e}=98.9\^{\\circ}θe=98.9∘, 和 θo=120∘\\theta_{o}=120\^{\\circ}θo=120∘。  图7. (a) 补偿型Marchand Balun的布局和(b) 三维视图。(c) 补偿型Marchand Balun的模拟 、 和。(d) 带有和不带补偿线的Marchand Balun的模拟CMRR(用于95--150 GHz的倍频器) 在75 GHz下,选择 Zc=74ΩZ_{c}=74\\OmegaZc=74Ω 和 θc=11.6∘\\theta_{c}=11.6\^{\\circ}θc=11.6∘ 来补偿不平衡。该补偿型Marchand巴伦由两个使用超厚金属(M9和M8)的宽边耦合线部分以及一个使用超厚金属(M8)的补偿线组成。如图7(c)(c)(c)所示,在45至75 GHz范围内,∣S21∣\|S_{21}\|∣S21∣ 和 ∣S31∣\|S_{31}\|∣S31∣ 优于-6 dB,∣S11∣\|S_{11}\|∣S11∣ 优于-13 dB。图7(d)展示了有和无补偿线的Marchand巴伦的CMRR。在75 GHz下,采用补偿线后CMRR提高了15 dB。 ### 附录 由公式 (1),我们定义 S21(balun)=−S31(balun)S_{21_{\\text{(balun)}}} = -S_{31_{\\text{(balun)}}}S21(balun)=−S31(balun) 为平衡条件。如果满足此条件,则 Marchand 巴伦完全平衡,即: (S124 port+S134 port)(1+S144 port1−S114 port)=0(A-1) \\left( S_{12_{4\\text{ port}}} + S_{13_{4\\text{ port}}}\\right)\\left(1 + \\frac{S_{14_{4\\text{ port}}}}{1 - S_{11_{4\\text{ port}}}}\\right) = 0 \\quad \\text{(A-1)} (S124 port+S134 port)(1+1−S114 portS144 port)=0(A-1) 这也意味着: 1+S144 port1−S114 port=0(A-2) 1 + \\frac{S_{14_{4\\text{ port}}}}{1 - S_{11_{4\\text{ port}}}} = 0 \\quad \\text{(A-2)} 1+1−S114 portS144 port=0(A-2) 或 S124 port+S134 port=0(A-3) S_{12_{4\\text{ port}}} + S_{13_{4\\text{ port}}} = 0 \\quad \\text{(A-3)} S124 port+S134 port=0(A-3) 可以满足平衡条件;然而,由 (A-2) 可得 S11(4 port)−S14(4 port)=1S_{11_{(4\\text{ port})}} - S_{14_{(4\\text{ port})}} = 1S11(4 port)−S14(4 port)=1,继而: S11(balun)=S114 port+S144 port21−S114 port=S114 port+S144 port2−S144 port=S114 port−S144 port=1(A-4) \\begin{align\*} S_{11_{\\text{(balun)}}} \&= S_{11_{4\\text{ port}}} + \\frac{S_{14_{4\\text{ port}}}\^{2}}{1 - S_{11_{4\\text{ port}}}} \\\\ \&= S_{11_{4\\text{ port}}} + \\frac{S_{14_{4\\text{ port}}}\^{2}}{-S_{14_{4\\text{ port}}}} \\\\ \&= S_{11_{4\\text{ port}}} - S_{14_{4\\text{ port}}} \\\\ \&= 1 \\end{align\*} \\quad \\text{(A-4)} S11(balun)=S114 port+1−S114 portS144 port2=S114 port+−S144 portS144 port2=S114 port−S144 port=1(A-4) 且 S21,31(balun)S_{21,31_{\\text{(balun)}}}S21,31(balun) 为零。这意味着该巴伦无法将非平衡信号转换为平衡信号。(A-2) 的解是平凡解。这意味着该 Marchand 巴伦并非完全平衡。 由 (A-3): S124 port=12(S124 porte+S124 porto)=12(S214 porte+S214 porto)S134 port=12(S124 porte−S124 porto)=12(S214 porte−S214 porto) \\begin{align\*} S_{12_{4\\text{ port}}} \&= \\frac{1}{2}\\left(S_{12_{4\\text{ port}}}\^{e} + S_{12_{4\\text{ port}}}\^{o}\\right) \\\\ \&= \\frac{1}{2}\\left(S_{21_{4\\text{ port}}}\^{e} + S_{21_{4\\text{ port}}}\^{o}\\right) \\\\ S_{13_{4\\text{ port}}} \&= \\frac{1}{2}\\left(S_{12_{4\\text{ port}}}\^{e} - S_{12_{4\\text{ port}}}\^{o}\\right) \\\\ \&= \\frac{1}{2}\\left(S_{21_{4\\text{ port}}}\^{e} - S_{21_{4\\text{ port}}}\^{o}\\right) \\end{align\*} S124 portS134 port=21(S124 porte+S124 porto)=21(S214 porte+S214 porto)=21(S124 porte−S124 porto)=21(S214 porte−S214 porto) 从而得出: S214 porte=0(A-5) S_{21_{4\\text{ port}}}\^{e} = 0 \\quad \\text{(A-5)} S214 porte=0(A-5)