【仿真到实战】STM32落地EKF算法实现锂电池SOC高精度估算(含硬件驱动与源码)

对于做电池管理(BMS)算法研究的同学来说，在Matlab/Simulink里跑通二阶RC模型和扩展卡尔曼滤波(EKF)通常只是第一步。如何把仿真里完美的"Scope波形"搬到真实的单片机上？如何处理真实传感器的噪声和漂移？

本项目基于STM32F103和高精度传感芯片INA226搭建了一套实物验证平台，完整实现了从底层数据清洗到EKF算法C语言移植的闭环。本文将手把手教你解决硬件通信的不确定性，并利用线性回归校准消除传感器误差，让你的算法在几十元的硬件上跑出实验室级的精度。

一、硬件平台：搭建你的"实物Simulink模型"

在仿真里，我们需要一个Solver(求解器)和一个Plant(被控对象)。在硬件世界里，它们对应如下：

求解器(MCU)：STM32F103RCT6

负责运行EKF算法矩阵运算，相当于Simulink里的步长(Step Size)设为0.1s。

传感器(Sensor)：INA226(高侧测量)

这就相当于仿真里的"Current Sensor"和"Voltage Sensor"模块。关键点：选用R100(0.1Ω)**采样电阻版本。相比常规的0.01Ω，它的信噪比更高，能捕捉到微安级的电流变化，这对SOC估算至关重要。

被控对象(Plant)：锂电池+负载，真实的非线性化学系统，而非数学模型。

1.1 电气连接拓扑

为了保证信号纯净，我们采用高侧采样方案(High-Side Sensing)。务必注意：INA226的VBS引脚必须与IN+短接，否则就像仿真里忘记连电压探头一样，读数恒为0。

二、底层攻关：解决"信号丢失"问题

在Simulink里连线是逻辑连接，但在硬件上，I2C总线常因阻抗匹配问题导致通信失败。

2.1 现象：地址漂移

部分INA226模块由于PCB设计原因，地址引脚A0/A1悬空。这导致I2C地址会随机跳变，就像仿真模型里的端口号一直在变，导致数据读取报错。

2.2 解决方案：自适应地址扫描算法

不要去动电烙铁。我们在初始化阶段加入一段**"握手轮询"**代码，自动寻找当前总线上响应的设备地址。

Matlab 复制代码

//bsp_ina226.c-自动扫描I2C地址
static uint8_t Current_INA_Addr=0x80;//默认地址

uint8_t INA226_Auto_Scan(void){
    uint8_t scan_addr;
    //遍历INA226数据手册规定的所有可能地址
    for(scan_addr=0x80;scan_addr<=0x9E;scan_addr+=2){
        I2C_Start();
        I2C_SendByte(scan_addr);//发送写命令试探
        
        if(I2C_WaitAck()==0){//收到ACK应答,说明找到设备
            I2C_Stop();
            printf("INA226 Found at: 0x%02X\n",scan_addr);
            Current_INA_Addr=scan_addr;//锁定该地址供后续读取
            return 1;
        }
        I2C_Stop();
        Delay_us(50);
    }
    return 0;//未找到设备
}

2.3 信号增强：推挽输出模式

仿真里没有"驱动能力"的概念，但STM32模拟I2C时，如果外部上拉电阻太大，波形上升沿会变缓导致丢包。我们将GPIO配置从标准的开漏输出(OD)改为推挽输出(PP)，利用单片机内部推力确保通信100%成功。

三、数据预处理：消除传感器系统误差

仿真里的传感器是理想的，但真实硬件存在ADC基准误差。实测发现，模块读数比高精度万用表偏高约5.7%（真值2.95V，读数3.12V）。这种线性误差会导致SOC估算的开路电压(OCV)查表严重偏离。
校准方法：增益修正(Gain Correction)

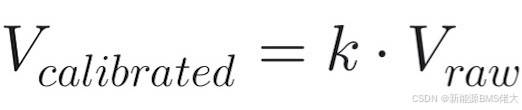
其中系数 k = 2.95 / 3.12 \approx 0.9455。

驱动层代码实现：

Matlab 复制代码

//获取校准后的电压值
float INA226_GetVoltage_Calibrated(void){
    uint16_t raw=INA226_ReadReg(REG_BUS_VOLTAGE);
    float voltage_raw=(float)raw*0.00125f;//LSB=1.25mV
    
    //软件线性补偿,消除系统误差
    return voltage_raw*0.9455f;
}

经过校准，电压误差被控制在**±0.01V**以内，满足了EKF对观测精度的要求。

四、算法移植：将MATLAB代码转为C语言

这是大家最熟悉的部分。我们将Simulink里的二阶RC模型离散化，并在MCU的while(1)循环中迭代。

4.1 算法流程映射

时间更新(Predict)：利用安时积分推算先验SOC。
测量更新(Correct)：比较"模型预测电压"与"INA226实测电压"，计算残差。
卡尔曼增益(K)：根据协方差矩阵P，决定信任模型还是信任传感器。

4.2 核心代码落地

我们在主循环中以**10Hz(100ms)**的频率运行算法：

Matlab 复制代码

int main(void){
    //系统初始化
    Hardware_Init();
    //初始化EKF,设定初始SOC为80%
    EKF_Init(&my_ekf,0.8f);

    while(1){
        //1.获取物理世界的观测值
        float vol=INA226_GetVoltage_Calibrated();
        float cur=INA226_GetCurrent();
        
        //2.EKF状态更新(相当于Simulink的一个Step)
        //输入:电流I(激励),电压V(响应)
        //输出:最优后验估计SOC
        float soc_ekf=EKF_Update(&my_ekf,cur,vol);
        
        //3.对照组:普通安时积分法
        g_AhSOC=Ah_Integration(cur,0.1f);//dt=0.1s

        //4.可视化显示
        LCD_Show_Data(vol,cur,soc_ekf,g_AhSOC);
        
        //严格控制采样周期为100ms
        Delay_ms(100);
    }
}

4.3 实验效果

可以看到，屏幕上绿色的**"INA226: OK"**代表硬件通信链路打通，Volt数据准确，EKF SOC正在根据电压回弹特性动态修正安时积分的误差。

五、总结

从仿真到实物，我们跨越了这几个坑：

不确定性：用软件扫描解决了硬件地址未定义的问题。
非理想性：用推挽输出解决了信号驱动能力不足的问题。
系统误差：用线性校准解决了廉价传感器的精度问题。
这就好比在Simulink里加入了一个**"Sensor Noise"模块和一个"Communication Delay"**模块，然后我们通过算法把它们抵消掉了。这才是嵌入式算法落地的魅力所在。
项目完整工程代码已打包，欢迎评论区交流！