Loss function

CIFAR-10

• 分类器输出的是 scores，不是概率

• 随机初始化的 W 基本是"瞎猜"，所以大多数列都是 bad

• 训练的目标，就是调整 W ，让 正确类别的 score 永远比其他类别高

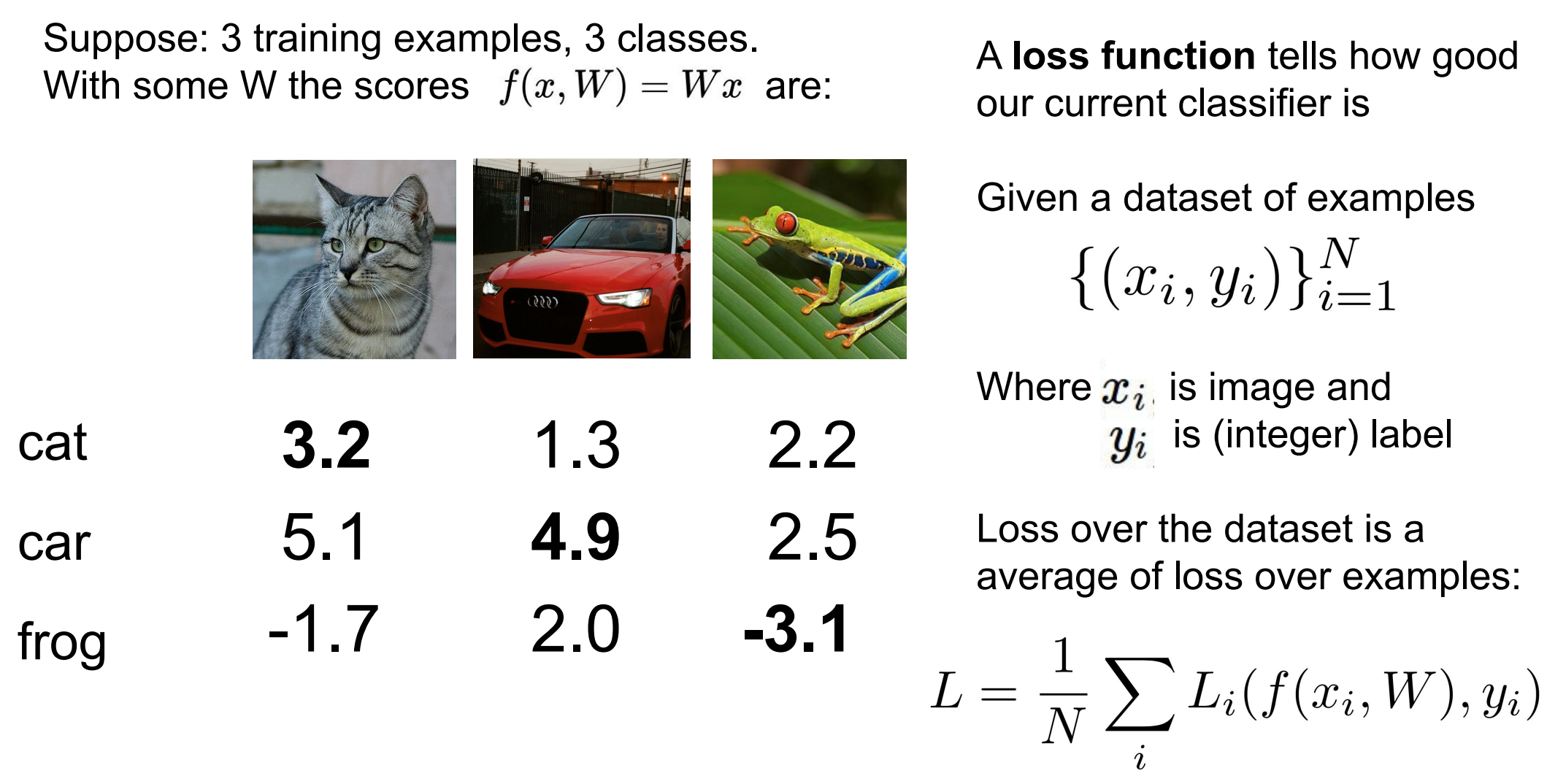
• score 只是"打分"，没有好坏尺度

• loss 把"预测对错 + 错得多严重"压缩成一个数

• 数据集 loss = 所有样本 loss 的平均

• 训练 = 调 W，让 loss 变小

Multiclass SVM loss

深度学习里的 SVM loss ≠ 传统 SVM 模型

• 对不对（classification）

  • 错 → 一定有 loss

• 错得有多离谱（ranking & margin）

  • 错得越多，loss 越大

• 对得是否"有把握"

  • 对了但 margin 不够，也会被罚

看图

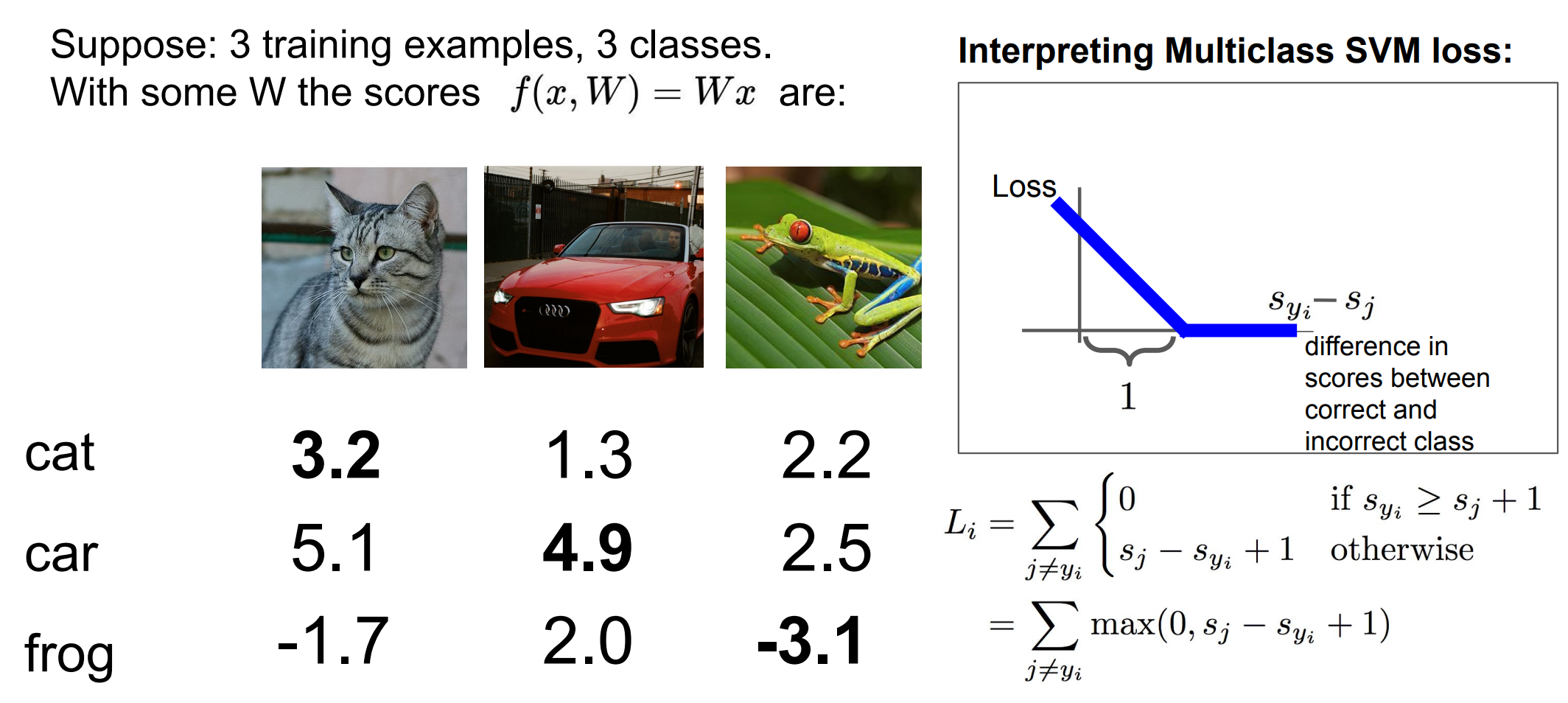
情况 1： s y i − s j ≥ 1 s_{y_i} - s_j \ge 1 syi−sj≥1

• 正确类别 明显赢了

• 蓝线在 0 上

• loss = 0

不罚，说明模型对这个类别"有把握"

情况 2： 0 < s y i − s j < 1 0 < s_{y_i} - s_j < 1 0<syi−sj<1

• 正确类别虽然更大，但 margin 不够

• loss 是正的

• 差得越少，罚得越多

预测对了，但不自信，也要罚

情况 3： s y i − s j ≤ 0 s_{y_i} - s_j \le 0 syi−sj≤0

• 错误类别 ≥ 正确类别

• 预测错

• loss 很大

预测错 + 错得离谱 → 重罚

计算过程

讨论改变

Q1: Car: 4.4

1. For the cat class :
   L cat = max ⁡ ( 0 , 1.3 − 4.4 + 1 ) = max ⁡ ( 0 , − 2.1 ) = 0 L_{\text{cat}} = \max(0, 1.3 - 4.4 + 1) = \max(0, -2.1) = 0 Lcat=max(0,1.3−4.4+1)=max(0,−2.1)=0

2. For the frog class:

   L frog = max ⁡ ( 0 , 2.0 − 4.4 + 1 ) = max ⁡ ( 0 , − 1.4 ) = 0 L_{\text{frog}} = \max(0, 2.0 - 4.4 + 1) = \max(0, -1.4) = 0 Lfrog=max(0,2.0−4.4+1)=max(0,−1.4)=0

Total Loss:

Since both of the incorrect classes (cat and frog) have a loss of 0, the total loss is:
L i = 0 + 0 = 0 L_i = 0 + 0 = 0 Li=0+0=0

Q2: What is the min/max possible SVM loss L i L_i Li​?

Maximum Loss:

• we want to maximize the difference s j − s y i + 1 s_j - s_{y_i} + 1 sj−syi+1 for each incorrect class j. This would happen if the correct class score is small (near 0) and the other class scores are large.

Minimum loss:

• we want the score of the correct class s y i s_{y_i} syi to be sufficiently larger than the other class scores s j s_j sj. This would ensure that the margin is positive, and thus the max ⁡ ( 0 , ⋅ ) \max(0, \cdot) max(0,⋅)term becomes 0 for all incorrect classes.

Q3: At initialization, W is small, so all s ≈ 0 s \approx 0 s≈0. What is the loss L i L_i Li, assuming N examples and C classes?

多分类 SVM 的单样本损失是：

L i = ∑ j ≠ y i max ⁡ ( 0 ,   s j − s y i + 1 ) L_i = \sum_{j \neq y_i} \max(0,\, s_j - s_{y_i} + 1) Li=j=yi∑max(0,sj−syi+1)

第一步：代入初始化条件

s j ≈ 0 , s y i ≈ 0 s_j \approx 0,\quad s_{y_i} \approx 0 sj≈0,syi≈0

所以对任意错误类别 j ≠ y i j \neq y_i j=yi：

s j − s y i + 1 = 0 − 0 + 1 = 1 s_j - s_{y_i} + 1 = 0 - 0 + 1 = 1 sj−syi+1=0−0+1=1

而
max ⁡ ( 0 , 1 ) = 1 \max(0, 1) = 1 max(0,1)=1

第二步：有多少项会被加进去？

• 一共有 C 个类别

• 正确类别是 1 个

• 错误类别是 C−1 个

所以：

L i = ∑ j ≠ y i 1 = C − 1 L_i = \sum_{j \neq y_i} 1 = C - 1 Li=j=yi∑1=C−1

全部 N 个样本的总 loss（不取平均）：

L = N ( C − 1 ) \boxed{L = N(C - 1)} L=N(C−1)

如果是平均 loss（常见实现）：

1 N ∑ i L i = C − 1 \boxed{\frac{1}{N}\sum_i L_i = C - 1} N1i∑Li=C−1

Q4: 如果求和不排除正确类别 j = y i j=y_i j=yi​，会发生什么?

• SVM 的思想是：
  "正确类别要比错误类别至少大 1"

• 正确类别不应该和自己比较

• 否则模型会：

  • 永远无法把 loss 降到 0

  • 即使已经完美分类，也会被强制惩罚 1

Q5 ：原来每个样本的 loss 是把所有错误类别的 hinge 违约量 相加（sum） ，那如果改成 取平均（mean） 会怎样。

标准（sum）：

L i = ∑ j ≠ y i max ⁡ ( 0 ,    s j − s y i + 1 ) L_i=\sum_{j\neq y_i}\max(0,\; s_j-s_{y_i}+1) Li=j=yi∑max(0,sj−syi+1)

改成 mean（对错误类别取平均）：

L i mean = 1 C − 1 ∑ j ≠ y i max ⁡ ( 0 ,    s j − s y i + 1 ) = L i C − 1 L_i^{\text{mean}}=\frac{1}{C-1}\sum_{j\neq y_i}\max(0,\; s_j-s_{y_i}+1)=\frac{L_i}{C-1} Limean=C−11j=yi∑max(0,sj−syi+1)=C−1Li

在这张图里 C=3⇒C−1=2,所以 mean 就是把原来的 loss 除以 2。

• 第 1 个样本：原来 L 1 = 2.9 L_1=2.9 L1=2.9，mean 后

  L 1 mean = 2.9 2 = 1.45 L_1^{\text{mean}}=\frac{2.9}{2}=1.45 L1mean=22.9=1.45

• 第 2 个样本：原来 L 2 = 0 _2=0 2=0，mean 后还是 0

• 第 3 个样本：原来 L 3 = 12.9 L_3=12.9 L3=12.9，mean 后
  L 3 mean = 12.9 2 = 6.45 L_3^{\text{mean}}=\frac{12.9}{2}=6.45 L3mean=212.9=6.45

直观上：mean 不会改变"谁违反了 margin、违反多少"的相对关系，只是把尺度缩小了 ；训练时等价于把梯度整体缩放了一个常数这里是 1 2 \tfrac{1}{2} 21，通常可以通过学习率/正则系数一起调整来抵消

Q6 把原来的 hinge loss（一次） 改成 squared hinge loss（二次 hinge） ：把每个违反间隔的量先算出来，再平方后求和。

原来（一次 hinge）：
L i = ∑ j ≠ y i max ⁡ ( 0 , Δ j ) , Δ j = s j − s y i + 1 L_i=\sum_{j\neq y_i}\max(0,\Delta_j),\quad \Delta_j=s_j-s_{y_i}+1 Li=j=yi∑max(0,Δj),Δj=sj−syi+1

现在（平方 hinge）：

L i ( 2 ) = ∑ j ≠ y i ( max ⁡ ( 0 , Δ j ) ) 2 L_i^{(2)}=\sum_{j\neq y_i}\big(\max(0,\Delta_j)\big)^2 Li(2)=j=yi∑(max(0,Δj))2

它的含义很直接：

• 如果某个错误类别没违反间隔 Δ j ≤ 0 \Delta_j\le 0 Δj≤0，那一项还是 0；

• 如果违反了 Δ j > 0 \Delta_j>0 Δj>0，原来惩罚是 Δ j \Delta_j Δj，现在变成 Δ j 2 \Delta_j^2 Δj2，**大错被惩罚得更重，小错惩罚更温和

Q7: Suppose that we found a W such that L = 0. Is this W unique?

2W 也能导致L=0，不唯一

代码实现

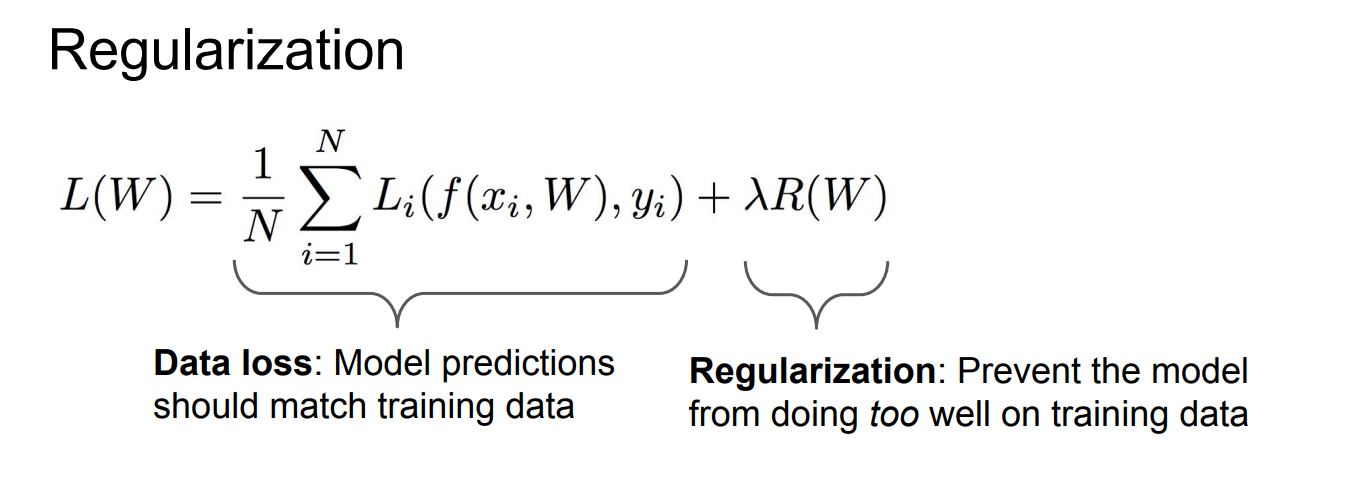
Regularization

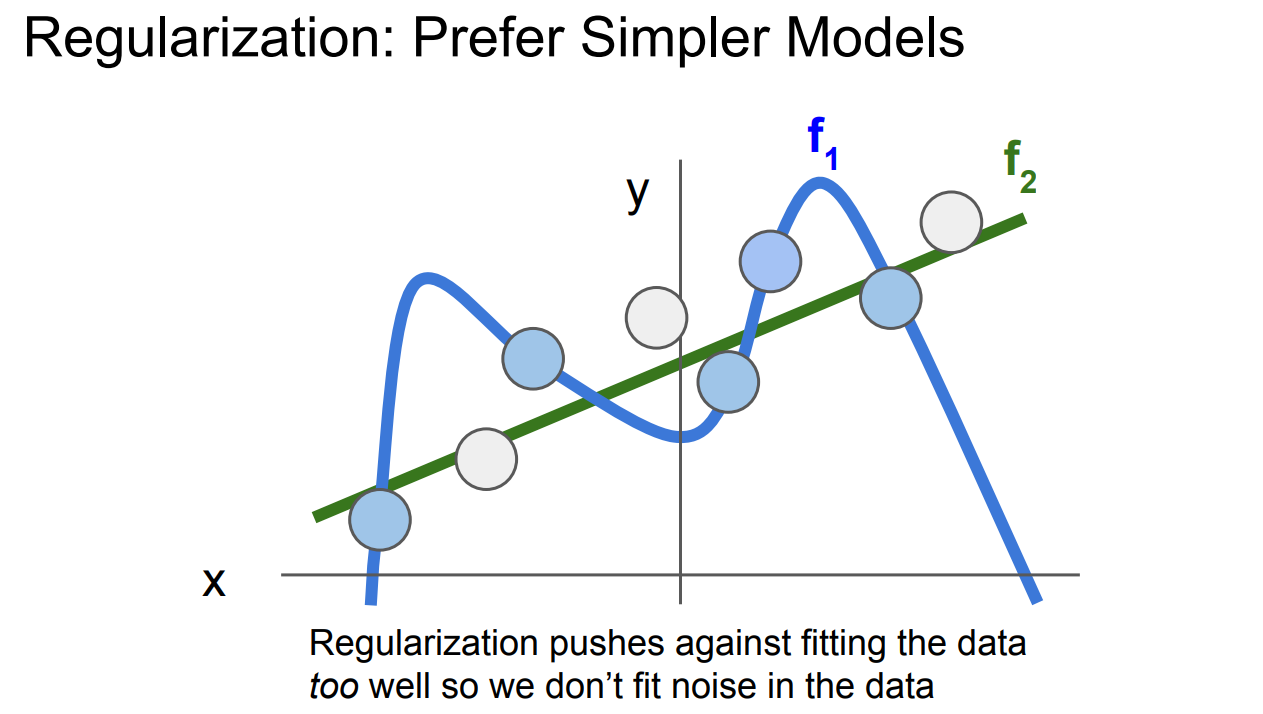
• **图中有两个模型 ：

  • f 1 f_1 f1 是一个过拟合的模型，试图通过曲线精确拟合每个数据点，包括数据中的噪声点（即图中的"白色点"）。这种情况意味着模型复杂，容易将数据中的随机噪声也当作规律来拟合，导致模型对训练数据的适应性很好，但对新数据的泛化能力差。

  • f 2 f_2 f2是一个更简单的模型，它并不精确拟合每一个数据点，而是通过一条平滑的直线尽量简化拟合。这样的模型避免了过度拟合，减少了对数据噪声的敏感性，从而更可能具有更好的泛化能力。

正则化的作用：

• 正则化 通过惩罚复杂的模型 ，避免它们过度拟合训练数据。这样，模型在优化过程中会倾向于选择更简单的结构，从而避免了对数据中的噪声进行过多拟合

• 正则化控制了模型的复杂性，使得它更好地捕捉到数据的真实模式，而不是偶然的噪声。

Why regularize?

• Express preferences over weights
• Make the model simple so it works on test data
• Improve optimization by adding curvature

偏好

对 L2 正则化 而言，惩罚的是平方范数， ∣ w 1 ∣ 2 2 = 1 |w_1|_2^2=1 ∣w1∣22=1，而 ∣ w 2 ∣ 2 2 = 4 × 0.25 2 = 0.25 |w_2|_2^2=4\times 0.25^2=0.25 ∣w2∣22=4×0.252=0.25，因此 L2 明显更偏好 w 2 w_2 w2，体现了"把权重分散开、避免单个权重过大"的偏好；

相反，对 L1 正则化 ，惩罚的是绝对值之和， ∣ w 1 ∣ 1 = 1 |w_1|_1=1 ∣w1∣1=1， ∣ w 2 ∣ 1 = 1 |w_2|_1=1 ∣w2∣1=1，在这个特定例子中二者惩罚相同，因此 L1 不会区分它们，但从整体性质上看，L1 的几何结构更倾向于产生稀疏解，通常会偏好像 w 1 w_1 w1 这样"少数非零、其余为零"的权重结构。

Softmax classifier

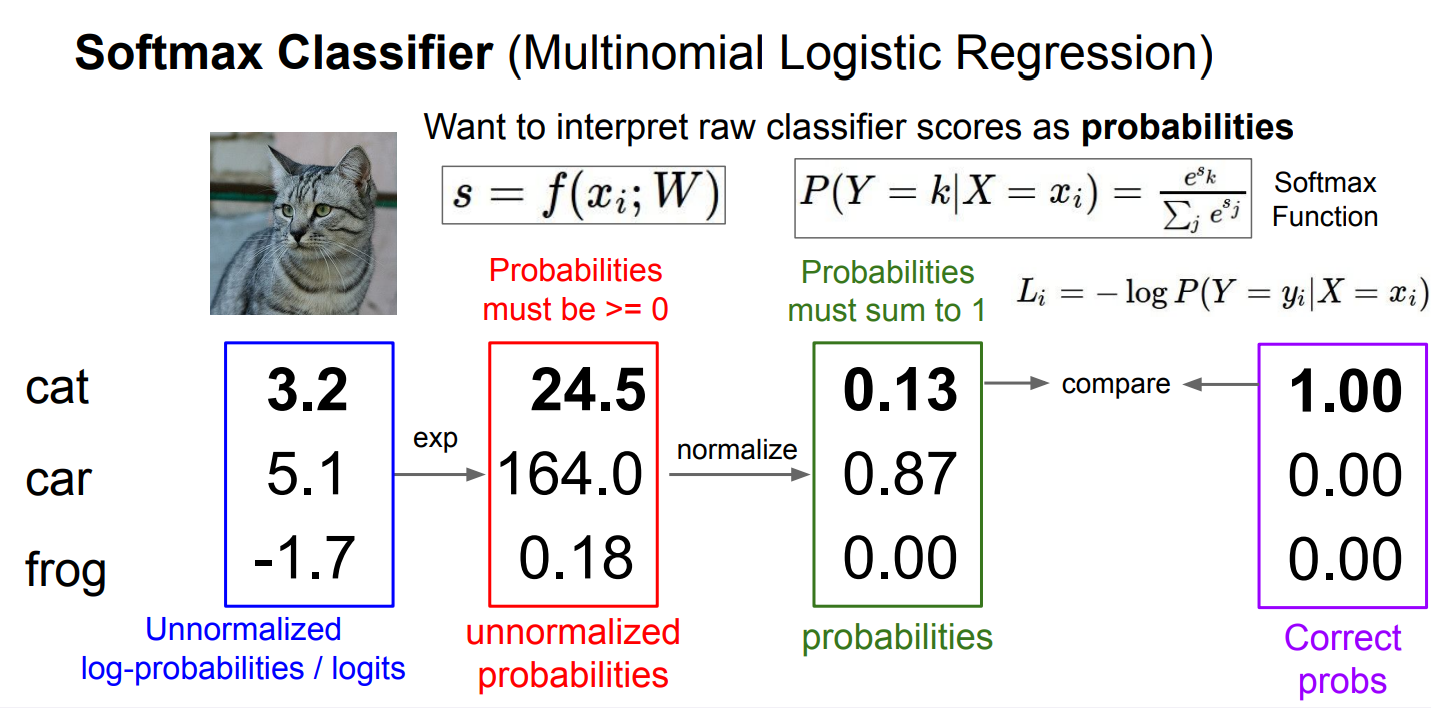
Softmax 分类器把原始打分（logits）一步步变成概率并计算损失 的全过程：

首先模型对输入 x i x_i xi 给出每个类别的原始分数 s = f ( x i ; W ) s=f(x_i;W) s=f(xi;W)，这里分别是 cat: (3.2)、car: (5.1)、frog: (-1.7)，这些数可以是任意实数，本身不是概率；

接着对每个分数取指数，得到非负的"未归一化概率" e 3.2 ≈ 24.5 e^{3.2}\approx24.5 e3.2≈24.5, e 5.1 ≈ 164.0 e^{5.1}\approx164.0 e5.1≈164.0、 e − 1.7 ≈ 0.18 e^{-1.7}\approx0.18 e−1.7≈0.18，指数操作保证数值 ≥ 0 \ge0 ≥0；

然后做归一化，用每一类的指数值除以它们的总和 24.5 + 164.0 + 0.18 ≈ 188.68 24.5+164.0+0.18\approx188.68 24.5+164.0+0.18≈188.68，得到真正的概率分布：
P ( cat ) ≈ 24.5 / 188.68 ≈ 0.13 P(\text{cat})\approx24.5/188.68\approx0.13 P(cat)≈24.5/188.68≈0.13，
P ( car ) ≈ 164.0 / 188.68 ≈ 0.87 P(\text{car})\approx164.0/188.68\approx0.87 P(car)≈164.0/188.68≈0.87，
P ( frog ) ≈ 0.18 / 188.68 ≈ 0.001 P(\text{frog})\approx0.18/188.68\approx0.001 P(frog)≈0.18/188.68≈0.001（图中约写为 0.00），

这一步保证所有概率之和为 1；

最后如果真实标签是 cat，就取对应概率计算交叉熵损失( L i = − log ⁡ P ( Y = cat ∣ X = x i ) = − log ⁡ ( 0.13 ) ≈ 2.04 L_i=-\log P(Y=\text{cat}\mid X=x_i)=-\log(0.13)\approx2.04 Li=−logP(Y=cat∣X=xi)=−log(0.13)≈2.04，

从最大似然角度看，这等价于通过调整权重 (W) 来最大化真实类别在 softmax 概率下出现的可能性。

在训练时我们只关注模型给出的真实类别的预测概率 P ( Y = y i ∣ X = x i ) P(Y = y_i \mid X = x_i) P(Y=yi∣X=xi)，并根据这个概率计算损失值。

对于其他类别（如 car 和 frog），我们不会直接计算它们的损失值，而是通过整体损失来优化模型。

因此，损失值 L i L_i Li​ 只与 真实标签 对应的类别相关

信息论角度

用信息论视角解释 softmax + 交叉熵损失 ，核心在于：模型输出的概率分布 Q（绿色列）与真实标签对应的"目标分布" P（紫色列，one-hot 向量）之间如何度量差异；紫色的 ([1,0,0]) 表示真实分布 P ------样本真实类别是 cat，因此 P ( cat ) = 1 P(\text{cat})=1 P(cat)=1，其余为 0，而绿色的是模型预测分布 Q；

上图用 KL 散度 表达这种比较： D K L ( P ∣ Q ) = ∑ y P ( y ) log ⁡ P ( y ) Q ( y ) D_{\mathrm{KL}}(P|Q)=\sum_y P(y)\log\frac{P(y)}{Q(y)} DKL(P∣Q)=∑yP(y)logQ(y)P(y)，由于 P 是 one-hot，只有真实类别那一项不为零，因此 KL 散度等价于 − log ⁡ Q ( y true -\log Q(y_{\text{true}} −logQ(ytrue)加上一个常数；

下图进一步指出训练时实际使用的是 交叉熵 H ( P , Q ) = H ( P ) + D K L ( P ∣ Q ) H(P,Q)=H(P)+D_{\mathrm{KL}}(P|Q) H(P,Q)=H(P)+DKL(P∣Q)，而对 one-hot 标签来说 H ( P ) = 0 H(P)=0 H(P)=0，于是交叉熵就完全等价于负对数似然 L i = − log ⁡ P ( Y = y i ∣ X = x i ) L_i=-\log P(Y=y_i\mid X=x_i) Li=−logP(Y=yi∣X=xi)，

这也从信息论角度解释了为什么 softmax 分类器只"算真实类别那一项"，以及为什么它既可以被看作最大似然估计，又可以被看作在最小化预测分布与真实分布之间的信息差距。

似然和交叉熵

似然（likelihood） 是"从模型角度看数据有多合理"的概率量。

而交叉熵（cross-entropy） 是"从信息论角度度量两个分布有多不一致"的期望信息量；

在 softmax 分类 + one-hot 标签这个特例下，两者在数值上等价，但概念来源不同。

具体地说，似然关注的是单个样本真实标签在模型分布下出现的概率
P ( Y = y i ∣ X = x i ) P(Y=y_i\mid X=x_i) P(Y=yi∣X=xi)

训练时我们做极大似然，就是让这个概率尽可能大；

为了方便优化，取负对数得到 ( L i L_i Li：第 i 个样本的损失)
− log ⁡ P ( Y = y i ∣ X = x i ) -\log P(Y=y_i\mid X=x_i) −logP(Y=yi∣X=xi)

而交叉熵定义为 H ( P , Q ) = − ∑ y P ( y ) log ⁡ Q ( y ) H(P,Q)=-\sum_y P(y)\log Q(y) H(P,Q)=−y∑P(y)logQ(y)它本来是"如果真实分布是 P，却用 Q 来编码，平均要花多少比特"；

当监督学习中真实分布 P 是 one-hot（正确类别概率为 1，其余为 0）时，这个求和只剩下一项，正好变成 − log ⁡ Q ( y i ) -\log Q(y_i) −logQ(yi)。

因此：统计学语言，这是负对数似然；从信息论语言，这是交叉熵；从直觉上看，它是"模型对真实标签有多意外"的自信息**。区别不在公式，而在视角：似然强调"解释数据"，交叉熵强调"分布不匹配的代价"，

学科	名字	视角	数学形式
概率统计	负对数似然	数据是否由模型生成	− ∑ i log ⁡ P ( y i ∣ x i ) -\sum_i \log P(y_i\mid x_i) −∑ilogP(yi∣xi)
信息论	交叉熵	分布不匹配的代价	H ( P , Q ) H(P,Q) H(P,Q)
信息论	KL 散度	编码冗余	D K L ( P ∣ Q ) D_{\mathrm{KL}}(P|Q) DKL(P∣Q)
机器学习	loss / loss function	优化目标	1 n ∑ i L i \frac{1}{n}\sum_i L_i n1∑iLi

问题讨论

Q1: 取值范围

这里把 softmax + 负对数似然损失 写成统一形式

L i = − log ⁡ e s y i ∑ j e s j L_i=-\log\frac{e^{s_{y_i}}}{\sum_j e^{s_j}} Li=−log∑jesjesyi

首先，softmax 给出的是真实类别的预测概率 p y i ∈ ( 0 , 1 ] p_{y_i}\in(0,1] pyi∈(0,1]，因此损失 L i = − log ⁡ p y i L_i=-\log p_{y_i} Li=−logpyi 的最小值 在模型把全部概率都分给正确类别时取得，即 p y i = 1 p_{y_i}=1 pyi=1，此时 L i = 0 L_i=0 Li=0；而最大值 在 p y i → 0 p_{y_i}\to 0 pyi→0 时出现， − log ⁡ p y i → + ∞ -\log p_{y_i}\to +\infty −logpyi→+∞，因此 softmax loss 下界为 0、上界无穷大。

Q2:初始化时大小的直观问题

在随机初始化阶段，各类别打分 s_j 近似相等，softmax 后每一类的概率都接近 1/C（C 为类别数），于是单样本的初始损失为

L i = − log ⁡ 1 C = log ⁡ C L_i=-\log\frac{1}{C}=\log C Li=−logC1=logC

这也是训练开始时常见的 loss 量级来源：比如 CIFAR-10(C=10）初始 loss 约为 log ⁡ 10 ≈ 2.30 \log 10\approx 2.30 log10≈2.30，ImageNet(C=1000）则约为 log ⁡ 1000 ≈ 6.91 \log 1000\approx 6.91 log1000≈6.91。

两种loss比较

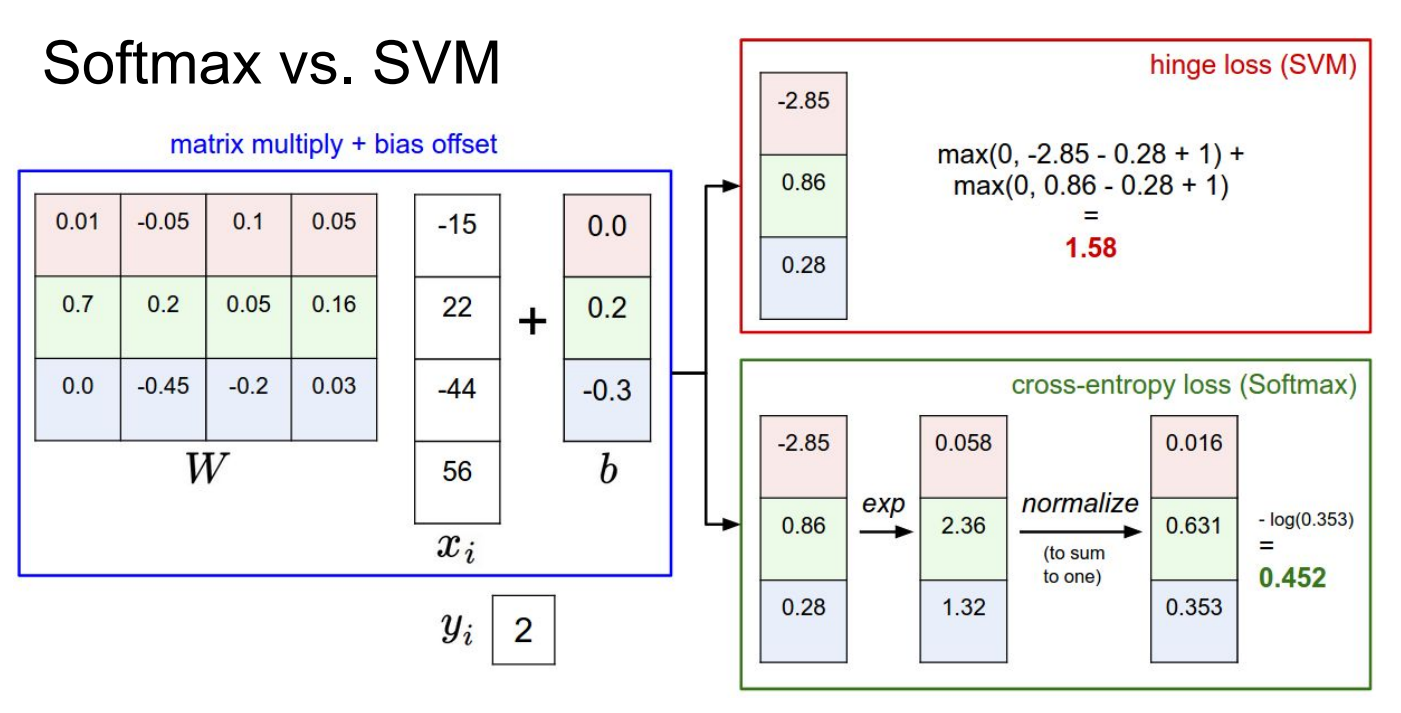
Q1.多分类 SVM（hinge）loss

L i = ∑ j ≠ y i max ⁡ ( 0 , ; s j − s y i + 1 ) L_i=\sum_{j\neq y_i}\max\bigl(0,; s_j - s_{y_i} + 1\bigr) Li=j=yi∑max(0,;sj−syi+1)

其中真实类别 y i = 0 y_i=0 yi=0，所以 s y i = s 0 s_{y_i}=s_0 syi=s0。对每一组 scores 分别代入即可：

第一组 ([10,-2,3])，真实分数是 10，两个错误类的 margin 分别为 (-2-10+1=-11) 和 (3-10+1=-6)，都小于 0，因此两项都为 0，整体 SVM loss 为 0；

第二组 ([10,9,9])，真实分数仍是 10，两个错误类的 margin 为 (9-10+1=0) 和 (9-10+1=0)，(\max(0,0)=0)，因此 loss 仍为 0，说明"刚好满足 margin 要求也不罚"；

第三组 ([10,-100,-100])，两个错误类的 margin 为 (-100-10+1=-109) 和 (-100-10+1=-109)，同样都为 0，loss 还是 0。这个例子清楚地体现了 SVM loss 的特性：
只要正确类别比分错误类别至少大 1（margin），就完全不再关心分数有多大，这与 softmax loss"概率越接近 1 越好、永远有梯度"的行为形成鲜明对比。

Q2:Is the Softmax loss zero for any of them?

结论先给出：这三组里，Softmax loss 对任何一组都不可能是 0。

先说 Softmax loss 什么时候等于 0（理论条件）

Softmax loss（对单样本）是

L i = − log ⁡ e s y i ∑ j e s j L_i=-\log\frac{e^{s_{y_i}}}{\sum_j e^{s_j}} Li=−log∑jesjesyi

要让 L i = 0 L_i=0 Li=0，必须满足
e s y i ∑ j e s j = 1 \frac{e^{s_{y_i}}}{\sum_j e^{s_j}}=1 ∑jesjesyi=1

而这等价于：

e s y i ≫ e s j ∀ j ≠ y i e^{s_{y_i}} \gg e^{s_j}\quad \forall j\neq y_i esyi≫esj∀j=yi

严格说：

• 只有当 s y i − s j → + ∞ s_{y_i}-s_j\to +\infty syi−sj→+∞ 时，Softmax loss 才能趋近 0

• 在任何有限分数下，Softmax loss 都 > 0

Softmax loss 的 0 只是"极限值"，不是可达值

对你给的三组 scores 逐一判断

真实类别： y i = 0 y_i=0 yi=0

第一组：([10,-2,3])

Softmax 概率：
P ( y = 0 ) = e 10 e 10 + e − 2 + e 3 < 1 P(y=0)=\frac{e^{10}}{e^{10}+e^{-2}+e^{3}}<1 P(y=0)=e10+e−2+e3e10<1

第二组：([10,9,9])

P ( y = 0 ) = e 10 e 10 + e 9 + e 9 P(y=0)=\frac{e^{10}}{e^{10}+e^9+e^9} P(y=0)=e10+e9+e9e10

第三组：([10,-100,-100])

这是最"极端"的一组：

P ( y = 0 ) ≈ e 10 e 10 + 2 e − 100 ≈ 1 P(y=0)\approx\frac{e^{10}}{e^{10}+2e^{-100}}\approx 1 P(y=0)≈e10+2e−100e10≈1