决策树简介 -- 生活中的决策树
女孩相亲的决策树
女儿:多大年纪了?
母亲:26。
女儿:长的帅不帅?
母亲:挺帅的。
女儿:收入高不?
母亲:不算很高，中等情况。
女儿:是公务员不?
母亲:是，在税务局上班呢。
女儿:那好，我去见见。
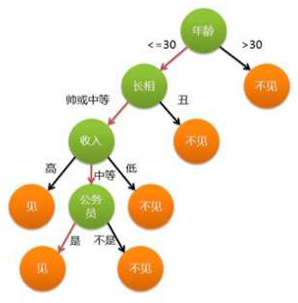
决策树是一种树形结构，树中每个内部节点表示一个特征上的判断，每个分支代表一个判断结果的输出， 每个叶子节点代表一种分类结果。
决策树的建立过程
-
特征选择：选取有较强分类能力的特征。
-
决策树生成：根据选择的特征生成决策树。
-
决策树也易过拟合，采用剪枝的方法缓解过拟合。
信息熵
• 熵 Entropy ： 信息论中代表随机变量不确定度的度量
• 熵越大，数据的不确定性越高，信息就越多
• 熵越小，数据的不确定性越低
• 计算方法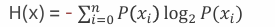 
，其中 P(xi) 表示数据中类别出现的概率，H(x) 表示信息的信息熵值。
例
1：计算数据 α（ABCDEFGH） 信息熵，其中A、B、C、D、E、F、G、H 出现的概率为：1/8。
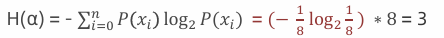
2：计算数据 β（AAAABBCD） 信息熵 其中A 出现的概率为1/2，B 出现的概率为1/4，C、D 出现的概率为1/8
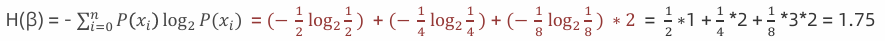
3：假如数据集有三个类别，分别占比为：{⅓, ⅓, ⅓}，信息熵：
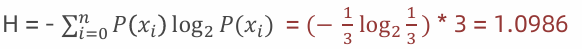
4：假如数据集有三个类别，分别占比为：{1/10, 2/10, 7/10}，信息熵：
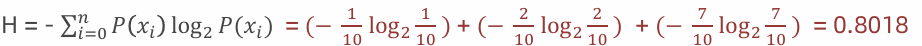
5：假如数据集有三个类别，分别占比为：{1, 0, 0}，信息熵：
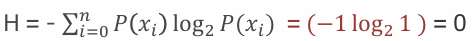
信息增益
概念
信息增益是指 ，使用某个特征A对数据集D进行划分后，系统不确定性减少的程度 。换句话说，就是"这个特征能为分类带来多少信息"。决策树的构建本质上就是在递归地计算信息增益 的过程。特征a对训练数据集D的信息增益𝐺𝑎𝑖𝑛(𝐷, 𝑎)或g(D，a)，定义为集合D的熵H(D)与特征a给定条件下D的熵H(D | a)之差。条件熵（加权平均熵） ，也用于度量一个数据集合的混乱程度 或不确定性。其物理意义是"为了消除不确定性所需的信息量"。
数学公式：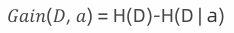
，信息增益 = 熵 -条件熵。
条件熵（加权平均熵）
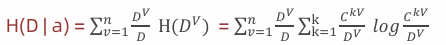
例
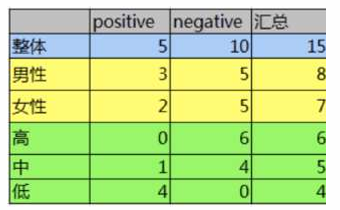
• 已知 某一个论坛客户流失率数据
• 需求 考察性别、活跃度特征哪一个特征对流失率的影响更大
• 分析
✓ 15条样本：5个正样本、10个负样本
✓ 1 计算熵
✓ 2 计算性别信息增益
✓ 3 计算活跃度信息增益
✓ 4 比较两个特征的信息增益
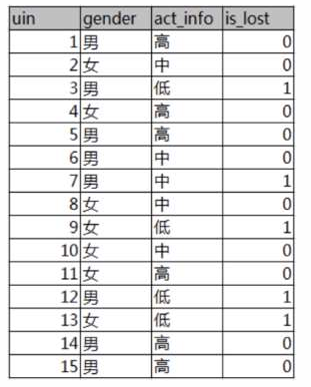
计算熵：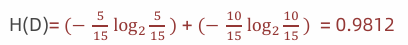
计算性别条件熵(a="性别")
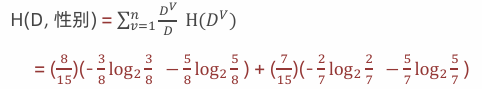
计算性别信息增益(a="性别")
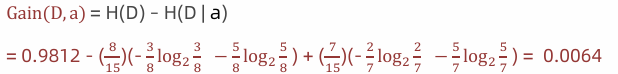
计算活跃度条件熵(a="活跃度")
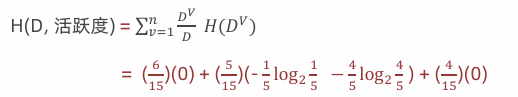
计算活跃度信息增益(a="活跃度")
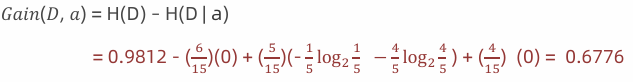
结论：活跃度的信息增益比性别的信息增益大，对用户流失的影响比性别大。
完整数学计算流程
数据集示例（经典的打球决策）
| 序号 | 天气(Outlook) | 温度(Temp) | 湿度(Humidity) | 风力(Wind) | 打球(Play) |
|---|---|---|---|---|---|
| 1 | Sunny | Hot | High | Weak | No |
| 2 | Sunny | Hot | High | Strong | No |
| 3 | Overcast | Hot | High | Weak | Yes |
| 4 | Rainy | Mild | High | Weak | Yes |
| 5 | Rainy | Cool | Normal | Weak | Yes |
| 6 | Rainy | Cool | Normal | Strong | No |
| 7 | Overcast | Cool | Normal | Strong | Yes |
| 8 | Sunny | Mild | High | Weak | No |
| 9 | Sunny | Cool | Normal | Weak | Yes |
| 10 | Rainy | Mild | Normal | Weak | Yes |
| 11 | Sunny | Mild | Normal | Strong | Yes |
| 12 | Overcast | Mild | High | Strong | Yes |
| 13 | Overcast | Hot | Normal | Weak | Yes |
| 14 | Rainy | Mild | High | Strong | No |
统计：共14个样本，Yes=9，No=5
第1步：计算根节点的熵（整个数据集）
首先计算目标变量"Play"的熵：
-
P(Yes) = 9/14 ≈ 0.643
-
P(No) = 5/14 ≈ 0.357
Entropy(S) = -[P(Yes) × log₂(P(Yes)) + P(No) × log₂(P(No))]
= -[0.643 × log₂(0.643) + 0.357 × log₂(0.357)]
= -[0.643 × (-0.637) + 0.357 × (-1.487)] // log₂计算
= -[-0.410 - 0.531]
= 0.941
根节点熵 ：Entropy(S) = 0.941
第2步：计算每个特征的信息增益
2.1 特征：天气(Outlook)
天气有三个取值：Sunny(5个), Overcast(4个), Rainy(5个)
a) Sunny分支 (5个样本：Yes=2, No=3)
P(Yes|Sunny) = 2/5 = 0.4 P(No|Sunny) = 3/5 = 0.6 Entropy(Sunny) = -[0.4×log₂(0.4) + 0.6×log₂(0.6)] = -[0.4×(-1.322) + 0.6×(-0.737)] = -[-0.529 - 0.442] = 0.971
b) Overcast分支 (4个样本：Yes=4, No=0)
P(Yes|Overcast) = 4/4 = 1.0
P(No|Overcast) = 0/4 = 0.0
Entropy(Overcast) = -[1.0×log₂(1.0) + 0.0×log₂(0.0)]
= -[1.0×0 + 0] // log₂(1)=0, log₂(0)未定义但权重为0
= 0c) Rainy分支 (5个样本：Yes=3, No=2)
P(Yes|Rainy) = 3/5 = 0.6
P(No|Rainy) = 2/5 = 0.4
Entropy(Rainy) = -[0.6×log₂(0.6) + 0.4×log₂(0.4)]
= -[0.6×(-0.737) + 0.4×(-1.322)]
= -[-0.442 - 0.529]
= 0.971d) 计算加权平均熵
权重(Sunny) = 5/14 ≈ 0.357
权重(Overcast) = 4/14 ≈ 0.286
权重(Rainy) = 5/14 ≈ 0.357
平均熵 = (5/14)×0.971 + (4/14)×0 + (5/14)×0.971
= 0.357×0.971 + 0.286×0 + 0.357×0.971
= 0.347 + 0 + 0.347
= 0.694e) 信息增益
Gain(S, Outlook) = Entropy(S) - 平均熵
= 0.941 - 0.694
= 0.2472.2 特征：温度(Temp)
温度有三个取值：Hot(4个), Mild(6个), Cool(4个)
a) Hot分支 (4个样本：Yes=2, No=2)
P(Yes|Hot) = 2/4 = 0.5
P(No|Hot) = 2/4 = 0.5
Entropy(Hot) = -[0.5×log₂(0.5) + 0.5×log₂(0.5)]
= -[0.5×(-1) + 0.5×(-1)]
= -[-0.5 - 0.5]
= 1.0b) Mild分支 (6个样本：Yes=4, No=2)
P(Yes|Mild) = 4/6 ≈ 0.667
P(No|Mild) = 2/6 ≈ 0.333
Entropy(Mild) = -[0.667×log₂(0.667) + 0.333×log₂(0.333)]
= -[0.667×(-0.585) + 0.333×(-1.585)]
= -[-0.390 - 0.528]
= 0.918c) Cool分支 (4个样本：Yes=3, No=1)
P(Yes|Cool) = 3/4 = 0.75
P(No|Cool) = 1/4 = 0.25
Entropy(Cool) = -[0.75×log₂(0.75) + 0.25×log₂(0.25)]
= -[0.75×(-0.415) + 0.25×(-2.0)]
= -[-0.311 - 0.5]
= 0.811d) 加权平均熵
平均熵 = (4/14)×1.0 + (6/14)×0.918 + (4/14)×0.811
= 0.286×1.0 + 0.429×0.918 + 0.286×0.811
= 0.286 + 0.394 + 0.232
= 0.912e) 信息增益
Gain(S, Temp) = 0.941 - 0.912 = 0.0292.3 特征：湿度(Humidity)
湿度有两个取值：High(7个), Normal(7个)
a) High分支 (7个样本：Yes=3, No=4)
P(Yes|High) = 3/7 ≈ 0.429
P(No|High) = 4/7 ≈ 0.571
Entropy(High) = -[0.429×log₂(0.429) + 0.571×log₂(0.571)]
= -[0.429×(-1.222) + 0.571×(-0.808)]
= -[-0.524 - 0.461]
= 0.985b) Normal分支 (7个样本：Yes=6, No=1)
P(Yes|Normal) = 6/7 ≈ 0.857
P(No|Normal) = 1/7 ≈ 0.143
Entropy(Normal) = -[0.857×log₂(0.857) + 0.143×log₂(0.143)]
= -[0.857×(-0.222) + 0.143×(-2.807)]
= -[-0.190 - 0.401]
= 0.591c) 加权平均熵
平均熵 = (7/14)×0.985 + (7/14)×0.591
= 0.5×0.985 + 0.5×0.591
= 0.493 + 0.296
= 0.789d) 信息增益
Gain(S, Humidity) = 0.941 - 0.789 = 0.1522.4 特征：风力(Wind)
风力有两个取值：Weak(8个), Strong(6个)
a) Weak分支 (8个样本：Yes=6, No=2)
P(Yes|Weak) = 6/8 = 0.75
P(No|Weak) = 2/8 = 0.25
Entropy(Weak) = -[0.75×log₂(0.75) + 0.25×log₂(0.25)]
= -[0.75×(-0.415) + 0.25×(-2.0)]
= -[-0.311 - 0.5]
= 0.811b) Strong分支 (6个样本：Yes=3, No=3)
P(Yes|Strong) = 3/6 = 0.5
P(No|Strong) = 3/6 = 0.5
Entropy(Strong) = -[0.5×log₂(0.5) + 0.5×log₂(0.5)]
= -[0.5×(-1) + 0.5×(-1)]
= -[-0.5 - 0.5]
= 1.0c) 加权平均熵
平均熵 = (8/14)×0.811 + (6/14)×1.0
= 0.571×0.811 + 0.429×1.0
= 0.463 + 0.429
= 0.892d) 信息增益
Gain(S, Wind) = 0.941 - 0.892 = 0.049第3步：选择根节点特征
比较所有增益：
Gain(Outlook) = 0.247 ← 最大
Gain(Humidity) = 0.152
Gain(Wind) = 0.049
Gain(Temp) = 0.029选择 Outlook 作为根节点，因为它信息增益最大。
现在树的结构开始形成：
[Outlook]
/ | \
Sunny Overcast Rainy
(5个) (4个) (5个)第4步：递归处理各个分支
4.1 分支：天气Outlook = Overcast
数据子集（4个样本）：
序号 温度 湿度 风力 Play
3 Hot High Weak Yes
7 Cool Normal Strong Yes
12 Mild High Strong Yes
13 Hot Normal Weak Yes计算：
-
Yes = 4, No = 0
-
P(Yes) = 4/4 = 1.0
-
P(No) = 0/4 = 0.0
-
Entropy(Overcast) = -[1.0×log₂(1.0) + 0.0×log₂(0.0)] = 0
判定：
-
节点纯净（熵=0）
-
创建叶子节点：Play = Yes
4.2 分支：天气Outlook = Sunny
数据子集（5个样本）：
序号 温度 湿度 风力 Play
1 Hot High Weak No
2 Hot High Strong No
8 Mild High Weak No
9 Cool Normal Weak Yes
11 Mild Normal Strong Yes4.2.1 计算Sunny分支的熵
-
Yes = 2, No = 3
-
P(Yes) = 2/5 = 0.4
-
P(No) = 3/5 = 0.6
-
Entropy(S_sunny) = -[0.4×log₂(0.4) + 0.6×log₂(0.6)] = 0.971
4.2.2 计算剩余特征的信息增益
a) 特征：湿度Humidity (在Sunny分支)
-
High: 3个样本（全部No）
-
Normal: 2个样本（全部Yes）
Entropy(High|Sunny) = -[P(Yes)×log₂(P(Yes)) + P(No)×log₂(P(No))]
= -[0×log₂(0) + 1×log₂(1)] = 0（全是No）
Entropy(Normal|Sunny) = -[P(Yes)×log₂(P(Yes)) + P(No)×log₂(P(No))]
= -[1×log₂(1) + 0×log₂(0)] = 0（全是Yes）
权重(High) = 3/5 = 0.6
权重(Normal) = 2/5 = 0.4
加权平均熵 = 0.6×0 + 0.4×0 = 0
Gain(Sunny, Humidity) = Entropy(S_sunny) - 加权平均熵
= 0.971 - 0 = 0.971b) 特征：温度Temp (在Sunny分支)
-
Hot: 2个样本（全部No）
-
Mild: 2个样本（1Yes, 1No）
-
Cool: 1个样本（1Yes, 0No）
# Hot分支
P(Yes|Hot) = 0/2 = 0, P(No|Hot) = 2/2 = 1
Entropy(Hot|Sunny) = -[0×log₂(0) + 1×log₂(1)] = 0
# Mild分支
P(Yes|Mild) = 1/2 = 0.5, P(No|Mild) = 1/2 = 0.5
Entropy(Mild|Sunny) = -[0.5×log₂(0.5) + 0.5×log₂(0.5)] = 1.0
# Cool分支
P(Yes|Cool) = 1/1 = 1, P(No|Cool) = 0/1 = 0
Entropy(Cool|Sunny) = -[1×log₂(1) + 0×log₂(0)] = 0
加权平均熵 = (2/5)×0 + (2/5)×1.0 + (1/5)×0 = 0.4
Gain(Sunny, Temp) = 0.971 - 0.4 = 0.571c) 特征：风力Wind (在Sunny分支)
-
Weak: 3个样本（1Yes, 2No）
-
Strong: 2个样本（1Yes, 1No）
# Weak分支
P(Yes|Weak) = 1/3 ≈ 0.333, P(No|Weak) = 2/3 ≈ 0.667
Entropy(Weak|Sunny) = -[0.333×log₂(0.333) + 0.667×log₂(0.667)]
= -[0.333×(-1.585) + 0.667×(-0.585)]
= -[-0.528 - 0.390] = 0.918
# Strong分支
P(Yes|Strong) = 1/2 = 0.5, P(No|Strong) = 1/2 = 0.5
Entropy(Strong|Sunny) = -[0.5×log₂(0.5) + 0.5×log₂(0.5)] = 1.0
加权平均熵 = (3/5)×0.918 + (2/5)×1.0 = 0.951
Gain(Sunny, Wind) = 0.971 - 0.951 = 0.0204.2.3 比较并选择
Gain(Sunny, 湿度Humidity) = 0.971 ← 最大
Gain(Sunny, 温度Temp) = 0.571
Gain(Sunny, 风力Wind) = 0.020选择 湿度Humidity 作为Sunny分支的节点
4.2.4 继续递归：Sunny → 湿度Humidity 分支
分支1： 湿度Humidity = High
数据子集（3个样本）：
序号 温度 风力 Play
1 Hot Weak No
2 Hot Strong No
8 Mild Weak No-
Yes = 0, No = 3
-
判定：节点纯净（全是No）
-
创建叶子节点：Play = No
分支2： 湿度Humidity = Normal
数据子集（2个样本）：
序号 温度 风力 Play
9 Cool Weak Yes
11 Mild Strong Yes-
Yes = 2, No = 0
-
判定：节点纯净（全是Yes）
-
创建叶子节点：Play = Yes
4.3 分支：天气Outlook = Rainy
数据子集（5个样本）：
序号 温度 湿度 风力 Play
4 Mild High Weak Yes
5 Cool Normal Weak Yes
6 Cool Normal Strong No
10 Mild Normal Weak Yes
14 Mild High Strong No4.3.1 计算Rainy分支的熵
-
Yes = 3, No = 2
-
P(Yes) = 3/5 = 0.6
-
P(No) = 2/5 = 0.4
-
Entropy(S_rainy) = -[0.6×log₂(0.6) + 0.4×log₂(0.4)] = 0.971
4.3.2 计算剩余特征的信息增益
a) 特征：湿度Humidity (在Rainy分支)
-
High: 2个样本（1Yes, 1No）
-
Normal: 3个样本（2Yes, 1No）
# High分支
P(Yes|High) = 1/2 = 0.5, P(No|High) = 1/2 = 0.5
Entropy(High|Rainy) = 1.0
# Normal分支
P(Yes|Normal) = 2/3 ≈ 0.667, P(No|Normal) = 1/3 ≈ 0.333
Entropy(Normal|Rainy) = -[0.667×log₂(0.667) + 0.333×log₂(0.333)]
= 0.918
加权平均熵 = (2/5)×1.0 + (3/5)×0.918 = 0.951
Gain(Rainy, Humidity) = 0.971 - 0.951 = 0.020b) 特征：温度Temp (在Rainy分支)
-
Hot: 0个样本（不计算）
-
Mild: 3个样本（2Yes, 1No）
-
Cool: 2个样本（1Yes, 1No）
# Mild分支
P(Yes|Mild) = 2/3 ≈ 0.667, P(No|Mild) = 1/3 ≈ 0.333
Entropy(Mild|Rainy) = 0.918
# Cool分支
P(Yes|Cool) = 1/2 = 0.5, P(No|Cool) = 1/2 = 0.5
Entropy(Cool|Rainy) = 1.0
加权平均熵 = (3/5)×0.918 + (2/5)×1.0 = 0.951
Gain(Rainy, Temp) = 0.971 - 0.951 = 0.020c) 特征：风力Wind (在Rainy分支)
-
Weak: 3个样本（全部Yes）
-
Strong: 2个样本（全部No）
# Weak分支
P(Yes|Weak) = 3/3 = 1, P(No|Weak) = 0/3 = 0
Entropy(Weak|Rainy) = 0
# Strong分支
P(Yes|Strong) = 0/2 = 0, P(No|Strong) = 2/2 = 1
Entropy(Strong|Rainy) = 0
加权平均熵 = (3/5)×0 + (2/5)×0 = 0
Gain(Rainy, Wind) = 0.971 - 0 = 0.9714.3.3 比较并选择
Gain(Rainy, 风力Wind) = 0.971 ← 最大
Gain(Rainy, 湿度Humidity) = 0.020
Gain(Rainy, 温度Temp) = 0.020选择 风力Wind 作为Rainy分支的节点
4.3.4 继续递归：Rainy → 风力Wind 分支
分支1：Wind = Weak
数据子集（3个样本）：
序号 温度 湿度 Play
4 Mild High Yes
5 Cool Normal Yes
10 Mild Normal Yes-
Yes = 3, No = 0
-
判定：节点纯净（全是Yes）
-
创建叶子节点：Play = Yes
分支2：Wind = Strong
数据子集（2个样本）：
序号 温度 湿度 Play
6 Cool Normal No
14 Mild High No-
Yes = 0, No = 2
-
判定：节点纯净（全是No）
-
创建叶子节点：Play = No
第5步：所有叶子节点的判定过程汇总
| 节点路径 | 样本数 | Yes | No | 纯度 | 判定类别 | 停止原因 |
|---|---|---|---|---|---|---|
| Outlook=Overcast | 4 | 4 | 0 | 1.00 | Yes | 节点纯净 |
| Outlook=Sunny, Humidity=High | 3 | 0 | 3 | 1.00 | No | 节点纯净 |
| Outlook=Sunny, Humidity=Normal | 2 | 2 | 0 | 1.00 | Yes | 节点纯净 |
| Outlook=Rainy, Wind=Weak | 3 | 3 | 0 | 1.00 | Yes | 节点纯净 |
| Outlook=Rainy, Wind=Strong | 2 | 0 | 2 | 1.00 | No | 节点纯净 |
第6步：最终决策树的完整结构
[Outlook: Gain=0.247]
/ | \
/ | \
/ | \
Sunny Overcast Rainy
(Entropy=0.971) (纯Yes) (Entropy=0.971)
| |
[湿度Humidity: Gain=0.971] [风力Wind: Gain=0.971]
/ \ / \
湿度=高 湿度=正常 风力=弱 风力=强
(Entropy=0) (Entropy=0) (Entropy=0) (Entropy=0)
| | | |
No Yes Yes No
(3个样本) (2个样本) (3个样本) (2个样本)代码
python
import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# 设置随机种子保证可重复性
np.random.seed(42)
# 生成更丰富的数据（类似于天气预测是否打球的例子）
n_samples = 200
# 生成特征数据
weather_options = ['晴', '阴', '雨']
weather = np.random.choice(weather_options, size=n_samples, p=[0.4, 0.3, 0.3])
temp_options = ['热', '中', '冷']
temperature = np.random.choice(temp_options, size=n_samples, p=[0.4, 0.4, 0.2])
humidity_options = ['高', '正常']
humidity = np.random.choice(humidity_options, size=n_samples, p=[0.5, 0.5])
wind_options = ['强', '弱']
wind = np.random.choice(wind_options, size=n_samples, p=[0.4, 0.6])
# 基于规则生成目标变量（模拟真实决策过程）
play = []
for w, t, h, wd in zip(weather, temperature, humidity, wind):
# 设置一些决策规则
if w == '晴':
if h == '高':
play.append('否') # 晴天+湿度高 → 不打球
else:
play.append('是') # 晴天+湿度正常 → 打球
elif w == '阴':
# 阴天大多数情况打球
if t == '热' and h == '高':
play.append('否') # 阴天+热+高湿 → 不打球
else:
play.append('是')
else: # 雨天
if wd == '强':
play.append('否') # 雨天+强风 → 不打球
else:
play.append('是') # 雨天+弱风 → 打球
# 添加一些噪声（让数据更真实）
for i in range(int(n_samples * 0.1)): # 10%的噪声
idx = np.random.randint(0, n_samples)
play[idx] = '是' if play[idx] == '否' else '否'
# 创建DataFrame
df = pd.DataFrame({
'天气': weather,
'温度': temperature,
'湿度': humidity,
'风力': wind,
'打球': play
})
print("数据预览：")
print(df.head(2))
print(f"\n数据形状：{df.shape}")
print("\n数据分布：")
print(df['打球'].value_counts())
print("\n特征分布：")
for col in ['天气', '温度', '湿度', '风力']:
print(f"{col}: {df[col].value_counts().to_dict()}")
# 数据预处理
X = df[['天气', '温度', '湿度', '风力']]
y = df['打球']
# one-hot 编码
X_encoded = pd.get_dummies(X, drop_first=False)
print(f"\n编码后特征维度：{X_encoded.shape}")
print("\n编码后特征列名：")
print(X_encoded.columns.tolist())
# 训练决策树（ID3使用entropy作为标准）
clf = DecisionTreeClassifier(
criterion='entropy', # 使用信息增益（ID3的核心）
max_depth=4, # 限制树深度，避免过拟合
min_samples_split=5, # 最小分裂样本数
min_samples_leaf=2, # 叶节点最小样本数
random_state=42
)
# 训练模型
clf.fit(X_encoded, y)
# 可视化决策树
plt.figure(figsize=(16, 10))
plot_tree(clf,
feature_names=X_encoded.columns.tolist(),
class_names=['否', '是'],
filled=True,
rounded=True,
fontsize=10,
max_depth=4)
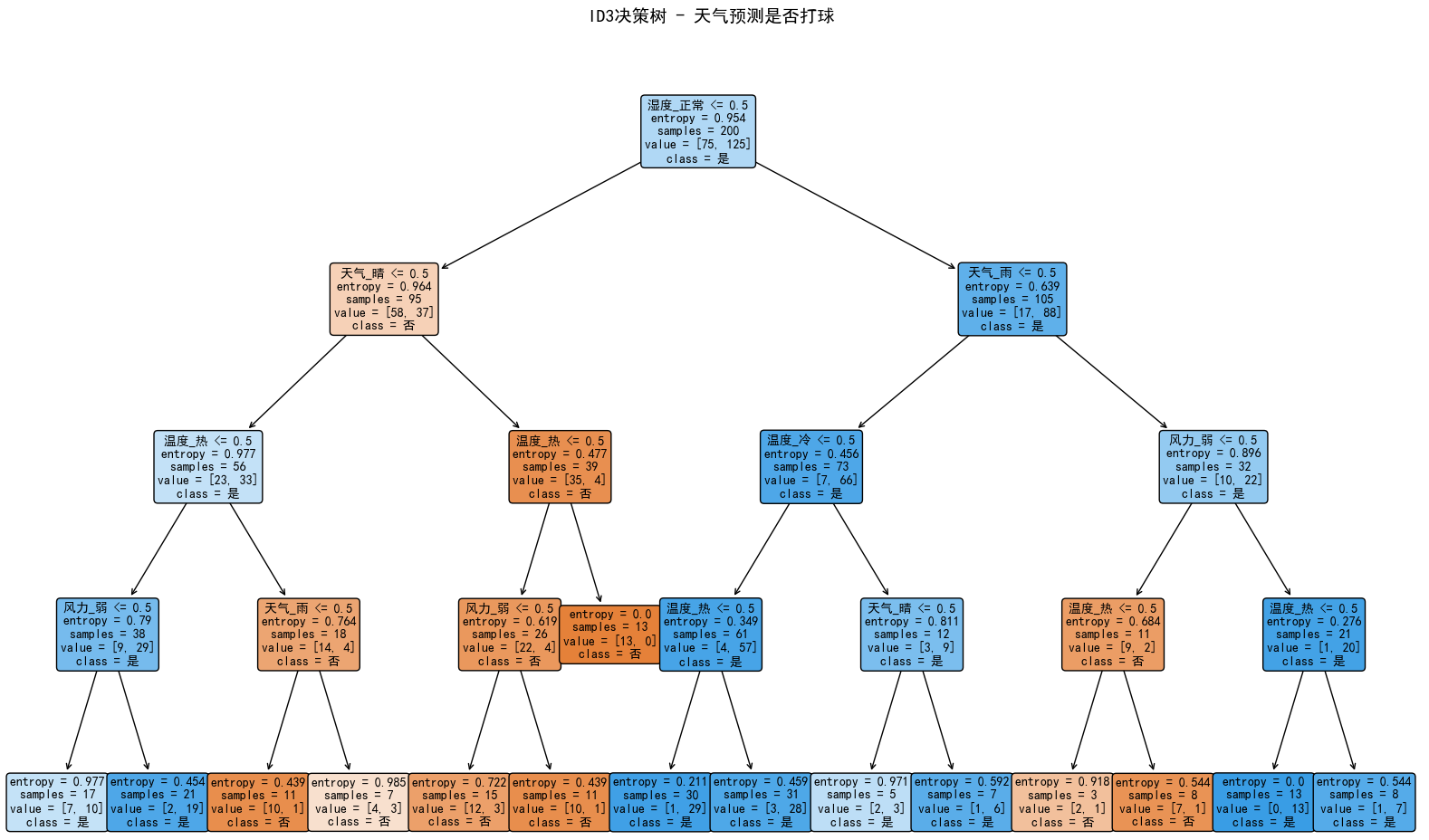
plt.title("ID3决策树 - 天气预测是否打球", fontsize=14, pad=20)
plt.tight_layout()
plt.show()
# 打印树的结构信息
print("\n=== 决策树结构信息 ===")
print(f"树深度: {clf.get_depth()}")
print(f"叶节点数: {clf.get_n_leaves()}")
print(f"特征重要性:")
for feature, importance in zip(X_encoded.columns, clf.feature_importances_):
if importance > 0:
print(f" {feature}: {importance:.3f}")
# 测试模型性能
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix
# 训练集上的预测
y_pred = clf.predict(X_encoded)
accuracy = accuracy_score(y, y_pred)
print(f"\n训练集准确率: {accuracy:.3f}")
# 生成测试数据
test_data = pd.DataFrame({
'天气': ['晴', '阴', '雨', '晴', '雨'],
'温度': ['热', '中', '冷', '中', '中'],
'湿度': ['高', '正常', '高', '正常', '正常'],
'风力': ['弱', '强', '弱', '强', '弱']
})
print("\n=== 测试预测 ===")
for i in range(len(test_data)):
# 准备测试样本
test_sample = pd.DataFrame([test_data.iloc[i]])
test_encoded = pd.get_dummies(test_sample)
# 对齐特征列
test_encoded = test_encoded.reindex(columns=X_encoded.columns, fill_value=0)
# 预测
prediction = clf.predict(test_encoded)
probability = clf.predict_proba(test_encoded)
print(f"\n样本 {i + 1}:")
print(f" 特征: {dict(test_data.iloc[i])}")
print(f" 预测: {'打球' if prediction[0] == '是' else '不打球'}")
print(f" 概率: 不打球={probability[0][0]:.2f}, 打球={probability[0][1]:.2f}")
# 创建更简单的示例来展示完整的树
print("\n=== 简单示例展示完整树结构 ===")
simple_data = {
'天气': ['晴', '晴', '阴', '雨', '雨', '雨', '阴', '晴', '晴', '雨'],
'温度': ['热', '热', '热', '中', '冷', '冷', '冷', '中', '冷', '中'],
'湿度': ['高', '高', '高', '高', '正常', '正常', '正常', '正常', '高', '正常'],
'打球': ['否', '否', '是', '是', '是', '否', '是', '否', '是', '是']
}
simple_df = pd.DataFrame(simple_data)
X_simple = simple_df[['天气', '温度', '湿度']]
y_simple = simple_df['打球']
X_simple_encoded = pd.get_dummies(X_simple)
simple_clf = DecisionTreeClassifier(criterion='entropy', max_depth=3, random_state=42)
simple_clf.fit(X_simple_encoded, y_simple)
plt.figure(figsize=(12, 8))
plot_tree(simple_clf,
feature_names=X_simple_encoded.columns.tolist(),
class_names=['否', '是'],
filled=True,
rounded=True,
fontsize=9)
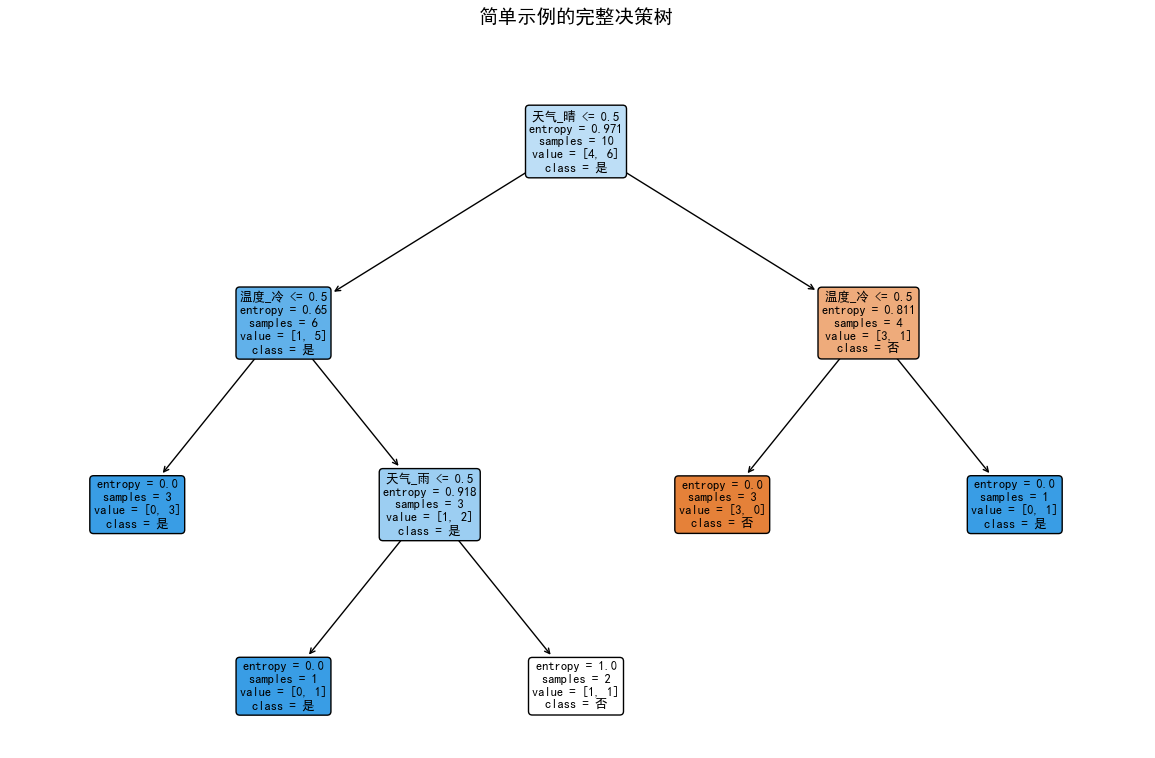
plt.title("简单示例的完整决策树", fontsize=14, pad=20)
plt.tight_layout()
plt.show()执行结果
python
数据预览：
天气 温度 湿度 风力 打球
0 晴 中 高 强 是
1 雨 热 正常 强 否
风力: {'弱': 111, '强': 89}
编码后特征维度：(200, 10)
编码后特征列名：
['天气_晴', '天气_阴', '天气_雨', '温度_中', '温度_冷', '温度_热', '湿度_正常', '湿度_高', '风力_弱', '风力_强']
=== 决策树结构信息 ===
树深度: 4
叶节点数: 15
特征重要性:
天气_晴: 0.198
天气_雨: 0.074
温度_冷: 0.023
温度_热: 0.167
湿度_正常: 0.334
风力_弱: 0.204
训练集准确率: 0.865
=== 测试预测 ===
样本 1:
特征: {'天气': '晴', '温度': '热', '湿度': '高', '风力': '弱'}
预测: 不打球
概率: 不打球=1.00, 打球=0.00
样本 2:
特征: {'天气': '阴', '温度': '中', '湿度': '正常', '风力': '强'}
预测: 打球
概率: 不打球=0.03, 打球=0.97
样本 3:
特征: {'天气': '雨', '温度': '冷', '湿度': '高', '风力': '弱'}
预测: 打球
概率: 不打球=0.10, 打球=0.90
样本 4:
特征: {'天气': '晴', '温度': '中', '湿度': '正常', '风力': '强'}
预测: 打球
概率: 不打球=0.03, 打球=0.97
样本 5:
特征: {'天气': '雨', '温度': '中', '湿度': '正常', '风力': '弱'}
预测: 打球
概率: 不打球=0.00, 打球=1.00
=== 简单示例展示完整树结构 ===
