目录
[1.1.Automatically Select (自动选择模式)](#1.1.Automatically Select (自动选择模式))
[1.2. Pipelined, Streaming I/O (流水线流式模式)](#1.2. Pipelined, Streaming I/O (流水线流式模式))
[1.3. Radix-4, Burst I/O (基4 突发模式)](#1.3. Radix-4, Burst I/O (基4 突发模式))
[1.4. Radix-2 / Radix-2 Lite, Burst I/O (基2 极简模式)](#1.4. Radix-2 / Radix-2 Lite, Burst I/O (基2 极简模式))
[1.6.2. 舍入模式 (Rounding Modes)](#1.6.2. 舍入模式 (Rounding Modes))
[Convergent Rounding(收敛舍入):硬件上的"计算器"](#Convergent Rounding(收敛舍入):硬件上的“计算器”)
[1.6.3. 数据与相位位宽 (Bit Width)](#1.6.3. 数据与相位位宽 (Bit Width))
[1.6.4. 窗函数与能量泄漏 (Windowing)](#1.6.4. 窗函数与能量泄漏 (Windowing))
[2.STFT 在FPGA中实现的原理](#2.STFT 在FPGA中实现的原理)
[3.1时间同步的问题:硬复位对齐 vs. 连续打标模式](#3.1时间同步的问题:硬复位对齐 vs. 连续打标模式)
[方案一:硬复位模式(Hard Reset Mode)------ 追求绝对对齐](#方案一:硬复位模式(Hard Reset Mode)—— 追求绝对对齐)
[方案二:连续打标模式(Continuous Tagging Mode)------ 追求物理连续性](#方案二:连续打标模式(Continuous Tagging Mode)—— 追求物理连续性)
前言
此笔记主要是为了记录在测试STFT代码时遇到的问题和测试的方法。
1.FFT的模式
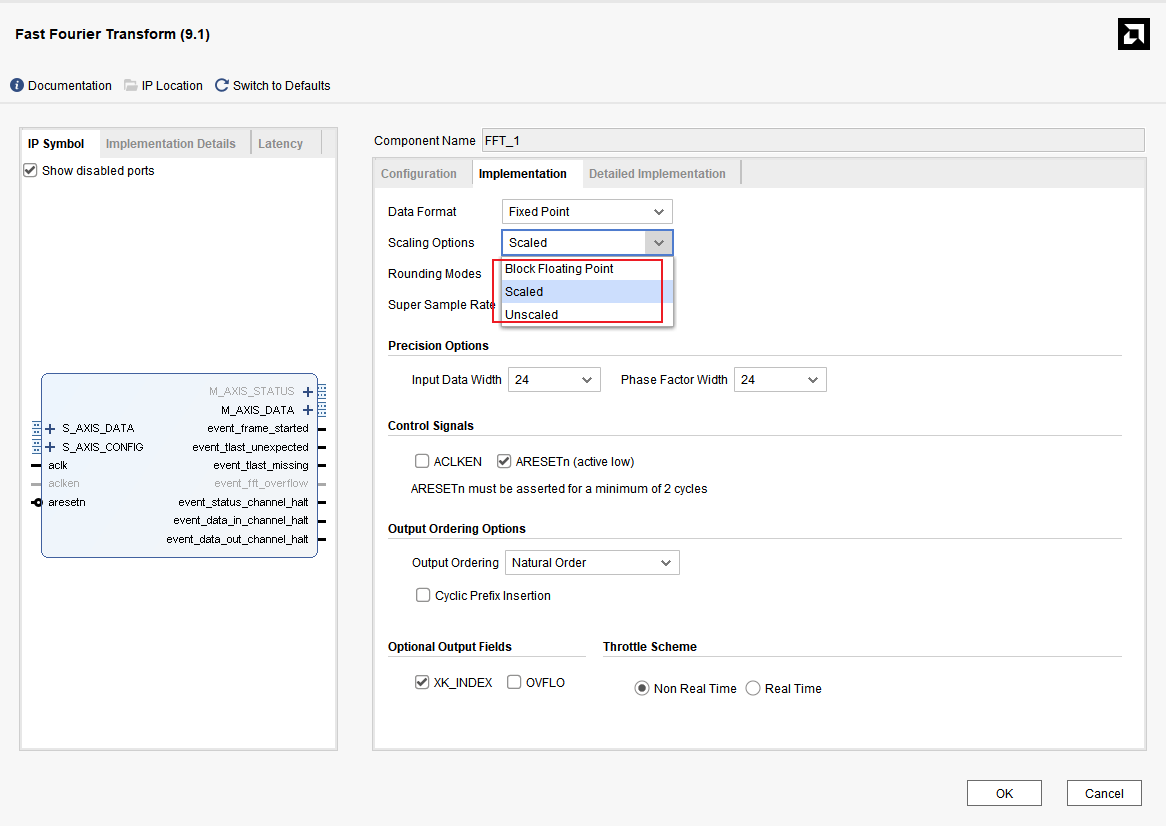
先回顾一下FFT的四种模式,如下图FFT IP核的配置界面所示。
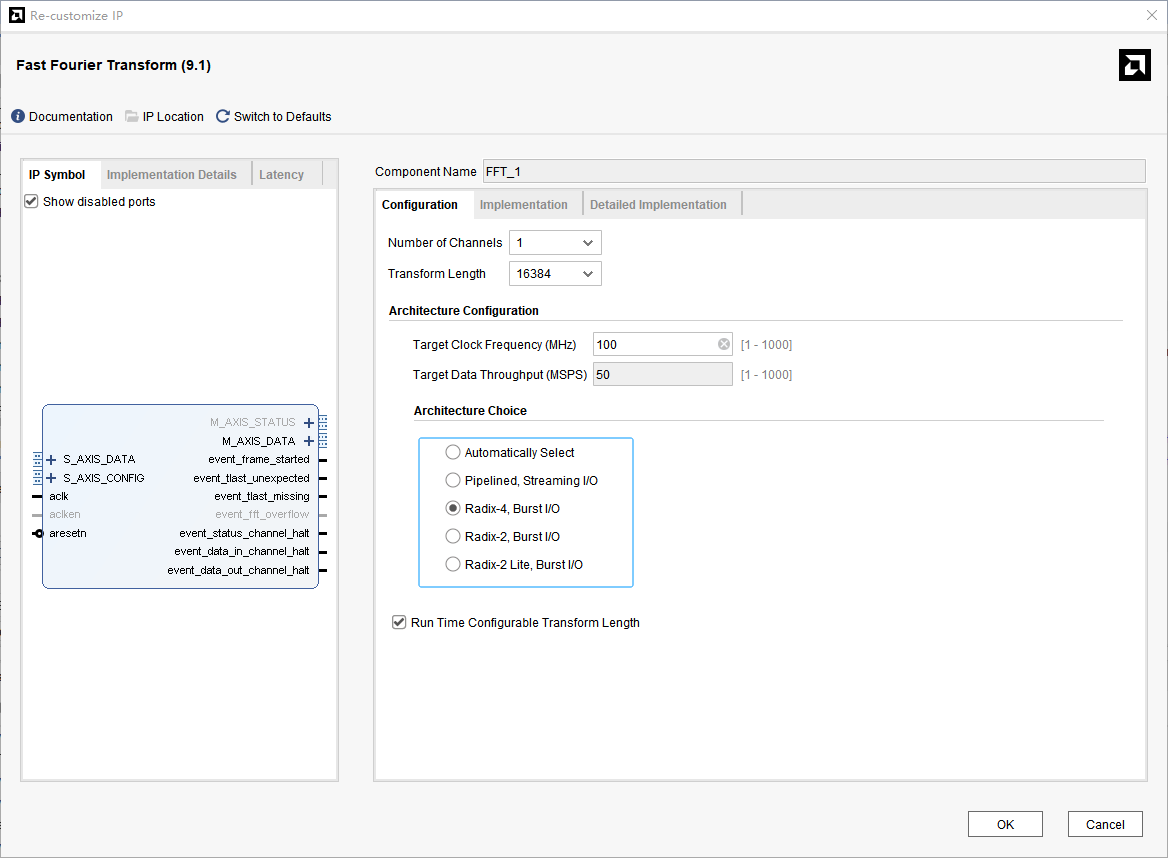
图中,Architecture Choice (架构选择)目前勾选的是 Automatically Select (自动选择)。 Vivado 会根据设定的 Target Data Throughput (50 MSPS) 和 Target Clock Frequency (100 MHz) 自动挑选最合适的实现方式。
Xilinx Fast Fourier Transform (FFT) IP 核的架构有以下几种:
1.1.Automatically Select (自动选择模式)
这是最省心但也最容易"失控"的模式。
- 特点 :其核心逻辑是基于你设定的目标吞吐量 (50MSPS}) 与时钟频率 (100 MHz) 的比例,在后台通过启发式算法自动匹配硬件架构。它试图在不干预细节的前提下,自动寻找能满足实时性要求的平衡点。
- 资源消耗 :具有极强的不确定性。在变换长度较小时,它能很好地节省资源;但当长度达到 16384$ 这种极限值时,它往往会为了绝对保证 50MSPS 的指标而"保险起见",盲目锁定在最昂贵的流水线架构上,导致 Block RAM (BRAM) 消耗失控。
1.2. Pipelined, Streaming I/O (流水线流式模式)
这是性能最强但也最"贪婪"的模式。
-
特点:可以连续不断地输入和输出数据,中间没有停顿。
-
资源消耗 :由于需要大量的中间缓存来实现流水线操作,它消耗的 Block RAM (BRAM) 和 DSP 资源最多。
-
图中选择 :由于图中的 Transform Length (变换长度) 设为了 16384 ,且吞吐量要求较高,Vivado 极大概率自动选了这个模式。这就是导致你 BRAM 需求达到 1059 个、远超芯片上限 890 个的主因。
1.3. Radix-4, Burst I/O (基4 突发模式)
-
特点:数据采用"加载---处理---卸载"的周期性方式。处理时不能输入新数据。
-
资源消耗:比流式模式节省大量资源。
-
建议:如果能接受非连续的 STFT 处理(或者通过外部更简单的逻辑做缓冲),切换到这个模式可以大幅缓解资源压力。
1.4. Radix-2 / Radix-2 Lite, Burst I/O (基2 极简模式)
-
特点:结构最简单。
-
资源消耗:消耗 BRAM 最少。
-
缺点:处理速度最慢。
1.5.资源消耗和精度对比
| 模式名称 | 数据吞吐特性 | 资源消耗 (BRAM/DSP) | 适用场景 |
|---|---|---|---|
| Pipelined, Streaming I/O | 持续流式:允许在输出上一帧的同时输入当前帧,无间断。 | 最高:为了维持流水线,需要大量的中间缓存。 | 高带宽实时系统(如你的 50 MSPS 直采)。 |
| Radix-4, Burst I/O | 分批突发:采用"加载-处理-卸载"三步走,处理期间不能输入新数据。 | 显著降低:由于不需要全时流水线,BRAM 消耗大幅减少。 | 资源受限(如你的 K7-325T 情况)且允许非连续处理的系统。 |
| Radix-2, Burst I/O | 低速突发:逻辑最简单,单时钟周期处理能力较低。 | 更低:进一步节省面积。 | 对实时性要求极低、资源极度匮乏的场景。 |
| Radix-2 Lite, Burst I/O | 极简突发:牺牲速度换取最小面积。 | 最低:最小的 BRAM 占用。 | 仅需偶尔计算 FFT 的控制类应用。 |
| 模式 | 数学计算精度 | 量化噪声 (SQNR) | 你的系统表现 (精度损失) |
|---|---|---|---|
| Pipelined, Streaming I/O | 最高:每级流水线有独立硬件,通常采用全精度位宽扩展。 | 理论最优。 | 极差:因 Hold 违例 产生的随机误码和丢包,导致数据有效位数(ENOB)剧降。 |
| Radix-4, Burst I/O | 中等偏上:通过多次迭代复用逻辑,舍入误差可能因循环微量累积。 | 与流式模式基本持平。 | 稳定:由于资源占用率低,时序容易收敛,能够完整保持 24-bit 信号的动态范围。 |
| Radix-2 / Lite | 标准:计算路径最长,级数更多。 | 舍入噪声理论上略高于基-4。 | 冗余:对于 50 MSPS 任务,处理延迟可能导致实时性精度损失。 |
1.6.影响精度的因素
对于 Xilinx FFT IP 核(v9.1)及 STFT 逻辑,影响计算精度的设置主要有以下维度:
1.6.1缩放模式与缩放系数 (Scaling)
这是固定点 FFT 精度最大的"杀手"。由于 FFT 每一级计算都会导致位宽增长,为了防止溢出,必须进行缩放。
缩放方案选择:
Unscaled:不缩放,精度最高,但极易导致结果溢出(变为无效数据)。
Scaled :通过
SCALE_SCH手动控制每一级的移位。你当前设置的16'haaaa表示每级右移 2 bit。Block Floating Point:由硬件自动根据数据大小缩放,能提供最大的动态范围。
(对缩放因子的理解FPGA FFT缩放因子配置全解析-CSDN博客)
- 精度影响:过于保守的缩放(如全 2)会丢弃低位数据,导致信噪比(SNR)下降;缩放不足则会导致严重的溢出畸变。
1.6.2. 舍入模式 (Rounding Modes)
在数据位宽截断时,如何处理被丢弃的低位。
Truncation(截断):硬件上的"剪刀"
直接扔掉低位。虽然节省逻辑资源,但会引入明显的直流偏置误差(Bias)。
实现原理 :在 FPGA 内部,截断仅仅是一个"总线选择"操作。比如将 34 位数据截断为 24 位,在 Verilog 中只是
assign out = in[33:10]。资源代价:这种操作不占用任何 LUT 或 DSP 资源,它只是改变了信号的布线连接。
Convergent Rounding(收敛舍入):硬件上的"计算器"
类似于"四舍五入到偶数"。它能显著降低量化噪声,提高无杂散动态范围(SFDR),是科学级载荷的首选配置。
实现原理:收敛舍入(Round to Nearest Even)需要对被截断的低位进行逻辑判断。
如果低位 > 0.5,则高位加 1。
如果低位 < 0.5,则直接截断。
如果低位恰好等于 0.5,则根据高位的奇偶性决定是否进位。
资源代价:
加法器链:为了实现"+1"操作,FFT IP 核必须在每一级蝶形运算后增加一组加法器。
逻辑开销 :由于你的 FFT 变换长度高达 16384,这种加法器逻辑会成倍增加,直接推高 LUT 的使用率。
维度 Truncation (截断) Convergent Rounding (收敛舍入) 逻辑资源 (LUT) 极低(几乎为零) 较高:每一级蝶形运算后都需要额外的加法器逻辑。 寄存器 (FF) 无额外消耗 增加:通常需要增加流水线级数以补偿舍入逻辑带来的延迟。 时序影响 无:仅为连线关系。 显著 :增加了逻辑层级,可能恶化现有的 Hold 违例。 实现难度 简单:直接选取高位。 复杂:需判断舍入位、余数位及结果的奇偶性。
1.6.3. 数据与相位位宽 (Bit Width)
- 输入位宽 :目前使用的是 24-bit 。这是极高的精度,能够覆盖约
的理论动态范围。
相位位宽 (Phase Factor Width):旋转因子的精度。如果旋转因子位宽(通常设为 16-24 bit)不足,会在频谱中产生伪峰(Spurs)。
中间结果位宽:IP 核内部累加器的位宽。如果为了节省 BRAM 而限制了中间位宽,精度会迅速劣化。
1.6.4. 窗函数与能量泄漏 (Windowing)
这是 STFT 算法层面的精度影响。
扇贝损失 (Scalloping Loss):如果没有使用窗函数,信号频率如果不落在频点中心,幅值测量会偏小。
频谱泄漏:矩形窗泄漏严重,会将大信号的能量扩散到相邻频点,淹没附近的小信号。
解决方法 :在
STFT.v中加入汉宁窗(Hanning)或海明窗(Hamming)进行加窗处理。目前的代码里面使用的是汉宁窗。
2.STFT 在FPGA中实现的原理
2.1主要的逻辑框架
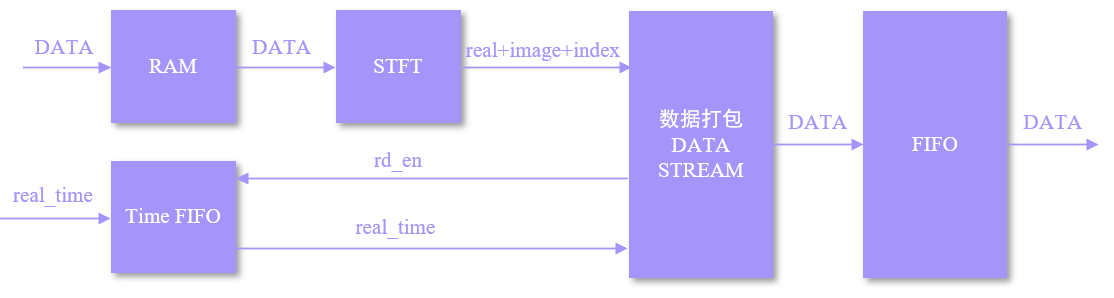
核心逻辑如下:
- 缓冲区指针控制逻辑
模块基于RAM 构建同步循环缓冲区,通过双指针机制管理数据流。写指针实时跟踪采样数据的存入地址;读指针则定位当前处理帧的起始位置。每完成单帧( 点)数据的读取,读指针按预设步进(Hop Size)进行偏移,从而精确控制 STFT 的时间重叠率。
-
读写触发策略
-
写入逻辑:受采样有效信号门控,仅在数据有效周期执行写操作。
-
读取逻辑 :当缓冲区内累积的样点数达到
(如 1024 点)时,触发读使能,将数据突发(Burst)供入 FFT IP 核。
-
-
时间戳同步机制 (Time_FIFO)
系统会将每一帧的第一个数据的采样时间戳压入 Time_FIFO。当 STFT 变换完成且输出有效信号(vaild)拉高时,同步从 FIFO 中弹出对应帧的起始时刻,当这一帧的数据读取完之后等到下一次输出信号拉高才会读取时间。一次运算结果分帧打包时还是按格式打包,只是每一帧的结束之后不直接返回S_IDLE,而是从S_START开始,直到打包完这一次运算结果。
以上就是主要的实现逻辑。
2.2测试代码
Matlab
%% STFT 数据解析 (针对布局:Imag[0-2], Real[3-5], Idx[6-7])
clc,clear,close all
path0 = 'D:\FPGA\pro\FPGA_RTL\C++\data\20260124\';
path = path0;
%2026-01-24
file1 = [path,'STFT_CH1-CH123-T2.34s-20260124-174100-036.dat']; %10Hz~2MHz方波扫频信号,1s扫频周期 模拟数据
file2 = [path,'STFT_CH2-CH123-T2.34s-20260124-174100-036.dat']; %10Hz~2MHz方波扫频信号,1s扫频周期 模拟数据
file4 = [path,'STFT_CH1-CH1-T2.34s-20260124-201524-147.dat']; %10Hz~250kHz正弦波扫频信号,1s扫频周期 模拟数据
file5 = [path,'STFT_CH1-CH1-T2.34s-20260124-212112-948.dat']; %10Hz~250kHz正弦波扫频信号,1s扫频周期 模拟数据
filename = file1;
% --- 1. 核心参数配置 ---
T = 0.234; % 读取时长 (秒)
fs_stft = 250e3; % 抽样后频率
N_fft = 1024; % FFT 计算点数
noverlap = 512; % 重叠 512
N_bins_one_sided = 513; % 单边谱点数 (1024/2 + 1)
% 步进时间计算
time_step = (N_fft - noverlap) / fs_stft; % 2.048ms
% --- 2. 读取二进制文件 ---
N = T * fs_stft*2*8;
fid = fopen(filename, 'rb');
if fid == -1, error('文件打开失败!'); end
raw_bytes = fread(fid, N, 'uint8');
fclose(fid);
% 每一项 8 字节 (64-bit)
num_samples = floor(length(raw_bytes) / 8);
data_matrix = reshape(raw_bytes(1:num_samples*8), 8, []);
% --- 3. 严格按照位域解析 (Idx[6-7], Real[3-5], Imag[0-2]) ---
% 解析频率下标 (Byte 7为高位)
indices = double(data_matrix(8,:)) * 256 + double(data_matrix(7,:));
% 解析实部与虚部 (24-bit 补码处理)
real_raw = double(data_matrix(6,:)) * 65536 + double(data_matrix(5,:)) * 256 + double(data_matrix(4,:));
real_raw(real_raw >= 2^23) = real_raw(real_raw >= 2^23) - 2^24;
imag_raw = double(data_matrix(3,:)) * 65536 + double(data_matrix(2,:)) * 256 + double(data_matrix(1,:));
imag_raw(imag_raw >= 2^23) = imag_raw(imag_raw >= 2^23) - 2^24;
% 计算幅值
magnitude = abs(real_raw + 1i * imag_raw);
% --- 3. 矩阵重构 (仅提取前 513 个频点) ---
frame_start_pos = find(indices == 0);
% 只保留后面跟着 1 的那个 0 才是真实的帧起始
frame_start_pos = frame_start_pos(indices(frame_start_pos + 1) == 1);
total_len = length(magnitude);
num_frames_raw = length(frame_start_pos);
spec_matrix = [];
valid_frame_cnt = 0;
for n = 1 : num_frames_raw
curr_start = frame_start_pos(n);
% 检查数据是否足以支撑提取到第 512 号下标 (共 513 个点)
if (curr_start + N_bins_one_sided - 1) <= total_len
valid_frame_cnt = valid_frame_cnt + 1;
% 【关键修正】:只截取 [0, 512] 的下标
spec_matrix(:, valid_frame_cnt) = magnitude(curr_start : curr_start + N_bins_one_sided - 1);
end
end
% --- 4. 坐标轴生成 ---
% 频率轴: 0 ~ 125kHz (513 个点)
f_axis = (0 : N_bins_one_sided - 1) * (fs_stft / N_fft) / 1000;
% 时间轴
t_axis = (0 : valid_frame_cnt - 1) * time_step;
% --- 5. 可视化 ---
figure('Color', 'w');
% 绘制单边谱,通常在 dB 下观察
imagesc(t_axis, f_axis, 20*log10(spec_matrix + 1e-6));
C_Limit = [40 110];
y_Limit = [0 130] ;
axis xy;
colormap(jet);
clim(C_Limit);
ylim(y_Limit);
colorbar;
ylabel('频率 (kHz)'); xlabel('时间 (s)');
title('STFT 单边频谱图 ([0, fs/2] 模式)');
fprintf('解析完成:\n');
fprintf('单边谱点数: %d 点\n', N_bins_one_sided);
fprintf('最高观察频率: %.2f kHz (Nyquist)\n', f_axis(end));2.3测试结果
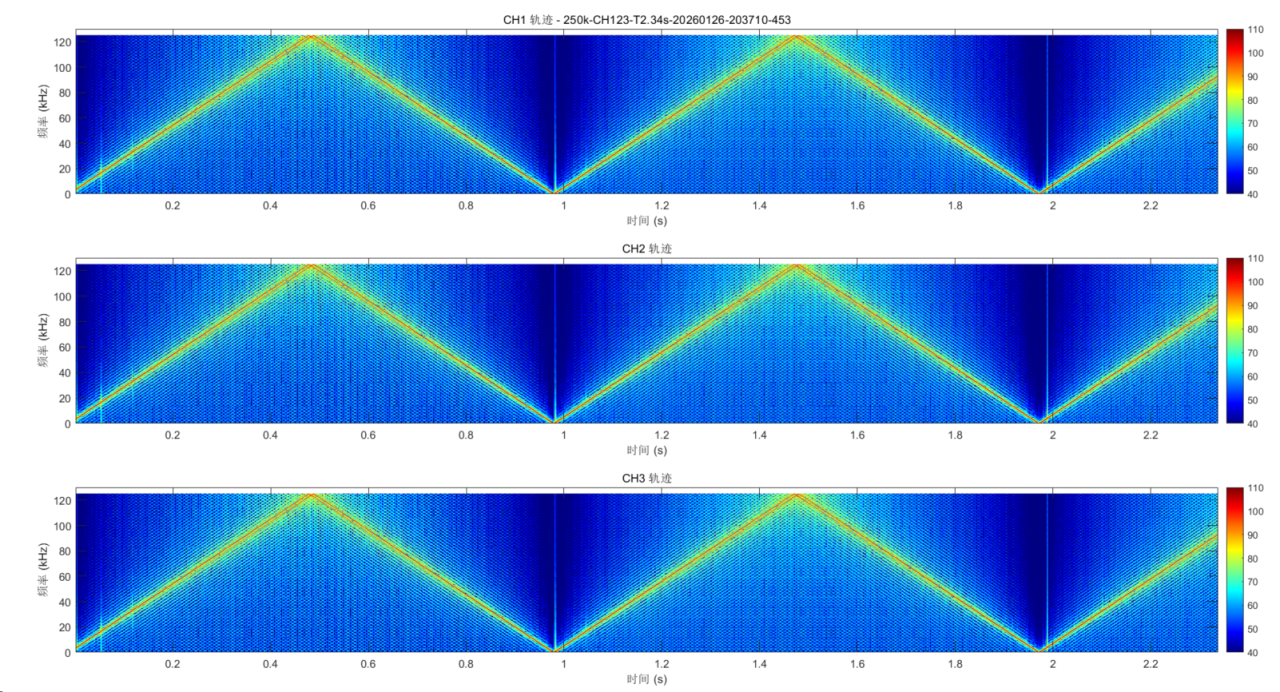
2.3.1时频图结果
STFT结果的时频图:
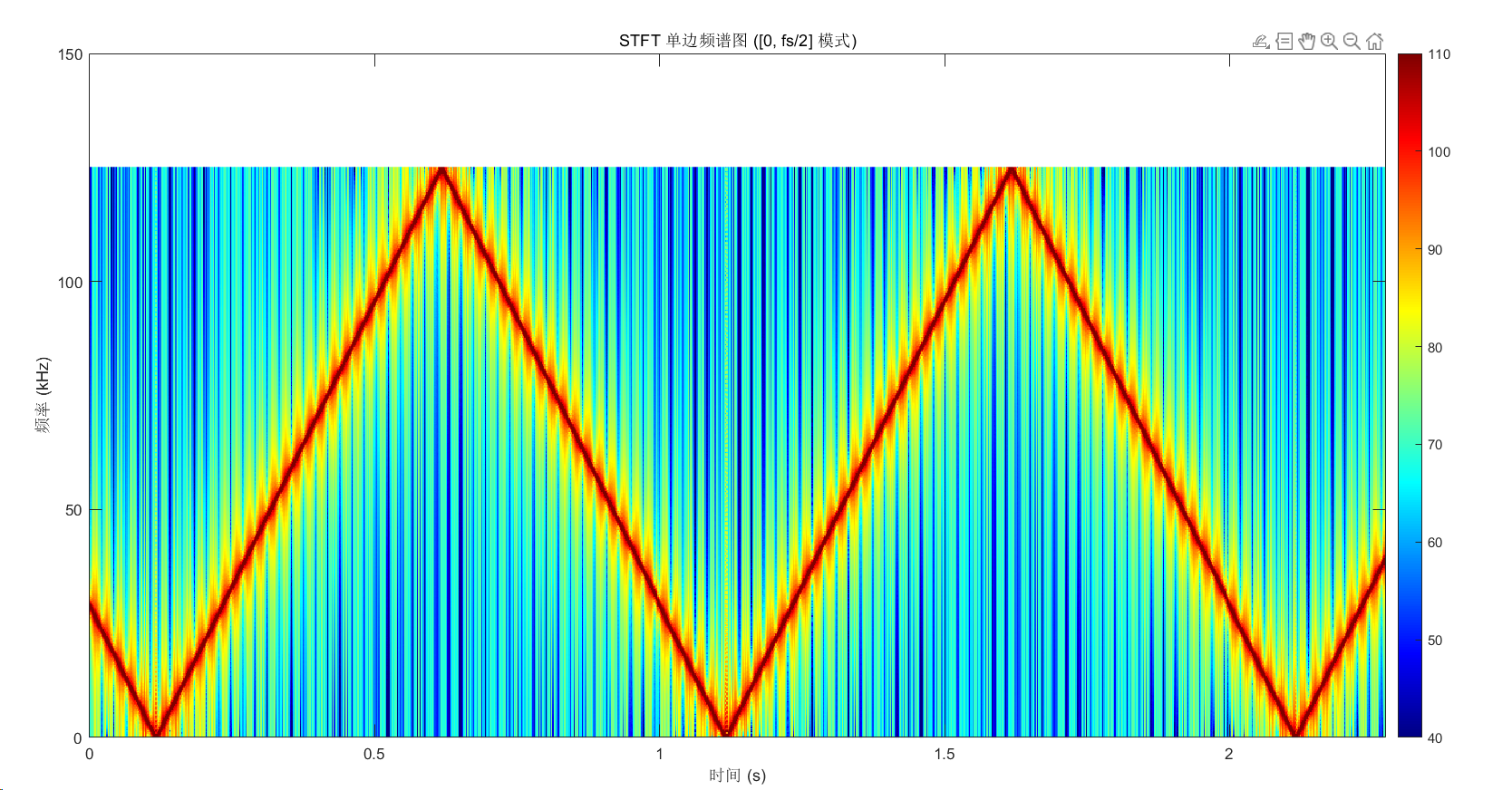
相同扫频信号数据matlab计算的结果:
2026-01-26-lhw:这个扫频信号是100hz~2Mhz的。
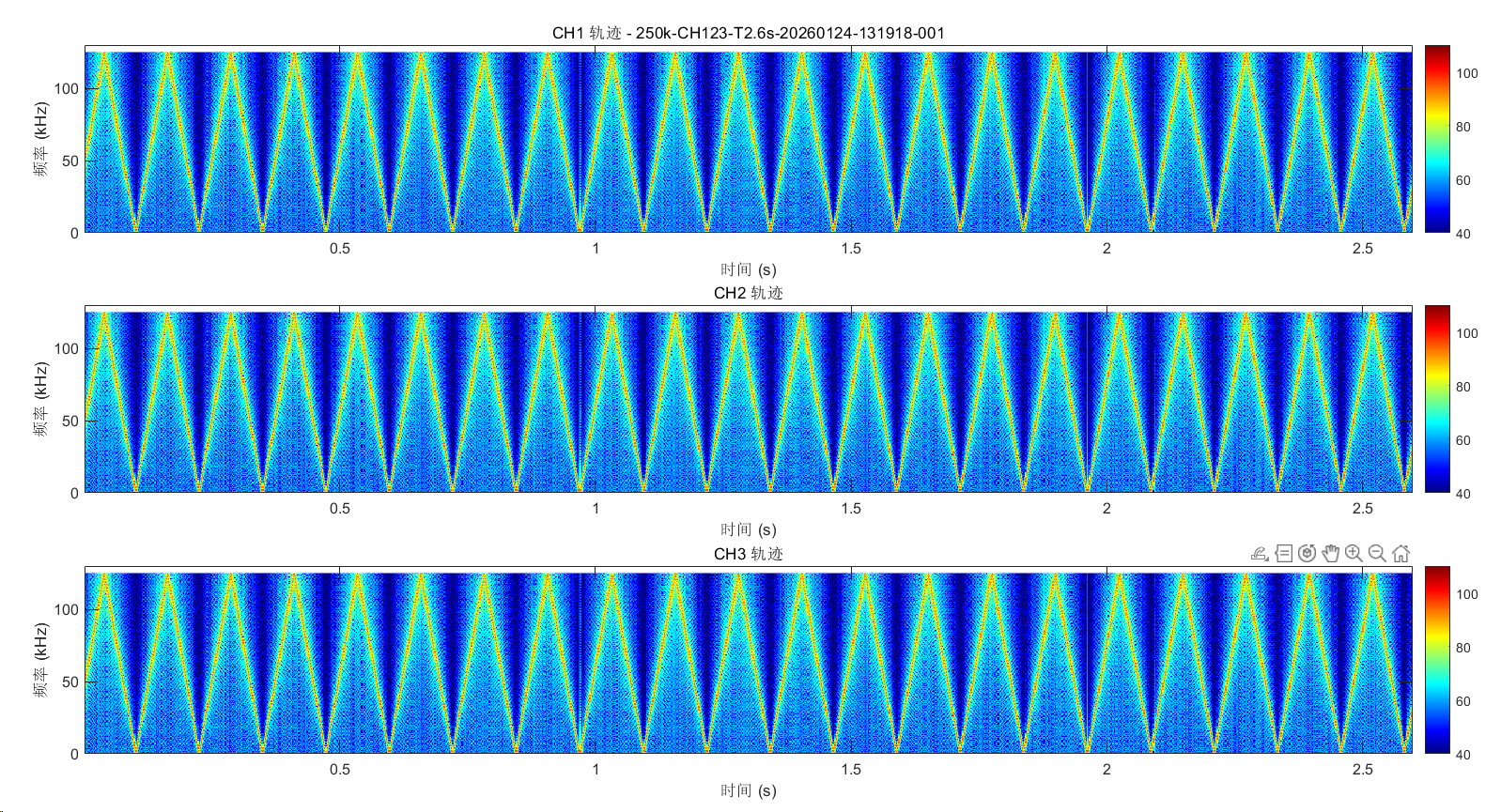
通过对比分析可见,FPGA 计算的主频能量轨迹与matlab计算结果基本吻合,但在主频点上方区域观测到非预期的能量分布。理论上,该高频区域能量应趋近于背景噪声水平,当前的异常抬升可能源于算法截断误差或硬件实现中的频谱泄漏。目前故障诱因尚不明确,后续计划利用 Vivado ILA(在线逻辑分析仪)抓取 STFT 模块各级的逐帧输出数据,进行算法验证与底层排查。
AI给出的几点可能的原因:
**为什么 MATLAB 的结果和你画的代码有区别?**之前提到"MATLAB 在线上方的频点能量几乎没有,而你的代码下方能量更小",这主要涉及以下三个底层差异:
① 归一化定义不同 (Scaling)
MATLAB :
spectrogram默认输出的是功率谱密度(PSD)或能量,它会自动除以窗函数的能量和采样频率。你的 FPGA 代码 :你直接使用了
abs(real + i*imag),并且由于硬件设置了16'haaaa,结果被缩小了 1024 倍。结果:即使信号相同,两者的绝对数值(dB 值)会相差非常大。
② 窗函数的影响 (Windowing)
MATLAB :如果你只传
window_size(标量),MATLAB 默认使用 Hamming 窗。窗函数会抑制侧瓣,使信号线看起来更"干净"。你的 FPGA 代码:如果硬件里没有加窗逻辑(矩形窗),频谱泄漏会很严重,导致信号线看起来很粗,背景杂散多。
如何实现"完全对齐"的对比?
如果你想让 MATLAB 的每一帧结果和你 FPGA 解析的
spec_matrix具有可比性,建议这样调用:
% 使用矩形窗 (rectwin) 且不进行内部归一化,以模拟 FPGA 的原始计算 [s, f, t] = spectrogram(data1, rectwin(window_size), overlap, nfft, fs); % 补偿 FPGA 的硬件缩放 (10 bit = 1024倍) fpga_frame_1 = spec_matrix(:, 1) * 1024; matlab_frame_1 = abs(s(:, 1)); % 绘图对比第一帧 plot(f, 20*log10(matlab_frame_1), 'r', 'DisplayName', 'MATLAB'); hold on; plot(f_axis, 20*log10(fpga_frame_1), 'b--', 'DisplayName', 'FPGA');
2026-01-26-lhw:具体原因分析
添加查看每一帧结果的功能:
Matlab
% ================= 动图与保存配置 =================
is_animate = true; % 动画播放开关:true 播放,false 跳过
save_gif = true; % GIF 保存开关:true 保存,false 不保存
[~, name, ~] = fileparts(filename);
gif_name = ['STFT_Frame_Animation_', name, '.gif'];
% ================= 绘图与动图逻辑 =================
if is_animate
figure('Color', 'w');
t_s = 1:1:size(spec_matrix, 1);
% 初始化第一帧
hLine = plot(t_s, spec_matrix(:, 1), 'LineWidth', 1.2, 'Color', [0 0.447 0.741]);
grid on;
xlabel('频率轴点数 (Bin Index)');
ylabel('幅值 (Magnitude)');
% 固定坐标轴,防止动图因缩放产生的视觉干扰
ylim([0, max(spec_matrix(:)) * 1.1]);
pause_time = 0.05;
num_frames = size(spec_matrix, 2);
for k = 1:num_frames
% 更新 Y 轴数据为第 k 帧
%set(hLine, 'YData', spec_matrix(:, k));
hLine.YData = spec_matrix(:, k); %两个语句是等价的
% 实时更新标题,帮助观察"虚假零帧"的能量回归过程
title(sprintf('STFT 逐帧监测 | 帧数: %d/%d | 时间: %.3f s', k, num_frames, (k-1)*time_step));
drawnow; % 强制刷新硬件绘图
% --- GIF 保存逻辑 ---
if save_gif
frame = getframe(gcf); % 获取当前窗口画面
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if k == 1
% 第一帧创建文件
imwrite(imind, cm, gif_name, 'gif', 'Loopcount', inf, 'DelayTime', pause_time);
else
% 后续帧追加到文件末尾
imwrite(imind, cm, gif_name, 'gif', 'WriteMode', 'append', 'DelayTime', pause_time);
end
end
pause(pause_time);
end
if save_gif
fprintf('GIF 动图已保存至: %s\n', gif_name);
end
else
fprintf('动画展示已关闭。如需观察每一帧能量变化,请将 is_animate 设为 true。\n');
endFPGA的STFT解算结果动态显示如下:
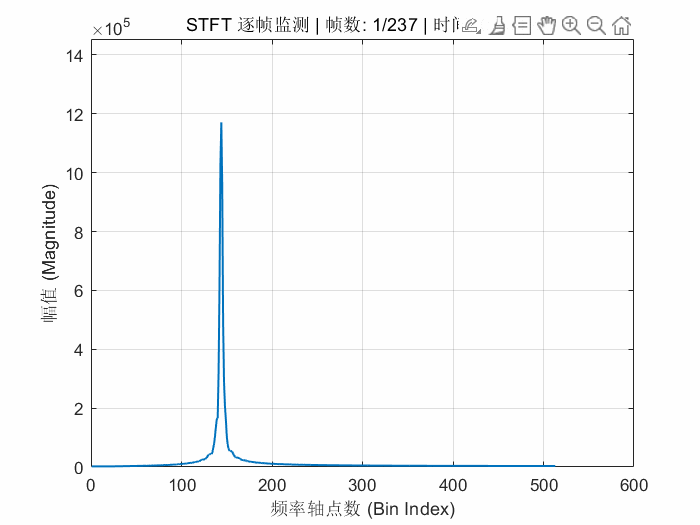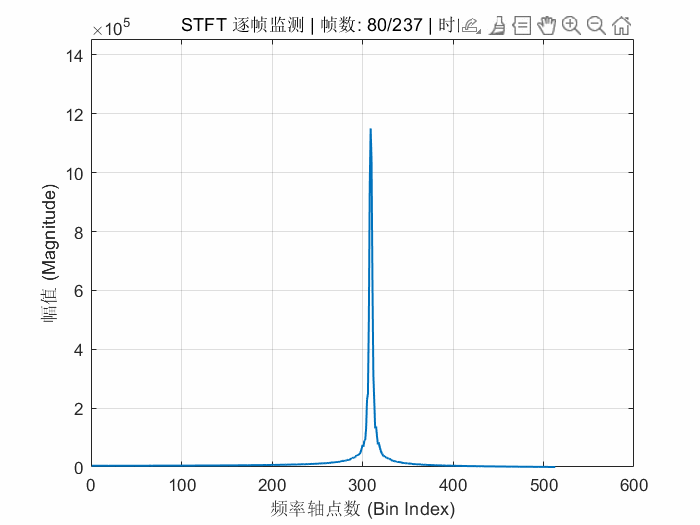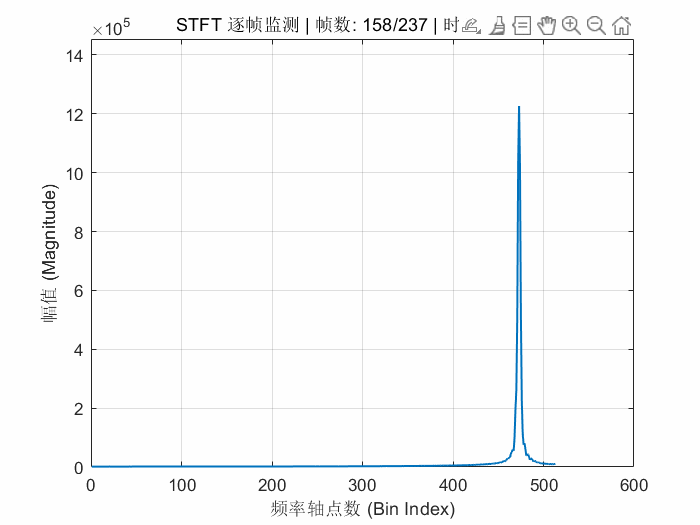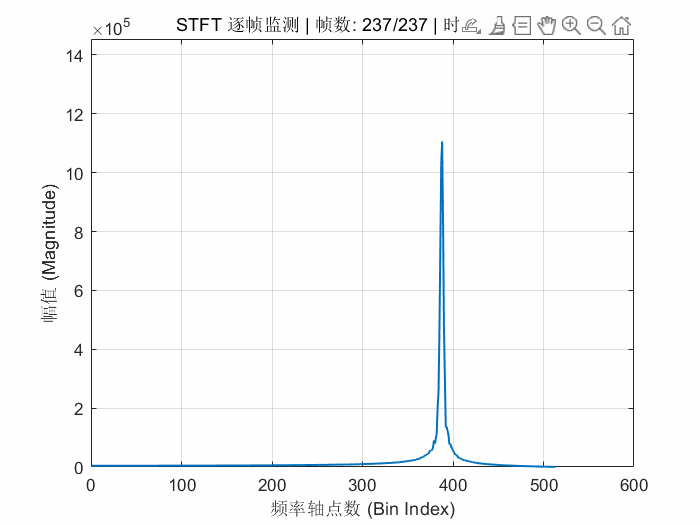
我感觉就应该像这样子对称的才是对的。
MATLAB的STFT解算结果动态显示如下:
这可能是因为用250khz采样率采集100hz~1Mhz采样率导致的。
之后用模拟的数据进行仿真:
Matlab
%2026-01-26-lhw
%% 理想扫频信号 STFT 仿真 (纯 MATLAB 浮点处理)
clc, clear, close all
% --- 1. 核心参数配置 (与工程对齐) ---
fs = 250e3; % 采样率 [cite: 2026-01-26]
T_total = 2.34; % 总时长 [cite: 2026-01-26]
N_fft = 1024; % FFT 点数
noverlap = 512; % 重叠点数
N_bins_one_sided = 513; % 单边谱点数 (N/2 + 1)
% 步进时间计算 (2.048ms)
time_step = (N_fft - noverlap) / fs;
% --- 2. 模拟信号合成 ---
t = 0:1/fs:T_total-(1/fs);
% 10Hz ~ 250kHz 正弦扫频,1s 扫频周期
% 注意:在 fs=250k 时,超过 125kHz 会发生奈奎斯特频率混叠
sweep_signal = chirp(t, 10, 1.0, 250e3, 'linear');
%% --- 3. spectrogram运算结果 ---
y_Limit = [0 130] ;
figure('Name', '时频轨迹分析', 'Color', 'w');
spectrogram(sweep_signal, N_fft, noverlap, N_fft, fs, 'yaxis');
title('时频轨迹(spectrogram)'); ylim(y_Limit); colorbar;
%%
% --- 4. 执行 STFT 计算 (手动分帧模拟) ---
hop = N_fft - noverlap;
num_frames = floor((length(sweep_signal) - N_fft) / hop) + 1;
spec_matrix = zeros(N_bins_one_sided, num_frames);
for n = 1:num_frames
idx_start = (n-1)*hop + 1;
% 提取当前帧窗口数据
frame_data = sweep_signal(idx_start : idx_start + N_fft - 1);
% 使用汉宁窗减少频谱泄漏 (模拟标准处理)
% 若想完全模拟你之前的 FPGA 矩形窗效果,可将 hanning 替换为 rectwin
win_data = frame_data .* rectwin(N_fft)';
% FFT 计算 (浮点,无缩放)
X = fft(win_data, N_fft);
% 提取单边谱幅值
spec_matrix(:, n) = abs(X(1:N_bins_one_sided));
end
% --- 4. 坐标轴定义 ---
f_axis = (0 : N_bins_one_sided - 1) * (fs / N_fft) / 1000; % kHz
t_axis = (0 : num_frames - 1) * time_step; % s
% --- 5. 静态谱图可视化 ---
figure('Color', 'w');
imagesc(t_axis, f_axis, 20*log10(spec_matrix + 1e-6));
axis xy;
colormap(jet);
C_Limit = [-30 60];
% y_Limit = [0 130] ;
clim(C_Limit);
% ylim(y_Limit);
colorbar;
ylabel('频率 (kHz)'); xlabel('时间 (s)');
title('理想扫频信号 STFT 仿真 (浮点模式)');
%% ================= 6. 进阶功能:动图展示与保存 =================
is_animate = true; % 动画播放开关
save_gif = true; % GIF 保存开关
gif_name = 'Ideal_Sweep_STFT_Animation.gif';
if is_animate
fig_anim = figure('Color', 'w', 'Name', '逐帧动态监测 (理想模拟)');
t_bin = 1:N_bins_one_sided;
% 初始化第一帧
hLine = plot(t_bin, spec_matrix(:, 1), 'LineWidth', 1.2, 'Color', [0.85, 0.33, 0.09]);
grid on;
% 由于是浮点运算,幅值上限会比定点版大得多,这里自动适应最大值
ylim([0, max(spec_matrix(:)) * 1.1]);
xlabel('频点下标 (Bin Index)'); ylabel('幅值 (浮点绝对值)');
pause_time = 0.03;
for k = 1:num_frames
if ~ishandle(fig_anim), break; end
hLine.YData = spec_matrix(:, k);
title(sprintf('仿真监测 | 帧数: %d/%d | 时间: %.3f s', k, num_frames, t_axis(k)));
drawnow;
if save_gif
frame = getframe(fig_anim);
im = frame2im(frame);
[imind, cm] = rgb2ind(im, 256);
if k == 1
imwrite(imind, cm, gif_name, 'gif', 'Loopcount', inf, 'DelayTime', pause_time);
else
imwrite(imind, cm, gif_name, 'gif', 'WriteMode', 'append', 'DelayTime', pause_time);
end
end
pause(pause_time);
end
if save_gif
fprintf('仿真动图已保存至: %s\n', gif_name);
end
end部分数据的动图:
用spectrogram计算的时频图:
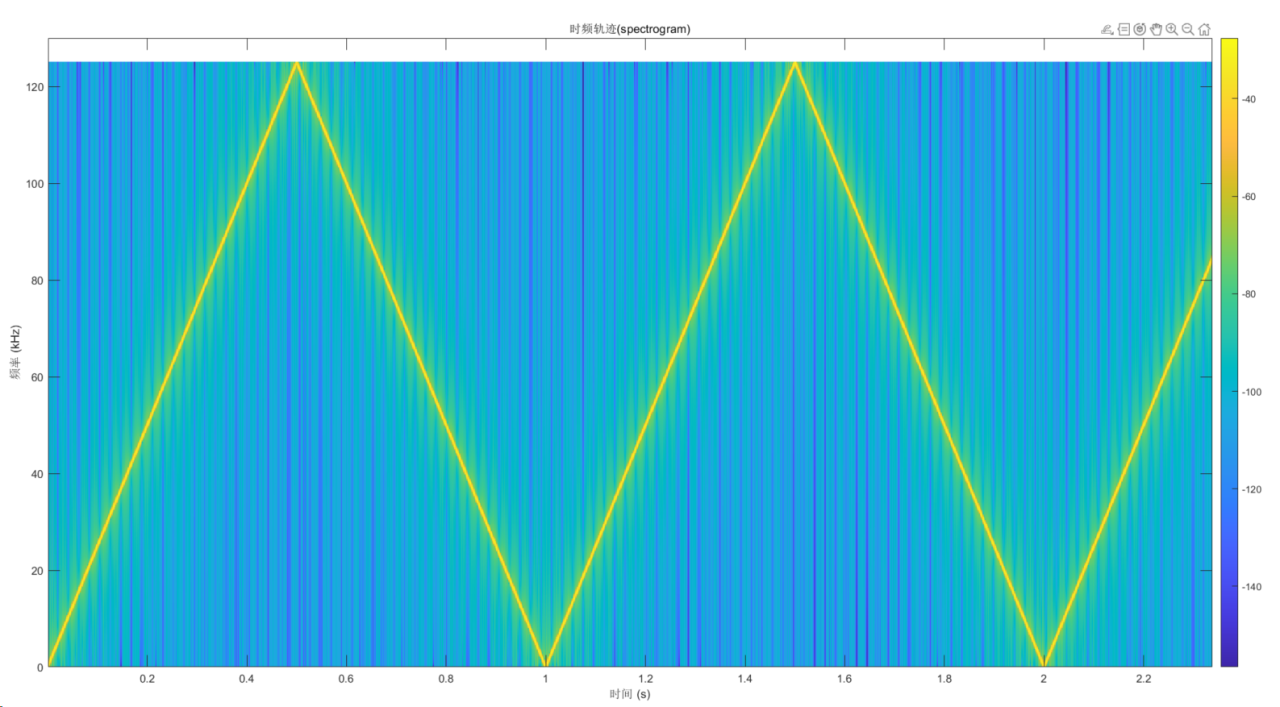
手动分帧计算时频图:
使用hanning窗的结果:

使用矩形窗的结果(FPGA中相当于用的也是矩形窗):
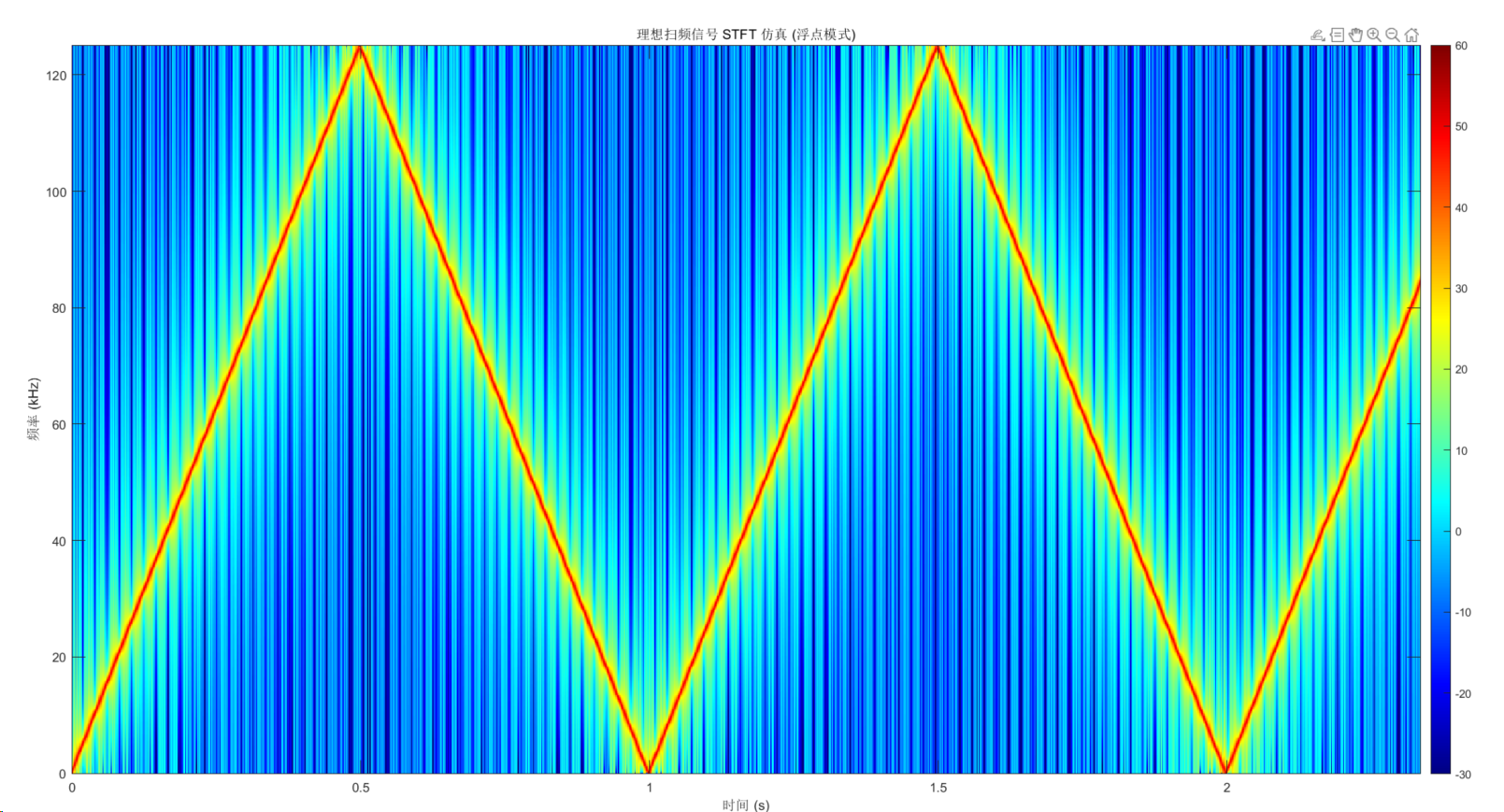
通过对比分析可知, 模拟仿真的结果和FPGA计算的时频图结果相似,通过动图也说明FPGA计算的结果没有问题。
那么问题来了,问什么先采集原始信号,再做STFT会得到不一样的结果呢?重新用250khz采集100hz~250khz的扫频信号,结果如下:
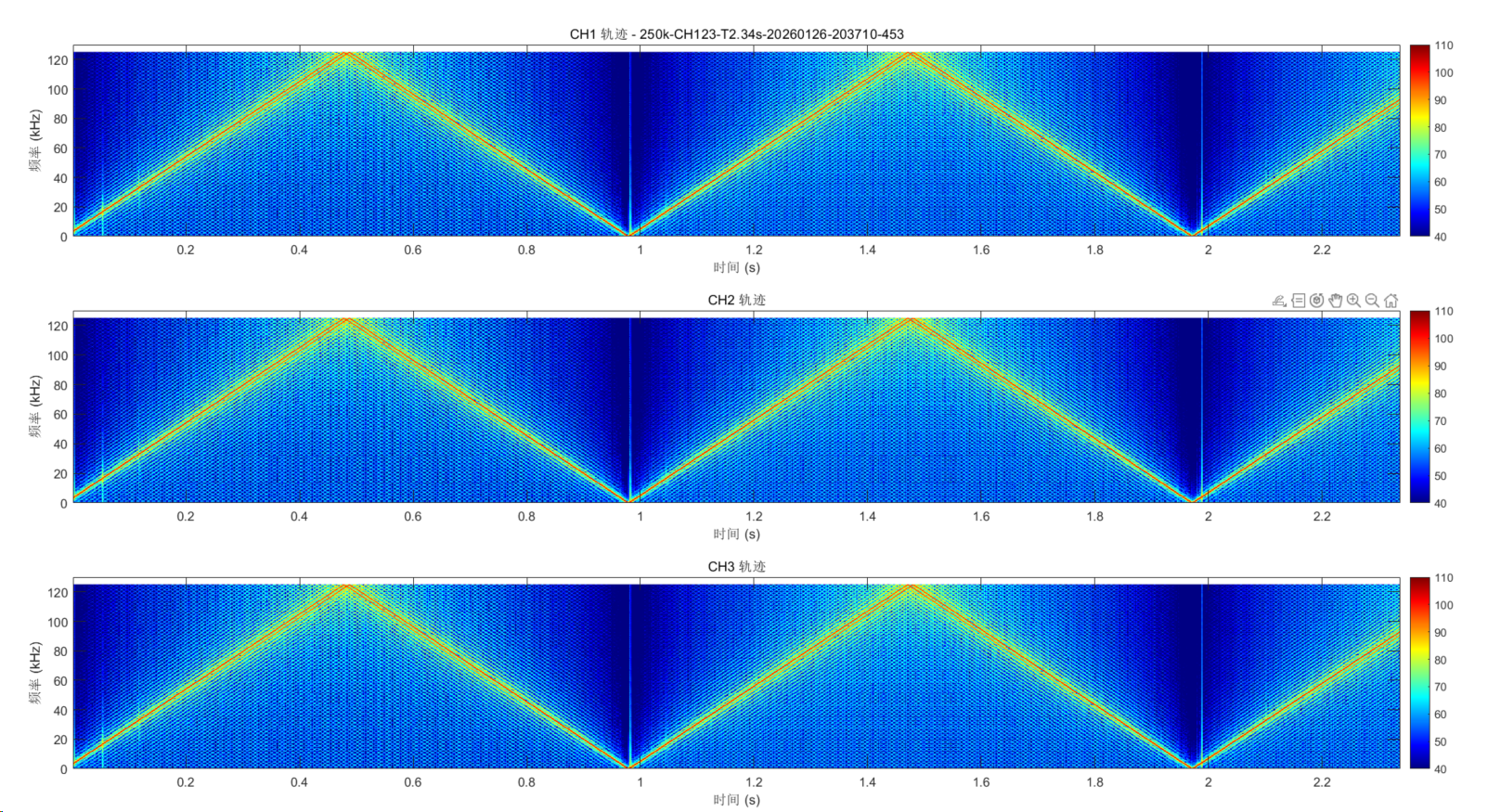
从动态视频图来看的确没有那么好的效果了。这是为什么呢?
AI解析:
针对你的疑问,我们直接来看 MATLAB 官方文档的定义以及它在信号处理中的底层逻辑。
默认窗函数 (Default Window)
在 MATLAB 的
spectrogram函数中,如果你将window_size指定为一个标量 (即只给定长度),它默认使用的是 Hamming 窗。
具体实现: MATLAB 会调用
hamming(window_size)。特性: Hamming 窗的旁瓣衰减约为
。这与 FPGA 中常用的**矩形窗(Rectangular Window)**或 Hann 窗在频谱泄露的表现上是不同的。如果你在 FPGA 中没有加窗(即默认矩形窗),那么两者的主瓣宽度和旁瓣高度就会产生明显的视觉差异。
2. 它会除以点数
吗?
不会。 这是导致你 MATLAB 结果与 FPGA 结果量级(Magnitude)巨大的最直接原因。
MATLAB 的行为:
spectrogram在底层调用fft。MATLAB 的fft函数实现的是标准的离散傅里叶变换公式:这个公式里没有任何归一化因子。因此,对于一个振幅为
的正弦波,其经过
点 FFT 后的峰值幅值大约是
(如果考虑双边谱且不计窗函数的增益影响)。
FPGA 的行为: 你在 Vivado 中配置 Xilinx FFT IP 核时,通常为了防止定点数溢出,会选择 Scaled 模式。在
的配置下,IP 核通常会在计算过程中通过每级移位实现总共
的缩放。
量级对齐:
这就是为什么 MATLAB 的结果是
,而 FPGA 只有
。
上面的分析我觉得是对的。重新画了一下:
动态的结果差不多,但是还是没有直接运算的好,就是除了主频点以外的地方,会出现波纹。
3. 为什么 FPGA 的结果"更符合"?
当你觉得 FPGA 的结果更符合预期时,通常是因为以下潜规则:
- 物理意义对齐: FPGA 的
缩放使得输出幅值与输入物理量的量级更接近(虽然差了倍数),而 MATLAB 的原始累加值超出了常规物理直觉。
对波纹的解释:
现在的量级(
)已经和 FPGA 对齐了,这说明缩放比例(Scaling)和数据位宽解析基本正确。
你看到的这些"波纹",在信号处理中被称为频谱泄露(Spectral Leakage) ,具体表现为矩形窗的 Sinc 函数旁瓣。
为什么会出现这些"波纹"?
当你使用
rectwin(矩形窗)时,时域上的截断相当于给信号乘了一个矩形脉冲。在频域上,这等同于信号的真实谱线与一个 Sinc 函数进行卷积。
矩形窗的特性: 它的主瓣最窄(分辨率高),但旁瓣非常高 (第一旁瓣仅比主瓣低
)。
物理表现: 只要你的信号频率不是正好落在 FFT 的整数 Bin(频率点)上,能量就会沿着 Sinc 函数的形状向周围扩散,形成你看到的这些波纹。
为什么 FPGA 的结果看起来更"干净"?
FPGA 的结果之所以没有明显的波纹,可能是以下原因:
定点数截断(Quantization):
- FPGA 内部使用定点运算(例如 16-bit 或 24-bit 输出)。那些幅度较小的旁瓣波纹在定点化过程中,可能因为值太小而被直接截断(Truncate)为 0 或者落在了底噪之下。
- MATLAB 使用双精度浮点运算,能够精准地计算出每一级微小的旁瓣,所以波纹清晰可见。
这个解释是有点道理的。
建议对比实验
为了确认"波纹"是否仅由窗函数引起,你可以尝试在 MATLAB 中切换到 Hamming 窗观察:
% 将 rectwin 换成 hamming 试试 [S, F, T] = spectrogram(data1, hamming(window_size), overlap, nfft, fs, 'yaxis');
- 如果切换后波纹消失了: 说明之前的波纹纯粹是矩形窗的数学特性。
2026-01-27-lhw:
经试验验证并没有改善,还是有波纹。
2026-01-27-lhw:总结
结论:FPGA 与 MATLAB 处理结果在幅值量级上具有高度一致性(约量级),验证了 FPGA 算法缩放策略(Scaling Schedule)的正确性。
-
频谱特征差异分析:
-
MATLAB 结果: 呈现出明显的矩形窗(Rectangular Window)特性,主频点两侧伴随典型的 Sinc 函数旁瓣波纹。由于 MATLAB 采用双精度浮点运算,能够精确捕捉频谱泄露的数学细节。
-
FPGA 结果: 谱线基底更为"干净",基本消除了低量级的旁瓣波纹。
-
-
原因解释: 定点化截断效应: FPGA 内部采用定点运算,微弱的旁瓣能量在位宽截断(Truncation)或舍入过程中落入 LSB(最低有效位)以下,从而起到天然的"噪声门"作用,使背景更加纯净。
-
时频图和动图结果不对应的原因
这种"对应不上"的感觉,其实揭示了信号处理中显示尺度 与硬件特性两个核心差异。
1. 线性尺度 vs 对数尺度 (最直观的原因)
动图/折线图 (Linear Scale): 你的动图使用的是线性纵轴 (幅值
量级)。在这种尺度下,主频点以外的旁瓣(波纹)虽然存在,但因为其幅值通常只有主频的
甚至更低,在视觉上会被压缩成贴近
的平线,显得非常"干净"。
时频图 (Logarithmic/dB Scale): 观察时频图的右侧色标(Colorbar),其范围是 40 到 110 。这是一个对数尺度,它会极大地放大低能量信号。那些在线性图中看不见的"波纹"(旁瓣),在 dB 尺度下会被映射为明显的颜色亮线。
结论: 时频图里的那些"垂直细线",实际上就是动图里主频两边那些微小"波纹"在时间轴上的堆叠。
如果动图换成对数的,就符合时频图了:
2. 频谱泄露在时频图中的表现
垂直拖尾现象: 你提到的时频图里有很多垂直的纹路,这正是矩形窗 (Rectangular Window) 的典型特征。
物理机制: 扫频信号在快速变化时,矩形窗产生的
函数旁瓣非常高(第一旁瓣仅比主频低
)。由于时频图显示的是动态范围极大的 dB 能量,这些旁瓣能量在每一帧都会向上、下频率扩散,形成了你看到的垂直"底噪"背景。
3. FPGA 的"天然滤波"效应
FPGA 动图的对称性: FPGA 动图表现得异常干净且对称,是因为 FPGA 采用了定点数(Fixed-point)计算。
截断效应 (Truncation): 那些在 MATLAB 浮点运算中产生的微小旁瓣能量,在 FPGA 的定点位宽(如 24-bit)截断过程中,因为值太小而无法达到最低有效位(LSB),被直接归零了。
视觉差异: 这种定点化过程起到了"噪声门"的作用,导致 FPGA 的动态图看起来比 MATLAB 的仿真结果更"完美",基本只剩下了最核心的主频分量。
核心对比总结表
特性 动图 (折线) 时频图 (Spectrogram) 观察重点 瞬时幅值、缩放一致性 全程频率轨迹、动态范围 显示动态 较窄 (主要看大信号) 极宽 (小能量细节毕现) 波纹去向 隐藏在 刻度附近
表现为背景中的垂直亮线 对称性 理想 FFT 的数学特征 受扫频斜率和窗口重叠影响
2.3.2时间码结果
时间戳结果如下:
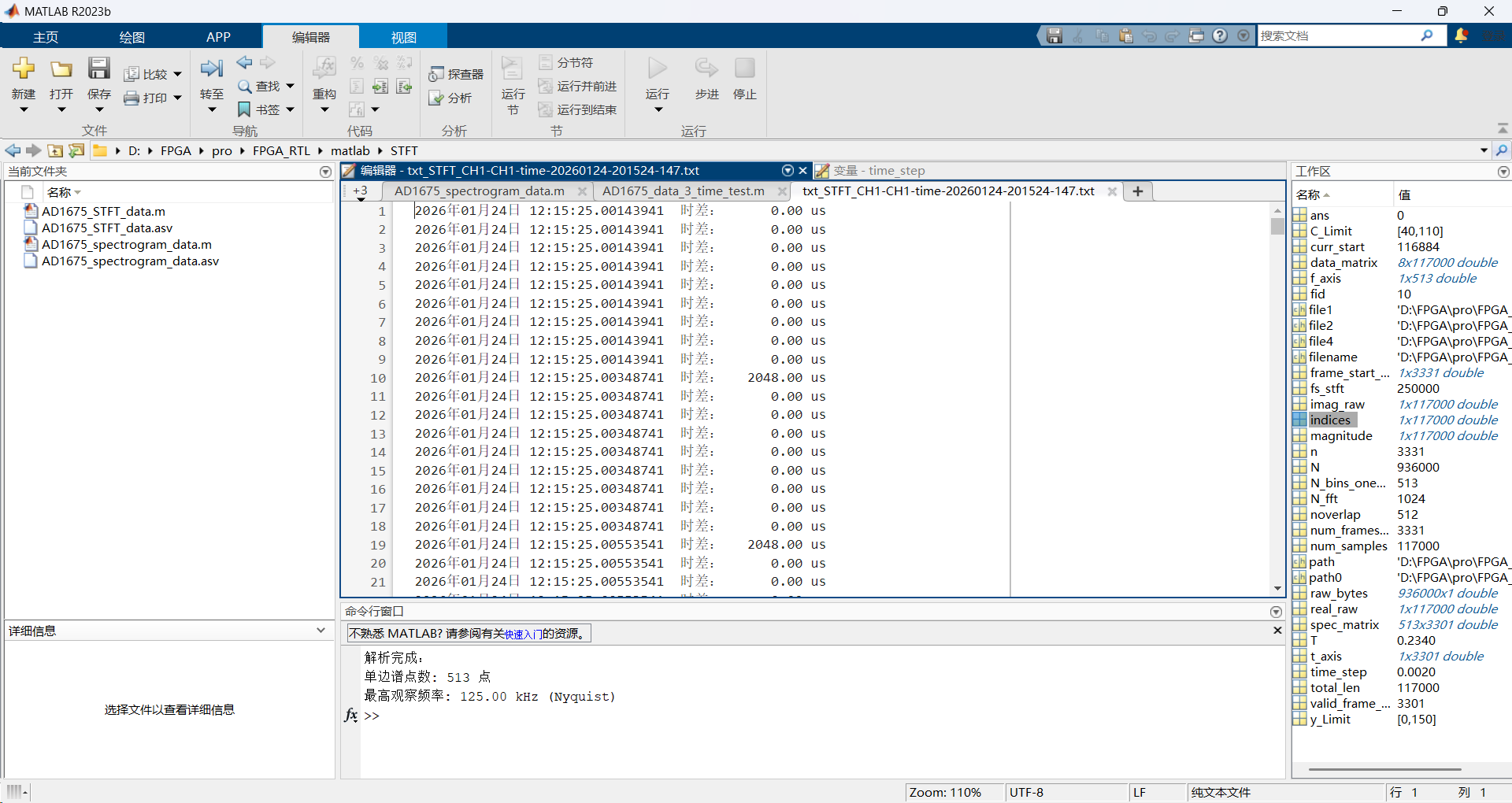
从图中来看,时间码符合预期要求,每一次的运算结果都是此次的第一个数据点的采集时间。以下是对时间码的详细解释:
(1)同一帧运算结果时间戳相同
在图中,可以看到连续 9 行的时间戳完全相同(均为 12:15:25.00143941),且"时差"为 0.00 us。分析如下:
-
硬件打标频率 :FPGA 只在每一帧 STFT 计算开始 (即
indices == 0时)捕获一次 64 位硬件时间戳。 -
数据包拆分 :一帧完整的 1024 点频谱需要占用约
个 UDP 数据包。
-
结论 :由于这 9 个数据包都属于同一次 FFT 运算的结果,硬件给这 9 个包打上了完全相同的"帧起始时间戳"。因此,你在解析时会看到时间码在这一帧的传输时间内保持不变。
(2)为什么跳变值正好是 2048.00 μs?
在文本的第 10 行和第 19 行,时间戳发生了跳变,增加值精确地为 2048.00 us。
-
理论步进对齐 :这与在 MATLAB 脚本中计算的
time_step完全吻合: -
物理意义 :这证明了硬件的 Hop Size(步进) 逻辑是准确的。每隔 512 个采样点,硬件就准时触发下一次 STFT 并更新时间戳。
3.测试过程中遇到的问题
3.1时间同步的问题:硬复位对齐 vs. 连续打标模式
在"数字采集系统"的研发中,如何处理每秒起始的同步信号(PPS/second_start)是一个核心的工程权衡。以下是对这两种方案的详细描述:
方案一:硬复位模式(Hard Reset Mode)------ 追求绝对对齐
这是目前工程中采用的方案,每当 second_start(秒脉冲)到来时,系统会执行强制复位逻辑。

-
实现机制:
-
清空缓冲区:瞬间清空 RAM 和 FIFO 中的历史数据。
-
逻辑归零:STFT 状态机、计数器和 FFT IP 核流水线全部重置。
-
重新起始:从秒起始后的第一个有效采样脉冲开始重新填充数据。
-
-
优缺点分析:
-
优点:
-
绝对对齐:每一秒的第一帧 STFT 处理窗口都严格对应绝对时间秒脉冲后的数据(距离上升沿多远就不知道了)。
-
结构整齐:由于每秒都"重开",每一秒内生成的数据帧数是恒定的,极大简化了后端大规模数据的检索与多设备(如多台探测仪或多颗卫星)的相位比对。
-
-
缺点:
- 数据断层:秒与秒之间的数据流不连续,导致跨秒的瞬态物理现象可能被截断。
-
AI解析:
STFT为什么从秒开始的原因:
在 FPGA 信号处理(尤其是像您所在的 实验室涉及的地球物理或精密电磁探测领域)中,"从秒开始"并不是为了节省资源,而是为了确保数据的"物理意义"和"多机同步"。
如果不从秒起始(PPS)信号开始采样,采集到的数据就会变成"无根之木"。以下是几个核心原因:
建立绝对时间基准 (Timestamping)
代码中的
real_time是一个 64 位的计数器。如果随机时刻开始采样:
问题: 你只知道两个采样点之间相隔 200ns(5MHz),但你不知道第一个点到底是某秒内的第几个微秒。
对齐后: 当
second_start来临时,我们明确知道此时是 T = 0.000,000s。这样,STFT 计算出的每一个频率成分都能精确对应到 GPS 时间轴上。这对于后期分析地震波、电磁扰动等瞬态信号至关重要。防止跨秒污染: 将
STFT_inst的复位也接入秒同步复位。这样每秒开始时,STFT 内部窗口会被清空,确保第一帧输出纯粹属于"新的一秒"。多通道与多设备同步 (Synchronization)
假设你有三台探测仪分布在不同的山头采集同一组地震信号:
不从秒开始: 每台仪器上电时间不同,它们的采样点在时间轴上会前后错开。当你把三台设备的数据汇总到电脑里分析时,你无法通过互相关算法计算信号的相位差。
从秒开始: 所有设备都在接收到同一个秒脉冲(PPS)的瞬间启动。这样,所有设备采集到的"第 1000 个点"代表的都是同一个物理时刻。
STFT 窗函数的相位一致性
STFT 是分段处理的。如果每一秒的处理逻辑都从秒脉冲重新"归零":
数学上的好处: 你可以保证每一秒的第一帧 STFT 窗口始终覆盖的是从 [0, N-1]个采样点。这使得处理逻辑非常整齐,避免了跨秒处理时窗口跨度不确定的复杂性。
如果不归零,随着时间推移,采样率的小微偏移会导致处理窗口在秒与秒之间发生漂移,增加算法复杂性。
方案二:连续打标模式(Continuous Tagging Mode)------ 追求物理连续性
如果系统更看重物理现象的完整性,则应采用"不停机采样"方案。
-
实现机制:
-
不停机运行 :
second_start到来时,不复位 RAM,不中断 STFT 逻辑。 -
时间戳锁存(Latch):在秒脉冲触发的瞬间,锁存当前的绝对时间计数器或样点序号。
-
-
优缺点分析:
-
优点:
-
完美连续:频谱图在秒边界处平滑过渡,无任何视觉断层。
-
信息完整:保留了上电后及秒交界处的所有采样样点,不丢失任何物理细节。
-
-
缺点:
-
样点滑移 :受晶振温漂影响,物理上的每一秒内采集到的样点数会有微小波动(例如有时是 250,000 个点,有时是 250,001 个点)。(其实我觉得这个影响不大,因为时间戳是GPS的时间,属于绝对时间,也可以用来做同步)
-
解析难度增加:后端 MATLAB 在进行长时序列分析时,无法再使用固定的"秒+帧偏移"算法,必须根据每个数据包内嵌入的同步标记动态修正时间轴(但只要采集的时差没有错误,也可以固定的"秒+帧偏移"算法来画时间轴)。
-
-
我感觉拥有绝对时间的时候这种方案也是可以做到数据同步的。
建议:若追求极致的科研数据连续性,建议将硬复位优化为"软同步"打标逻辑;若追求系统多机协同的可靠性与工程解析的简便性,目前的硬复位方案更具鲁棒性。
初始同步策略:从"无序"到"确定"的必然选择
在数字采集系统的设计初期,主动丢弃首个秒脉冲(PPS)之前的数据确保数据的物理溯源性 与时间确定性。
-
无序状态(Unordered State):系统上电瞬间,FPGA 逻辑与 ADC 虽进入运行态,但此时系统时钟计数器缺乏绝对参考基准。此时的采样数据由于无法映射至精确的毫秒/微秒偏移,在物理上被定义为"漂移数据"。
-
对齐状态(Aligned State) :直至
second_start(由 GPS 或高稳晶振提供的 PPS 信号)触发同步脉冲,系统时间基准(Time-base)完成强制对齐。 -
设计结论:丢弃首个 PPS 之前的数据,实质上是建立了"无效数据过滤墙"。这不仅保证了后续 STFT 等滑窗算法的时间轴连续性,更彻底杜绝了因初始相位不确定导致的时间戳漂移风险。
之后也不在进行秒脉冲的硬复位。
3.2时间不对的现象
采集0.234的数据,画图时却显示6.7秒的数据,现象如下图所示:
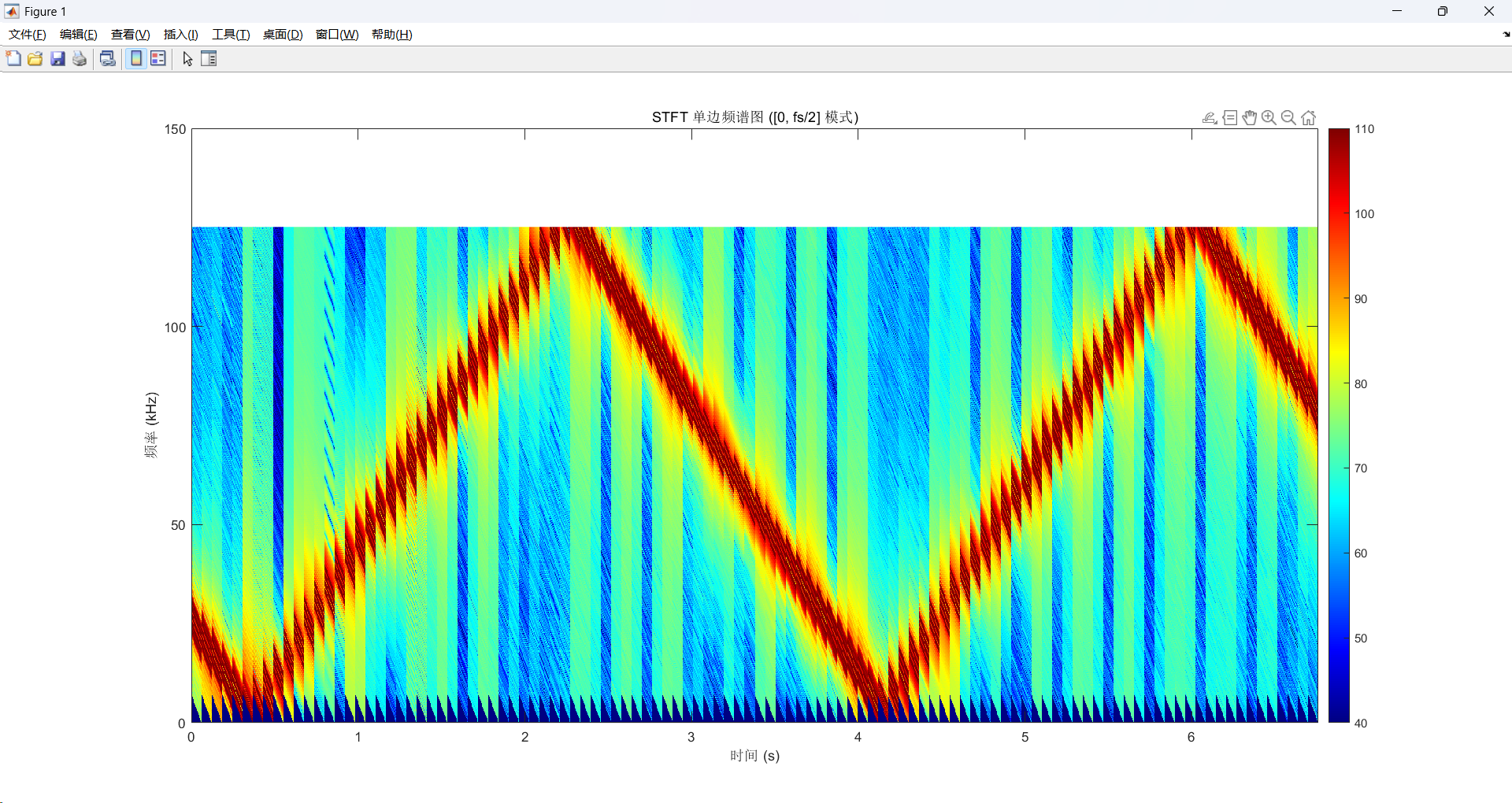
该现象的出现是因为没有把数据打包的方式和数据解析的方式结合起来。
首先是数据打包的方式。FPGA上传给上位机的一帧数据里面包含了117Byte的STFT运算结果,为了完整发送一次STFT的结果即1024Byte,则需要在最后一帧数据包补充29个0,使总数据为1053Byte,这样一次数据的运算结果可以分为9帧数据包上传。
其次是matlab对数据的解析,是通过识别下标0,认为是这一帧的开始点,然后往后的1023个点都是这一帧运算结果。理论上,这种做法是没有问题,但是因为打包的时候多加了0,所以会有虚假零帧 的出现,如下图所示。从而使每一帧变为30帧,0.234*30=7.02, 然后因为采集的时间可能不是整数包,所以会有不完整的包,因此matlab会出现识别出了 3301 帧 完整的频谱数据的现象。采集一次STFT计算点数所需要的时间:
time_step = (N_fft - noverlap) / fs_stft=(1024-512)/250000= 2.048ms
所以出现3301*2.048=6.76s的时间轴。
 填充的数据0
填充的数据0
虚假零帧的现象:图中的三角形斜坡就是因为虚假零帧的现象,随着帧数的增加,初始的0个数越来越少,能量就会回归正常值,从而表现出三角斜坡的形式。
以上就是本次笔记的记录。