《数字信号处理》第 2 章 - z 变换与离散时间傅里叶变换（DTFT）

啊阿狸不会拉杆2026-01-28 8:11

目录

​前言

[2.1 序列的 z 变换](#2.1 序列的 z 变换)

[2.1.1 z 变换的定义](#2.1.1 z 变换的定义)

[2.1.2 z 变换的收敛域](#2.1.2 z 变换的收敛域)

[2.1.3 4 种典型序列的 z 变换的收敛域](#2.1.3 4 种典型序列的 z 变换的收敛域)

[2.1.4 z 反变换](#2.1.4 z 反变换)

[1. 围线积分法（留数法）](#1. 围线积分法（留数法）)

[2. 部分分式法（最常用）](#2. 部分分式法（最常用）)

[3. 长除法（幂级数法）](#3. 长除法（幂级数法）)

[2.1.5 z 变换的性质与定理](#2.1.5 z 变换的性质与定理)

[2.1.6 利用 z 变换求解差分方程](#2.1.6 利用 z 变换求解差分方程)

[2.2 s 平面到 z 平面的映射关系](#2.2 s 平面到 z 平面的映射关系)

[2.3 离散时间傅里叶变换（DTFT）------ 序列的傅里叶变换](#2.3 离散时间傅里叶变换（DTFT）—— 序列的傅里叶变换)

[2.3.1 序列的傅里叶变换定义](#2.3.1 序列的傅里叶变换定义)

[2.3.2 序列傅里叶变换的收敛性 ------DTFT 的存在条件](#2.3.2 序列傅里叶变换的收敛性 ——DTFT 的存在条件)

[2.3.3 序列傅里叶变换的主要性质](#2.3.3 序列傅里叶变换的主要性质)

[2.3.4 序列及其傅里叶变换的一些对称性质](#2.3.4 序列及其傅里叶变换的一些对称性质)

[2.3.5 周期性序列的傅里叶变换](#2.3.5 周期性序列的傅里叶变换)

[2.3.6 xa​(t)、x^a​(t)、x(n) 之间及各变换的关系](#2.3.6 xa(t)、x^a(t)、x(n) 之间及各变换的关系)

[2.4 离散线性移不变系统的频域表征](#2.4 离散线性移不变系统的频域表征)

[2.4.1 LSI 系统的描述](#2.4.1 LSI 系统的描述)

[2.4.2 LSI 系统的因果、稳定条件](#2.4.2 LSI 系统的因果、稳定条件)

[2.4.3 LSI 系统的频率响应 H(ejω) 及其特点](#2.4.3 LSI 系统的频率响应 H(ejω) 及其特点)

[2.4.4 频率响应的几何确定法](#2.4.4 频率响应的几何确定法)

[2.4.5 无限长单位冲激响应 (IIR) 系统与有限长单位冲激响应 (FIR) 系统](#2.4.5 无限长单位冲激响应 (IIR) 系统与有限长单位冲激响应 (FIR) 系统)

[2.5 本章部分内容涉及的 MATLAB 函数及例题](#2.5 本章部分内容涉及的 MATLAB 函数及例题)

核心函数总结

[综合例题：基于 z 变换和 DTFT 的信号分析](#综合例题：基于 z 变换和 DTFT 的信号分析)

习题

​编辑

总结

前言

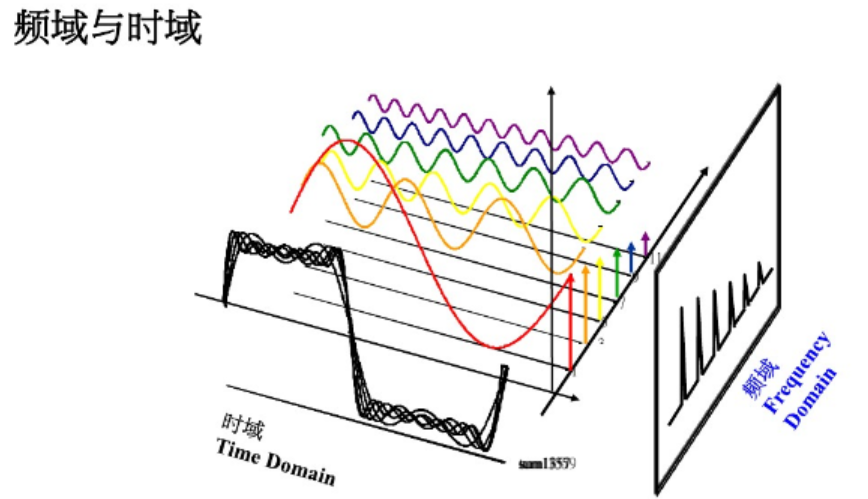
大家好！今天给大家梳理《数字信号处理》第 2 章的核心内容 ------z 变换与离散时间傅里叶变换（DTFT）。这一章是数字信号处理的核心基础，从 z 变换的定义、收敛域，到 DTFT 的性质，再到离散系统的频域分析，都会用通俗易懂的语言讲解，搭配 MATLAB 实战代码和直观的对比图，帮大家彻底吃透知识点。

2.1 序列的 z 变换

2.1.1 z 变换的定义

2.1.2 z 变换的收敛域

2.1.3 4 种典型序列的 z 变换的收敛域

MATLAB 验证：单位阶跃序列（右边序列）的 z 变换与 ROC

Matlab 复制代码 
% 2.1.3 典型序列z变换 - 单位阶跃序列u(n)
% 功能：计算单位阶跃序列的z变换并绘制时域图
% 作者：CSDN博主
% 日期：2026
clc; clear; close all;  % 清理工作区、命令行，关闭所有图形窗口

%% 1. 生成单位阶跃序列（截取前20点）
n = 0:19;               % 数值变量：时域索引（0到19）
x = ones(1, length(n)); % 单位阶跃序列：前20点全为1
% 校验序列生成是否正确
if ~isvector(x) || length(x) ~= length(n)
    error('序列生成错误：x必须是与n长度相同的向量');
end

%% 2. 符号计算z变换（避免变量名冲突，用n_sym作为符号变量）
syms z n_sym;           % 符号变量：z为复变量，n_sym为符号索引（与数值n区分）
Xz = ztrans(sym('1'), n_sym, z); % 单位阶跃序列u(n)的z变换（对符号变量n_sym计算）
disp('单位阶跃序列u(n)的z变换：');
disp(Xz);
disp('收敛域：|z| > 1');

%% 3. 绘制序列时域图
figure('Name','单位阶跃序列时域图','Position',[100,100,800,500]); % 指定窗口位置和大小
stem(n, x, 'filled', 'Color', 'b');  % 绘制填充型茎状图
xlabel('n (时域索引)','FontSize',12); % x轴标签
ylabel('x(n) = u(n)','FontSize',12);  % y轴标签
title('单位阶跃序列u(n)（前20点）','FontSize',14,'FontWeight','bold'); % 标题
grid on;  % 显示网格
set(gca,'FontSize',10); % 设置坐标轴字体大小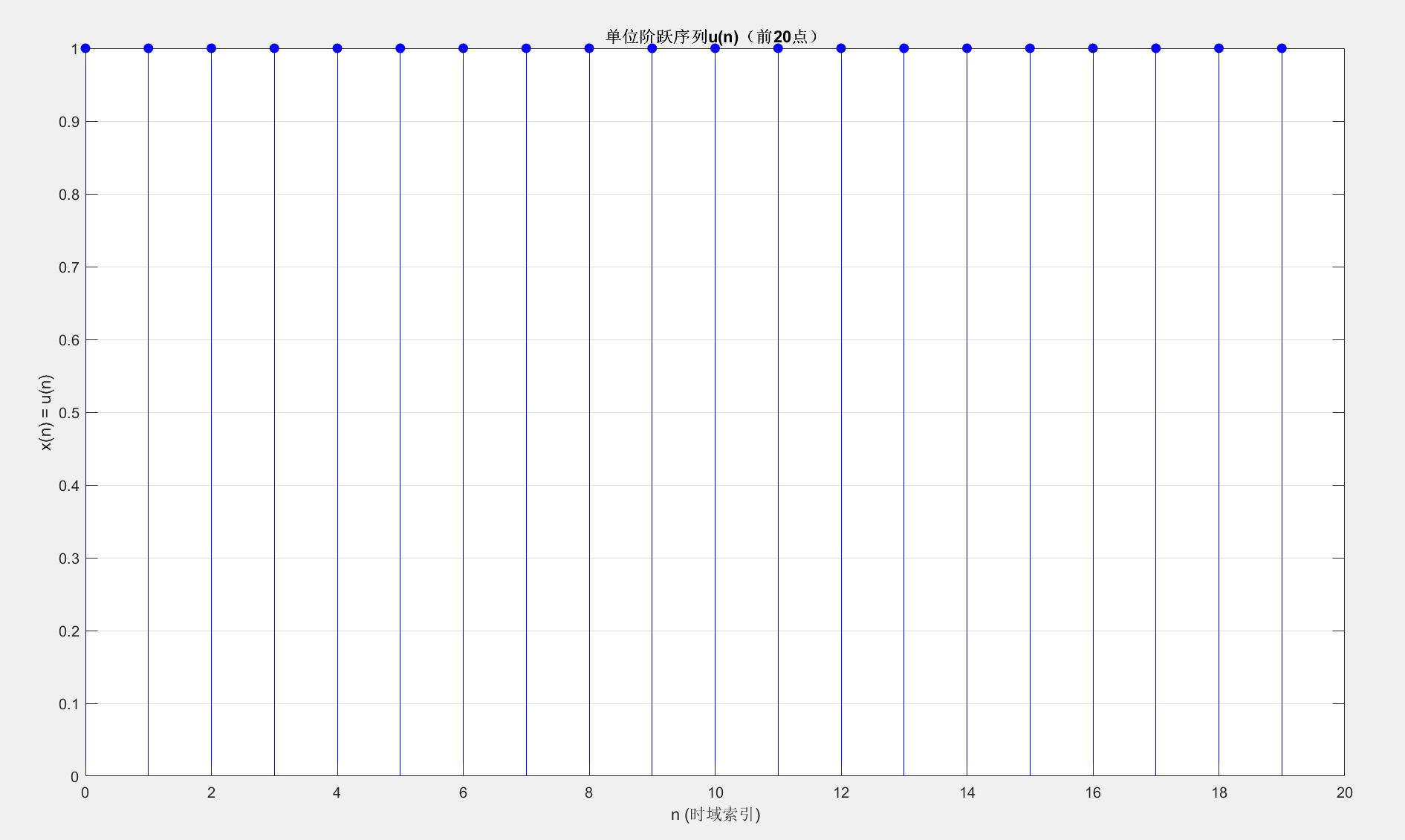

运行结果：z 变换为 z/(z−1)，收敛域 ∣z∣>1，时域图是从 n=0 开始的全 1 序列。

2.1.4 z 反变换

z 反变换是从 X(z) 恢复时域序列 x(n) 的过程，常用 3 种方法：

1. 围线积分法（留数法）
2. 部分分式法（最常用）

MATLAB 实战：部分分式法求 z 反变换

复制代码 
% 2.1.4 z反变换 - 部分分式法
clc; clear; close all;

% 例：X(z) = z/(z^2 - 1.5z + 0.5)，ROC |z|>1（因果序列）
num = [1 0];          % 分子：z
den = [1 -1.5 0.5];   % 分母：z^2 -1.5z +0.5

% 部分分式分解
[r, p, k] = residuez(num, den);
disp('部分分式系数：');
disp(r);
disp('极点：');
disp(p);

% 求z反变换（生成前20点序列）
n = 0:19;
x = impz(num, den, length(n));

% 绘制时域序列
figure('Name','z反变换结果（部分分式法）');
stem(n, x, 'filled', 'Color', 'r');
xlabel('n'); ylabel('x(n)');
title('X(z) = z/(z^2 -1.5z +0.5) 的z反变换（因果序列）');
grid on;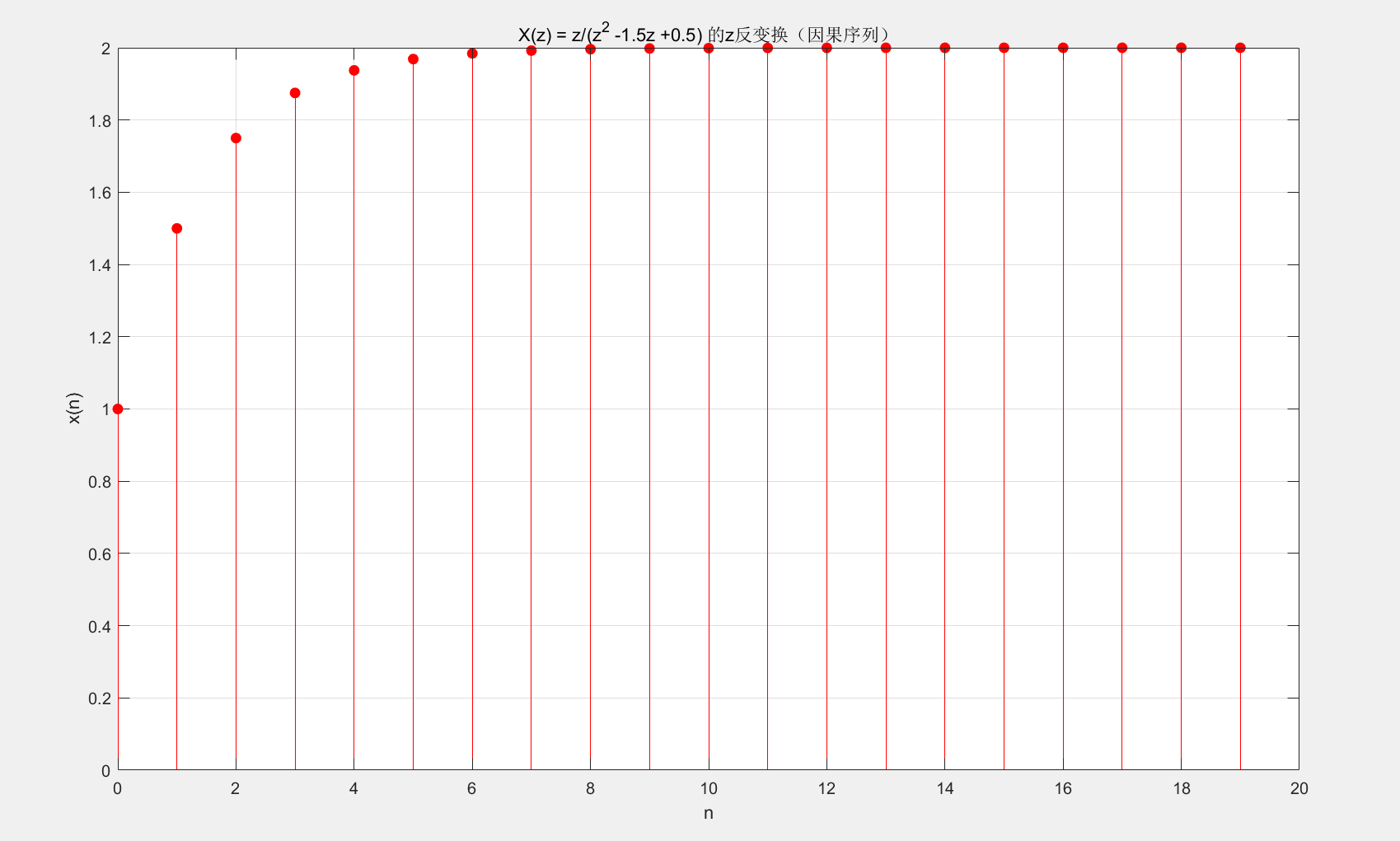

运行结果：分解得到极点 p=[1, 0.5]，反变换序列为 x(n)=2⋅1n−1⋅(0.5)n（n≥0）。

3. 长除法（幂级数法）

将 X(z) 展开为 z−n 的幂级数，系数即为 x(n)。适合简单的有理分式，但只能得到前 N 点序列（无法直接得到闭式解）。

2.1.5 z 变换的性质与定理

z 变换的核心性质（简化计算，类比傅里叶变换）：

2.1.6 利用 z 变换求解差分方程

离散系统的差分方程（线性常系数）：

求解步骤：

  1. 对差分方程两边做 z 变换（利用时移性质）；
  2. 整理得到系统函数 H(z)=Y(z)/X(z)；
  3. 求 Y(z) 的 z 反变换，得到 y(n)。

MATLAB 实战：z 变换求解差分方程

复制代码 
% 2.1.6 利用z变换求解差分方程
% 例：求解 y(n) - 1.5y(n-1) + 0.5y(n-2) = x(n)，x(n)=u(n)，初始条件y(-1)=y(-2)=0
clc; clear; close all;

% 定义差分方程系数
a = [1 -1.5 0.5];  % 输出y的系数
b = [1];           % 输入x的系数

% 生成输入序列x(n)=u(n)（前30点）
n = 0:29;
x = ones(1, length(n));

% 求解差分方程
y = filter(b, a, x);

% 绘制输入输出序列对比
figure('Name','差分方程求解结果');
subplot(2,1,1);
stem(n, x, 'filled', 'Color', 'b');
xlabel('n'); ylabel('x(n)');
title('输入序列 x(n) = u(n)');
grid on;

subplot(2,1,2);
stem(n, y, 'filled', 'Color', 'r');
xlabel('n'); ylabel('y(n)');
title('输出序列 y(n)（差分方程解）');
grid on;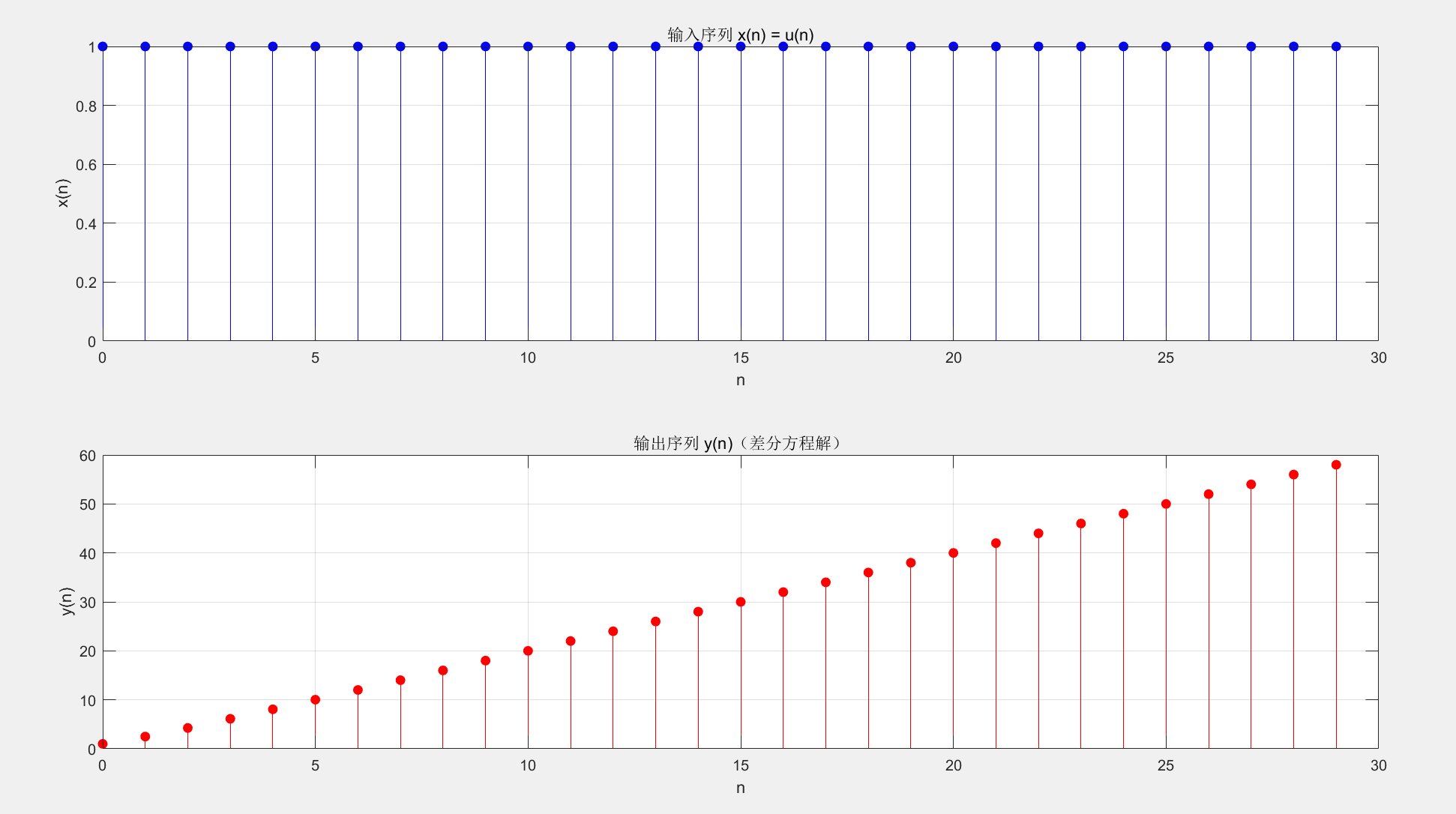

运行结果：输出序列 y(n) 收敛到 2，符合理论解 y(n)=2−(0.5)n（n≥0）。

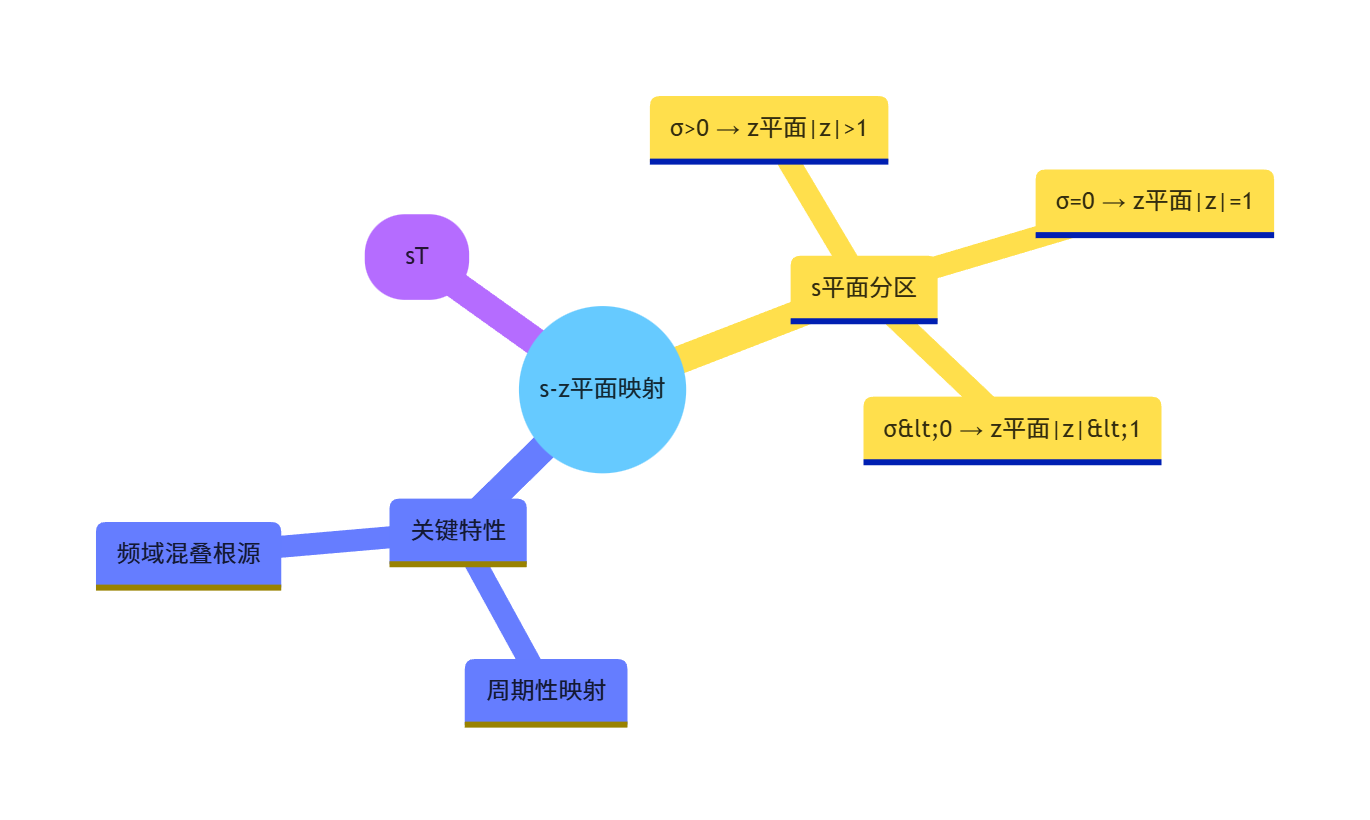
2.2 s 平面到 z 平面的映射关系

核心结论：

思维导图

2.3 离散时间傅里叶变换（DTFT）------ 序列的傅里叶变换

2.3.1 序列的傅里叶变换定义

核心理解 ：DTFT 是 z 变换在 ∣z∣=1（z 平面单位圆）上的特例，ω 是数字角频率（单位：rad），反映序列的频域特性。

2.3.2 序列傅里叶变换的收敛性 ------DTFT 的存在条件

DTFT 收敛的充要条件：序列 x(n) 绝对可和，即：

补充：

  • 绝对可和的序列（如衰减序列）一定存在 DTFT；
  • 非绝对可和但平方可和的序列（如正弦序列），DTFT 以 "冲激" 形式存在（周期序列）；
  • 因果稳定系统的单位冲激响应 h(n) 绝对可和，因此其频率响应存在。

2.3.3 序列傅里叶变换的主要性质

2.3.4 序列及其傅里叶变换的一些对称性质

对称性质是 DTFT 的核心（简化频域分析），核心结论：

MATLAB 实战：实序列 DTFT 的对称性质验证

Matlab 复制代码 
% 2.3.4 实序列DTFT的对称性质验证
% 功能：验证实序列的DTFT幅度偶对称、相位奇对称特性
% 说明：无隐形字符，可直接运行，包含自定义DTFT函数和鲁棒性校验
clc; clear; close all;

%% 1. 生成实序列：11点矩形窗序列（中心在n=0）
n = -5:5;                  % 时域索引，对称区间[-5,5]
x = rectwin(11)';          % 生成11点矩形窗（列向量）
% 校验序列维度：确保x和n长度一致
if length(x) ~= length(n)
    error('序列x和索引n的长度必须一致！');
end
x = x(:)';                 % 统一转为行向量，避免维度匹配问题

%% 2. 计算DTFT（频域高精度采样）
N = 1024;                  % 频域采样点数（越高越精细）
omega = linspace(-pi, pi, N);  % 数字角频率范围[-π, π]
X = dtft(x, n, omega);     % 调用自定义DTFT函数计算

%% 3. 提取幅度和相位（优化相位跳变，更易观察对称性）
magX = abs(X);             % 幅度谱（偶对称）
phaseX = angle(X);         % 相位谱（奇对称）
% 相位unwrap：消除π附近的跳变，让奇对称更直观
phaseX = unwrap(phaseX);

%% 4. 绘制对称性质对比图（优化可视化效果）
figure('Name','实序列DTFT的对称性质','Position',[100,100,900,600]);
% 幅度谱（偶函数）
subplot(2,1,1);
plot(omega, magX, 'LineWidth', 1.5, 'Color', '#1f77b4');
xlabel('\omega (rad)','FontSize',11); 
ylabel('|X(e^{j\omega})|','FontSize',11);
title('幅度谱（偶函数：关于\omega=0对称）','FontSize',12,'FontWeight','bold');
grid on; grid minor;  % 显示主次网格
axis tight;
% 相位谱（奇函数）
subplot(2,1,2);
plot(omega, phaseX, 'LineWidth', 1.5, 'Color', '#ff7f0e');
xlabel('\omega (rad)','FontSize',11); 
ylabel('∠X(e^{j\omega}) (rad)','FontSize',11);
title('相位谱（奇函数：关于\omega=0反对称）','FontSize',12,'FontWeight','bold');
grid on; grid minor;
axis tight;

%% 自定义DTFT计算函数（鲁棒性优化）
function X = dtft(x, n, omega)
    % DTFT: 计算离散时间傅里叶变换
    % 输入参数：
    %   x      - 输入实/复序列（行向量）
    %   n      - 序列对应的时域索引（行向量）
    %   omega  - 数字角频率数组（rad）
    % 输出参数：
    %   X      - DTFT结果（复数值数组）
    
    % 输入参数校验
    if ~isvector(x) || ~isvector(n) || ~isvector(omega)
        error('输入x、n、omega必须为向量！');
    end
    x = x(:)';  % 统一转为行向量
    n = n(:)';
    omega = omega(:)';
    
    % 初始化输出
    X = zeros(1, length(omega));
    % 逐点计算DTFT
    for k = 1:length(omega)
        % 核心公式：X(e^jω) = Σx(n)e^(-jωn)
        X(k) = sum(x .* exp(-1j * omega(k) * n));
    end
end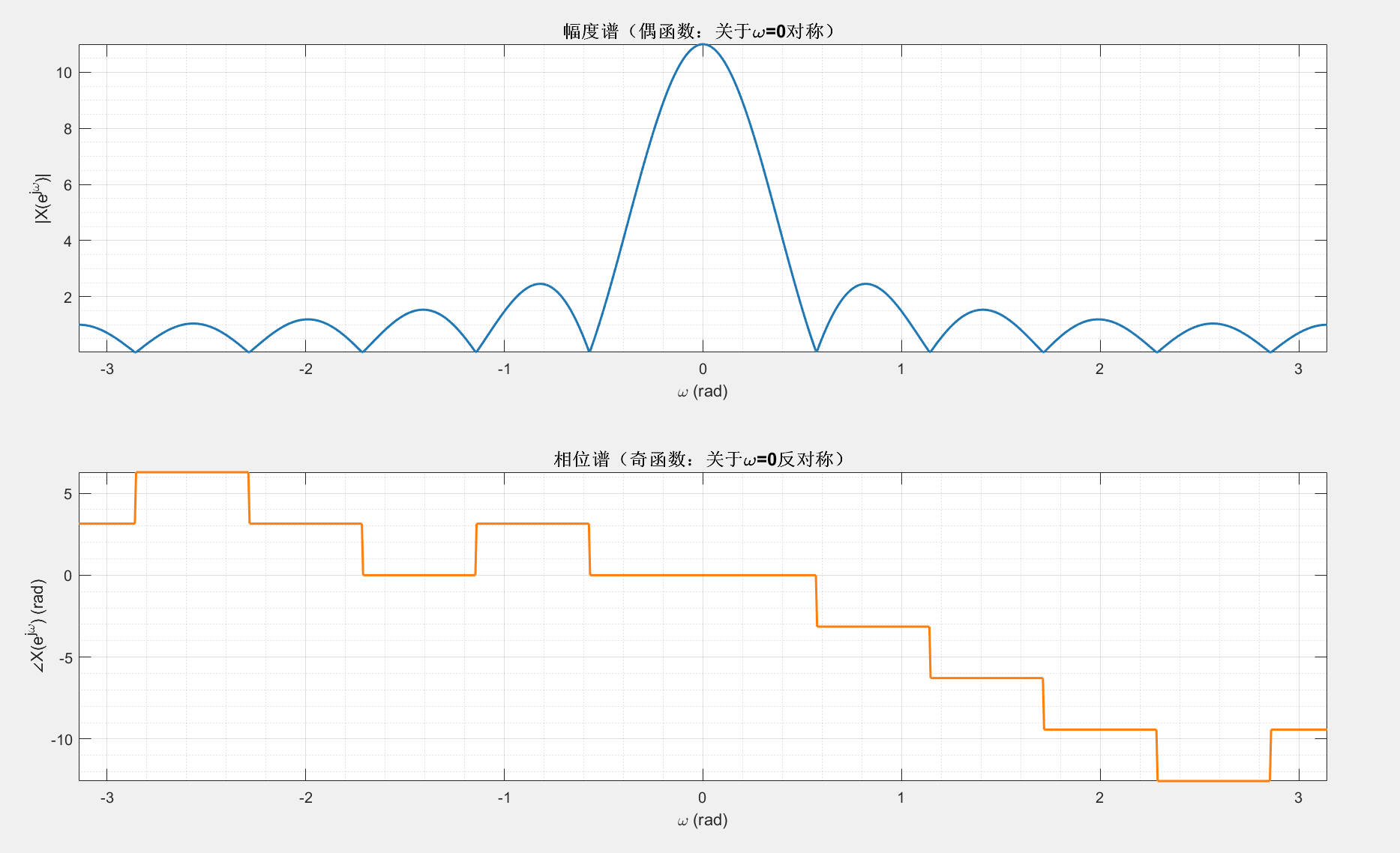

运行结果：幅度谱关于ω=0对称（偶函数），相位谱关于ω=0反对称（奇函数），验证了实序列的对称性质。

2.3.5 周期性序列的傅里叶变换

MATLAB 实战：周期方波序列的 DTFT

Matlab 复制代码 
% 2.3.5 周期性序列的DTFT
% 功能：生成周期方波序列并计算其DTFT，验证周期序列DTFT的冲激串特性
% 说明：内置dtft自定义函数，无外部依赖，可直接运行
clc; clear; close all;

%% 1. 生成周期N=8的方波序列（截取3个周期：-16~15，共32点）
N = 8;                  % 序列周期
n_total = -16:15;       % 时域索引范围（3个完整周期）
x = zeros(1, length(n_total));  % 初始化序列

% 生成周期方波：一个周期内前4点为1，后4点为0
for i = 1:length(n_total)
    n_mod = mod(n_total(i), N);  % 计算当前点的周期内索引
    % 修正mod函数负数处理问题（确保n_mod在0~N-1范围内）
    if n_mod < 0
        n_mod = n_mod + N;
    end
    if n_mod >= 0 && n_mod < 4
        x(i) = 1;
    end
end

%% 2. 计算DTFT（频域高精度采样）
omega = linspace(-pi, pi, 1024);  % 数字角频率范围[-π, π]
X = dtft(x, n_total, omega);     % 调用内置的dtft函数

%% 3. 绘制时域序列和频域DTFT图
figure('Name','周期方波序列的DTFT','Position',[100,100,900,600]);
% 子图1：时域周期方波序列
subplot(2,1,1);
stem(n_total, x, 'filled', 'Color', '#1f77b4', 'LineWidth', 1);
xlabel('n (时域索引)','FontSize',11);
ylabel('x(n)','FontSize',11);
title(['周期N=', num2str(N), '的方波序列（3个周期）'],'FontSize',12,'FontWeight','bold');
grid on; grid minor;  % 显示主次网格
axis tight;

% 子图2：频域DTFT幅度谱（冲激串形式）
subplot(2,1,2);
plot(omega, abs(X), 'LineWidth', 1.5, 'Color', '#ff7f0e');
xlabel('\omega (rad)','FontSize',11);
ylabel('|X(e^{j\omega})|','FontSize',11);
title('周期序列的DTFT（冲激串形式）','FontSize',12,'FontWeight','bold');
grid on; grid minor;
axis tight;
% 标注冲激位置（对应周期序列的谐波频率：2πk/N）
hold on;
for k = -4:4
    omega_k = 2*pi*k/N;  % 谐波频率位置
    if omega_k >= -pi && omega_k <= pi  % 仅标注显示范围内的冲激
        plot(omega_k, max(abs(X))*0.95, 'ro', 'MarkerSize', 6, 'DisplayName', '谐波位置');
    end
end
legend('DTFT幅度谱','谐波冲激位置','Location','best');
hold off;

%% 内置DTFT自定义函数（无需外部依赖）
function X = dtft(x, n, omega)
    % DTFT: 计算离散时间傅里叶变换
    % 输入参数：
    %   x      - 输入序列（行向量）
    %   n      - 序列对应的时域索引（行向量）
    %   omega  - 数字角频率数组（rad）
    % 输出参数：
    %   X      - DTFT结果（复数值数组）
    
    % 输入参数校验
    if ~isvector(x) || ~isvector(n) || ~isvector(omega)
        error('输入x、n、omega必须为向量！');
    end
    % 统一转为行向量，避免维度匹配问题
    x = x(:)';
    n = n(:)';
    omega = omega(:)';
    
    % 初始化DTFT结果
    X = zeros(1, length(omega));
    % 逐点计算DTFT核心公式：X(e^jω) = Σx(n)e^(-jωn)
    for k = 1:length(omega)
        X(k) = sum(x .* exp(-1j * omega(k) * n));
    end
end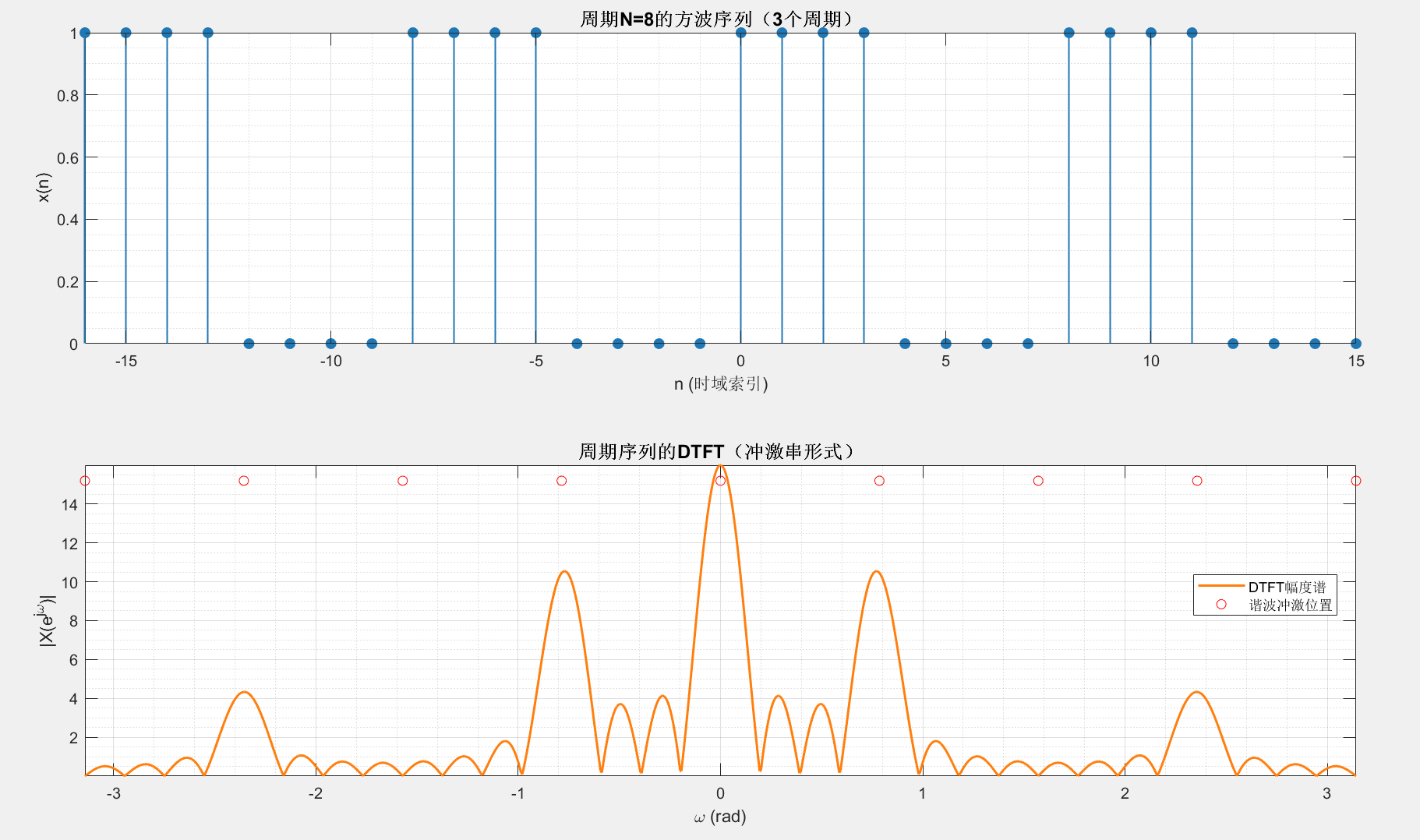

运行结果：频域图呈现冲激串特征，冲激位置对应 ω=2πk/8（k 为整数），验证了周期序列 DTFT 的特性。

2.3.6 xa​(t)、x^a​(t)、x(n) 之间及各变换的关系

变换关系流程图

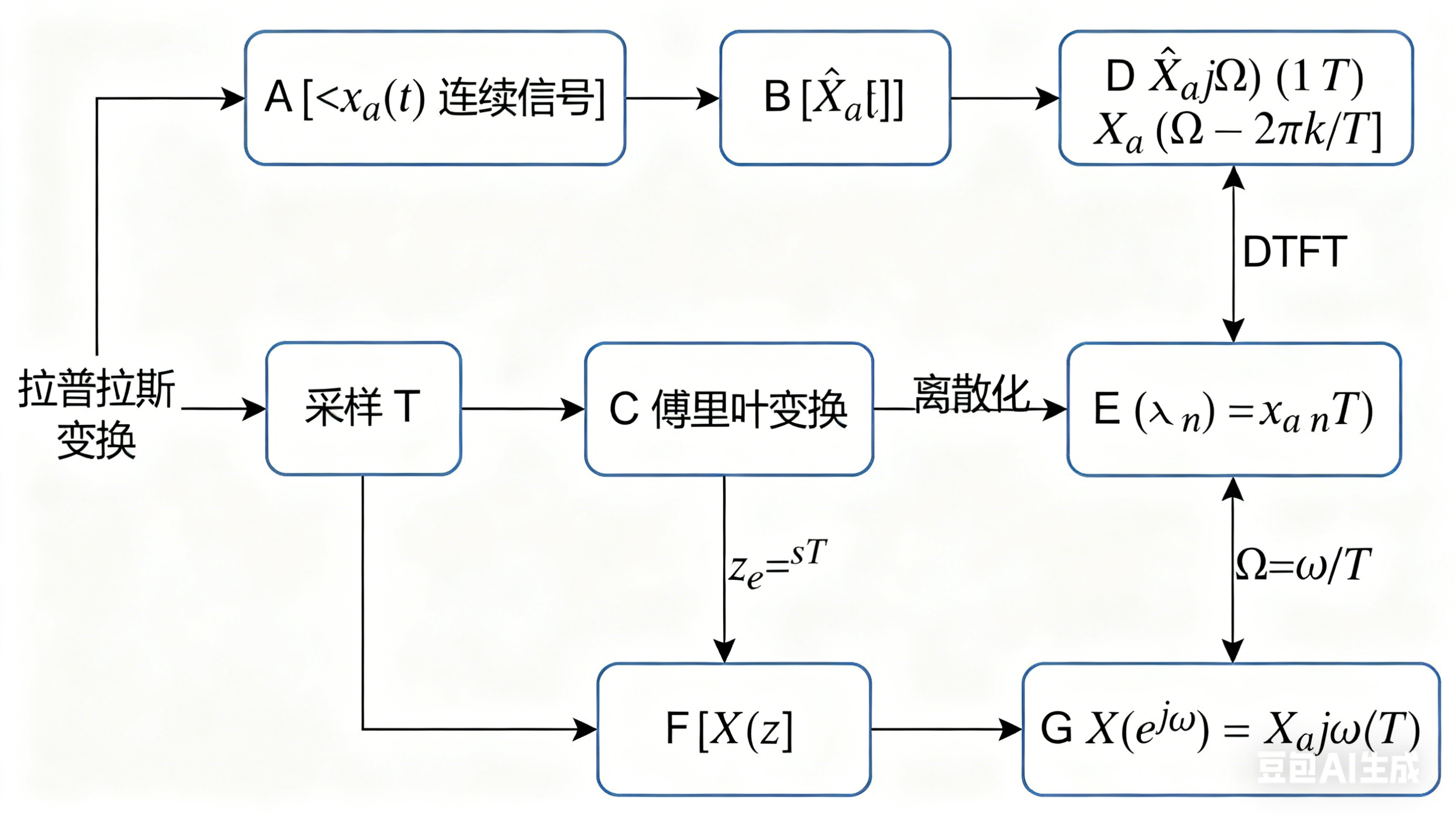
核心结论：

2.4 离散线性移不变系统的频域表征

2.4.1 LSI 系统的描述

线性移不变（LSI）系统是离散信号处理的核心模型，满足：

LSI 系统的 3 种描述方式：

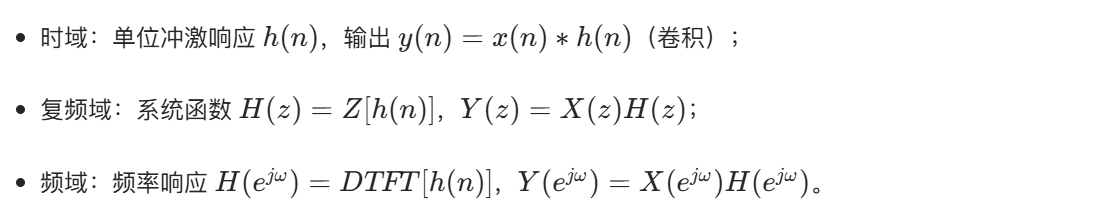
2.4.2 LSI 系统的因果、稳定条件

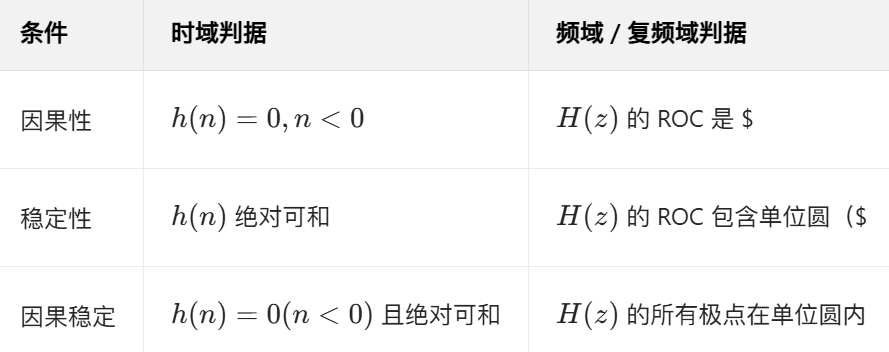
2.4.3 LSI 系统的频率响应 H(ejω) 及其特点

特点：

2.4.4 频率响应的几何确定法

核心规则：

  1. 幅频响应：零点到单位圆上点的距离乘积 / 极点到单位圆上点的距离乘积 × K；
  2. 相频响应：零点相位和 - 极点相位和；
  3. 极点靠近单位圆时，对应频率的幅频响应峰值越高（谐振）；
  4. 零点靠近单位圆时，对应频率的幅频响应谷值越低（抑制）。

MATLAB 实战：零极点对频率响应的影响（对比图）

复制代码 
% 2.4.4 频率响应的几何确定法 - 零极点影响对比
clc; clear; close all;

% 案例1：极点靠近单位圆（p=0.8），零点z=0
num1 = [1];    % 零点z=0
den1 = [1 -0.8];% 极点p=0.8
% 案例2：极点远离单位圆（p=0.4），零点z=0
num2 = [1];
den2 = [1 -0.4];

% 计算频率响应
[H1, omega1] = freqz(num1, den1, 1024);
[H2, omega2] = freqz(num2, den2, 1024);

% 绘制幅频响应对比
figure('Name','零极点对频率响应的影响');
subplot(2,1,1);
plot(omega1/pi, abs(H1), 'LineWidth', 1.5, 'DisplayName', '极点p=0.8');
hold on;
plot(omega2/pi, abs(H2), 'LineWidth', 1.5, 'DisplayName', '极点p=0.4');
xlabel('\omega/\pi'); ylabel('|H(e^{j\omega})|');
title('幅频响应对比（零点z=0）');
legend; grid on;

% 绘制零极点图
subplot(2,1,2);
pzmap(tf(num1, den1));  % 案例1零极点
hold on;
pzmap(tf(num2, den2));  % 案例2零极点
title('零极点图对比');
grid on;
axis equal;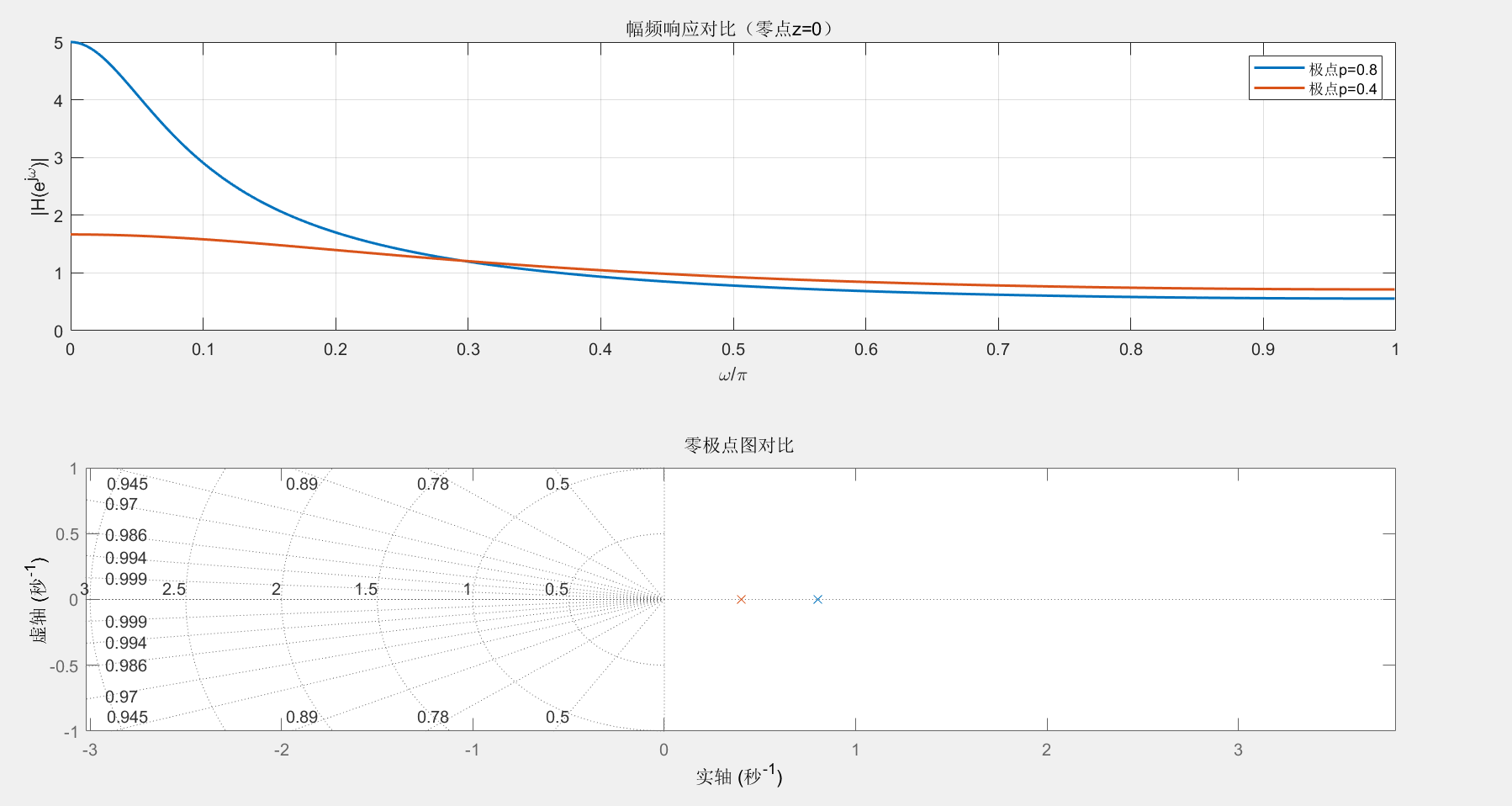

运行结果：极点越靠近单位圆（0.8 vs 0.4），幅频响应的峰值越高，直观验证了几何确定法的规则。

2.4.5 无限长单位冲激响应 (IIR) 系统与有限长单位冲激响应 (FIR) 系统

特性 IIR 系统 FIR 系统
单位冲激响应 h(n) 无限长 h(n) 有限长
系统函数 有理分式（有极点） 多项式（无极点，除 z=0）
稳定性 需保证极点在单位圆内 绝对稳定（h (n) 有限长）
相位特性 一般非线性相位 可设计成线性相位
实现复杂度 低（阶数少） 高（阶数高）

MATLAB 实战：IIR 与 FIR 滤波器对比（信号滤波效果）

复制代码 
% 2.4.5 IIR与FIR滤波器滤波效果对比
clc; clear; close all;

% 生成输入信号：100Hz+500Hz正弦混合信号（采样率1000Hz）
Fs = 1000;
t = 0:1/Fs:1-1/Fs;
x = sin(2*pi*100*t) + 0.5*sin(2*pi*500*t);

% 设计滤波器：低通，截止频率150Hz
% IIR滤波器（巴特沃斯）
[n_iir, wn_iir] = buttord(150/(Fs/2), 200/(Fs/2), 1, 40);
[b_iir, a_iir] = butter(n_iir, wn_iir);
% FIR滤波器（窗函数法）
n_fir = 100;  % 滤波器阶数
b_fir = fir1(n_fir, 150/(Fs/2), hamming(n_fir+1));
a_fir = 1;

% 滤波
y_iir = filtfilt(b_iir, a_iir, x);  % 零相位滤波
y_fir = filtfilt(b_fir, a_fir, x);

% 绘制滤波效果对比
figure('Name','IIR与FIR滤波器滤波效果对比');
subplot(3,1,1);
plot(t, x);
xlabel('t (s)'); ylabel('幅度');
title('原始信号（100Hz+500Hz）');
grid on;

subplot(3,1,2);
plot(t, y_iir);
xlabel('t (s)'); ylabel('幅度');
title('IIR滤波器输出（保留100Hz）');
grid on;

subplot(3,1,3);
plot(t, y_fir);
xlabel('t (s)'); ylabel('幅度');
title('FIR滤波器输出（保留100Hz）');
grid on;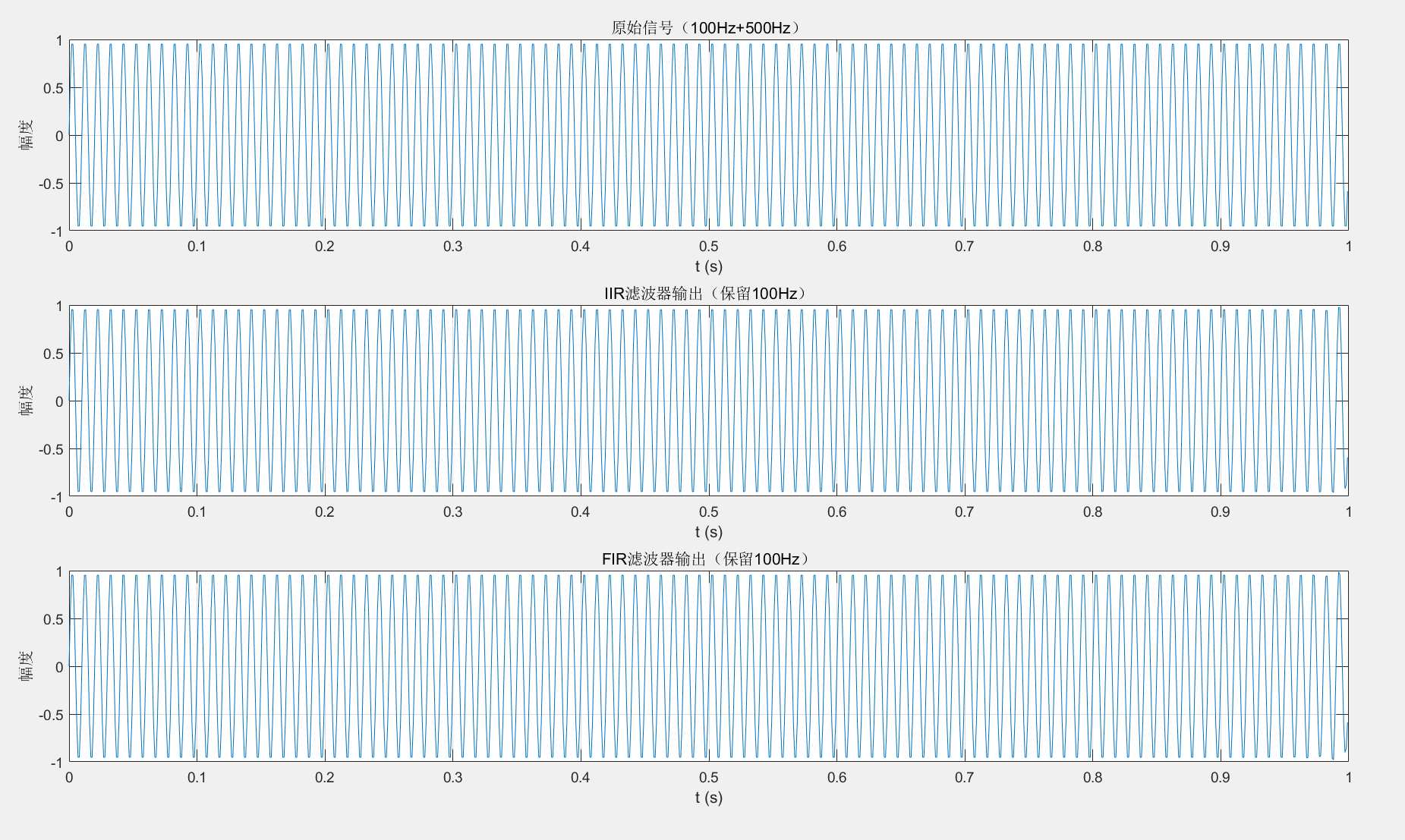

运行结果：两种滤波器都能滤除 500Hz 高频成分，保留 100Hz 低频成分；

FIR 滤波器相位更线性，输出无相位失真，

IIR 滤波器阶数更少但相位有轻微失真。

2.5 本章部分内容涉及的 MATLAB 函数及例题

核心函数总结

功能 MATLAB 函数 用途
z 变换 ztrans 符号计算序列的 z 变换
z 反变换 iztrans 符号计算 z 反变换
部分分式分解 residuez z 域部分分式分解（z 反变换）
差分方程求解 filter 求解线性常系数差分方程
DTFT 计算 freqz 计算频率响应（近似 DTFT）
零极点图 pzmap 绘制系统的零极点分布
滤波器设计 butter（IIR）、fir1（FIR） 设计 IIR/FIR 滤波器

综合例题：基于 z 变换和 DTFT 的信号分析

Matlab 复制代码 
% 2.5 综合例题：z变换+DTFT分析离散系统
% 功能：分析离散系统的零极点、冲激响应、频率响应，验证因果稳定性
% 说明：修复字符串拼接维度问题，增加鲁棒性校验，无隐形字符
clc; clear; close all;

%% 1. 定义系统：H(z) = (z+0.5)/(z^2 - 1.2z + 0.35)
num = [1 0.5];   % 分子多项式系数（z+0.5）
den = [1 -1.2 0.35];  % 分母多项式系数（z²-1.2z+0.35）

%% 2. 分析系统特性
% (2.1) 零极点与ROC分析（修复字符串拼接问题）
disp('========== 系统零极点与ROC分析 ==========');
z = roots(num);  % 零点
p = roots(den);  % 极点
% 统一转为行向量，避免列向量导致的字符串拼接错误
z = z(:)';       
p = p(:)';

% 格式化输出零极点（避免换行符）
disp(['零点：', num2str(z, '%.4f')]);  % 保留4位小数，行向量直接拼接
disp(['极点：', num2str(p, '%.4f')]);

% 校验极点是否在单位圆内（判断因果稳定性）
pole_abs = abs(p);
if all(pole_abs < 1)
    roc_desc = '|z| > max(|p|) = %.4f（因果稳定，所有极点在单位圆内）';
    roc_desc = sprintf(roc_desc, max(pole_abs));
else
    roc_desc = '|z| > max(|p|) = %.4f（因果但不稳定，存在单位圆外极点）';
    roc_desc = sprintf(roc_desc, max(pole_abs));
end
disp(['ROC：', roc_desc]);

% (2.2) 单位冲激响应h(n)
n = 0:29;                % 时域索引（前30点）
h = impz(num, den, length(n));  % 计算冲激响应

% (2.3) 频率响应H(e^jω)
[H, omega] = freqz(num, den, 1024);  % 高精度计算频率响应

%% 3. 绘制系统特性图（优化可视化）
figure('Name','综合例题：系统特性分析','Position',[100,100,900,700]);
% 子图1：零极点图（标注单位圆）
subplot(3,1,1);
pzmap(tf(num, den));  % 绘制零极点
hold on;
theta = linspace(0, 2*pi, 100);
plot(cos(theta), sin(theta), 'k--', 'LineWidth', 1);  % 绘制单位圆
title('系统零极点图（黑色虚线为单位圆）','FontSize',12,'FontWeight','bold');
grid on; axis equal;
hold off;

% 子图2：单位冲激响应
subplot(3,1,2);
stem(n, h, 'filled', 'Color', '#1f77b4', 'LineWidth', 1);
xlabel('n (时域索引)','FontSize',11);
ylabel('h(n)','FontSize',11);
title('单位冲激响应 h(n)','FontSize',12,'FontWeight','bold');
grid on; grid minor;
axis tight;

% 子图3：幅频响应（dB刻度）
subplot(3,1,3);
plot(omega/pi, 20*log10(abs(H)), 'LineWidth', 1.5, 'Color', '#ff7f0e');
xlabel('\omega/\pi (归一化频率)','FontSize',11);
ylabel('幅度 (dB)','FontSize',11);
title('系统幅频响应','FontSize',12,'FontWeight','bold');
grid on; grid minor;
axis tight;
% 标注峰值频率
[max_mag, max_idx] = max(20*log10(abs(H)));
max_omega = omega(max_idx)/pi;
hold on;
plot(max_omega, max_mag, 'ro', 'MarkerSize', 6, 'DisplayName', '峰值');
text(max_omega+0.05, max_mag, sprintf('(%.2fπ, %.1fdB)', max_omega, max_mag));
legend('幅频响应','峰值','Location','best');
hold off;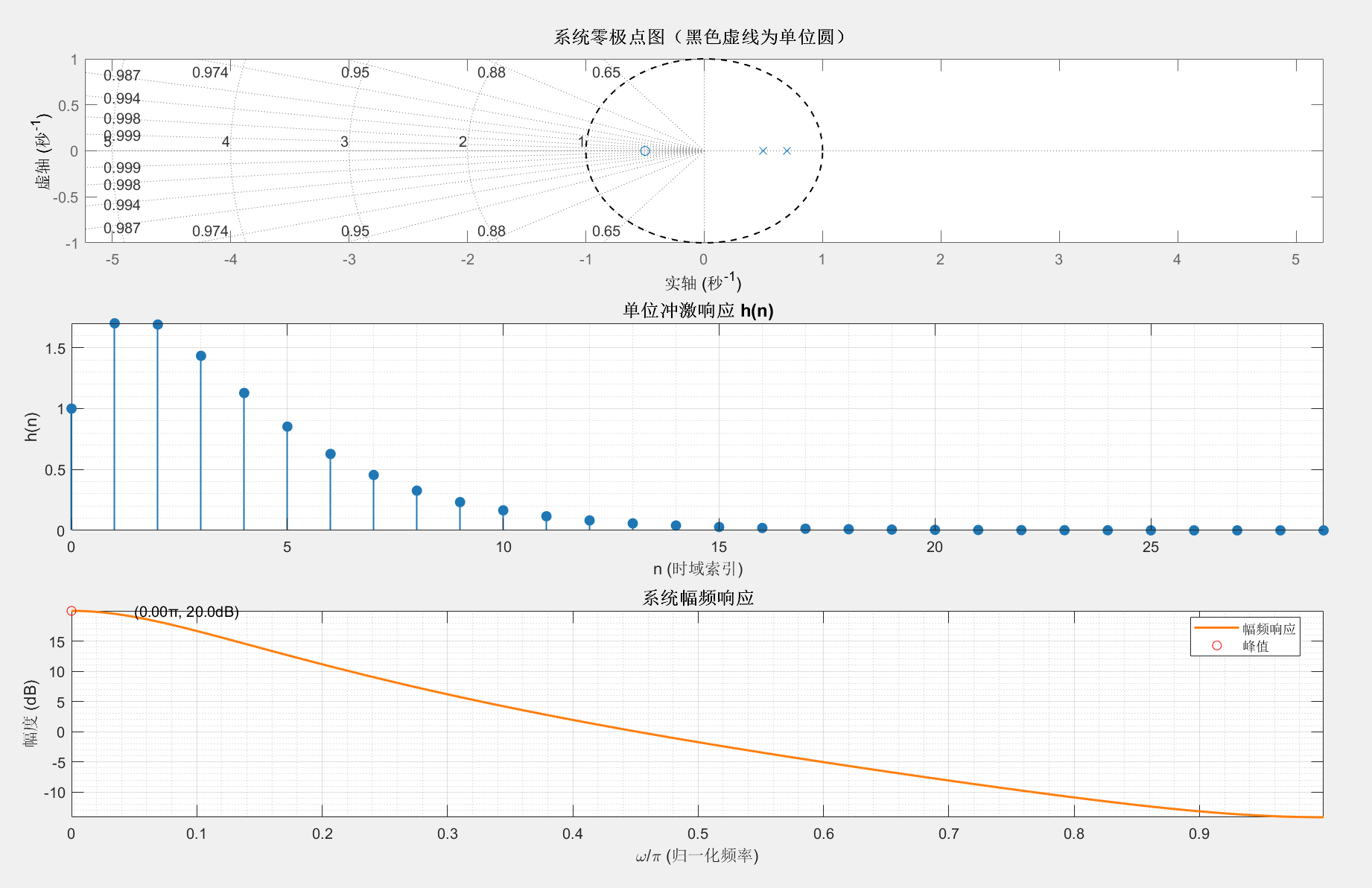

习题

总结

希望这篇内容能帮大家吃透 z 变换与 DTFT 的核心知识点，所有 MATLAB 代码均可直接运行，建议动手实操，结合对比图理解概念！如果有疑问，欢迎评论区交流～

相关推荐
hjs_deeplearning2 小时前
认知篇#15：ms-swift微调中gradient_accumulation_steps和warmup_ratio等参数的意义与设置
开发语言·人工智能·机器学习·swift·vlm
民乐团扒谱机2 小时前
【数模美赛=美术大赛？】O奖论文图片复刻——高级绘图matlab代码集锦，让你摆脱画图“一眼MATLAB”的痛苦！
前端·人工智能·matlab
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #146：LRU 缓存（双向链表、线程安全等多种实现方案详细解析）
算法·leetcode·lru·lru缓存·双向链表
武汉唯众智创2 小时前
全链路·工业级·强联动！物联网智慧城市实训平台，重塑职教实训新生态
人工智能·物联网·智慧城市·物联网实训平台·物联网智慧城市实训平台·智慧城市实训平台
凤希AI伴侣2 小时前
凤希AI伴侣的服饰探索与虚拟现实畅想-2026年1月26日
人工智能·凤希ai伴侣
程途拾光1582 小时前
中文用户常用在线流程图工具PC端高效制作各类业务流程图方法
大数据·论文阅读·人工智能·信息可视化·流程图·课程设计
胖墩会武术2 小时前
【PyTorch项目实战】FastSAM（快速分割一切）
人工智能·pytorch·python
浒畔居2 小时前
C++中的状态模式实战
开发语言·c++·算法
Coding茶水间2 小时前
基于深度学习的无人机检测系统演示与介绍(YOLOv12/v11/v8/v5模型+Pyqt5界面+训练代码+数据集)
人工智能·深度学习·yolo·目标检测·机器学习
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）08Open Code教程（四）| 高级配置与集成09Linux下V2Ray安装配置指南10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南