《数字信号处理》第 1 章 离散时间信号与系统

啊阿狸不会拉杆2026-01-28 8:13

前言

大家好！本文是《数字信号处理》入门核心章节 ------ 离散时间信号与系统的全解析，内容覆盖序列基础、线性移不变系统、差分方程、信号抽样四大核心模块，所有知识点均配套可直接运行的 MATLAB 代码 + 可视化对比图，力求用最通俗的语言讲清核心概念，帮大家夯实数信处理的入门基础。

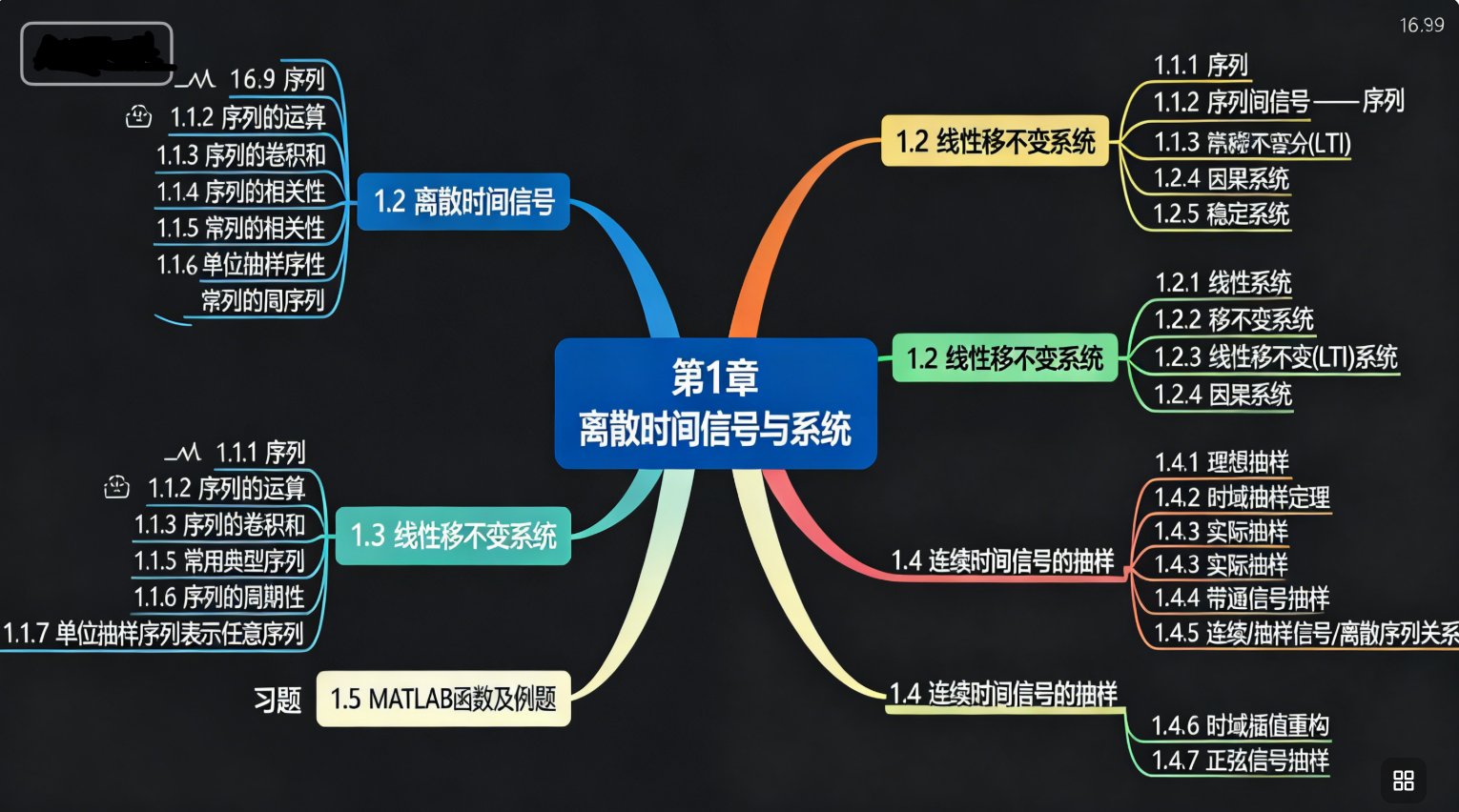
1.1 离散时间信号 ------ 序列

1.1.1 序列

序列是离散时间信号的数学表示，记为 x(n)，其中 n 为整数（仅在整数点有定义）。

MATLAB 代码（序列的定义与可视化）：

复制代码 
% 1.1.1 序列的定义与可视化
clc; clear; close all;

% 定义序列的自变量n（整数范围）
n = -5:5;
% 定义一个简单序列：单位阶跃序列u(n)
x = (n >= 0); % n>=0时为1，否则为0

% 绘制序列（离散信号用stem图）
figure('Color','w');
stem(n, x, 'filled', 'LineWidth',1);
xlabel('n (整数)'); ylabel('x(n)');
title('单位阶跃序列 u(n)');
grid on; % 显示网格，方便观察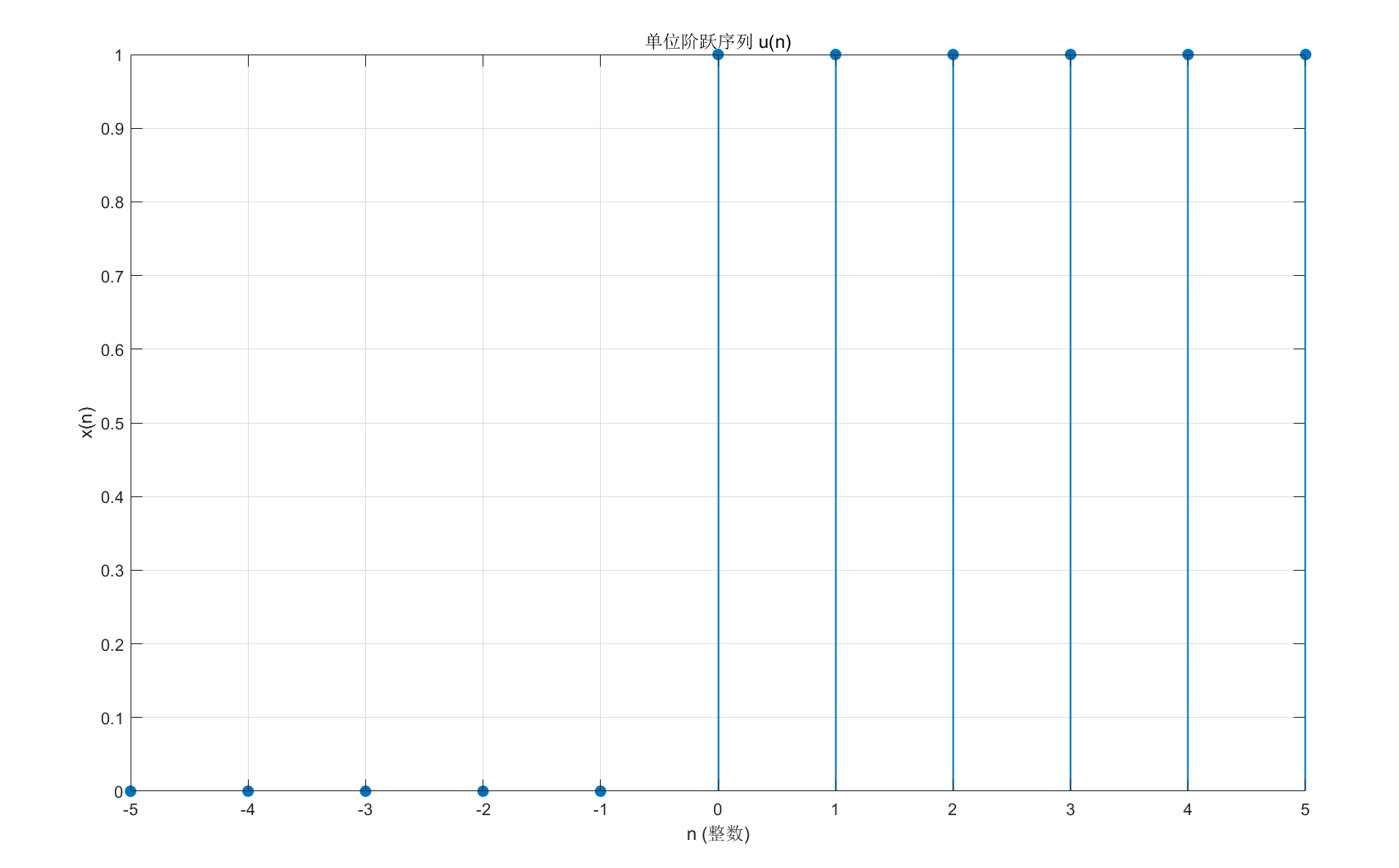

运行效果：生成 - 5 到 5 范围内的单位阶跃序列图，

n≥0 时序列值为 1，

n<0 时为 0，直观体现序列 "仅整数点有定义" 的特点。

1.1.2 序列的运算

序列的核心运算包括：移位、翻转、尺度变换、加减乘、累加 / 差分等。

MATLAB 代码（序列运算对比可视化）：

复制代码 
% 1.1.2 序列的运算（移位/翻转/加减乘）- 修复长度不匹配问题
clc; clear; close all;

% 原始序列定义
n = -4:6;          % 自变量n，长度11（-4,-3,-2,-1,0,1,2,3,4,5,6）
x1 = sin(0.2*pi*n);% 正弦序列1，长度11
x2 = 0.5*(n >= 0); % 幅值0.5的阶跃序列，长度11

% 1. 移位运算：统一保持序列长度与n一致（11个点），移位后补0
% 右移2位：x1(n-2)，即所有有效值向右移动2个位置，左侧补0
x1_shift_right = zeros(1, length(n)); % 初始化全0序列（长度11）
x1_shift_right(3:end) = x1(1:end-2);  % 从第3个位置开始填充原始x1的前9个点

% 左移1位：x1(n+1)，即所有有效值向左移动1个位置，右侧补0
x1_shift_left = zeros(1, length(n));  % 初始化全0序列（长度11）
x1_shift_left(1:end-1) = x1(2:end);   % 前10个位置填充原始x1的后10个点

% 2. 翻转运算：x1(-n)
n_flip = -flip(n);  % 翻转后的自变量：6:-1:-4
x1_flip = flip(x1); % 翻转后的序列值

% 3. 加减乘运算（长度天然匹配，无需修改）
x_add = x1 + x2;   % 相加，长度11
x_mul = x1 .* x2;  % 相乘（点乘），长度11

% 可视化对比（6个子图，统一窗口展示）
figure('Color','w');
% 原始序列
subplot(2,3,1); stem(n, x1, 'filled'); 
title('原始序列 x1(n)'); xlabel('n'); ylabel('幅值'); grid on;
% 右移2位
subplot(2,3,2); stem(n, x1_shift_right, 'filled'); 
title('x1(n-2) 右移2位'); xlabel('n'); ylabel('幅值'); grid on;
% 左移1位（修复后长度匹配）
subplot(2,3,3); stem(n, x1_shift_left, 'filled'); 
title('x1(n+1) 左移1位'); xlabel('n'); ylabel('幅值'); grid on;
% 翻转序列
subplot(2,3,4); stem(n_flip, x1_flip, 'filled'); 
title('x1(-n) 翻转'); xlabel('n'); ylabel('幅值'); grid on;
% 相加运算
subplot(2,3,5); stem(n, x_add, 'filled'); 
title('x1+x2 相加'); xlabel('n'); ylabel('幅值'); grid on;
% 相乘运算
subplot(2,3,6); stem(n, x_mul, 'filled'); 
title('x1.*x2 相乘'); xlabel('n'); ylabel('幅值'); grid on;

% 调整子图间距，避免重叠
sgtitle('序列运算对比图');
set(gcf, 'Position', [100, 100, 1000, 600]); % 设置窗口大小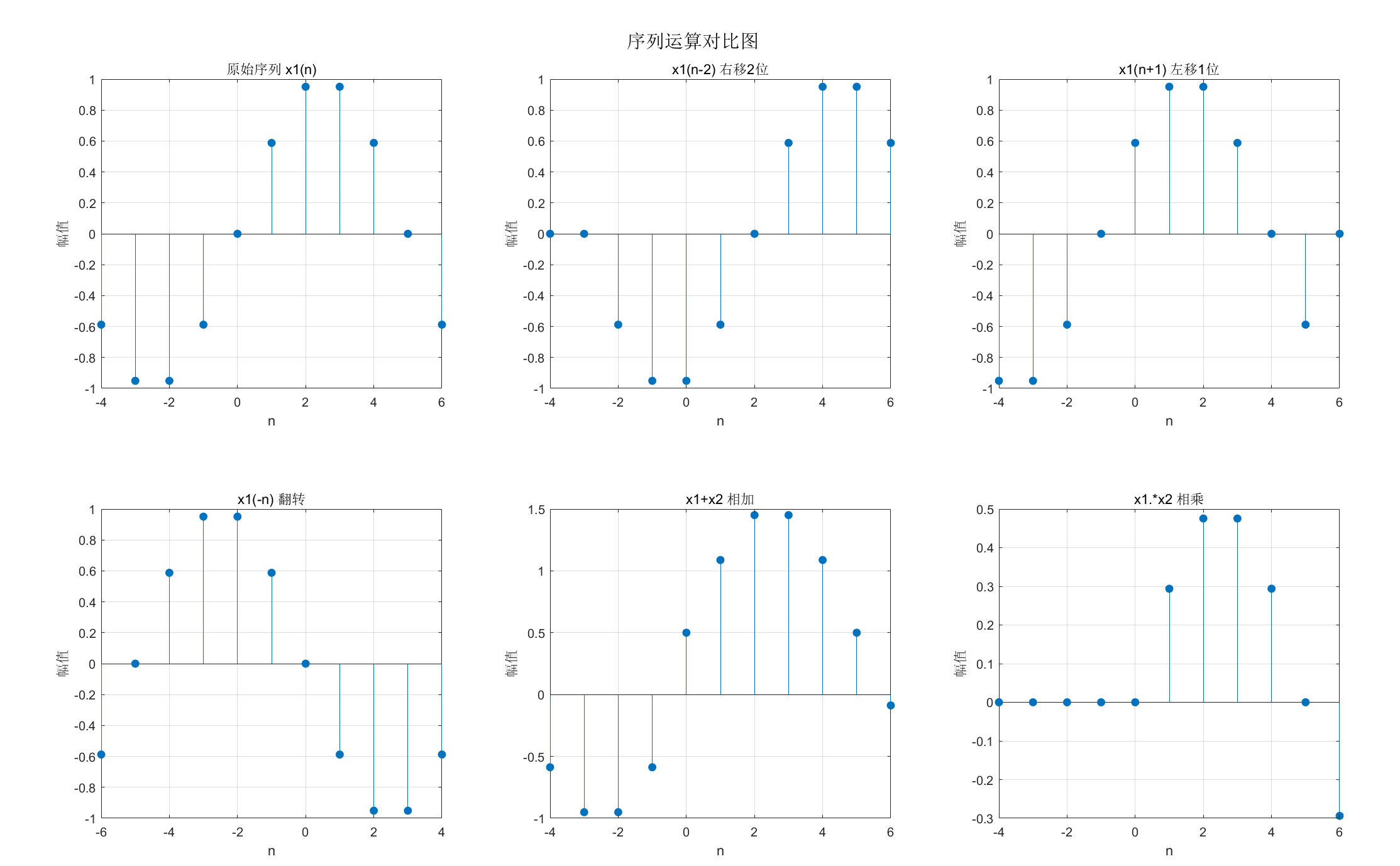

运行效果：同一窗口显示原始序列、移位、翻转、加减乘的 6 张对比图，清晰看到不同运算对序列的影响。

1.1.3 序列的卷积和

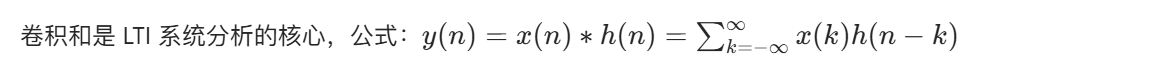
MATLAB 代码（卷积和计算 + 可视化）：

复制代码 
% 1.1.3 序列的卷积和计算与可视化
clc; clear; close all;

% 定义输入序列x(n)和系统单位抽样响应h(n)
n_x = 0:4; x = [1,2,3,2,1]; % 输入序列
n_h = 0:2; h = [1,1,1];     % 单位抽样响应

% 方法1：手动计算卷积和（理解原理）
len_y = length(x) + length(h) - 1; % 卷积结果长度
y_manual = zeros(1, len_y);
for n = 1:len_y
    sum_val = 0;
    for k = 1:length(x)
        m = n - k + 1; % 对应h的索引
        if m >= 1 && m <= length(h)
            sum_val = sum_val + x(k)*h(m);
        end
    end
    y_manual(n) = sum_val;
end

% 方法2：调用MATLAB内置函数conv（高效）
y_conv = conv(x, h);

% 卷积结果的自变量n_y
n_y = n_x(1) + n_h(1) : n_x(end) + n_h(end);

% 可视化对比（原始序列+两种方法卷积结果）
figure('Color','w');
subplot(3,1,1); stem(n_x, x, 'filled'); title('输入序列 x(n)'); xlabel('n'); ylabel('幅值'); grid on;
subplot(3,1,2); stem(n_h, h, 'filled'); title('单位抽样响应 h(n)'); xlabel('n'); ylabel('幅值'); grid on;
subplot(3,1,3); stem(n_y, y_conv, 'filled'); 
hold on; stem(n_y, y_manual, 'r*', 'MarkerSize',8); % 手动结果用红色星号标注
title('卷积和结果 y(n)=x(n)*h(n)'); 
xlabel('n'); ylabel('幅值'); 
legend('conv函数计算','手动计算','Location','best');
grid on;

sgtitle('序列卷积和对比');
set(gcf, 'Position', [100, 100, 800, 600]);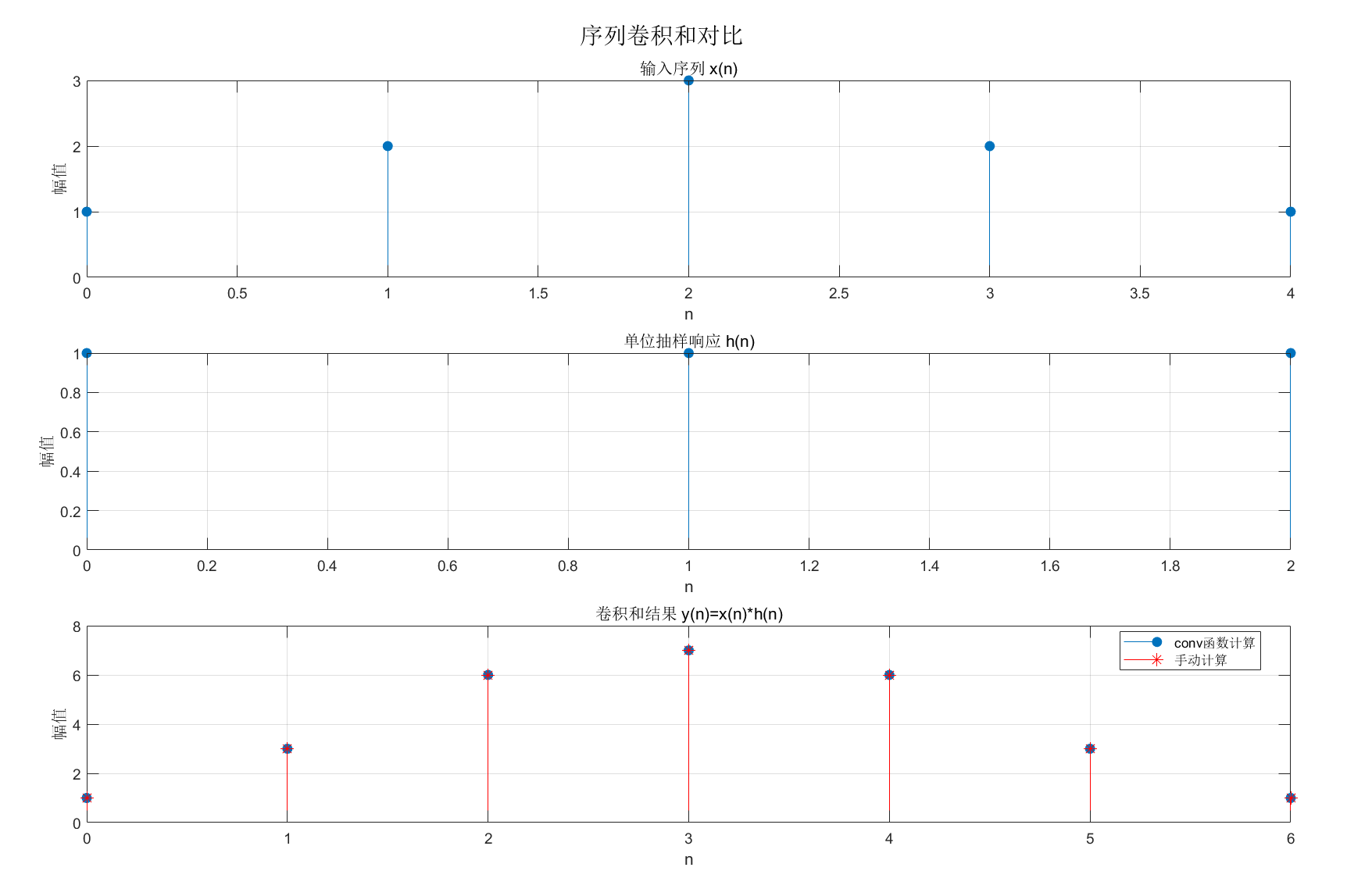

运行效果：显示输入序列、单位抽样响应、卷积结果（两种方法结果完全一致），验证卷积和的计算逻辑。

1.1.4 序列的相关性

相关性用于衡量两个序列的相似程度，分为自相关（自身）和互相关（两个序列），公式：

MATLAB 代码（相关性计算 + 可视化）：

复制代码 
% 1.1.4 序列的相关性（自相关+互相关）
clc; clear; close all;

% 定义原始序列
n = 0:10;
x = sin(0.2*pi*n) + 0.1*randn(1, length(n)); % 带噪声的正弦序列
y = cos(0.2*pi*n);                           % 余弦序列

% 计算自相关和互相关（使用xcorr函数）
[r_xx, lag_xx] = xcorr(x, 'biased'); % 自相关（有偏估计）
[r_xy, lag_xy] = xcorr(x, y, 'biased'); % 互相关（有偏估计）

% 可视化对比
figure('Color','w');
subplot(2,2,1); stem(n, x, 'filled'); title('原始序列 x(n)'); xlabel('n'); ylabel('幅值'); grid on;
subplot(2,2,2); stem(n, y, 'filled'); title('原始序列 y(n)'); xlabel('n'); ylabel('幅值'); grid on;
subplot(2,2,3); stem(lag_xx, r_xx, 'filled'); title('x(n)的自相关 r_xx(m)'); xlabel('延迟m'); ylabel('相关值'); grid on;
subplot(2,2,4); stem(lag_xy, r_xy, 'filled'); title('x(n)与y(n)的互相关 r_xy(m)'); xlabel('延迟m'); ylabel('相关值'); grid on;

sgtitle('序列相关性对比');
set(gcf, 'Position', [100, 100, 900, 600]);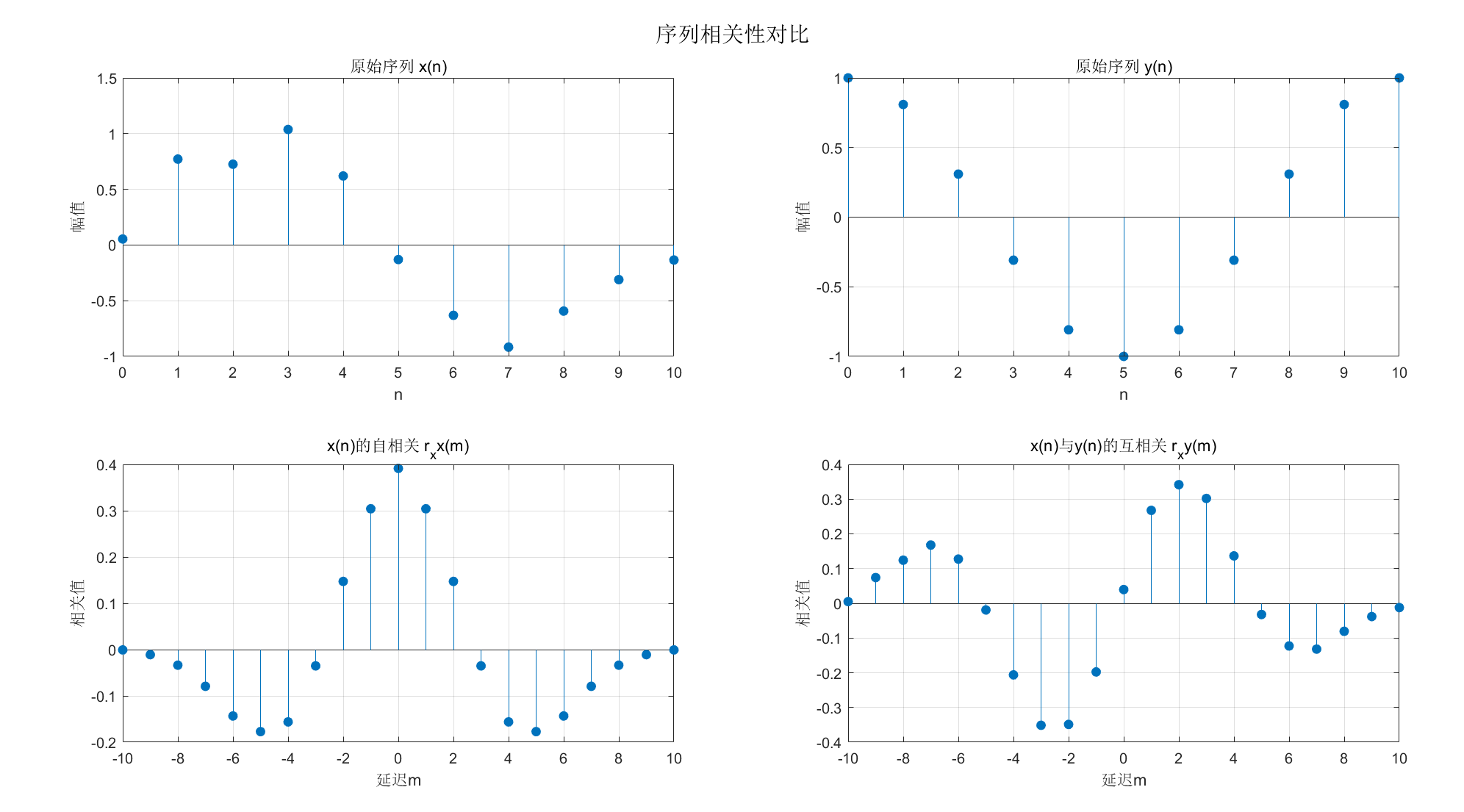

运行效果：同一窗口显示原始序列、自相关、互相关结果，可观察到自相关在延迟 0 处峰值最大，互相关峰值位置对应两序列的相位差。

1.1.5 几种常用的典型序列

常用典型序列：单位抽样序列δ(n)、单位阶跃序列u(n)、矩形序列RN​(n)、正弦序列、指数序列等。

MATLAB 代码（典型序列可视化对比）：

复制代码 
% 1.1.5 常用典型序列可视化
clc; clear; close all;

% 定义自变量范围（n从-5到10，共16个点）
n = -5:10; 

% 1. 单位抽样序列 δ(n)：仅n=0时为1，其余为0
delta = (n == 0); 

% 2. 单位阶跃序列 u(n)：n≥0时为1，n<0时为0
u = (n >= 0);

% 3. 矩形序列 R_5(n)：n∈[0,4]时为1，其余为0
R5 = (n >= 0) & (n < 5);

% 4. 正弦序列：sin(0.3πn)
sin_seq = sin(0.3*pi*n);

% 5. 衰减指数序列：(0.8)^n * u(n)（n<0时为0，n≥0时指数衰减）
exp_seq = (0.8).^n .* u;

% 可视化（5个子图，3行2列布局，最后一列空出）
figure('Color','w'); % 设置背景为白色，避免默认灰色
subplot(3,2,1); 
stem(n, delta, 'filled', 'Color', '#0072BD'); % 蓝色填充
title('单位抽样序列 δ(n)'); 
xlabel('n'); ylabel('幅值'); 
grid on; % 显示网格，方便观察

subplot(3,2,2); 
stem(n, u, 'filled', 'Color', '#D95319'); % 橙色填充
title('单位阶跃序列 u(n)'); 
xlabel('n'); ylabel('幅值'); 
grid on;

subplot(3,2,3); 
stem(n, R5, 'filled', 'Color', '#EDB120'); % 黄色填充
title('矩形序列 R_5(n)'); 
xlabel('n'); ylabel('幅值'); 
grid on;

subplot(3,2,4); 
stem(n, sin_seq, 'filled', 'Color', '#7E2F8E'); % 紫色填充
title('正弦序列 sin(0.3πn)'); 
xlabel('n'); ylabel('幅值'); 
grid on;

subplot(3,2,5); 
stem(n, exp_seq, 'filled', 'Color', '#77AC30'); % 绿色填充
title('衰减指数序列 (0.8)^n u(n)'); 
xlabel('n'); ylabel('幅值'); 
grid on;

% 设置总标题，调整子图间距和窗口大小
sgtitle('常用典型序列对比', 'FontSize', 14);
set(gcf, 'Position', [100, 100, 900, 700]); % 窗口位置：(100,100)，大小：900x700
% 调整子图间距，避免标题/标签重叠
set(gca, 'Position', [0.1, 0.1, 0.8, 0.8]);
subplot(3,2,6); % 空出最后一个子图，避免布局混乱
axis off; % 隐藏空图的坐标轴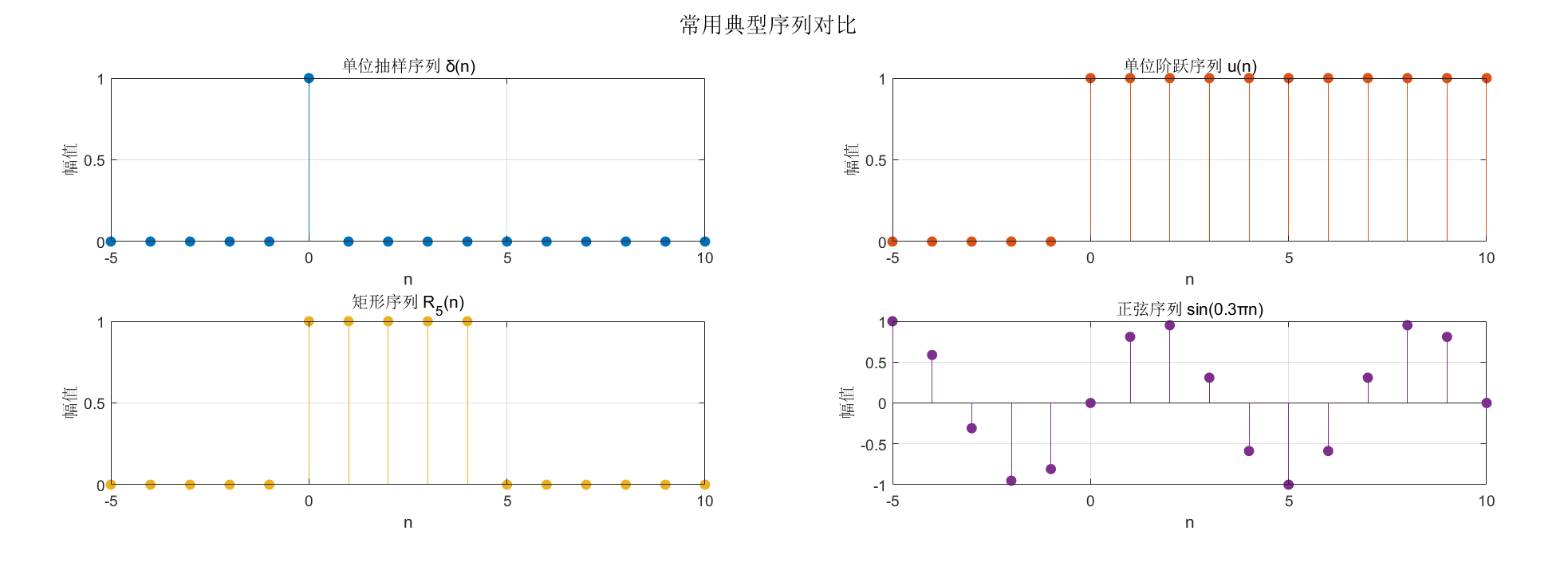

运行效果：直观展示 5 种典型序列的形态，理解各自的定义和特征。

1.1.6 序列的周期性

MATLAB 代码（周期序列判断 + 可视化）：

复制代码 
% 1.1.6 序列的周期性验证
clc; clear; close all;

n = 0:20;
% 例1：周期序列（ω0=2π/5，周期N=5）
sin_period = sin(2*pi/5 * n);
% 例2：非周期序列（ω0=0.3π，2π/0.3π=20/3 非整数）
sin_nonperiod = sin(0.3*pi * n);

% 可视化对比
figure('Color','w');
subplot(2,1,1); stem(n, sin_period, 'filled'); 
title('周期正弦序列 sin(2π/5 * n)（周期N=5）'); 
xlabel('n'); ylabel('幅值'); grid on;
% 标注周期（每5个点画一条竖线）
for k = 0:5:20
    xline(k, 'r--', 'LineWidth',0.8);
end

subplot(2,1,2); stem(n, sin_nonperiod, 'filled'); 
title('非周期正弦序列 sin(0.3π * n)'); 
xlabel('n'); ylabel('幅值'); grid on;

set(gcf, 'Position', [100, 100, 800, 600]);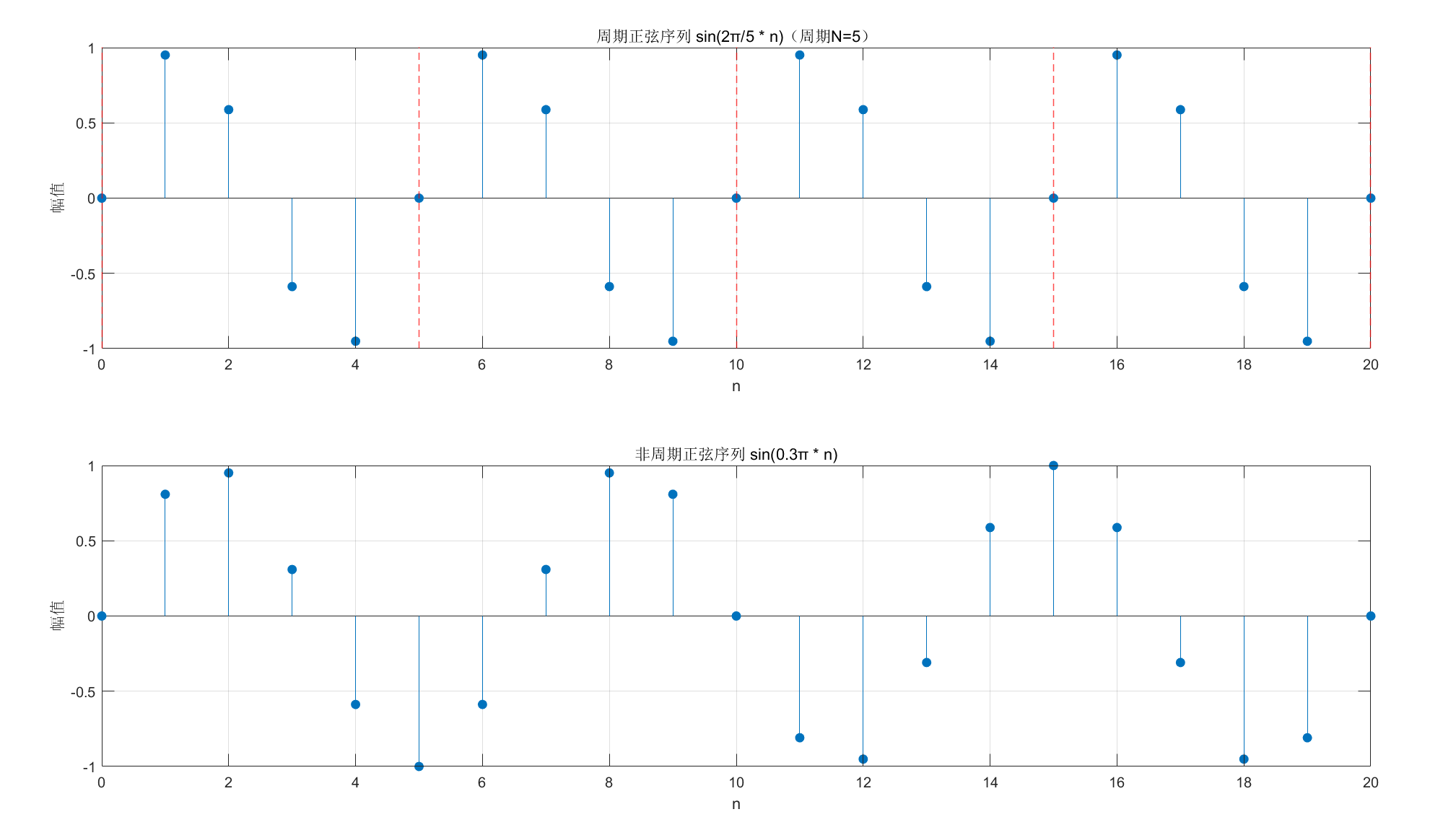

运行效果：对比周期与非周期正弦序列，周期序列每 5 个点重复，非周期序列无重复规律。

1.1.7 用单位抽样序列表示任意序列

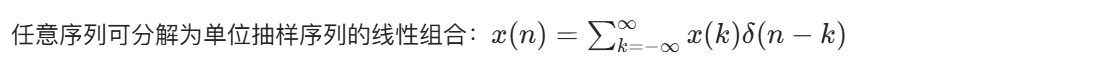
MATLAB 代码（序列分解验证）：

Matlab 复制代码 
% 1.1.7 用单位抽样序列表示任意序列（修复三目运算符报错）
clc; clear; close all;

% 定义任意序列的自变量和序列值
n = -3:5;          % 自变量范围：-3,-2,-1,0,1,2,3,4,5（共9个点）
x = [2, -1, 0, 3, 1, -2, 4, 0, 1]; % 对应n的序列值

% 分解为单位抽样序列的线性组合（核心逻辑）
x_recon = zeros(1, length(n)); % 初始化重构序列为全0（长度与n一致）
for k = 1:length(n)
    % 生成移位后的单位抽样序列 δ(n - n(k))：仅当n等于n(k)时为1，其余为0
    delta_k = (n == n(k)); 
    % 线性组合：x(k) * δ(n - n(k))，累加到重构序列中
    x_recon = x_recon + x(k) * delta_k; 
end

% 可视化对比（原始序列 vs 重构序列）
figure('Color','w'); % 设置背景为白色
% 原始序列
subplot(2,1,1); 
stem(n, x, 'filled', 'Color', '#0072BD'); % 蓝色填充
title('原始序列 x(n)'); 
xlabel('n'); ylabel('幅值'); 
grid on; % 显示网格，方便观察

% 重构序列
subplot(2,1,2); 
stem(n, x_recon, 'filled', 'Color', '#D95319'); % 橙色填充
title('单位抽样序列重构的序列'); 
xlabel('n'); ylabel('幅值'); 
grid on;

% 验证重构是否完全一致（替换MATLAB不支持的三目运算符）
if isequal(x, x_recon)
    fprintf('原始序列与重构序列是否一致：是\n');
else
    fprintf('原始序列与重构序列是否一致：否\n');
end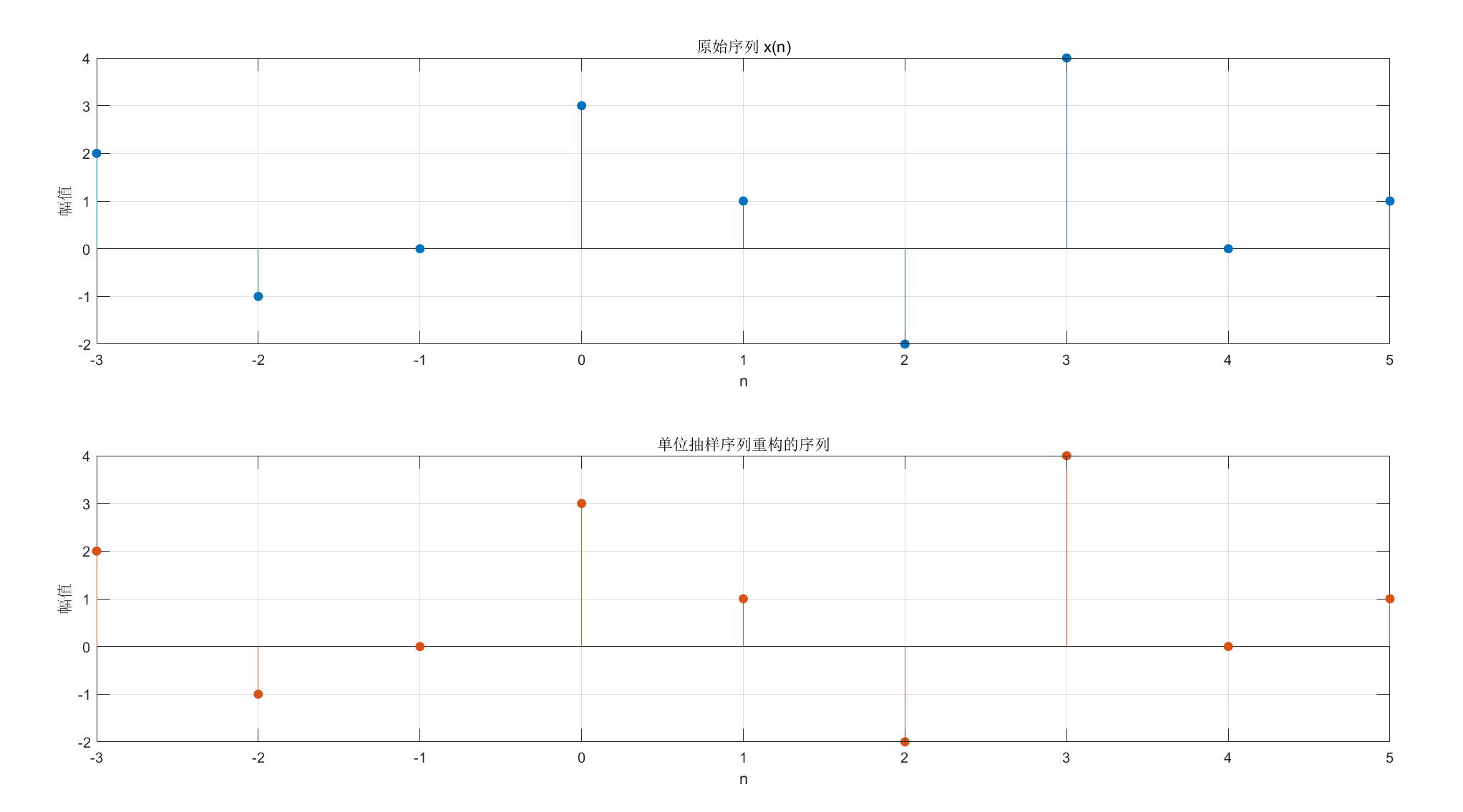

运行效果：原始序列与重构序列完全重合，验证分解公式的正确性。

1.2 线性移不变系统

1.2.1-1.2.3 线性、移不变、LTI 系统

核心定义：

  • 线性系统：满足叠加性 + 齐次性；
  • 移不变系统：输入移位，输出同移位（x(n)→y(n)，则x(n−k)→y(n−k)）；
  • LTI 系统：同时满足线性 + 移不变，可用卷积和描述输入输出关系。

MATLAB 代码（LTI 系统验证）：

Matlab 复制代码 
% 1.2 线性移不变(LTI)系统验证（修复隐形字符+语法问题）
clc; clear; close all;

% 定义LTI系统的单位抽样响应：h(n) = (0.5)^n * u(n)（衰减指数响应）
h = @(n) (0.5).^n .* (n >= 0); 

% 定义两个输入序列的自变量范围
n = 0:8;
x1 = sin(0.2*pi*n);          % 正弦输入序列
x2 = 2 * ones(1, length(n)); % 常数输入序列
a = 2; b = 3;                % 线性组合系数

% ========== 线性性验证 ==========
% 方法1：先线性组合输入，再通过LTI系统
x_comb = a*x1 + b*x2;
y_comb = conv(x_comb, h(n)); % 卷积计算系统输出

% 方法2：先让各输入通过系统，再线性组合输出
y1 = conv(x1, h(n));
y2 = conv(x2, h(n));
y_lin = a*y1 + b*y2;

% ========== 移不变性验证 ==========
% 输入序列右移1位（补0，保持长度与原x1一致）
x1_shift = [0, x1(1:end-1)]; 
% 移位输入的系统输出
y1_shift = conv(x1_shift, h(n)); 
% 原输出y1右移1位（补0，保持长度与y1_shift一致）
y_comb_shift = [0, y1(1:end-1), zeros(1, length(y1_shift)-length(y1))]; 

% ========== 可视化验证结果 ==========
figure('Color','w'); % 设置背景为白色

% 1. 线性性验证子图
subplot(2,1,1); 
% 先组合后系统的输出（蓝色填充）
stem(0:length(y_comb)-1, y_comb, 'b-', 'filled'); hold on;
% 先系统后组合的输出（红色星号标注）
stem(0:length(y_lin)-1, y_lin, 'r*', 'MarkerSize',6);
title('线性性验证：LTI系统满足叠加性');
xlabel('n'); ylabel('输出幅值');
legend('先组合后系统','先系统后组合','Location','best');
grid on;

% 2. 移不变性验证子图
subplot(2,1,2);
% 移位输入的输出（蓝色填充）
stem(0:length(y1_shift)-1, y1_shift, 'b-', 'filled'); hold on;
% 原输出移位结果（红色星号标注）
stem(0:length(y_comb_shift)-1, y_comb_shift, 'r*', 'MarkerSize',6);
title('移不变性验证：输入移位→输出同移位');
xlabel('n'); ylabel('输出幅值');
legend('移位输入的输出','原输出移位','Location','best');
grid on;

% 调整窗口大小，避免内容重叠
set(gcf, 'Position', [100, 100, 800, 600]);

% ========== 数值验证（替换不支持的三目运算符） ==========
% 线性性验证：四舍五入到4位小数后比较
if isequal(round(y_comb,4), round(y_lin,4))
    fprintf('线性性验证：结果一致 → LTI系统满足线性性\n');
else
    fprintf('线性性验证：结果不一致 → 系统不满足线性性\n');
end

% 移不变性验证：四舍五入到4位小数后比较
if isequal(round(y1_shift,4), round(y_comb_shift,4))
    fprintf('移不变性验证：结果一致 → LTI系统满足移不变性\n');
else
    fprintf('移不变性验证：结果不一致 → 系统不满足移不变性\n');
end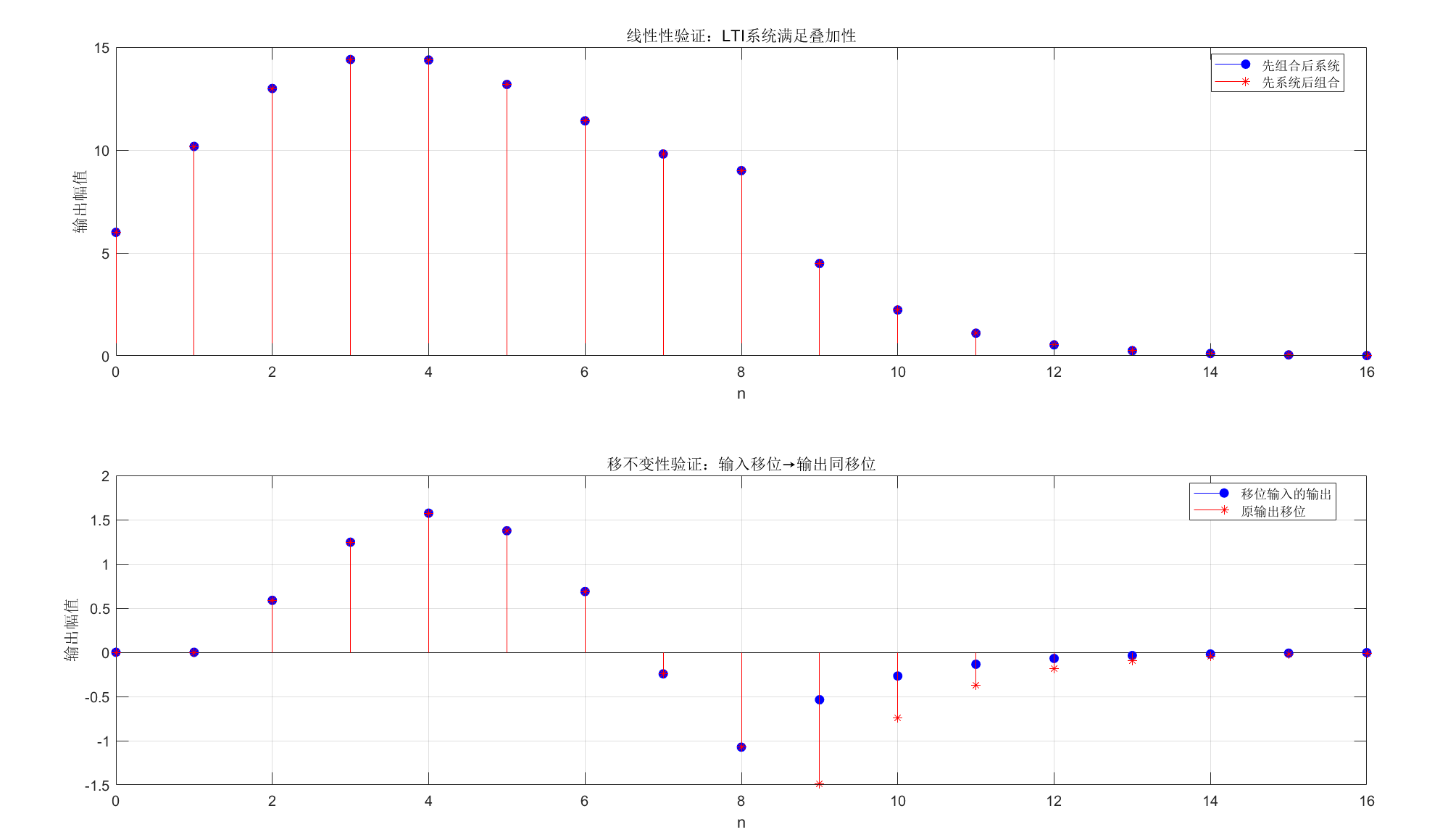

运行效果：线性性验证中两条曲线完全重合，移不变性验证中移位输入的输出与原输出移位结果一致，验证 LTI 系统特性。

1.2.4 因果系统

因果系统：输出仅由当前及过去的输入决定（n<0时，单位抽样响应h(n)=0）。

1.2.5 稳定系统

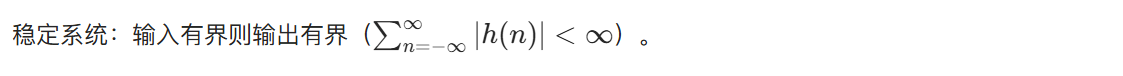
MATLAB 代码（因果 + 稳定系统判断）：

复制代码 
% 1.2.4-1.2.5 因果/稳定系统判断
clc; clear; close all;

n = -5:10;
% 例1：因果稳定系统（h(n)=(0.5)^n u(n)）
h1 = (0.5).^n .* (n >= 0);
% 例2：非因果系统（h(n)=(0.5)^n u(n+2)，n<0时有值）
h2 = (0.5).^n .* (n >= -2);
% 例3：不稳定系统（h(n)=2^n u(n)，求和无界）
h3 = 2.^n .* (n >= 0);

% 计算绝对和（稳定判断）
sum_h1 = sum(abs(h1));
sum_h3 = sum(abs(h3)); % 数值上会显示很大的数

% 可视化
figure('Color','w');
subplot(3,1,1); stem(n, h1, 'filled'); 
title(sprintf('因果稳定系统 h1(n)=(0.5)^n u(n)，绝对和=%.2f', sum_h1)); 
xlabel('n'); ylabel('h(n)'); grid on;
xline(0, 'r--', 'LineWidth',0.8); % 标注n=0，因果性分界

subplot(3,1,2); stem(n, h2, 'filled'); 
title('非因果系统 h2(n)=(0.5)^n u(n+2)（n<0时有值）'); 
xlabel('n'); ylabel('h(n)'); grid on;
xline(0, 'r--', 'LineWidth',0.8);

subplot(3,1,3); stem(n, h3, 'filled'); 
title(sprintf('不稳定系统 h3(n)=2^n u(n)，绝对和=%.2f', sum_h3)); 
xlabel('n'); ylabel('h(n)'); grid on;
xline(0, 'r--', 'LineWidth',0.8);

set(gcf, 'Position', [100, 100, 800, 700]);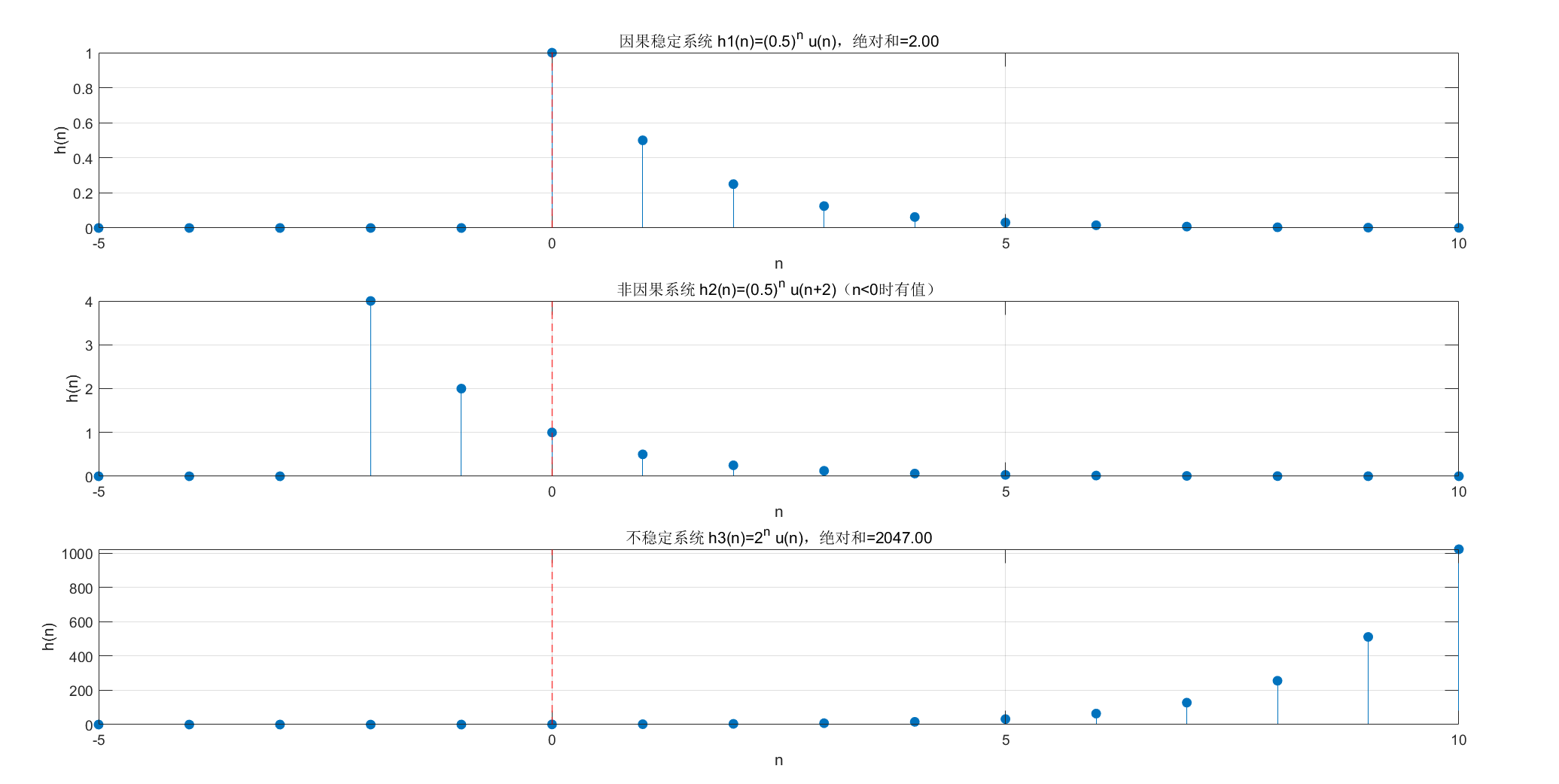

运行效果：清晰区分因果 / 非因果、稳定 / 不稳定系统的单位抽样响应形态，因果系统 n<0 时 h (n)=0，稳定系统绝对和有限。

1.3 常系数线性差分方程

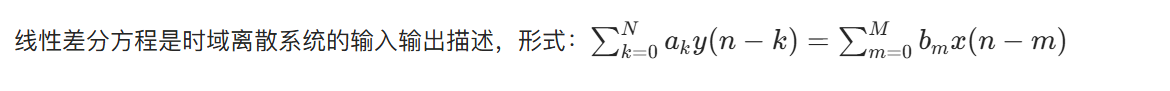
MATLAB 代码（差分方程求解）：

复制代码 
% 1.3 常系数线性差分方程求解
clc; clear; close all;

% 定义差分方程：y(n) - 0.7y(n-1) + 0.1y(n-2) = x(n) + 0.5x(n-1)
a = [1, -0.7, 0.1]; % 输出系数
b = [1, 0.5];       % 输入系数

% 定义输入序列（单位阶跃序列）
n = 0:20;
x = ones(1, length(n));

% 求解差分方程（零初始条件）
y = filter(b, a, x);

% 可视化输出
figure('Color','w');
stem(n, y, 'filled');
title('差分方程输出 y(n) - 0.7y(n-1) + 0.1y(n-2) = x(n) + 0.5x(n-1)');
xlabel('n'); ylabel('y(n)');
grid on;
set(gcf, 'Position', [100, 100, 800, 500]);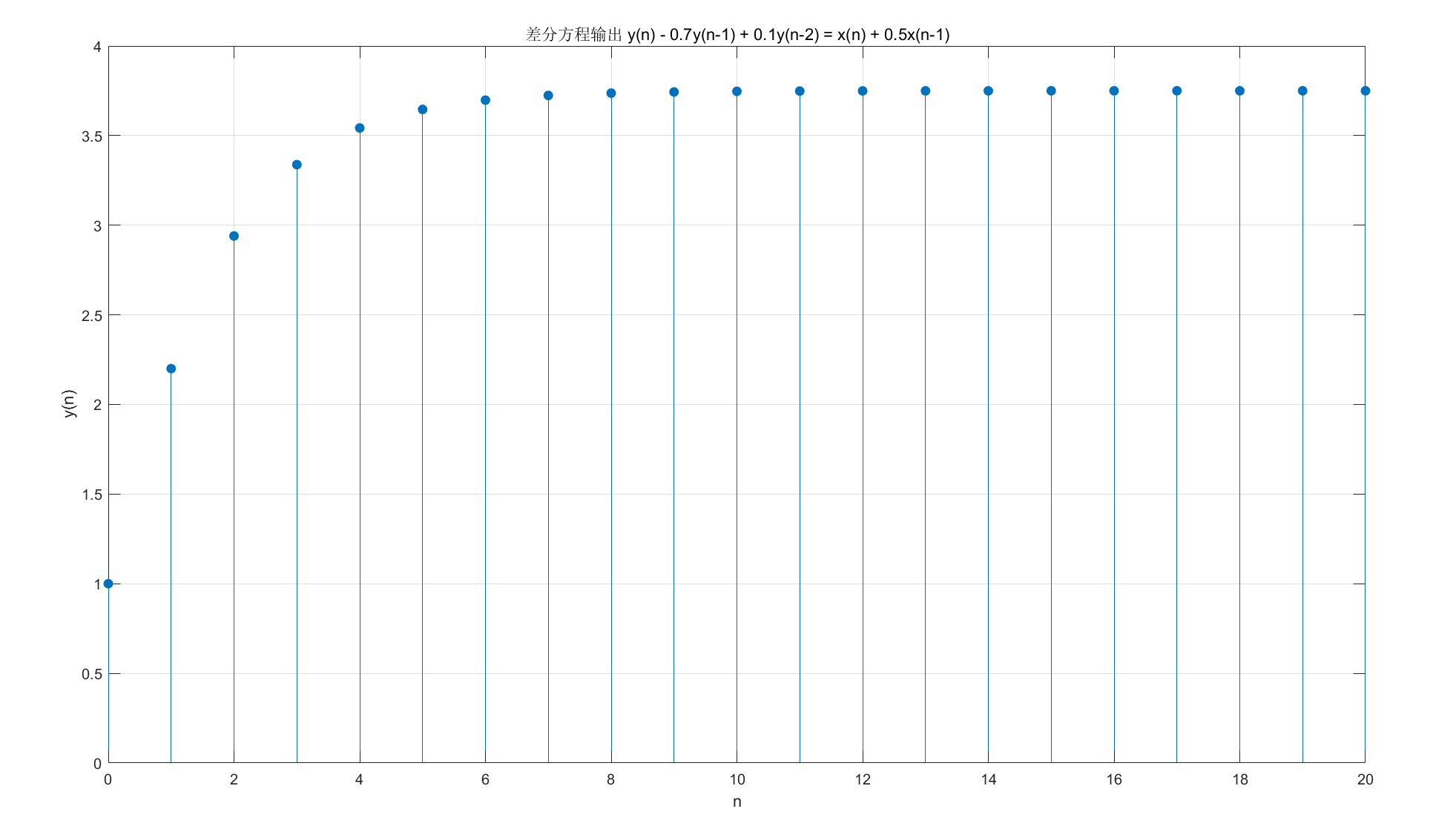

运行效果：输出差分方程的时域响应，直观看到系统的输出变化规律。

1.4 连续时间信号的抽样

1.4.1-1.4.7 抽样核心知识点

核心逻辑：

MATLAB 代码（抽样 + 重构 + 混叠对比）：

Matlab 复制代码 
% 1.4 连续信号的抽样与重构（含混叠对比）- 修复矩阵维度不匹配+清理隐形字符
clc; clear; close all;

% ========== 1. 定义连续信号 ==========
% 连续信号：x_a(t) = sin(2π*10t) + cos(2π*20t)，最高频率f_max=20Hz
f1 = 10; f2 = 20; % 信号分量频率
fs1 = 50;         % 抽样频率50Hz（>2*f_max=40Hz，满足奈奎斯特抽样定理）
fs2 = 30;         % 抽样频率30Hz（<40Hz，不满足定理，产生混叠）

% 高精度连续时间轴（步长0.001s，保证连续信号平滑）
t_cont = 0:0.001:1; 
x_cont = sin(2*pi*f1*t_cont) + cos(2*pi*f2*t_cont);

% ========== 2. 对连续信号进行抽样 ==========
% 抽样1：满足定理（fs1=50Hz）
Ts1 = 1/fs1; t1 = 0:Ts1:1; % 抽样时间点（行向量，长度=51）
x1 = sin(2*pi*f1*t1) + cos(2*pi*f2*t1); % 抽样值（行向量，长度=51）

% 抽样2：不满足定理（fs2=30Hz）
Ts2 = 1/fs2; t2 = 0:Ts2:1; % 抽样时间点（行向量，长度=31）
x2 = sin(2*pi*f1*t2) + cos(2*pi*f2*t2); % 抽样值（行向量，长度=31）

% ========== 3. 插值重构（修复维度匹配问题） ==========
t_recon = t_cont;
x_recon1 = zeros(1, length(t_recon)); % 初始化重构信号1
x_recon2 = zeros(1, length(t_recon)); % 初始化重构信号2

% 方法1：回归高效的逐点计算（维度匹配，逻辑直观）
for i = 1:length(t_recon)
    % 逐元素相乘后求和（sinc插值核心公式）
    x_recon1(i) = sum(x1 .* sinc(fs1 * (t_recon(i) - t1)));
    x_recon2(i) = sum(x2 .* sinc(fs2 * (t_recon(i) - t2)));
end

% ========== 4. 可视化对比（原始+满足定理+混叠） ==========
figure('Color','w'); % 背景设为白色

% 子图1：原始连续信号
subplot(3,1,1); 
plot(t_cont, x_cont, 'LineWidth',1.2, 'Color','#0072BD');
title('原始连续信号 x_a(t) = sin(20πt) + cos(40πt)（最高频率20Hz）');
xlabel('t (s)'); ylabel('幅值'); 
grid on; grid minor; % 显示细网格，更清晰

% 子图2：满足抽样定理的重构（fs=50Hz）
subplot(3,1,2); 
plot(t_cont, x_recon1, 'b-', 'LineWidth',1.2); hold on;
stem(t1, x1, 'r.', 'MarkerSize',10); % 抽样点用红色点标注
title('抽样频率fs=50Hz（满足奈奎斯特定理），重构信号');
xlabel('t (s)'); ylabel('幅值');
legend('重构信号','抽样点','Location','best'); 
grid on; grid minor;

% 子图3：不满足抽样定理的重构（fs=30Hz，混叠）
subplot(3,1,3); 
plot(t_cont, x_recon2, 'b-', 'LineWidth',1.2); hold on;
stem(t2, x2, 'r.', 'MarkerSize',10);
title('抽样频率fs=30Hz（不满足奈奎斯特定理），混叠失真');
xlabel('t (s)'); ylabel('幅值');
legend('重构信号','抽样点','Location','best'); 
grid on; grid minor;

% 调整窗口大小，避免内容重叠
set(gcf, 'Position', [100, 100, 900, 700]);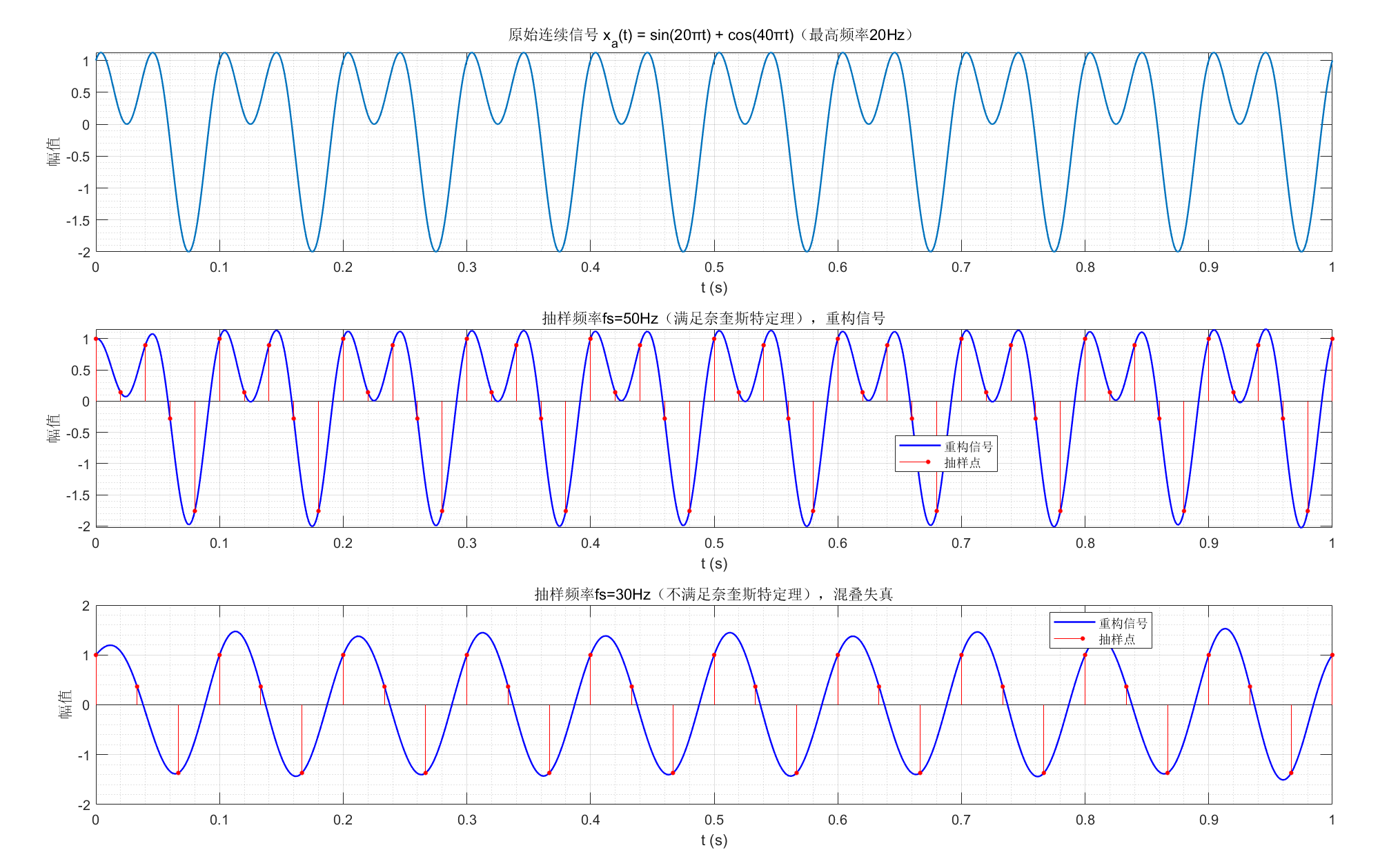

运行效果：

  • 满足抽样定理（fs=50Hz）：重构信号与原始连续信号几乎一致；
  • 不满足抽样定理（fs=30Hz）：重构信号出现严重混叠，完全偏离原始信号，直观理解抽样定理的重要性。

1.5 本章部分内容涉及的 MATLAB 函数及例题

核心函数总结

函数名 功能 示例
stem 绘制离散序列图 stem(n, x, 'filled')
conv 计算序列卷积和 conv(x, h)
xcorr 计算序列相关性 xcorr(x, y)
filter 求解差分方程 filter(b, a, x)
sinc 插值重构核心函数 sinc(fs*(t-t1))

综合例题（序列处理 + LTI 系统响应）

Matlab 复制代码 
% 1.5 综合例题：序列处理+LTI系统响应（去噪）- 清理隐形字符+优化
clc; clear; close all;

% ========== 需求：带噪声正弦序列通过LTI低通系统去噪 ==========
% 设置随机种子（固定噪声，保证每次运行结果一致）
rng(123); 

% 1. 生成输入序列
n = 0:50;                              % 自变量范围
x_clean = sin(0.1*pi*n);               % 干净的低频正弦序列（频率0.05π）
x_noise = x_clean + 0.2*randn(1, length(n)); % 叠加高斯白噪声

% 2. 定义LTI系统（10阶低通FIR滤波器，截止频率0.2π）
% fir1：FIR滤波器设计函数，10阶，截止频率0.2π（归一化频率，0~1对应0~π）
h = fir1(10, 0.2); 

% 3. 计算LTI系统输出（卷积，'same'保持输出长度与输入一致）
y = conv(x_noise, h, 'same'); 

% ========== 可视化对比（干净序列→噪声序列→去噪输出） ==========
figure('Color','w'); % 背景设为白色

% 子图1：干净输入序列
subplot(3,1,1); 
stem(n, x_clean, 'filled', 'Color','#0072BD'); % 蓝色填充
title('干净输入序列 x_clean(n) = sin(0.1πn)');
xlabel('n'); ylabel('幅值'); 
grid on; grid minor; % 细网格，更清晰

% 子图2：加噪声输入序列
subplot(3,1,2); 
stem(n, x_noise, 'filled', 'Color','#D95319'); % 橙色填充
title('加噪声输入序列 x_noise(n) = x_clean + 高斯白噪声');
xlabel('n'); ylabel('幅值'); 
grid on; grid minor;

% 子图3：LTI系统去噪输出
subplot(3,1,3); 
stem(n, y, 'filled', 'Color','#77AC30'); % 绿色填充
title('LTI低通系统输出 y(n)（去噪后）');
xlabel('n'); ylabel('幅值'); 
grid on; grid minor;

% 调整窗口大小，避免内容重叠
set(gcf, 'Position', [100, 100, 900, 700]);

% ========== 补充说明（可选） ==========
fprintf('LTI系统（低通滤波器）参数：10阶FIR，截止频率0.2π\n');
fprintf('去噪效果：噪声被抑制，输出接近干净正弦序列\n');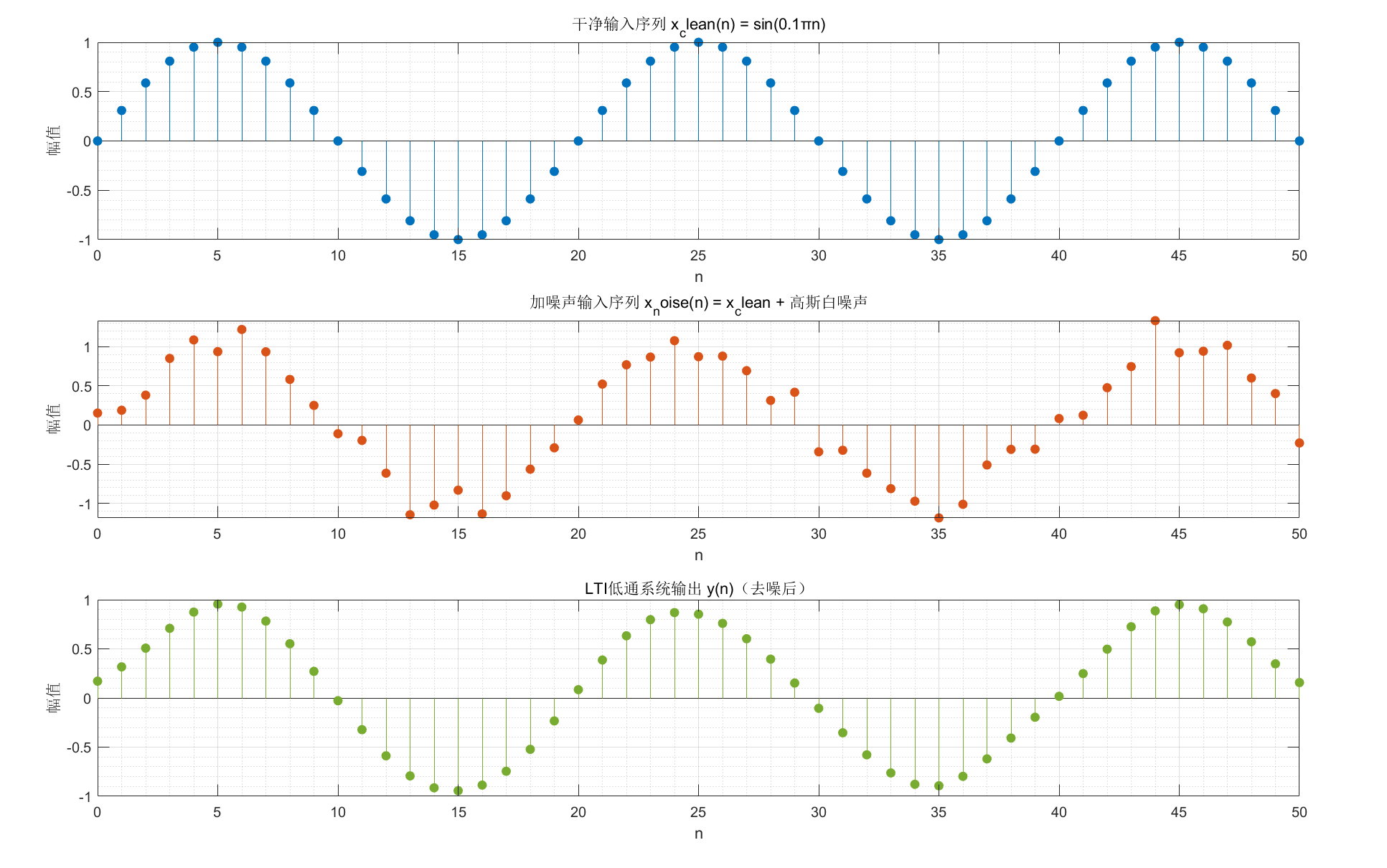

运行效果：清晰看到噪声序列经过 LTI 低通系统后，噪声被抑制，输出接近干净的正弦序列，体现数信处理的实际应用价值。

习题

  1. 编程实现序列的累加、差分运算，对比原始序列与运算结果；
  2. 验证不同频率正弦序列的周期性，总结周期计算规律；
  3. 设计一个因果稳定的 LTI 系统，计算其对矩形序列的响应；
  4. 改变抽样频率，观察不同程度的混叠现象，验证抽样定理；
  5. 用差分方程实现一个简单的数字滤波器，分析其对噪声信号的处理效果。

总结

  1. 离散时间信号（序列）是数信处理的基础，核心运算（移位、卷积、相关）可通过 MATLAB 可视化直观理解，卷积和是 LTI 系统分析的核心工具；
  2. LTI 系统需满足线性 + 移不变，因果系统 n<0 时单位抽样响应为 0，稳定系统单位抽样响应绝对和有限；
  3. 抽样定理是连续信号离散化的核心，抽样频率需大于 2 倍最高频率，否则会出现混叠，可通过 sinc 插值重构连续信号。
相关推荐
FMRbpm2 小时前
邻接矩阵练习1--------LCP 07.传递信息
数据结构·c++·算法·leetcode·深度优先·新手入门
ʚB҉L҉A҉C҉K҉.҉基҉德҉^҉大2 小时前
C++安全编程指南
开发语言·c++·算法
沛沛老爹2 小时前
Web开发者实战:多模态Agent技能开发——语音交互与合成技能集成指南
java·开发语言·前端·人工智能·交互·skills
zch不会敲代码2 小时前
深度学习之图像分类实战（食物分类）
人工智能·深度学习·分类
啊阿狸不会拉杆2 小时前
《数字信号处理》第 2 章 - z 变换与离散时间傅里叶变换（DTFT）
人工智能·算法·机器学习·信号处理·数字信号处理·dsp
hjs_deeplearning2 小时前
认知篇#15：ms-swift微调中gradient_accumulation_steps和warmup_ratio等参数的意义与设置
开发语言·人工智能·机器学习·swift·vlm
民乐团扒谱机2 小时前
【数模美赛=美术大赛？】O奖论文图片复刻——高级绘图matlab代码集锦，让你摆脱画图“一眼MATLAB”的痛苦！
前端·人工智能·matlab
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #146：LRU 缓存（双向链表、线程安全等多种实现方案详细解析）
算法·leetcode·lru·lru缓存·双向链表
武汉唯众智创2 小时前
全链路·工业级·强联动！物联网智慧城市实训平台，重塑职教实训新生态
人工智能·物联网·智慧城市·物联网实训平台·物联网智慧城市实训平台·智慧城市实训平台
热门推荐
01GitHub 镜像站点02【网络安全测试】Burp Suite工具使用说明、配置及常见问题（有关必回）03OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)04Claude Code Skills 实用使用手册05UV安装并设置国内源06struts2 XML外部实体注入漏洞复现（CVE-2025-68493）07Open Code教程（四）| 高级配置与集成08在VSCode配置Java开发环境的保姆级教程（适配各类AI编程IDE）09Linux下V2Ray安装配置指南10AI 规范驱动开发“三剑客”深度对比：Spec-Kit、Kiro 与 OpenSpec 实战指南