4.3 散射矩阵
前面讨论了为非TEM线定义电压和电流的困难程度。此外,测量微波频率下的电压和电流也很困难,因为直接测量通常会涉及给定方向的行波或驻波的幅值(得出功率)与相位。在与高频网络打交道时,这样的等效电压和电流及相关的阻抗和导纳在概念上会变得有些抽象。由散射矩阵给出的入射波、反射波和透射波的概念是与直接测量更为相符的表示方法。
类似于N端口网络的阻抗和导纳矩阵,散射矩阵提供从端口看去的完整网络描述。阻抗和导纳矩阵把端口上的电压和电流联系起来,而散射矩阵则把入射到端口的电压波与来自端口的反射波联系起来。对于某些元件和网络,可以用网络分析技术计算出散射矩阵。另外,可以直接用向量网络分析仪测量散射参量;图4.7是一台现代网络分析仪的照片。知道网络的散射参量后,

图4.7 Agilent N5247A可编程网络分析仪的实物照片。它测量射频和微波网络的散射参量,频率从10MHz到67GHz。这台网络分析仪是可编程的,可执行误差校正,并提供广泛的显示格式和数据转换。承蒙Agilent Technologies提供照片。
考虑图4.5中的N端口网络,其中 V n + V_{n}^{+} Vn+是入射到端口n的电压波振幅, V n − V_{n}^{-} Vn−是从端口n反射的电压波振幅。散射矩阵或S矩阵由这些入射和反射电压波之间的联系确定:
V 1 − V 2 − ⋮ V N − \] = \[ S 11 S 12 ⋯ S 1 N S 21 S 22 ⋯ S 2 N ⋮ ⋮ ⋱ ⋮ S N 1 S N 2 ⋯ S N N \] \[ V 1 + V 2 + ⋮ V N + \] \\begin{bmatrix}V_{1}\^{-}\\\\V_{2}\^{-}\\\\\\vdots\\\\V_{N}\^{-}\\end{bmatrix}=\\begin{bmatrix}S_{11}\&S_{12}\&\\cdots\&S_{1N}\\\\S_{21}\&S_{22}\&\\cdots\&S_{2N}\\\\\\vdots\&\\vdots\&\\ddots\&\\vdots\\\\S_{N1}\&S_{N2}\&\\cdots\&S_{NN}\\end{bmatrix}\\begin{bmatrix}V_{1}\^{+}\\\\V_{2}\^{+}\\\\\\vdots\\\\V_{N}\^{+}\\end{bmatrix} V1−V2−⋮VN− = S11S21⋮SN1S12S22⋮SN2⋯⋯⋱⋯S1NS2N⋮SNN V1+V2+⋮VN+ 或 V − = S V + ( 4.40 ) V\^{-}=S V\^{+} \\quad (4.40) V−=SV+(4.40) S矩阵的元素为 S i j = V i − V j + ∣ V k + = 0 , k ≠ j ( 4.41 ) S_{i j}=\\left.\\frac{V_{i}\^{-}}{V_{j}\^{+}}\\right\|_{V_{k}\^{+}=0,\\quad k \\neq j} \\quad (4.41) Sij=Vj+Vi− Vk+=0,k=j(4.41) 换言之,式(4.41)说,使用入射波电压 V j + V_{j}\^{+} Vj+激励j端口并测量从i端口出来的反射波电压 V j − V_{j}\^{-} Vj−,可得出 S i j S_{ij} Sij。同时**要求将除j端口外的所有其他端口上的入射波设为零,这意味着所有端口应端接匹配负载以避免出现反射。!!!(重要)** **要求将除j端口外的所有其他端口上的入射波设为零,这意味着所有端口应端接匹配负载以避免出现反射。!!!(重要)** **要求将除j端口外的所有其他端口上的入射波设为零,这意味着所有端口应端接匹配负载以避免出现反射。!!!(重要)** 这样, S i i S_{ii} Sii就是所有端口接匹配负载时向i端口看去的**反射系数** ,而 S i j S_{ij} Sij是所有其他端口接匹配负载时从j端口到i端口的**传输系数**。 #### **例题4.4 散射参量计算** 求图4.8给出的3dB衰减器电路的S参量。 **解** :由式(4.41)可知,当端口2接匹配负载( Z 0 = 50 Ω Z_{0}=50\\Omega Z0=50Ω)时,从端口1看去的反射系数 S 11 S_{11} S11为 S 11 = V 1 − V 1 + ∣ V 2 + = 0 = Γ ( 1 ) ∣ V 2 + = 0 = Z in ( 1 ) − Z 0 Z in ( 1 ) + Z 0 ∣ Z 0 在端口2 S_{11}=\\left.\\frac{V_{1}\^{-}}{V_{1}\^{+}}\\right\|_{V_{2}\^{+}=0}=\\left.\\Gamma\^{(1)}\\right\|_{V_{2}\^{+}=0}=\\left.\\frac{Z_{\\text{in}}\^{(1)}-Z_{0}}{Z_{\\text{in}}\^{(1)}+Z_{0}}\\right\|_{Z_{0}\\text{在端口2}} S11=V1+V1− V2+=0=Γ(1) V2+=0=Zin(1)+Z0Zin(1)−Z0 Z0在端口2 但是, Z in ( 1 ) = 8.56 + \[ 141.8 ( 8.56 + 50 ) \] / ( 141.8 + 8.56 + 50 ) = 50 Ω Z_{\\text{in}}\^{(1)}=8.56+\[141.8(8.56+50)\]/(141.8+8.56+50)=50\\Omega Zin(1)=8.56+\[141.8(8.56+50)\]/(141.8+8.56+50)=50Ω,所以有 S 11 = 0 S_{11}=0 S11=0。按电路的对称性有 S 22 = 0 S_{22}=0 S22=0。 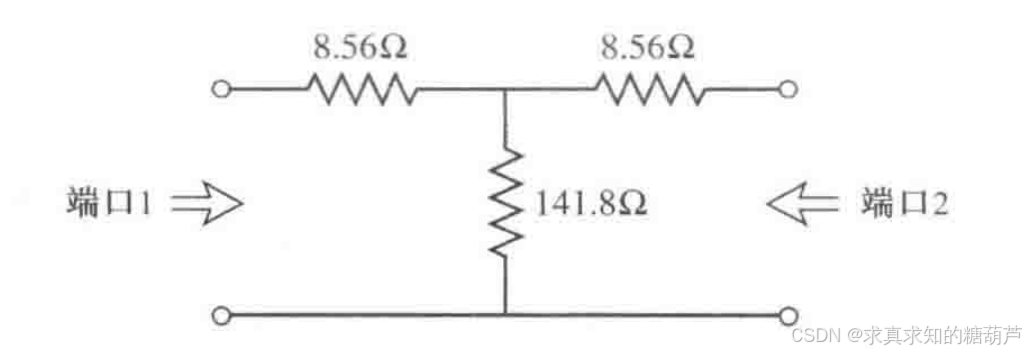 图4.8 具有50欧特征阻抗的3dB匹配衰减器(例题4.4) 在端口1上施加入射波 V 1 + V_{1}\^{+} V1+,并在端口2上测量出射波 V 2 − V_{2}\^{-} V2−,就可求出 S 21 S_{21} S21。这等效于从端口1到端口2的传输系数: S 21 = V 2 − V 1 + ∣ V 2 + = 0 S_{21}=\\left.\\frac{V_{2}\^{-}}{V_{1}\^{+}}\\right\|_{V_{2}\^{+}=0} S21=V1+V2− V2+=0 根据 S 11 = S 22 = 0 S_{11}=S_{22}=0 S11=S22=0可知,当端口2端接 Z 0 = 50 Ω Z_{0}=50\\Omega Z0=50Ω时 V 1 − = 0 V_{1}\^{-}=0 V1−=0,并且 V 2 + = 0 V_{2}\^{+}=0 V2+=0,在这情况下有 V 1 + = V 1 V_{1}\^{+}=V_{1} V1+=V1和 V 2 − = V 2 V_{2}\^{-}=V_{2} V2−=V2**( V 1 , V 2 V_{1},V_{2} V1,V2为端口1和端口2的总电压)**。所以在端口1上施加电压 V 1 V_{1} V1并使用二次分压,就可求出 V 2 − 或者 V 2 V_{2}\^{-}或者V_{2} V2−或者V2,它是端口2上跨接在 50 Ω 50\\Omega 50Ω负载电阻上的电压: V 2 − = V 2 = V 1 ( 41.44 41.44 + 8.56 ) ( 50 50 + 8.56 ) = 0.707 V 1 V_{2}\^{-}=V_{2}=V_{1}\\left(\\frac{41.44}{41.44+8.56}\\right)\\left(\\frac{50}{50+8.56}\\right)=0.707V_{1} V2−=V2=V1(41.44+8.5641.44)(50+8.5650)=0.707V1 式中, 41.44 = 141.8 × 58.56 / ( 141.8 + 58.56 ) 41.44=141.8\\times58.56/(141.8+58.56) 41.44=141.8×58.56/(141.8+58.56)是负载 50 Ω + 8.56 Ω 50\\Omega+8.56\\Omega 50Ω+8.56Ω与 141.8 Ω 141.8\\Omega 141.8Ω的并联电阻。这样,就有 S 12 = S 21 = 0.707 S_{12}=S_{21}=0.707 S12=S21=0.707。 输入功率为 ∣ V 1 + ∣ 2 / 2 Z 0 \|V_{1}\^{+}\|\^{2}/2Z_{0} ∣V1+∣2/2Z0时,输出功率为 ∣ V 2 − ∣ 2 / 2 Z 0 = ∣ S 21 V 1 + ∣ 2 / 2 Z 0 = ∣ S 21 ∣ 2 / 2 Z 0 ∣ V 1 + ∣ 2 = ∣ V 1 + ∣ 2 / 4 Z 0 \|V_{2}\^{-}\|\^{2}/2Z_{0}=\|S_{21}V_{1}\^{+}\|\^{2}/2Z_{0}=\|S_{21}\|\^{2}/2Z_{0}\|V_{1}\^{+}\|\^{2}=\|V_{1}\^{+}\|\^{2}/4Z_{0} ∣V2−∣2/2Z0=∣S21V1+∣2/2Z0=∣S21∣2/2Z0∣V1+∣2=∣V1+∣2/4Z0,它是输入功率的一半(-3dB)。 下面说明如何由Z(或Y)矩阵来确定S矩阵。首先,**必须假定所有端口的特征阻抗 Z 0 n Z_{0n} Z0n是相等的(讨论到广义散射矩阵时会去除这一假定)**。为方便起见,可设 Z 0 n = 1 Z_{0n}=1 Z0n=1。由式(4.24)可知, z = 0 z=0 z=0处端口n的总电压和电流为 V n = V n + + V n − ( 4.42 a ) V_{n}=V_{n}\^{+}+V_{n}\^{-} \\quad (4.42a) Vn=Vn++Vn−(4.42a) I n = I n + − I n − = V n + − V n − ( 4.42 b ) I_{n}=I_{n}\^{+}-I_{n}\^{-}=V_{n}\^{+}-V_{n}\^{-} \\quad (4.42b) In=In+−In−=Vn+−Vn−(4.42b) 利用式 V = Z I ( 4.25 ) V=ZI(4.25) V=ZI(4.25)中的Z和式(4.42),得到 Z I = Z V + − Z V − = V = V + + V − ZI=ZV\^{+}-ZV\^{-}=V=V\^{+}+V\^{-} ZI=ZV+−ZV−=V=V++V− 合并同类项 Z V + − V + = Z V − + V − ZV\^{+}-V\^{+}=ZV\^{-}+V\^{-} ZV+−V+=ZV−+V− ( Z + E ) V − = ( Z − E ) V + ( 4.43 ) (Z+E)V\^{-}=(Z-E)V\^{+} \\quad (4.43) (Z+E)V−=(Z−E)V+(4.43) **式中,E是单位矩阵,它定义为** E = \[ 1 0 ⋯ 0 0 1 ⋯ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ 1 \] \\boldsymbol{E}=\\begin{bmatrix}1\&0\&\\cdots\&0\\\\0\&1\&\\cdots\&0\\\\\\vdots\&\\vdots\&\\ddots\&\\vdots\\\\0\&0\&\\cdots\&1\\end{bmatrix} E= 10⋮001⋮0⋯⋯⋱⋯00⋮1 比较式(4.43)与式(4.40)得 S = ( Z + E ) − 1 ( Z − E ) ( 4.44 ) S=(Z+E)\^{-1}(Z-E) \\quad (4.44) S=(Z+E)−1(Z−E)(4.44) 它给出了用阻抗矩阵表示的散射矩阵。注意,对于一端口网络(矩阵退化) S 11 = z 11 − 1 z 11 + 1 = Γ S_{11}=\\frac{z_{11}-1}{z_{11}+1}=\\Gamma S11=z11+1z11−1=Γ 该结果与向负载看去的反射系数(其归一化输入阻抗为 z 11 z_{11} z11其中 Z 0 n = 1 Z_{0n}=1 Z0n=1)一致。 为了求出用S表示的Z,可把式(4.44)改写为 Z S + E S = Z − E ZS+ES=Z-E ZS+ES=Z−E,并解出Z: Z = ( E + S ) ( E − S ) − 1 ( 4.45 ) Z=(E+S)(E-S)\^{-1} \\quad (4.45) Z=(E+S)(E−S)−1(4.45) #### 4.3.1 互易网络与无耗网络 如4.2节中讨论的那样,对于互易网络,阻抗和导纳矩阵是对称的;对于无耗网络,它们是纯虚数。对于这种类型的网络,散射矩阵有其特殊性质。下面说明**互易网络的S矩阵是对称的,而无耗网络的S矩阵是幺正矩阵**。 式(4.42a)和式(4.42b)相加得 V n + = 1 2 ( V n + I n ) V_{n}\^{+}=\\frac{1}{2}\\left(V_{n}+I_{n}\\right) Vn+=21(Vn+In) 或 V + = 1 2 ( Z + E ) I ( 4.46 a ) V\^{+}=\\frac{1}{2}(Z+E)I \\quad (4.46a) V+=21(Z+E)I(4.46a) 式(4.42a)和式(4.42b)相减得 V n − = 1 2 ( V n − I n ) V_{n}\^{-}=\\frac{1}{2}\\left(V_{n}-I_{n}\\right) Vn−=21(Vn−In) 或 V − = 1 2 ( Z − E ) I ( 4.46 b ) V\^{-}=\\frac{1}{2}(Z-E)I \\quad (4.46b) V−=21(Z−E)I(4.46b) 式(4.46a)和式(4.46b)相除可消去I,得到 V − = ( Z − E ) ( Z + E ) − 1 V + V\^{-}=(Z-E)(Z+E)\^{-1} V\^{+} V−=(Z−E)(Z+E)−1V+ 所以有 S = ( Z − E ) ( Z + E ) − 1 ( 4.47 ) S=(Z-E)(Z+E)\^{-1} \\quad (4.47) S=(Z−E)(Z+E)−1(4.47) 取式(4.47)的**转置**(交换顺序分别转置) S T = { ( Z + E ) − 1 } T ( Z − E ) T S\^{T}=\\left\\{(Z+E)\^{-1}\\right\\}\^{T}(Z-E)\^{T} ST={(Z+E)−1}T(Z−E)T 由于单位矩阵E是对角矩阵,所以 E T = E E\^{T}=E ET=E;若网络是互易的,则Z是对称的,因此有 Z T = Z Z\^{T}=Z ZT=Z。于是上式简化为 S T = ( Z + E ) − 1 ( Z − E ) S\^{T}=(Z+E)\^{-1}(Z-E) ST=(Z+E)−1(Z−E) 它等同于式(4.44)。这就证明了互易网络有 S = S T ( 4.48 ) S=S\^{T} \\quad (4.48) S=ST(4.48) 若网络是无耗的,则无实功率传送给网络。这样,**若所有端口的特征阻抗都相同并设为1**,则传送到网络的平均功率为 P avg = 1 2 Re { V t I ∗ } = 1 2 Re { ( V + t + V − t ) ( V + ∗ − V − ∗ ) } = 1 2 Re { V + t V + ∗ − V + t V − ∗ + V − t V + ∗ − V − t V − ∗ } ( 4.49 ) = 1 2 V + t V + ∗ − 1 2 V − t V − ∗ = 0 \\begin{aligned} P_{\\text {avg }}\&=\\frac{1}{2} \\operatorname{Re}\\left\\{V\^{t} I\^{\*}\\right\\}=\\frac{1}{2} \\operatorname{Re}\\left\\{\\left(V\^{+t}+V\^{-t}\\right)\\left(V\^{+\^{\*}}-V\^{-\^{\*}}\\right)\\right\\} \\\\ \&=\\frac{1}{2} \\operatorname{Re}\\left\\{V\^{+t} V\^{+\^{\*}}-V\^{+t} V\^{-\^{\*}}+V\^{-t} V\^{+\^{\*}}-V\^{-t} V\^{-\^{\*}}\\right\\} \\quad (4.49)\\\\ \&=\\frac{1}{2} V\^{+t} V\^{+\^{\*}}-\\frac{1}{2} V\^{-t} V\^{-\^{\*}}=0 \\end{aligned} Pavg =21Re{VtI∗}=21Re{(V+t+V−t)(V+∗−V−∗)}=21Re{V+tV+∗−V+tV−∗+V−tV+∗−V−tV−∗}(4.49)=21V+tV+∗−21V−tV−∗=0 因为项**− V + t V − ∗ + V − t V + ∗ -V\^{+t} V\^{-\^{\*}}+V\^{-t} V\^{+\^{\*}} −V+tV−∗+V−tV+∗这两项均为标量,是行向量和列向量内积,具有 A − ( A ∗ ) T A-(A\^{\*})\^T A−(A∗)T的形式,实部抵消**,在式(4.49)的其余项中, ( 1 / 2 ) V + t V + ∗ (1/2)V\^{+t} V\^{+\^{\*}} (1/2)V+tV+∗表示总入射功率,(1/2) V − t V − ∗ V\^{-t}V\^{-\^{\*}} V−tV−∗表示总反射功率。所以对于无耗结,直观的结论是入射功率等于反射功率: V + t V + ∗ = V − t V − ∗ ( 4.50 ) V\^{+t}V\^{+\^{\*}}=V\^{-t}V\^{-\^{\*}} \\quad (4.50) V+tV+∗=V−tV−∗(4.50) 把 V − = S V + V\^{-}=SV\^{+} V−=SV+代入式(4.50)得,**注意转置运算交换顺序** V + t V + ∗ = V + t S t S ∗ V + ∗ V\^{+t}V\^{+\^{\*}}=V\^{+t}S\^{t}S\^{\*}V\^{+\^{\*}} V+tV+∗=V+tStS∗V+∗ 因此对于非零的 V + V\^{+} V+有 S T S ∗ = E S\^{T}S\^{\*}=E STS∗=E 或 S ∗ = { S T } − 1 ( 4.51 ) S\^{\*}=\\left\\{S\^{T}\\right\\}\^{-1} \\quad (4.51) S∗={ST}−1(4.51) 满足式(4.51)给出的条件的矩阵**(共轭乘以转置等于单位阵),称为幺正矩阵**。 矩阵方程(4.51)可写成累加形式: ∑ k = 1 N S k i S k j ∗ = S i j , 对所有 i , j ( 4.52 ) \\sum_{k=1}\^{N} S_{ki} S_{kj}\^{\*}=S_{ij}, \\quad \\text {对所有} i, j \\quad (4.52) k=1∑NSkiSkj∗=Sij,对所有i,j(4.52) 式中,若 i = j i=j i=j,则 δ i j = 1 \\delta_{ij}=1 δij=1;若 i ≠ j i\\neq j i=j,则 δ i j = 0 \\delta_{ij}=0 δij=0, δ i j \\delta_{ij} δij是Kronecker δ \\delta δ符号。这样, i = j i=j i=j,式(4.52)化为 ∑ k = 1 N S k i S k j ∗ = 1 ( 4.53 a ) \\sum_{k=1}\^{N} S_{ki} S_{kj}\^{\*}=1 \\quad (4.53a) k=1∑NSkiSkj∗=1(4.53a) i ≠ j i\\neq j i=j时,式(4.52)化为 ∑ k = 1 N S k i S k j ∗ = 0 , i ≠ j ( 4.53 b ) \\sum_{k=1}\^{N} S_{ki} S_{kj}\^{\*}=0, \\quad i\\neq j \\quad (4.53b) k=1∑NSkiSkj∗=0,i=j(4.53b) 换言之,式(4.53a)说明S的任意一列与该列的共轭的点乘为1;式(4.53b)说明S的任意一列与不同列的共轭的点乘为零(正交)。由式(4.51)得 S S ∗ T = E S S\^{\*T}=E SS∗T=E 因此,对散射矩阵的各行可做出同样的陈述。 #### **例题4.5 散射参量的应用** 已知二端口网络有如下散射矩阵: S = \[ 0.15 ∠ 0 ∘ 0.85 ∠ − 45 ∘ 0.85 ∠ 45 ∘ 0.2 ∠ 0 ∘ \] S=\\left\[\\begin{array}{cc}0.15\\angle 0\^{\\circ}\&0.85\\angle-45\^{\\circ}\\\\0.85\\angle 45\^{\\circ}\&0.2\\angle 0\^{\\circ}\\end{array}\\right\] S=\[0.15∠0∘0.85∠45∘0.85∠−45∘0.2∠0∘
判定网络是互易的还是无耗的。若端口2接有匹配负载,则从端口1看去的回波损耗是多少?若端口2短路,则从端口1看去的回波损耗又是多少?
解 :由于S是非对称的,所以网络是非互易的。假如网络是无耗的,则S参量应满足式(4.53)。取其第1列[即在式(4.53a)中 i = 1 i=1 i=1]有
∣ S 11 ∣ 2 + ∣ S 21 ∣ 2 = ( 0.15 ) 2 + ( 0.85 ) 2 = 0.745 ≠ 1 \left|S_{11}\right|^{2}+\left|S_{21}\right|^{2}=(0.15)^{2}+(0.85)^{2}=0.745\neq 1 ∣S11∣2+∣S21∣2=(0.15)2+(0.85)2=0.745=1
因此网络不是无耗的。
当端口2接有匹配负载时,从端口1看去的反射系数是 Γ = S 11 = 0.15 \Gamma=S_{11}=0.15 Γ=S11=0.15。所以回波损耗是
R L = − 20 lg ∣ Γ ∣ = − 20 lg ( 0.15 ) = 16.5 d B \mathrm{RL}=-20\lg |\Gamma|=-20\lg (0.15)=16.5\mathrm{~dB} RL=−20lg∣Γ∣=−20lg(0.15)=16.5 dB
当端口2被短路时,向端口1看去的反射系数可按如下方式求出。从散射矩阵的定义和此时 V 2 + = − V 2 − V_{2}^{+}=-V_{2}^{-} V2+=−V2−的事实(在端口2短路)出发,可写出
V 1 − = S 11 V 1 + + S 12 V 2 + = S 11 V 1 + − S 12 V 2 − V_{1}^{-}=S_{11} V_{1}^{+}+S_{12} V_{2}^{+}=S_{11} V_{1}^{+}-S_{12} V_{2}^{-} V1−=S11V1++S12V2+=S11V1+−S12V2−
第二个方程给出
用 V 1 + V_{1}^{+} V1+除第一个方程,并利用上式的结果,就可给出向端口1看去的反射系数为
Γ = V 1 − V 1 + = S 11 − S 12 V 2 − V 1 + = S 11 − S 12 S 21 1 + S 22 = 0.15 − ( 0.85 ∠ − 45 ∘ ) × ( 0.85 ∠ 45 ∘ ) 1 + 0.2 = − 0.452 \begin{aligned} \Gamma=\frac{V_{1}^{-}}{V_{1}^{+}} &= S_{11}-S_{12}\frac{V_{2}^{-}}{V_{1}^{+}}=S_{11}-\frac{S_{12} S_{21}}{1+S_{22}}\\ & =0.15-\frac{\left(0.85\angle-45^{\circ}\right)\times\left(0.85\angle 45^{\circ}\right)}{1+0.2}=-0.452 \end{aligned} Γ=V1+V1−=S11−S12V1+V2−=S11−1+S22S12S21=0.15−1+0.2(0.85∠−45∘)×(0.85∠45∘)=−0.452
所以回波损耗 R L = − 20 lg ∣ Γ ∣ = − 20 lg ( 0.452 ) = 6.9 d B \mathrm{RL}=-20\lg |\Gamma|=-20\lg (0.452)=6.9\mathrm{~dB} RL=−20lg∣Γ∣=−20lg(0.452)=6.9 dB。
理解S参量时有一点很重要:向端口n看去的反射系数并不等于 S n n S_{nn} Snn;只有当所有的其他端口都匹配时才会这样(这一点已在上面的例题中说明)。与此相仿,除非所有其他端口都匹配,否则从端口m到端口n的传输系数就不等于 S m n S_{mn} Smn。网络的S参量只是网络本身的特性(假定网络是线性的),它是在所有端口均匹配的条件下定义的 。改变网络的端接或激励条件不会改变网络的S参量,但会改变向给定端口看去的反射系数或两个端口之间的传输系数。