为什么要对图像进行锐化处理?
在对图像进行增强处理前,一般会进行平滑处理来减少/消除噪声。噪声的能量集中在高频部分,边缘信息的能量也是集中在高频部分,所以在进行平滑操作对噪声进行处理的时候,也会影响到边缘,使边缘变得模糊。此时就需要反处理图像,使边缘变得清晰,这种反处理就是图像的锐化算法。进行图像锐化的另外一个原因,是获得更清晰的边缘轮廓,方便计算机提取物体的边界,为后续操作做铺垫。
目录
一.图像的锐化原理
对图像的平滑处理一般是求积分,那么实现图像的锐化,就要进行反处理,进行微分操作。由于微分操作会放大噪声,如果先进行锐化处理后进行平滑处理将达不到一个好的图像处理效果,所以需要先进行平滑处理,后再对图像进行锐化处理。图像的锐化其实就是提取物体的边缘轮廓,将这个边缘轮廓加到原图上,就能获得一个更清晰的边缘轮廓显示效果。
物体的边缘分为:
1.阶跃状边缘:两边的像素灰度显著不同;
2.屋顶状边缘:它位于像素灰度值从增加到减少(或者相反)的转折点。
一般考虑每个像素在局部的变化(NxN窗口),利用边缘邻近一阶/二阶方向导数变化规律来检测图像的物体边缘。
一阶微分运算的边缘检测算子包括:Robert算子,Sobel算子以及Prewitt算子。
二阶微分算子有:Laplacian算子等。
一阶微分主要是指梯度模运算,图像f(x,y)在点(x,y)处的梯度定义为:
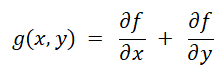
因为处理的图像数据是离散的,所以可以用差分来代替微分:
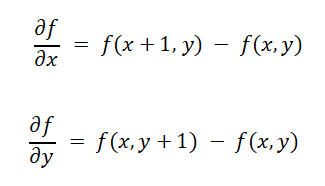
梯度的幅值即为模值:
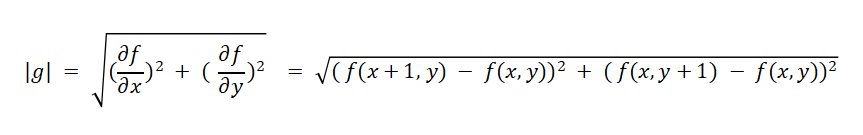
二阶微分具有各向同性,旋转不变性的特征,所以满足不同走向的图像边缘锐化的要求。
用差分代替微分,二阶微分可以表示为:
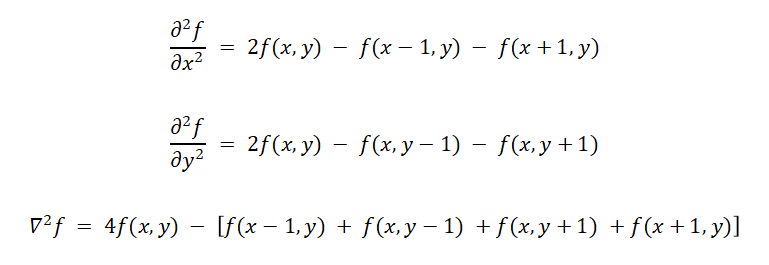
二.Robert锐化算法
Robert算子是一种利用局部(2X2窗口)差分寻找边缘的算子方法,即通过计算对角方向相邻的两个像素之差。Robert的水平及垂直方向的算子为:
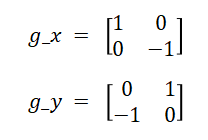
Robert的边缘检测算法流程如下:
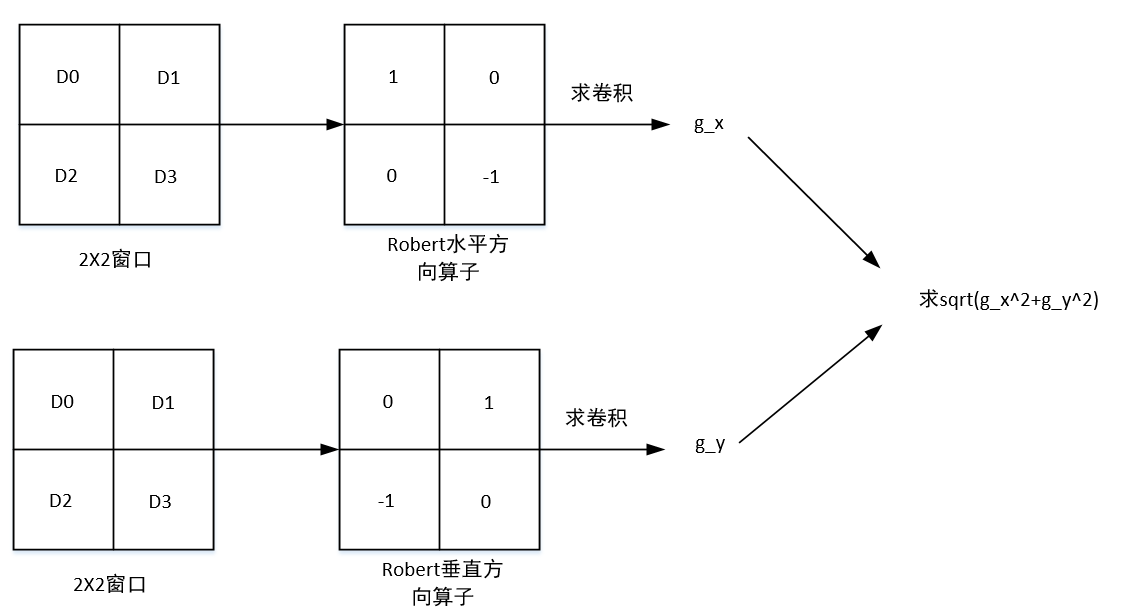
将得到的边缘数据加上原图数据就是实现Robert锐化算法。
MATLAB实现如下:
Matlab
clc;
clear all;
img = imread('D:\matlab file\image_edge_detector\yu.bmp');
img = rgb2gray(img);
figure('Position',[500,200,1000,500]);
subplot(1,3,1);imshow(img);title('原图');
[h,w] = size(img);
img1 = zeros(h,w);
g_x = [1,0,0,-1];
g_y = [0,1,-1,0];
img = double(img);
for i = 1:h
for j = 1:w
if(i>h-1 || j>w-1)
img1(i,j) = 0;
else
img_x = g_x(1)*img(i,j) + g_x(2)*img(i,j+1) + g_x(3)*img(i+1,j) + g_x(4)*img(i+1,j+1);
img_y = g_y(1)*img(i,j) + g_y(2)*img(i,j+1) + g_y(3)*img(i+1,j) + g_y(4)*img(i+1,j+1);
img1(i,j) = sqrt(img_x^2 +img_y^2);
end
end
end
img1 = uint8(img1);
subplot(1,3,2);imshow(img1);title('Robert边缘检测');
img2 = uint8(img) + img1;
subplot(1,3,3);imshow(img2);title('Robert锐化图像');结果显示如下:

与原图相比,经过Robert锐化算法后的原图具有更清晰的轮廓。
三.Sobel锐化算法
Robert只是单纯采用微分锐化图像,会使噪声得到增强。而Sobel先求平均后求微分,最后求梯度算子,可以很好地抑制噪声。但是Sobel对边缘的定位检测不如Robert敏感。
Sobel的水平垂直算子如下所示:
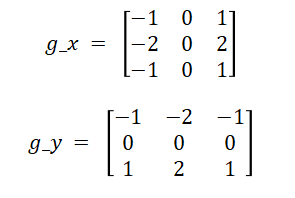
Sobel的边缘检测算法流程如下:
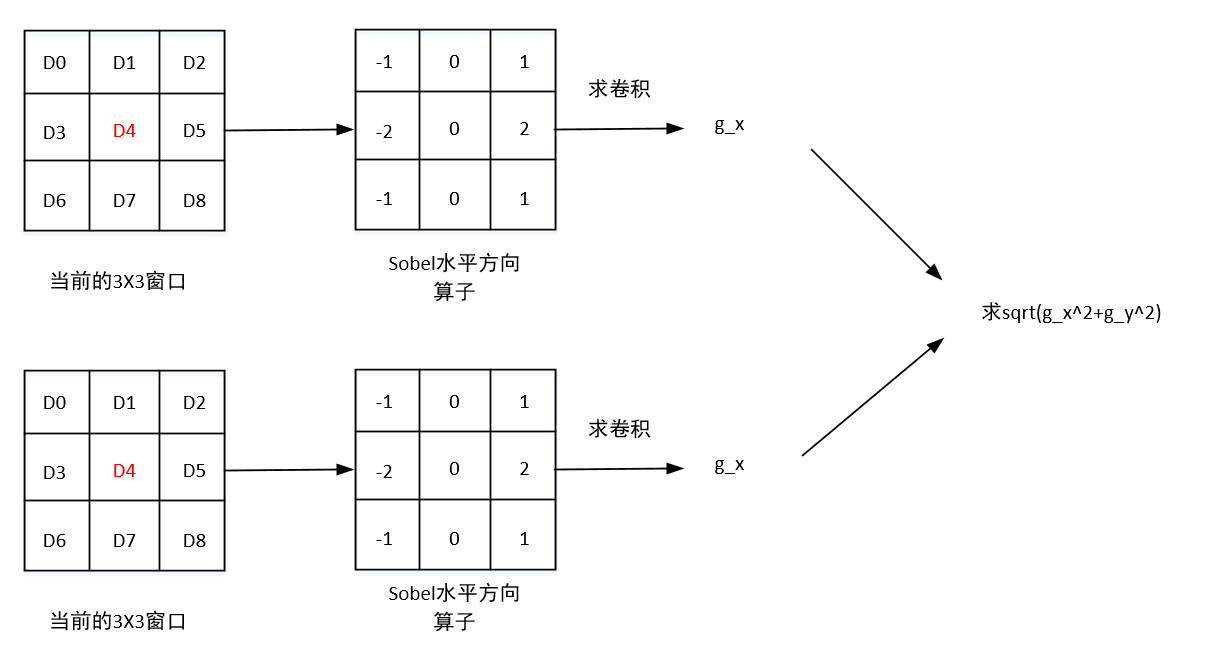
MATLAB实现代码如下:
Matlab
clc;
clear all;
img = imread('D:\matlab file\image_edge_detector\yu.bmp');
img = rgb2gray(img);
figure('Position',[500,200,1000,500]);
subplot(1,3,1);imshow(img);title('原图');
[h,w] = size(img);
img1 = zeros(h,w);
n = 3;
d = floor(n/3);
sobel_x = [-1 0 1 -2 0 2 -1 0 1]; %水平方向上的sobel算子
sobel_y = [-1 -2 -1 0 0 0 1 2 1]; %垂直方向上的sobel算子
img = double(img); %双精度浮点数
for i = 1:h
for j = 1:w
if(i<d+1 || i>h-d || j<d+1 || j>w-d)
img1(i,j) = 0; %边缘赋原值
else
g_x = sobel_x(1)*img(i-1,j-1)+sobel_x(2)*img(i-1,j)+sobel_x(3)*img(i-1,j+1)+sobel_x(4)*img(i,j-1)+sobel_x(5)*img(i,j)+sobel_x(6)*img(i,j+1)+sobel_x(7)*img(i+1,j-1)+sobel_x(8)*img(i+1,j)+sobel_x(9)*img(i+1,j+1);
g_y = sobel_y(1)*img(i-1,j-1)+sobel_y(2)*img(i-1,j)+sobel_y(3)*img(i-1,j+1)+sobel_y(4)*img(i,j-1)+sobel_y(5)*img(i,j)+sobel_y(6)*img(i,j+1)+sobel_y(7)*img(i+1,j-1)+sobel_y(8)*img(i+1,j)+sobel_y(9)*img(i+1,j+1);
img1(i,j) = sqrt(g_x^2 + g_y^2);
end
end
end
img1 = uint8(img1);
subplot(1,3,2);imshow(img1);title('Sobel边缘检测');
img2 = uint8(img) + img1;
subplot(1,3,3);imshow(img2);title('Sobel锐利图像');结果显示如下:
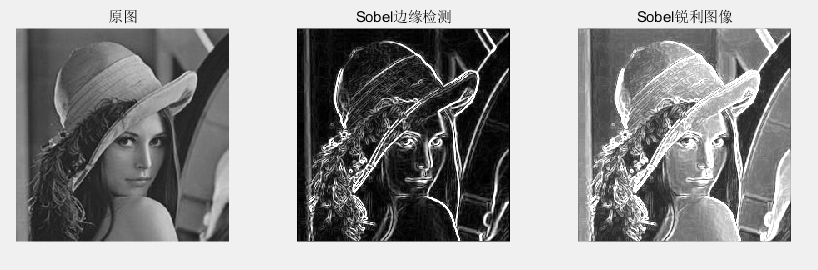
四.Laplacian锐化算法
Laplacian属于二阶微分的锐化算法。其算子为:
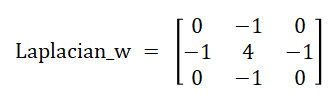
Laplacian的边缘检测算法流程如下:
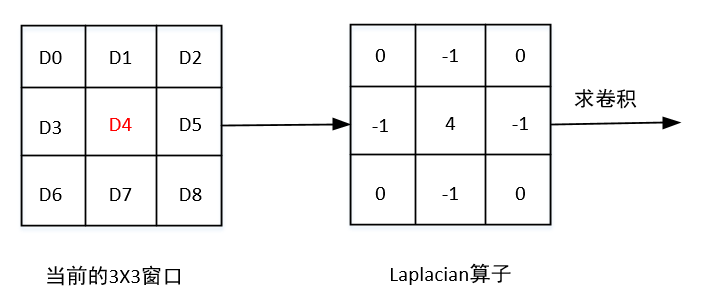
MATLAB实现代码如下:
Matlab
clc;
clear all;
img = imread('D:\matlab file\image_edge_detector\yu.bmp');
img = rgb2gray(img);
figure('Position',[500,200,1000,500]);
subplot(1,3,1);imshow(img);title('原图');
[h,w] = size(img);
img1 = zeros(h,w);
n = 3;
d = floor(n/3);
laplacian_w = [0,-1,0,-1,4,-1,0,-1,0];
img = double(img); %双精度浮点数
for i = 1:h
for j = 1:w
if(i<d+1 || i>h-d || j<d+1 || j>w-d)
img1(i,j) = 0; %边缘赋原值
else
img1(i,j) = laplacian_w(1)*img(i-1,j-1) + laplacian_w(2)*img(i-1,j) + laplacian_w(3)*img(i-1,j+1) + laplacian_w(4)*img(i,j-1) + laplacian_w(5)*img(i,j) + laplacian_w(6)*img(i,j+1) + laplacian_w(7)*img(i+1,j-1) + laplacian_w(8)*img(i+1,j) + laplacian_w(9)*img(i+1,j+1);
end
end
end
img1 = uint8(img1);
subplot(1,3,2);imshow(img1);title('Laplacian边缘检测');
img2 = uint8(img) + img1;
subplot(1,3,3);imshow(img2);title('Laplacian锐利图像');结果显示如下:

参考自《基于MATLAB与FPGA的图像处理教程》。
内容仅供学习使用,请勿转载。
如有问题,欢迎指正。