4.3.2 参考平面的移动
由于S参量关联了入射到网络和从网络反射的行波的振幅(幅值和相位),因此必须确定网络的每个端口的相位参考平面。下面说明当参考平面从原位置zn=0z_{n}=0zn=0移动时,S参量是如何转换的。
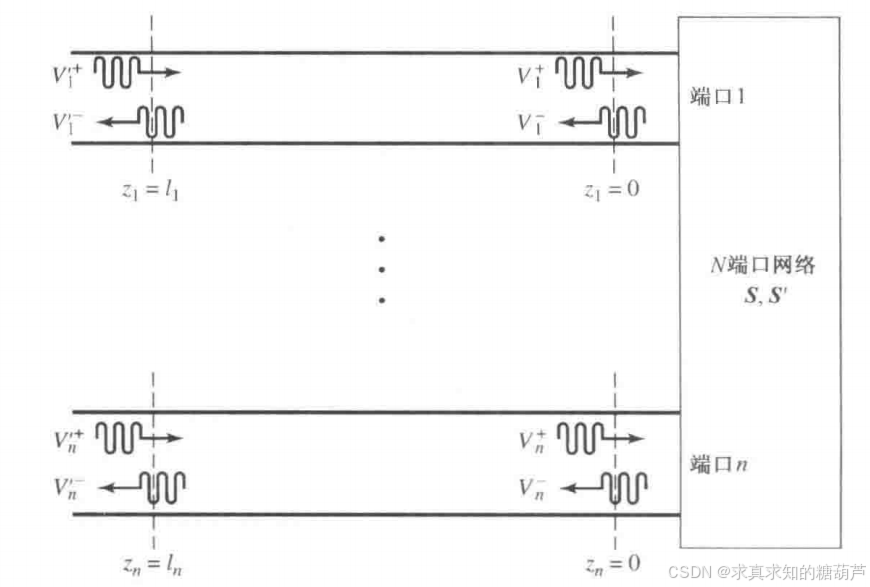
图4.9移动N端口网络的参考平面
现在考虑图4.9中的一个N端口网络,设第n个端口的原端平面位置为zn=0z_{n}=0zn=0,其中znz_{n}zn是沿馈送到第n个端口的传输线量度的任一坐标点。这个网络的散射矩阵连同这组端平面用S来表示。现在考虑第n个端口位于zn=ℓnz_{n}=\ell_{n}zn=ℓn的一组新的端平面,并将这个新散射矩阵表示为S′S^{\prime}S′。则用入射和反射端口电压表示时,有
V−=SV+(4.54a) V^{-}=S V^{+} \quad (4.54a) V−=SV+(4.54a)
V′=S′V′+(4.54b) V^{\prime}=S^{\prime} V^{\prime+} \quad (4.54b) V′=S′V′+(4.54b)
式中,不带撇号的量是以原来在zn=0z_{n}=0zn=0的端平面作为参考的,而带撇号的量是以在zn=ℓnz_{n}=\ell_{n}zn=ℓn处的新端平面作为参考的。
从无耗传输线上行波的理论出发,可把新波的振幅与原波的振幅通过下式联系起来:
Vn′+=Vn+ejθn(4.55a) V_{n}^{\prime+}=V_{n}^{+} e^{j\theta_{n}} \quad (4.55a) Vn′+=Vn+ejθn(4.55a)
Vn′−=Vn−e−jθn(4.55b) V_{n}^{\prime-}=V_{n}^{-} e^{-j\theta_{n}} \quad (4.55b) Vn′−=Vn−e−jθn(4.55b)
式中θn=βnℓn\theta_{n}=\beta_{n}\ell_{n}θn=βnℓn是第n个端口的参考平面向外移动的电长度,Vn+Vn−V_{n}^{+}V_{n}^{-}Vn+Vn−为两个列向量。
把式(4.55)用矩阵形式写出,并把它代入式(4.54a),得
ejθ10ejθ2⋱0ejθN\]V′−=S\[e−jθ10e−jθ2⋱0e−jθN\]V′+ \\left\[\\begin{array}{ccc} \\mathrm{e}\^{\\mathrm{j}\\theta_{1}} \& \&\&0 \\\\ \&\\mathrm{e}\^{\\mathrm{j}\\theta_{2}} \& \\\\ \&\&\\ddots \& \\\\ 0 \& \&\&\\mathrm{e}\^{\\mathrm{j}\\theta_{N}} \\end{array}\\right\] V\^{\\prime-}=S\\left\[\\begin{array}{ccc} \\mathrm{e}\^{-\\mathrm{j}\\theta_{1}} \& \&\&0 \\\\ \&\\mathrm{e}\^{-\\mathrm{j}\\theta_{2}} \& \\\\ \&\&\\ddots \& \\\\ 0 \&\&\& \\mathrm{e}\^{-\\mathrm{j}\\theta_{N}} \\end{array}\\right\] V\^{\\prime+} ejθ10ejθ2⋱0ejθN V′−=S e−jθ10e−jθ2⋱0e−jθN V′+ *** ** * ** *** #### 复习:正对角线矩阵的逆 设 AAA 是一个 n×nn \\times nn×n 的正对角线矩阵: A=\[a100⋯00a20⋯000a3⋯0⋮⋮⋮⋱⋮000⋯an\] A = \\begin{bmatrix} a_{1} \& 0 \& 0 \& \\cdots \& 0 \\\\ 0 \& a_{2} \& 0 \& \\cdots \& 0 \\\\ 0 \& 0 \& a_{3} \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& 0 \& \\cdots \& a_{n} \\end{bmatrix} A= a100⋮00a20⋮000a3⋮0⋯⋯⋯⋱⋯000⋮an 其逆矩阵为: A−1=\[1a100⋯001a20⋯0001a3⋯0⋮⋮⋮⋱⋮000⋯1an\](a) A\^{-1} = \\begin{bmatrix} \\frac{1}{a_{1}} \& 0 \& 0 \& \\cdots \& 0 \\\\ 0 \& \\frac{1}{a_{2}} \& 0 \& \\cdots \& 0 \\\\ 0 \& 0 \& \\frac{1}{a_{3}} \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& 0 \& \\cdots \& \\frac{1}{a_{n}} \\end{bmatrix}\\quad (a) A−1= a1100⋮00a210⋮000a31⋮0⋯⋯⋯⋱⋯000⋮an1 (a) 其中 ai≠0a_i \\neq 0ai=0 对所有的 i=1,2,...,ni = 1, 2, \\dots, ni=1,2,...,n。 ##### 证明 矩阵 AAA 的行列式为: det(A)=∏i=1nai \\operatorname{det}(A) = \\prod_{i=1}\^{n} a_i det(A)=i=1∏nai 对于矩阵 AAA 的对角线元素 aia_iai,其代数余子式 MiM_iMi 为: Mi=∏j=1j≠inaj∏j=1naj=1ai M_i = \\frac{\\prod\\limits_{\\substack{j=1 \\\\ j \\neq i}}\^{n} a_j}{\\prod\\limits_{j=1}\^{n} a_j} = \\frac{1}{a_i} Mi=j=1∏najj=1j=i∏naj=ai1 则伴随矩阵 A∗A\^\*A∗ 的对角线元素的值为: Aii∗=(−1)2i⋅Mi=Mi=1ai A_{ii}\^\* = (-1)\^{2i} \\cdot M_i = M_i = \\frac{1}{a_i} Aii∗=(−1)2i⋅Mi=Mi=ai1 由于矩阵 AAA 是对角矩阵,其伴随矩阵也是对角矩阵,且 A−1=1det(A)A∗A\^{-1} = \\frac{1}{\\operatorname{det}(A)} A\^\*A−1=det(A)1A∗。因此: A−1=1∏i=1nai⋅\[∏j=1j≠1naj0⋯00∏j=1j≠2naj⋯0⋮⋮⋱⋮00⋯∏j=1j≠nnaj\] A\^{-1} = \\frac{1}{\\prod_{i=1}\^n a_i} \\cdot \\begin{bmatrix} \\prod\\limits_{\\substack{j=1 \\\\ j \\neq 1}}\^{n} a_j \& 0 \& \\cdots \& 0 \\\\ 0 \& \\prod\\limits_{\\substack{j=1 \\\\ j \\neq 2}}\^{n} a_j \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& \\cdots \& \\prod\\limits_{\\substack{j=1 \\\\ j \\neq n}}\^{n} a_j \\end{bmatrix} A−1=∏i=1nai1⋅ j=1j=1∏naj0⋮00j=1j=2∏naj⋮0⋯⋯⋱⋯00⋮j=1j=n∏naj 化简后得到: A−1=\[1a10⋯001a2⋯0⋮⋮⋱⋮00⋯1an\] A\^{-1} = \\begin{bmatrix} \\frac{1}{a_1} \& 0 \& \\cdots \& 0 \\\\ 0 \& \\frac{1}{a_2} \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& \\cdots \& \\frac{1}{a_n} \\end{bmatrix} A−1= a110⋮00a21⋮0⋯⋯⋱⋯00⋮an1 证毕。 #### 复习:对角分块矩阵的逆 设 AAA 是一个 n×nn \\times nn×n 的对角分块矩阵: A=\[A100⋯00A20⋯000A3⋯0⋮⋮⋮⋱⋮000⋯Ak\] A = \\begin{bmatrix} A_1 \& 0 \& 0 \& \\cdots \& 0 \\\\ 0 \& A_2 \& 0 \& \\cdots \& 0 \\\\ 0 \& 0 \& A_3 \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& 0 \& \\cdots \& A_k \\end{bmatrix} A= A100⋮00A20⋮000A3⋮0⋯⋯⋯⋱⋯000⋮Ak 其中 A1,A2,...,AkA_1, A_2, \\dots, A_kA1,A2,...,Ak 均为可逆方阵,其逆矩阵为: A−1=\[A1−100⋯00A2−10⋯000A3−1⋯0⋮⋮⋮⋱⋮000⋯Ak−1\](b) A\^{-1} = \\begin{bmatrix} A_1\^{-1} \& 0 \& 0 \& \\cdots \& 0 \\\\ 0 \& A_2\^{-1} \& 0 \& \\cdots \& 0 \\\\ 0 \& 0 \& A_3\^{-1} \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& 0 \& \\cdots \& A_k\^{-1} \\end{bmatrix}\\quad (b) A−1= A1−100⋮00A2−10⋮000A3−1⋮0⋯⋯⋯⋱⋯000⋮Ak−1 (b) ##### 证明 对角分块矩阵的逆可以通过验证 AA−1=IA A\^{-1} = IAA−1=I 来证明。由于矩阵的分块结构,有: AA−1=\[A1A1−10⋯00A2A2−1⋯0⋮⋮⋱⋮00⋯AkAk−1\]=\[I10⋯00I2⋯0⋮⋮⋱⋮00⋯Ik\]=I A A\^{-1} = \\begin{bmatrix} A_1 A_1\^{-1} \& 0 \& \\cdots \& 0 \\\\ 0 \& A_2 A_2\^{-1} \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& \\cdots \& A_k A_k\^{-1} \\end{bmatrix} = \\begin{bmatrix} I_1 \& 0 \& \\cdots \& 0 \\\\ 0 \& I_2 \& \\cdots \& 0 \\\\ \\vdots \& \\vdots \& \\ddots \& \\vdots \\\\ 0 \& 0 \& \\cdots \& I_k \\end{bmatrix} = I AA−1= A1A1−10⋮00A2A2−1⋮0⋯⋯⋱⋯00⋮AkAk−1 = I10⋮00I2⋮0⋯⋯⋱⋯00⋮Ik =I 其中 IiI_iIi 是相应维数的单位矩阵。因此, AAA 的逆矩阵为(b)式。 *** ** * ** *** 乘以左边第一个矩阵的逆矩阵,得 V′=\[e−jθ10e−jθ2⋱0e−jθN\]S\[e−jθ10e−jθ2⋱0e−jθN\]V′+ V' = \\begin{bmatrix} e\^{-j\\theta_1} \&\&\& 0 \\\\ \& e\^{-j\\theta_2} \& \\\\ \&\&\\ddots \& \\\\ 0 \&\&\& e\^{-j\\theta_N} \\\\ \\end{bmatrix} S \\begin{bmatrix} e\^{-j\\theta_1} \& 0 \\\\ \&e\^{-j\\theta_2} \& \\\\ \&\&\\ddots \& \\\\ 0 \& \&\&e\^{-j\\theta_N} \\\\ \\end{bmatrix} V\^{\\prime+} V′= e−jθ10e−jθ2⋱0e−jθN S e−jθ100e−jθ2⋱e−jθN V′+ 与式(4.54b)对比,有 S′=\[e−jθ10e−jθ2⋱0e−jθN\]S\[e−jθ10e−jθ2⋱0e−jθN\](4.56) S' = \\begin{bmatrix} e\^{-j\\theta_1} \& \&\&0 \\\\ \&e\^{-j\\theta_2} \& \\\\ \&\&\\ddots \& \\\\ 0 \&\&\& e\^{-j\\theta_N} \\\\ \\end{bmatrix} S \\begin{bmatrix} e\^{-j\\theta_1} \& \&\&0 \\\\ \&e\^{-j\\theta_2} \& \\\\ \&\&\\ddots \& \\\\ 0 \& \&\&e\^{-j\\theta_N} \\\\ \\end{bmatrix} \\quad (4.56) S′= e−jθ10e−jθ2⋱0e−jθN S e−jθ10e−jθ2⋱0e−jθN (4.56) 该变换反映了参考平面移动时散射矩阵的相位修正:**每个端口移动的电长度θi=βiℓi\\theta_i = \\beta_i \\ell_iθi=βiℓi 导致入射波相位增加θi\\theta_iθi,反射波相位减少 θi\\theta_iθi,因此散射矩阵元素SijS_{ij}Sij变为 e−jθiSije−jθje\^{-j\\theta_i} S_{ij} e\^{-j\\theta_j}e−jθiSije−jθj**。这就是想要的结果。注意,Snn′=e−2jθnSnnS'_{nn} = e\^{-2j\\theta_n} S_{nn}Snn′=e−2jθnSnn意味着SnnS_{nn}Snn的相移是端平面n移动的电长度的2倍,这是因为波在入射和反射时,行进的距离是该长度的2倍。这一结果与式(2.42)一致,后者给出了参考平面移动导致的传输线上的反射系数变化。 ### 4.3.3 功率波和广义散射参量 前面已将传输线上的**总电压和总电流** 表示为**入射电压波振幅和反射电压波振幅**的函数,如式(2.34)或式(4.42)所示: V=V0++V0−(4.57a) V = V_0\^{+} + V_0\^{-} \\quad (4.57a) V=V0++V0−(4.57a) I=1Z0(V0+−V0−)(4.57b) I = \\frac{1}{Z_0} (V_0\^{+} - V_0\^{-}) \\quad (4.57b) I=Z01(V0+−V0−)(4.57b) 式中,Z0Z_0Z0是传输线的特征阻抗。整理式(4.57),得到入射电压和反射电压波振幅,它们是总电压和电流的函数: V0+=V+Z0I2(4.58a) V_0\^{+} = \\frac{V + Z_0 I}{2} \\quad (4.58a) V0+=2V+Z0I(4.58a) V0−=V−Z0I2(4.58b) V_0\^{-} = \\frac{V - Z_0 I}{2} \\quad (4.58b) V0−=2V−Z0I(4.58b) 传送到负载的平均功率为 PL=12(V0++V0−)⋅\[1Z0(V0+−V0−)\]∗ P_L = \\frac{1}{2} (V_0\^+ + V_0\^-) \\cdot \\left\[ \\frac{1}{Z_0} (V_0\^+ - V_0\^-) \\right\]\^\* PL=21(V0++V0−)⋅\[Z01(V0+−V0−)\]∗ 注意电流的共轭: I∗=(1Z0(V0+−V0−))∗=1Z0∗(V0+∗−V0−∗) I\^\* = \\left( \\frac{1}{Z_0} (V_0\^+ - V_0\^-) \\right)\^\* = \\frac{1}{Z_0\^\*} (V_0\^{+\*} - V_0\^{-\*}) I∗=(Z01(V0+−V0−))∗=Z0∗1(V0+∗−V0−∗) **这里假定是无耗传输线Z0Z_0Z0 是实数,所以Z0∗=Z0Z_0\^\* = Z_0Z0∗=Z0。** Z0=R+jωLγ=R+jωLG+jωC=L/C(2.13) Z_{0} = \\frac{R+\\mathrm{j} \\omega L}{\\gamma} = \\sqrt{\\frac{R+\\mathrm{j} \\omega L}{G+\\mathrm{j} \\omega C}} = \\sqrt{L / C} \\quad (2.13) Z0=γR+jωL=G+jωCR+jωL =L/C (2.13) 代入得: PL=12(V0++V0−)⋅1Z0(V0+∗−V0−∗)=12Z0(V0++V0−)(V0+∗−V0−∗) P_L = \\frac{1}{2} (V_0\^+ + V_0\^-) \\cdot \\frac{1}{Z_0} (V_0\^{+\*} - V_0\^{-\*}) \\\\= \\frac{1}{2Z_0} (V_0\^+ + V_0\^-)(V_0\^{+\*} - V_0\^{-\*}) PL=21(V0++V0−)⋅Z01(V0+∗−V0−∗)=2Z01(V0++V0−)(V0+∗−V0−∗) 展开括号中的乘积: (V0++V0−)(V0+∗−V0−∗)=V0+V0+∗−V0+V0−∗+V0−V0+∗−V0−V0−∗ (V_0\^+ + V_0\^-)(V_0\^{+\*} - V_0\^{-\*}) \\\\= V_0\^+ V_0\^{+\*} - V_0\^+ V_0\^{-\*} + V_0\^- V_0\^{+\*} - V_0\^- V_0\^{-\*} (V0++V0−)(V0+∗−V0−∗)=V0+V0+∗−V0+V0−∗+V0−V0+∗−V0−V0−∗ 其中 V0+V0+∗=∣V0+∣2和V0−V0−∗=∣V0−∣2 V_0\^+ V_0\^{+\*} = \|V_0\^+\|\^2 \\quad \\text{和} \\quad V_0\^- V_0\^{-\*} = \|V_0\^-\|\^2 V0+V0+∗=∣V0+∣2和V0−V0−∗=∣V0−∣2 PL=12Re{VI∗}=12Z0Re{∣V0+∣2−V0+V0−∗+V0+∗V0−−∣V0−∣2}=12Z0(∣V0+∣2−∣V0−∣2)(4.59) \\begin{aligned} P_{L}\&=\\frac{1}{2} \\operatorname{Re}\\left\\{V I\^{\*}\\right\\}=\\frac{1}{2 Z_{0}} \\operatorname{Re}\\left\\{\\left\|V_{0}\^{+}\\right\|\^{2}-V_{0}\^{+} V_{0}\^{-\*}+V_{0}\^{+\*} V_{0}\^{-}-\\left\|V_{0}\^{-}\\right\|\^{2}\\right\\} \\\\ \&=\\frac{1}{2 Z_{0}}\\left(\\left\|V_{0}\^{+}\\right\|\^{2}-\\left\|V_{0}\^{-}\\right\|\^{2}\\right) \\quad (4.59) \\end{aligned} PL=21Re{VI∗}=2Z01Re{ V0+ 2−V0+V0−∗+V0+∗V0−− V0− 2}=2Z01( V0+ 2− V0− 2)(4.59) > 负载吸收的平均功率等于入射波功率减去反射波功率。入射波和反射波之间的相互作用(交叉项)只贡献**无功功率** (虚部),对**实功率** (有功功率)没有贡献。这是因为入射波和反射波是反向传播的,它们的相互作用不产生净能量传输。如果负载完全匹配V0−=0V_0\^- = 0V0−=0,PL=PV0+=12Z0(∣V0+∣2)P_{L}=P_{V_{0}\^{+}}=\\frac{1}{2 Z_{0}}\\left(\\left\|V_{0}\^{+}\\right\|\^{2}\\right)PL=PV0+=2Z01( V0+ 2)则全部入射功率被负载吸收;如果全反射(∣V0−∣=∣V0+∣\|V_0\^-\| = \|V_0\^+\|∣V0−∣=∣V0+∣),则净功率PL=0P_{L}=0PL=0。这个结果是传输线理论的基本结论,也是实际测量中通过测量入射波和反射波幅度来计算负载功率的基础。 > > 最后一个等式成立的原因是**V0+V0−∗−V0+∗V0−V_{0}\^{+} V_{0}\^{-\*}-V_{0}\^{+\*} V_{0}\^{-}V0+V0−∗−V0+∗V0−两者互为共轭标量,做差是纯虚数**。这是物理上令人满意的结果,因为它表示的是当入射功率和反射功率不同时,发送到负载的净功率。遗憾的是,**这一结果仅在特征阻抗是实数时有效,Z0Z_{0}Z0是复数时则不适用,因为此时是有耗线。**此外,当信号源和负载之间**无传输线时,这些结果是没有用的** ,如图4.10中的电路所示。 > 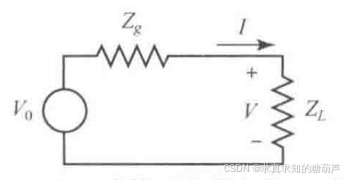 > 图4.10阻抗Zg的信号源连接到负载阻抗ZL > #### 功率波定义 在图4.10所示的电路中,因为由集总元件组成,没有传输线,所以**既没有定义的特征阻抗Z0Z_0Z0,也没有电压反射系数Γ\\GammaΓ,甚至没有入射/反射电压波或电流波** 。然而,定义一种称为**功率波的新波是可行的,功率波在处理信号源和负载之间的功率传输时很有用,它既适用于图4.10中的一般电路,也适用于无耗或有耗传输线问题。**下面介绍如何由功率波导出通用的散射参量。 入射和反射功率波振幅a和b可定义为电压和电流的如下**线性变换** **(推广)**: > 功率表达式简洁统一为P=12(∣a∣2−∣b∣2)P = \\frac{1}{2}(\|a\|\^2 - \|b\|\^2)P=21(∣a∣2−∣b∣2),物理意义清晰,**a** 和 **b** 的模平方直接对应功率,兼容复数参考阻抗,并退化为实数特性阻抗的传统情况,为广义散射矩阵理论提供方便的数学形式,便于分析和计算。 V0+=V+Z0I2,V0−=V−Z0I2(4.58) V_0\^{+} = \\frac{V + Z_0 I}{2} ,\\quad V_0\^{-} = \\frac{V - Z_0 I}{2} \\quad (4.58) V0+=2V+Z0I,V0−=2V−Z0I(4.58) a=V+ZRI2RR(4.60a),b=V−ZR∗I2RR(4.60b) a=\\frac{V+Z_{R} I}{2 \\sqrt{R_{R}}} \\quad (4.60a), b=\\frac{V-Z_{R}\^{\*} I}{2 \\sqrt{R_{R}}} \\quad (4.60b) a=2RR V+ZRI(4.60a),b=2RR V−ZR∗I(4.60b) 式中,**ZR=RR+jXRZ_{R}=R_{R}+j X_{R}ZR=RR+jXR称为参考阻抗,它可以是复数。**注意,式(4.60)中功率波振幅的形式类似于式(4.58)中的电压波,但**没有功率、电压或电流**的单位。 整理式(4.60)可得总电压和电流,它们是功率波振幅的函数: a−b=2RRI2RR=RRIRR=IRR a - b = \\frac{2 R_R I}{2 \\sqrt{R_R}} = \\frac{R_R I}{\\sqrt{R_R}} = I \\sqrt{R_R} a−b=2RR 2RRI=RR RRI=IRR V=ZR∗a+ZRbRR(4.61a) V=\\frac{Z_{R}\^{\*} a+Z_{R} b}{\\sqrt{R_{R}}} \\quad (4.61a) V=RR ZR∗a+ZRb(4.61a) I=a−bRR(4.61b) I=\\frac{a-b}{\\sqrt{R_{R}}} \\quad (4.61b) I=RR a−b(4.61b) 因此,传送到负载的功率为 PL=12Re{VI∗}=12RRRe{ZR∗∣a∣2−ZR∗ab∗+ZRa∗b−ZR∣b∣2}=12∣a∣2−12∣b∣2(4.62) \\begin{aligned} P_{L}\&=\\frac{1}{2} \\operatorname{Re}\\left\\{V I\^{\*}\\right\\}=\\frac{1}{2 R_{R}} \\operatorname{Re}\\left\\{Z_{R}\^{\*}\|a\|\^{2}-Z_{R}\^{\*} a b\^{\*}+Z_{R} a\^{\*} b-Z_{R}\|b\|\^{2}\\right\\} \\\\ \&=\\frac{1}{2}\|a\|\^{2}-\\frac{1}{2}\|b\|\^{2} \\quad (4.62) \\end{aligned} PL=21Re{VI∗}=2RR1Re{ZR∗∣a∣2−ZR∗ab∗+ZRa∗b−ZR∣b∣2}=21∣a∣2−21∣b∣2(4.62) **类似的因为ZRa∗b−ZR∗ab∗Z_{R} a\^{\*} b-Z_{R}\^{\*} a b\^{\*}ZRa∗b−ZR∗ab∗前后两项互为共轭标量,做差是纯虚数,**这里再次得到了令人满意的结果,即**负载功率是入射功率波和反射功率波的功率之差。注意,该结果适用于任何参考阻抗ZRZ_{R}ZR。** #### 最小反射条件 使用式(4.60)和V=ZLIV=Z_{L} IV=ZLI,可求得负载处的反射功率波的反射系数Γp\\Gamma_{p}Γp: Γp=ba=V−ZR∗IV+ZRI=ZL−ZR∗ZL+ZR(4.63) \\Gamma_{p}=\\frac{b}{a}=\\frac{V-Z_{R}\^{\*} I}{V+Z_{R} I}=\\frac{Z_{L}-Z_{R}\^{\*}}{Z_{L}+Z_{R}} \\quad (4.63) Γp=ab=V+ZRIV−ZR∗I=ZL+ZRZL−ZR∗(4.63) 观察发现,当ZR=Z0Z_{R}=Z_{0}ZR=Z0时,这个反射系数就简化为通常使用的电压反射系数公式(2.35)。式(4.63)表明,当**参考阻抗**选为负载阻抗的共轭\[5\],即 ZR=ZL∗(4.64) Z_{R}=Z_{L}\^{\*} \\quad (4.64) ZR=ZL∗(4.64) Γp=ba=V−ZR∗IV+ZRI=ZL−(ZL∗)∗ZL+ZR=0 \\Gamma_{p}=\\frac{b}{a}=\\frac{V-Z_{R}\^{\*} I}{V+Z_{R} I}=\\frac{Z_{L}-(Z_{L}\^{\*})\^{\*}}{Z_{L}+Z_{R}}=0Γp=ab=V+ZRIV−ZR∗I=ZL+ZRZL−(ZL∗)∗=0 > 将得到非常有用的结果,**此时反射功率波的幅度为零,这在广义散射参数分析中通常更有用,因为它能简化端口描述(每个端口反射为零)。** (有些作者选择让参考阻抗等于信号源阻抗。**当信号源和负载共轭匹配时,这与式(4.64)的效果相同。如果不匹配时,虽然满足最大功率传输条件,但是反射波不为零**)  由基本电路理论可知,图4.10所示电路的电压、电流和负载功率为 V=V0ZLZL+Zg,I=V0ZL+Zg,PL=V022RL∣ZL+Zg∣2(4.65a,b,c) V=V_{0}\\frac{Z_{L}}{Z_{L}+Z_{g}}, \\quad I=\\frac{V_{0}}{Z_{L}+Z_{g}}, \\quad P_{L}=\\frac{V_{0}\^{2}}{2}\\frac{R_{L}}{\\left\|Z_{L}+Z_{g}\\right\|\^{2}} \\quad (4.65a, b, c) V=V0ZL+ZgZL,I=ZL+ZgV0,PL=2V02∣ZL+Zg∣2RL(4.65a,b,c) 式中,ZL=RL+jXLZ_{L}=R_{L}+\\mathrm{j} X_{L}ZL=RL+jXL。因此,当ZR=ZL∗Z_{R}=Z_{L}\^{\*}ZR=ZL∗时,由式(4.60)可得功率波振幅为 a=V+ZRI2RR=V0ZLZL+Zg+ZL∗ZL+Zg2RR=V0RLZL+Zg(4.66a) a=\\frac{V+Z_{R} I}{2 \\sqrt{R_{R}}}=V_{0} \\frac{\\frac{Z_{L}}{Z_{L}+Z_{g}}+\\frac{Z_{L}\^{\*}}{Z_{L}+Z_{g}}}{2 \\sqrt{R_{R}}}=V_{0} \\frac{\\sqrt{R_{L}}}{Z_{L}+Z_{g}} \\quad (4.66a) a=2RR V+ZRI=V02RR ZL+ZgZL+ZL+ZgZL∗=V0ZL+ZgRL (4.66a) b=V−ZR∗I2RR=V0ZLZL+Zg−ZLZL+Zg2RR=0(4.66b) b=\\frac{V-Z_{R}\^{\*} I}{2 \\sqrt{R_{R}}}=V_{0} \\frac{\\frac{Z_{L}}{Z_{L}+Z_{g}}-\\frac{Z_{L}}{Z_{L}+Z_{g}}}{2 \\sqrt{R_{R}}}=0 \\quad (4.66b) b=2RR V−ZR∗I=V02RR ZL+ZgZL−ZL+ZgZL=0(4.66b) #### 最大功率传输条件 由式(4.62)可得传送到负载的功率为 PL=12∣a∣2=V022RL∣ZL+Zg∣2 P_{L}=\\frac{1}{2}\|a\|\^{2}=\\frac{V_{0}\^{2}}{2} \\frac{R_{L}}{\\left\|Z_{L}+Z_{g}\\right\|\^{2}} PL=21∣a∣2=2V02∣ZL+Zg∣2RL Zg+ZL=(Rg+RL)+j(Xg+XL) Z_g + Z_L = (R_g + R_L) + j(X_g + X_L) Zg+ZL=(Rg+RL)+j(Xg+XL) 模平方: ∣Zg+ZL∣2=(Rg+RL)2+(Xg+XL)2 \|Z_g + Z_L\|\^2 = (R_g + R_L)\^2 + (X_g + X_L)\^2 ∣Zg+ZL∣2=(Rg+RL)2+(Xg+XL)2 PL=12∣V0∣2RL(Rg+RL)2+(Xg+XL)2 P_L = \\frac{1}{2} \|V_0\|\^2 \\frac{R_L}{(R_g + R_L)\^2 + (X_g + X_L)\^2} PL=21∣V0∣2(Rg+RL)2+(Xg+XL)2RL 为最大化PLP_LPL,首先固定RLR_LRL,调整XLX_LXL。显然,当XL=−XgX_L = -X_gXL=−Xg时,分母中的(Xg+XL)2=0(X_g + X_L)\^2 = 0(Xg+XL)2=0,此时: PL=12∣V0∣2RL(Rg+RL)2 P_L = \\frac{1}{2} \|V_0\|\^2 \\frac{R_L}{(R_g + R_L)\^2} PL=21∣V0∣2(Rg+RL)2RL 再对RLR_LRL 求导(V0V_0V0 和RgR_gRg为常数): dPLdRL=12∣V0∣2⋅(Rg+RL)2−2RL(Rg+RL)(Rg+RL)4=12∣V0∣2⋅Rg2−RL2(Rg+RL)4 \\frac{dP_L}{dR_L} = \\frac{1}{2} \|V_0\|\^2 \\cdot \\frac{(R_g + R_L)\^2 - 2R_L(R_g + R_L)}{(R_g + R_L)\^4} \\\\= \\frac{1}{2} \|V_0\|\^2 \\cdot \\frac{R_g\^2 - R_L\^2}{(R_g + R_L)\^4} dRLdPL=21∣V0∣2⋅(Rg+RL)4(Rg+RL)2−2RL(Rg+RL)=21∣V0∣2⋅(Rg+RL)4Rg2−RL2 令导数为零,得Rg2−RL2=0R_g\^2 - R_L\^2 = 0Rg2−RL2=0,即RL=RgR_L = R_gRL=Rg(取正值)。容易判断一阶导数在零点前后符号相反,所以为极大值。 **当负载与信号源共轭匹配时,Zg=ZL∗Z_{g}=Z_{L}\^{\*}Zg=ZL∗,有PL=V02/8RLP_{L}=V_{0}\^{2}/8R_{L}PL=V02/8RL。**将参考阻抗选为ZR=ZL∗Z_{R}=Z_{L}\^{\*}ZR=ZL∗可以满足条件b=0b=0b=0(**参考阻抗与负载阻抗共轭无反射** )(和Γp=0\\Gamma_{p}=0Γp=0),但这并不表示负载与信号源是共轭匹配的,又不表示最大功率会传送到负载。式(4.66a)中的入射功率波振幅取决于ZLZ_{L}ZL和ZgZ_{g}Zg,仅在Zg=ZL∗Z_{g}=Z_{L}\^{\*}Zg=ZL∗时最大。 #### **功率波广义散射矩阵** **对N端口网络定义功率波的散射矩阵**,假设端口i的参考阻抗为ZRiZ_{Ri}ZRi。 在多端口网络中,各端口可能有不同的参考阻抗(可为复数)。定义对角矩阵: ZR=diag(ZR1,ZR2,...,ZRN) \\mathbf{Z}_R = \\operatorname{diag}(Z_{R1}, Z_{R2}, \\dots, Z_{RN}) ZR=diag(ZR1,ZR2,...,ZRN) F=diag(12RR1,12RR2,...,12RRN) \\mathbf{F} = \\operatorname{diag}\\left(\\frac{1}{2\\sqrt{R_{R1}}}, \\frac{1}{2\\sqrt{R_{R2}}}, \\dots, \\frac{1}{2\\sqrt{R_{RN}}}\\right) F=diag(2RR1 1,2RR2 1,...,2RRN 1) 因此,类似于式a=V+ZRI2RR,b=V−ZR∗I2RRa=\\frac{V+Z_{R} I}{2 \\sqrt{R_{R}}} , b=\\frac{V-Z_{R}\^{\*} I}{2 \\sqrt{R_{R}}}a=2RR V+ZRI,b=2RR V−ZR∗I,可将功率波振幅向量定义为包含所有电压和电流的向量的函数: a=F(V+ZRI)(4.67a) a=F\\left(V+Z_{R} I\\right) \\quad (4.67a) a=F(V+ZRI)(4.67a) b=F(V−ZR∗I)(4.67b) b=F\\left(V-Z_{R}\^{\*} I\\right) \\quad (4.67b) b=F(V−ZR∗I)(4.67b) *** ** * ** *** 式中,F是元素为1/2Re{ZRi}1/2\\sqrt{\\operatorname{Re}\\left\\{Z_{Ri}\\right\\}}1/2Re{ZRi} 的对角阵(**用于归一化,表达式统一** ),ZRZ_{R}ZR是元素为ZRiZ_{Ri}ZRi的对角阵。根据阻抗矩阵关系V=ZIV=Z IV=ZI,式(4.67)可以写为 由式(4.67a): a=F(ZI+ZRI)=F(Z+ZR)I(a) \\mathbf{a} = \\mathbf{F}(\\mathbf{Z} \\mathbf{I} + \\mathbf{Z}_R \\mathbf{I}) = \\mathbf{F}(\\mathbf{Z} + \\mathbf{Z}_R) \\mathbf{I} \\quad (a) a=F(ZI+ZRI)=F(Z+ZR)I(a) 由式(4.67b): b=F(ZI−ZR∗I)=F(Z−ZR∗)I(b) \\mathbf{b} = \\mathbf{F}(\\mathbf{Z} \\mathbf{I} - \\mathbf{Z}_R\^\* \\mathbf{I}) = \\mathbf{F}(\\mathbf{Z} - \\mathbf{Z}_R\^\*) \\mathbf{I} \\quad (b) b=F(ZI−ZR∗I)=F(Z−ZR∗)I(b) F\\mathbf{F}F对角线元素假设非零,矩阵可逆,同时假设Z+ZR∗\\mathbf{Z} +\\mathbf{Z}_R\^\*Z+ZR∗可逆,(a)式左乘F−1\\mathbf{F}\^{-1}F−1: F−1a=(Z+ZR)I \\mathbf{F}\^{-1} \\mathbf{a} = (\\mathbf{Z} + \\mathbf{Z}_R) \\mathbf{I} F−1a=(Z+ZR)I 解得: I=(Z+ZR)−1F−1a(c) \\mathbf{I} = (\\mathbf{Z} + \\mathbf{Z}_R)\^{-1} \\mathbf{F}\^{-1} \\mathbf{a} \\quad (c) I=(Z+ZR)−1F−1a(c) 将式(c)(c)(c)代入式(b)得: b=F(Z−ZR∗)I=F(Z−ZR∗)(Z+ZR)−1F−1a \\begin{aligned} \\mathbf{b} \&= \\mathbf{F}(\\mathbf{Z} - \\mathbf{Z}_R\^\*) \\mathbf{I} \\\\ \&= \\mathbf{F}(\\mathbf{Z} - \\mathbf{Z}_R\^\*) (\\mathbf{Z} + \\mathbf{Z}_R)\^{-1} \\mathbf{F}\^{-1} \\mathbf{a} \\end{aligned} b=F(Z−ZR∗)I=F(Z−ZR∗)(Z+ZR)−1F−1a 根据散射矩阵的定义 b=Spa\\mathbf{b} = \\mathbf{S}_p \\mathbf{a}b=Spa,由上式可得: Sp=F(Z−ZR∗)(Z+ZR)−1F−1(4.68) S_{p}=F\\left(Z-Z_{R}\^{\*}\\right)\\left(Z+Z_{R}\\right)\^{-1} F\^{-1} \\quad (4.68) Sp=F(Z−ZR∗)(Z+ZR)−1F−1(4.68) > **特殊情况** 验证 > > 当所有端口参考阻抗相同且为实数 ZRi=Z0Z_{Ri} = Z_0ZRi=Z0(实数)时: > ZR=Z0E\\mathbf{Z}_R = Z_0 \\mathbf{E}ZR=Z0E,ZR∗=Z0E\\mathbf{Z}_R\^\* = Z_0 \\mathbf{E}ZR∗=Z0E,F=12Z0E\\mathbf{F} = \\frac{1}{2\\sqrt{Z_0}} \\mathbf{E}F=2Z0 1E > > 代入式(4.68): > Sp=12Z0E(Z−Z0E)(Z+Z0E)−1(2Z0E)=(Z−Z0E)(Z+Z0E)−1 \\mathbf{S}_p = \\frac{1}{2\\sqrt{Z_0}} \\mathbf{E} (\\mathbf{Z} - Z_0 \\mathbf{E}) (\\mathbf{Z} + Z_0 \\mathbf{E})\^{-1} (2\\sqrt{Z_0} \\mathbf{E}) \\\\=(\\mathbf{Z} - Z_0 \\mathbf{E})(\\mathbf{Z} + Z_0 \\mathbf{E})\^{-1} Sp=2Z0 1E(Z−Z0E)(Z+Z0E)−1(2Z0 E)=(Z−Z0E)(Z+Z0E)−1 > > 这与**上集我们推的传统的散射矩阵(归一化电压波)(4.44)形式一致(Z0=1Z_0=1Z0=1),验证了广义公式的正确性。** > **广义散射矩阵** Sp\\mathbf{S}_pSp 将入射功率波a\\mathbf{a}a与反射功率波b\\mathbf{b}b联系起来。当各端口参考阻抗不同(可为复数)时,仍能保持功率波的简洁功率关系 P=12(aHa−bHb)(H为转置共轭运算)P = \\frac{1}{2}(\\mathbf{a}\^H \\mathbf{a} - \\mathbf{b}\^H \\mathbf{b})(H为转置共轭运算)P=21(aHa−bHb)(H为转置共轭运算)式(4.68)提供了从阻抗矩阵Z\\mathbf{Z}Z和任意参考阻抗ZR\\mathbf{Z}_RZR计算广义散射矩阵的方法。 **网络的普通散射矩阵可首先用类似于式(4.45)Z=(E+S)(E−S)−1Z=(E+S)(E-S)\^{-1}Z=(E+S)(E−S)−1的关系式转换为一个阻抗矩阵,然后用式(4.68)转换为通用功率波散射矩阵。**通用散射矩阵的一个有用性质是,正确选择参考阻抗可让对角元素为零。 ### 兴趣点:矢量网络分析仪VNA 矢量网络分析仪可用来测量无源和有源网络的S参量,它是一台双(或四)通道微波接收机,可用来处理来自网络的透射波和反射波的幅值与相位。网络分析仪的简化框图如下图所示。工作时,扫频的高频源通常设在指定的频宽范围内。四端口反射计对入射、反射和透射射频波取样;一个开关可从端口1或端口2激励网络。4个双重转换通道把这些信号变换成100kHz的中频,然后进行检测并转换成数字形式。用功能强大的内置计算机计算并显示出S参量的幅值和相位,或可从S参量导出其他量,如驻波比(SWR)、回波损耗、群时延、阻抗等。该网络分析仪的一个重要特点是,可用误差修正软件提升精度,它使用12个误差模型和校正处理方法来处理因定向耦合器失配、方向性不完善、损耗和分析仪系统的频响变动导致的误差。另一个有用的特性是,能够通过计算频率域数据的傅里叶反变换来确定网络的时域响应。  矢量网络分析仪的简化框图