
一、研究背景
- Stacking 集成学习是一种通过组合多个基学习器的预测结果来提升整体预测性能的方法。
- KAN 是近年来提出的一种新型神经网络结构,基于 Kolmogorov--Arnold 表示定理,使用可学习的激活函数替代固定激活函数,具有较强的函数逼近能力。
- 本代码将传统机器学习模型(PLS、BP、SVM、决策树)与新型 KAN 网络结合,构建了一个两层 Stacking 回归框架,旨在提升回归预测的准确性与鲁棒性。
二、主要功能
- 数据预处理:包括打乱、归一化、训练集/测试集划分。
- 训练四个基学习器 :
- PLS(偏最小二乘回归)
- BP神经网络
- SVM(支持向量机回归)
- 决策树回归
- 构建元学习器数据集:使用基学习器的预测结果作为新特征。
- 训练 KAN 元学习器:对基学习器的输出进行二次学习与融合。
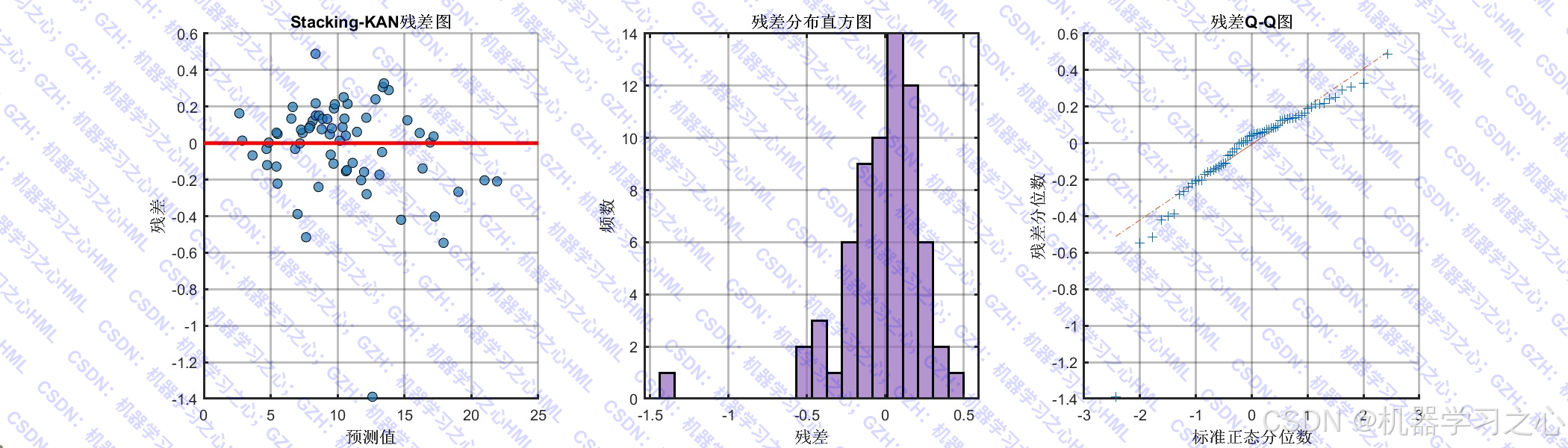
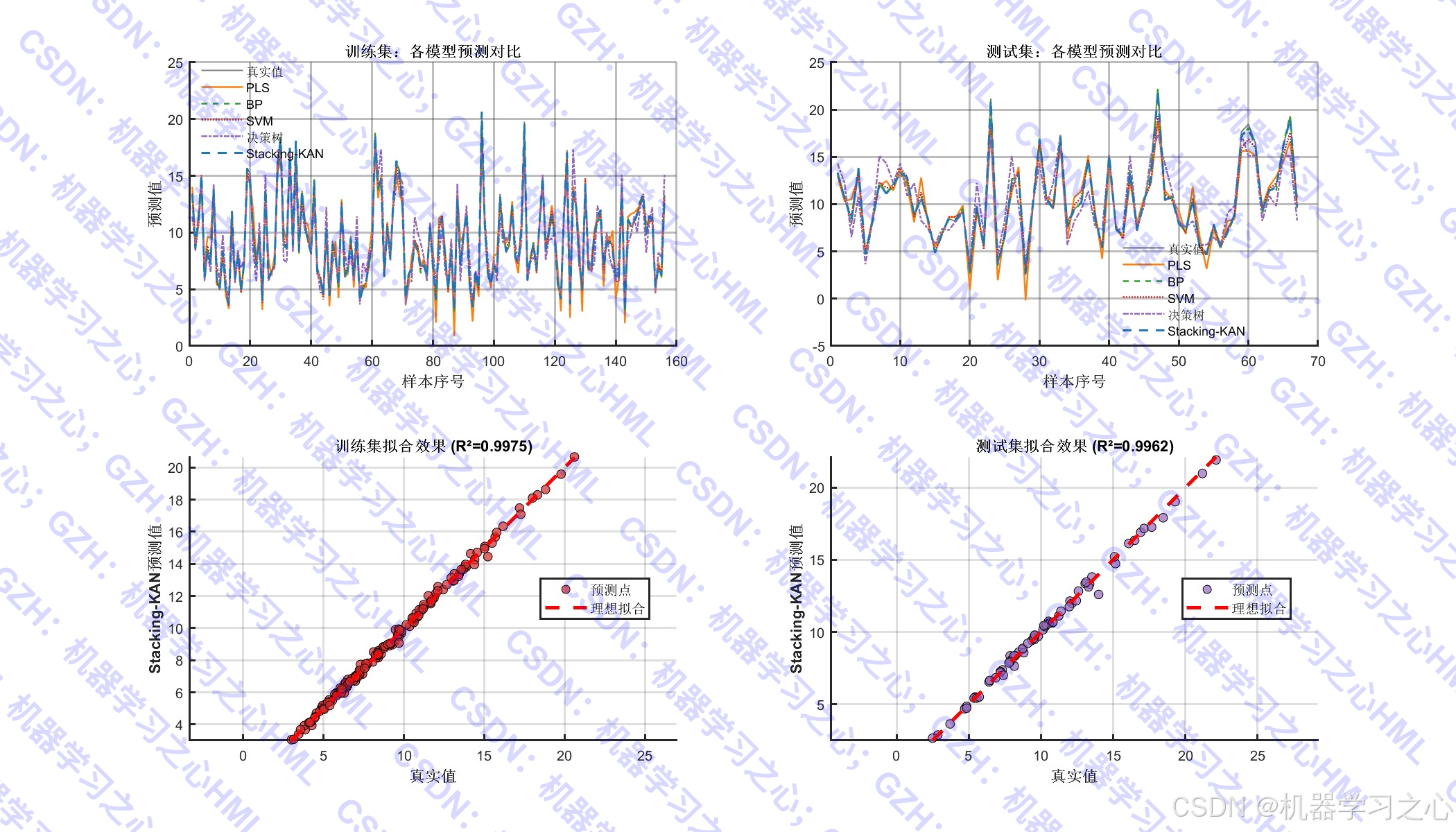
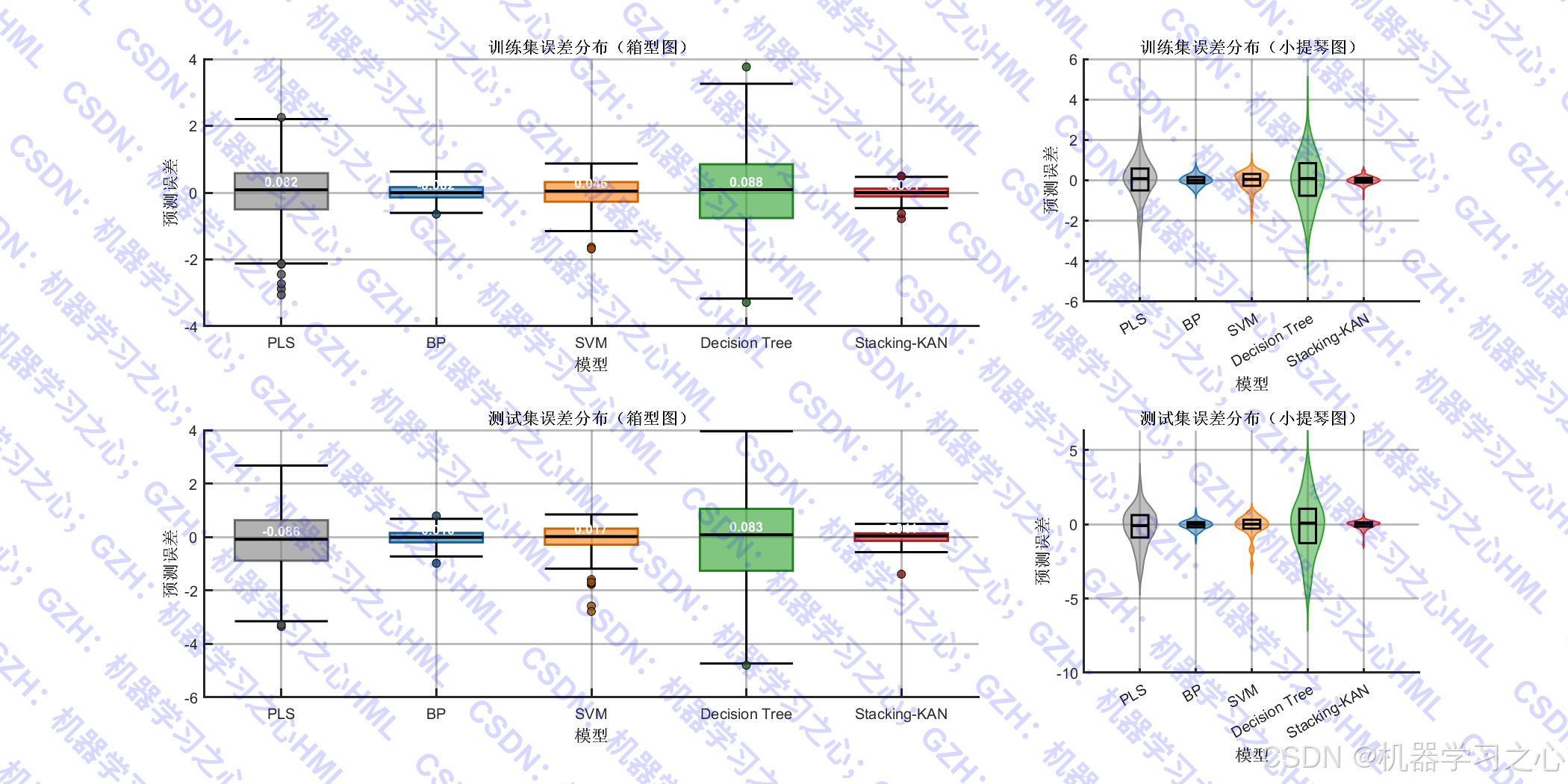
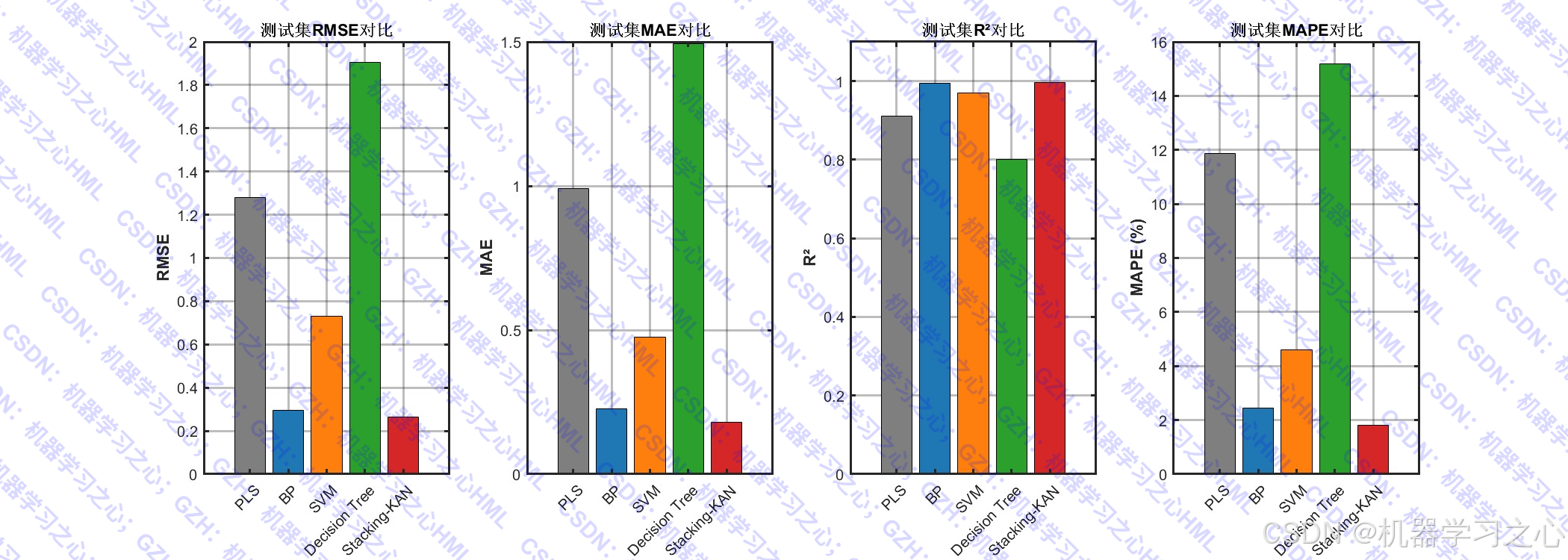
- 模型评估与可视化 :
- 计算 RMSE、MAE、R²、MAPE 等指标
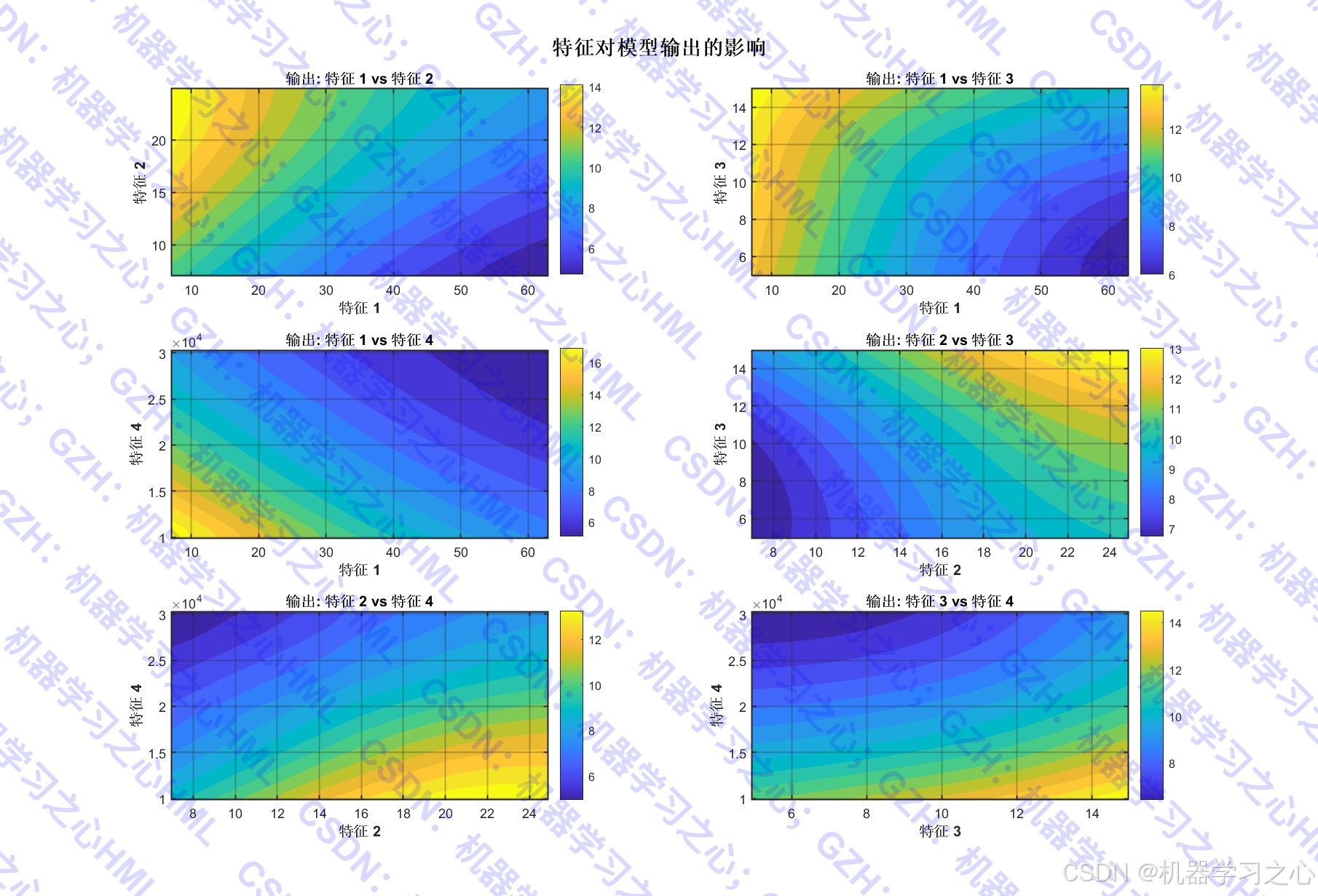
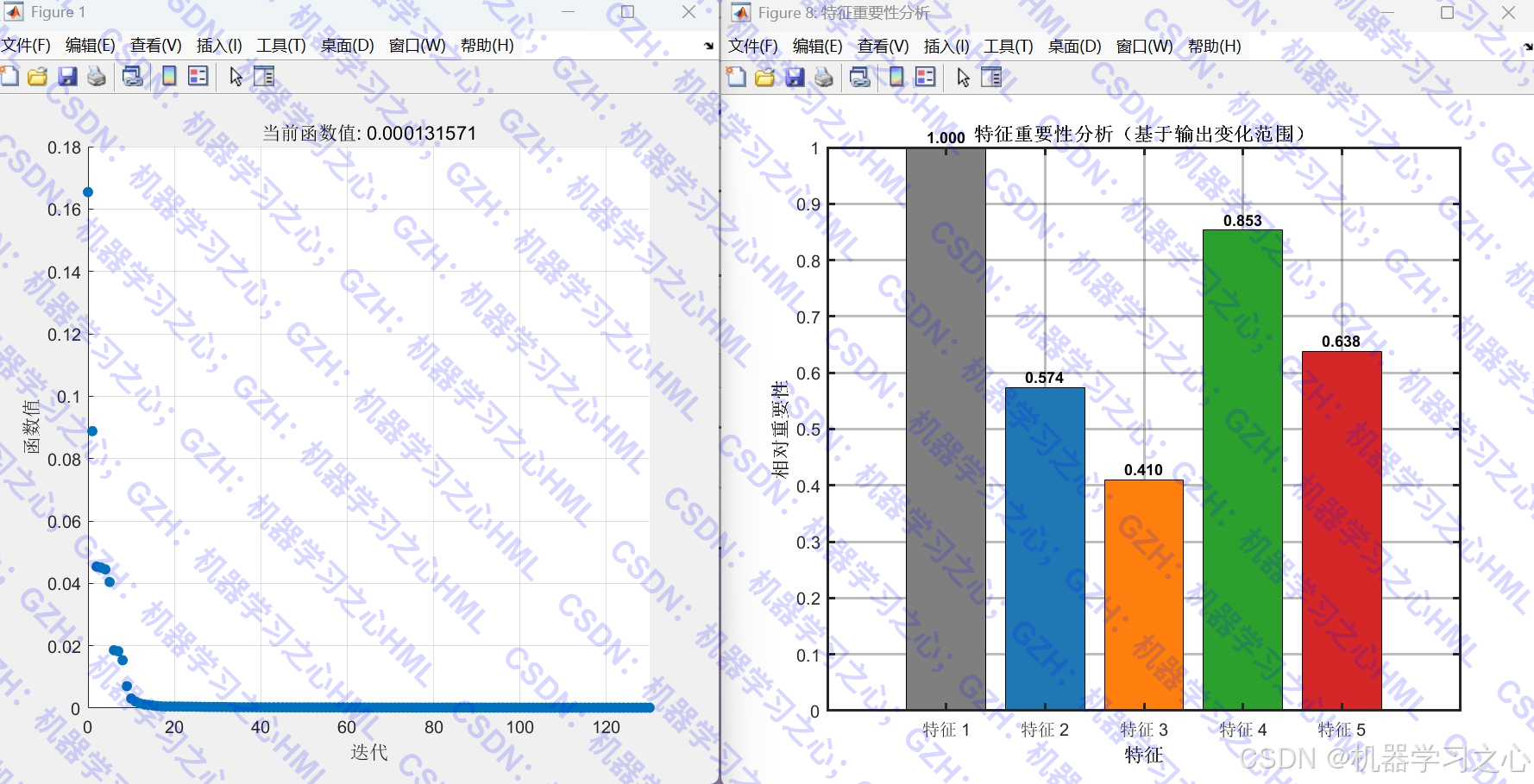
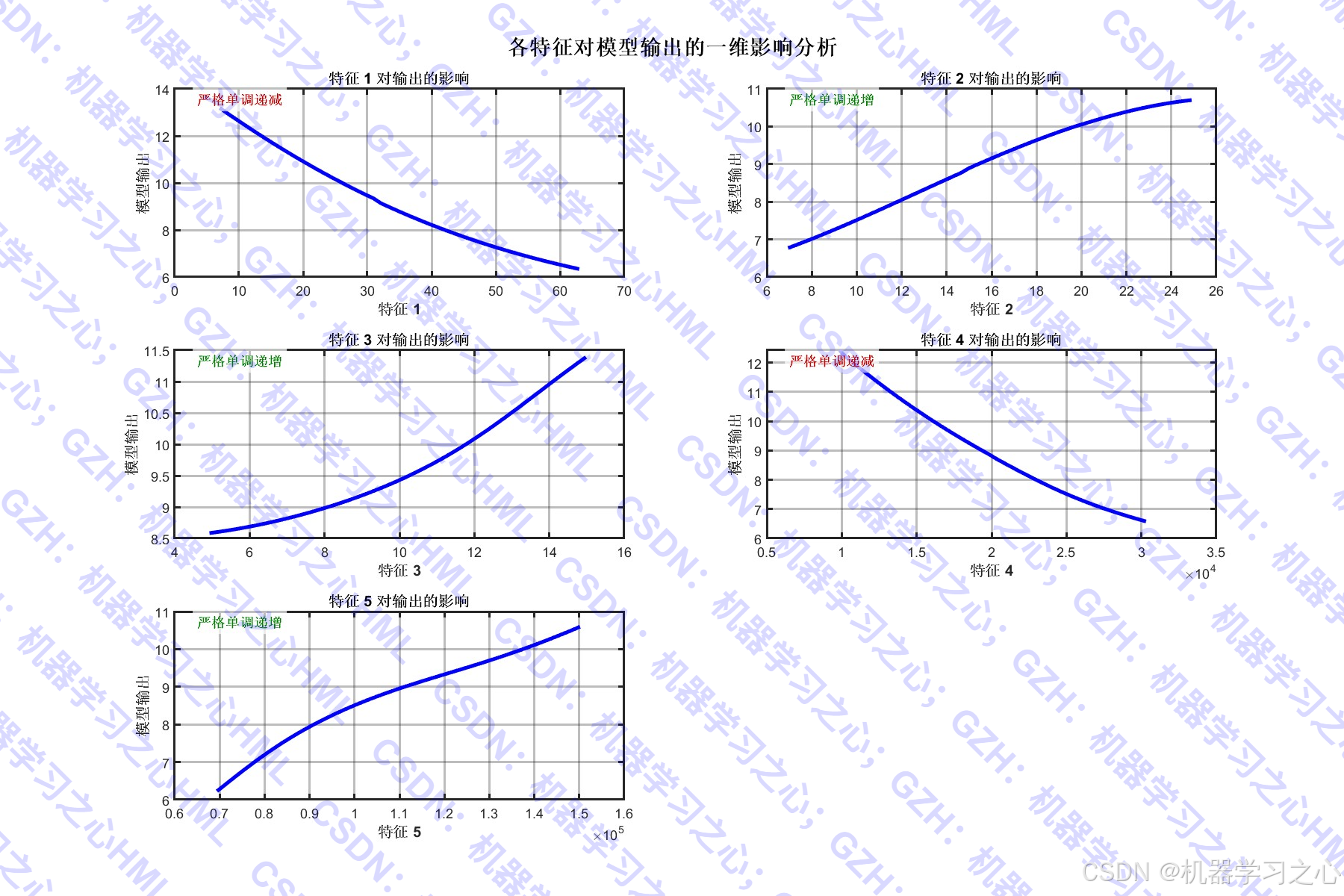
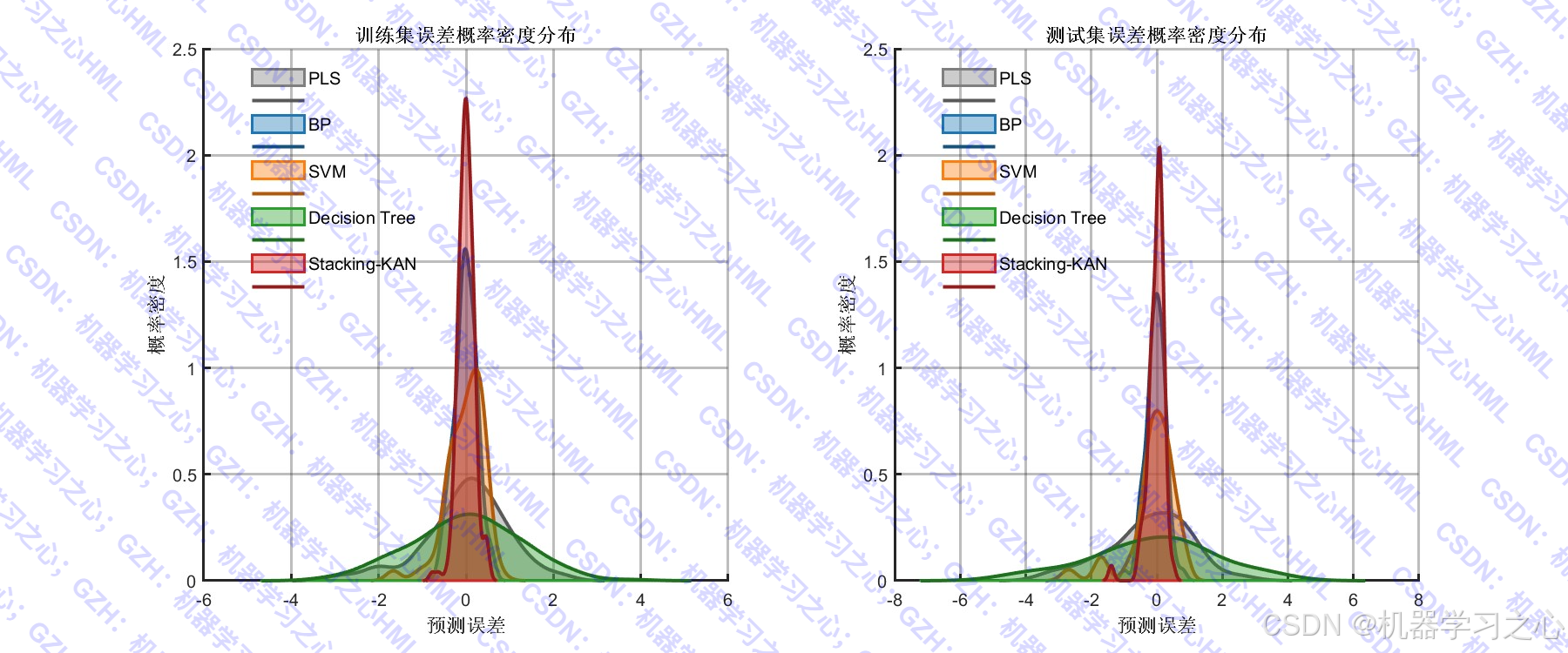
- 绘制预测对比图、误差分布图、特征重要性图、残差分析图等
- 保存模型结果与生成报告。
三、算法步骤
- 导入数据 → 打乱 → 归一化 → 划分训练集/测试集。
- 训练四个基学习器,获取其训练集和测试集的预测结果。
- 将基学习器的预测结果拼接为新的元特征数据集。
- 使用 KAN 网络作为元学习器,对元特征进行训练。
- 使用训练好的 KAN 模型进行预测,并反归一化得到最终结果。
- 评估各模型性能,绘制多种可视化图表。
- 保存模型参数与结果,生成总结报告。
四、技术路线
原始数据 → 预处理 → 基学习器训练(PLS, BP, SVM, Tree)→ 元特征构建 → KAN元学习器 → 预测输出 → 评估与可视化- 采用两层 Stacking 结构,第一层为多个异构基学习器,第二层为 KAN 网络。
- 在元特征中除了基学习器的输出外,还可选择加入原始特征。
五、公式原理
1. Stacking 集成:
y^meta=fKAN(y^PLS,y^BP,y^SVM,y^Tree) \hat{y}{\text{meta}} = f{\text{KAN}}( \hat{y}{\text{PLS}}, \hat{y}{\text{BP}}, \hat{y}{\text{SVM}}, \hat{y}{\text{Tree}} ) y^meta=fKAN(y^PLS,y^BP,y^SVM,y^Tree)
2. KAN 网络:
- 基于 Kolmogorov--Arnold 定理,每个多元函数可表示为:
f(x1,...,xn)=∑q=12n+1Φq(∑p=1nϕq,p(xp)) f(x_1, ..., x_n) = \sum_{q=1}^{2n+1} \Phi_q \left( \sum_{p=1}^n \phi_{q,p}(x_p) \right) f(x1,...,xn)=q=1∑2n+1Φq(p=1∑nϕq,p(xp)) - 代码中使用多项式基函数逼近 (\phi) 和 (\Phi)。
六、参数设定
- 数据划分:训练集 70%,测试集 30%
- PLS :主成分数
ncomp = min(10, 特征数) - BP神经网络 :隐藏层神经元数
hiddenLayerSize = 10,训练轮数epochs = 100 - SVM:使用 RBF 核,参数自动选择或默认设置
- 决策树 :最小叶子节点数
MinLeafSize = 5 - KAN :
- 隐藏层维度
hidden_dim = 8 - 多项式阶数
poly_order = 4 - 正则化参数
lambda = 1e-6, alpha = 1e-6 - 最大迭代次数
max_iter = 200
- 隐藏层维度
七、运行环境
- 软件:MATLAB2020+
- 数据格式 :Excel 文件(
data.xlsx),最后一列为输出变量
八、应用场景
适用于各种回归预测问题,例如:
- 房价预测
- 股票价格预测
- 销量预测
- 工业指标预测
- 气象数据回归