本文参考梁昌洪老师简明微波、RF and Microwave Coupled-Line Circuits和洁仔爱吃冰淇淋的 从耦合微带线到近、远端串扰
1、上节回顾
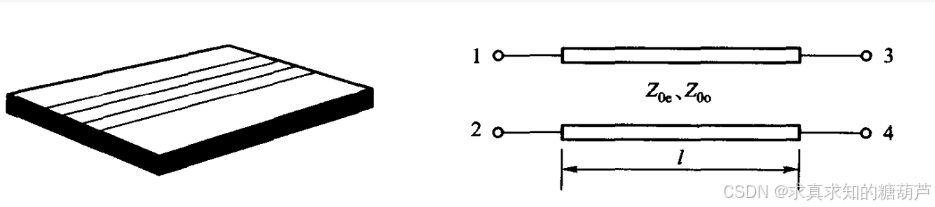
图1:端口顺序定义,1输入,2耦合,3直通(这里2和3与常见定向耦合器不同,想按常见定向耦合器定义将结果交换2与3顺序即可),4隔离
上节我们推导出了对称耦合微带线S参数矩阵
S p = 1 2 [ Γ e + Γ o Γ e − Γ o T e + T o T e − T o Γ e − Γ o Γ e + Γ o T e − T o T e + T o T e + T o T e − T o Γ e + Γ o Γ e − Γ o T e − T o T e + T o Γ e − Γ o Γ e + Γ o ] \mathbf{S}_p = \frac{1}{2} \begin{bmatrix} \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o & T_e + T_o & T_e - T_o \\ \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o & T_e - T_o & T_e + T_o \\ T_e + T_o & T_e - T_o & \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o \\ T_e - T_o & T_e + T_o & \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o \end{bmatrix} Sp=21 Γe+ΓoΓe−ΓoTe+ToTe−ToΓe−ΓoΓe+ΓoTe−ToTe+ToTe+ToTe−ToΓe+ΓoΓe−ΓoTe−ToTe+ToΓe−ΓoΓe+Γo
其中各个参数
Γ e = j ( Z 0 e Z 0 − Z 0 Z 0 e ) sin θ e 2 cos θ e + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin θ e , T e = 2 2 cos θ e + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin θ e \Gamma_e = \frac{j\left(\frac{Z_{0e}}{Z_{0}}-\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e}{2 \cos \theta_e + j\left(\frac{Z_{0e}}{Z_{0}}+\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e}, \quad T_e = \frac{2}{2 \cos \theta_e + j\left(\frac{Z_{0e}}{Z_{0}}+\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e} Γe=2cosθe+j(Z0Z0e+Z0eZ0)sinθej(Z0Z0e−Z0eZ0)sinθe,Te=2cosθe+j(Z0Z0e+Z0eZ0)sinθe2
Γ o = j ( Z 0 o Z 0 − Z 0 Z 0 o ) sin θ o 2 cos θ o + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin θ o , T o = 2 2 cos θ o + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin θ o \Gamma_o = \frac{j\left(\frac{Z_{0o}}{Z_{0}}-\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o}{2 \cos \theta_o + j\left(\frac{Z_{0o}}{Z_{0}}+\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o}, \quad T_o = \frac{2}{2 \cos \theta_o + j\left(\frac{Z_{0o}}{Z_{0}}+\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o} Γo=2cosθo+j(Z0Z0o+Z0oZ0)sinθoj(Z0Z0o−Z0oZ0)sinθo,To=2cosθo+j(Z0Z0o+Z0oZ0)sinθo2
电长度(表示物理长度相对于波长的电气相位延迟) θ \theta θ定义为:
θ = β l = 2 π λ l \theta = \beta l = \frac{2\pi}{\lambda} l θ=βl=λ2πl
当偶模和奇模相速度不相等时,即电长度 θ e ≠ θ o \theta_e \neq \theta_o θe=θo,对四端口网络的匹配和隔离性能有影响。我们可以通过将反射系数 Γ e \Gamma_e Γe和 Γ o \Gamma_o Γo的表达式通分另分子实部虚部为零得到 S 11 = 0 S_{11}=0 S11=0的条件:
2、匹配条件( S 11 = 0 S_{11}=0 S11=0)
为方便计算令 R e = Z 0 e / Z 0 R_e = Z_{0e}/Z_0 Re=Z0e/Z0, R o = Z 0 o / Z 0 R_o = Z_{0o}/Z_0 Ro=Z0o/Z0,则:
Γ e = j ( R e 2 − 1 ) sin θ e 2 R e cos θ e + j ( R e 2 + 1 ) sin θ e , Γ o = j ( R o 2 − 1 ) sin θ o 2 R o cos θ o + j ( R o 2 + 1 ) sin θ o \Gamma_e = \frac{j(R_e^2 - 1) \sin \theta_e}{2R_e \cos \theta_e + j(R_e^2 + 1) \sin \theta_e}, \quad \Gamma_o = \frac{j(R_o^2 - 1) \sin \theta_o}{2R_o \cos \theta_o + j(R_o^2 + 1) \sin \theta_o} Γe=2Recosθe+j(Re2+1)sinθej(Re2−1)sinθe,Γo=2Rocosθo+j(Ro2+1)sinθoj(Ro2−1)sinθo
要求 S 11 = 1 2 ( Γ e + Γ o ) = 0 S_{11} = \frac{1}{2}(\Gamma_e + \Gamma_o) = 0 S11=21(Γe+Γo)=0,即 Γ e + Γ o = 0 \Gamma_e + \Gamma_o = 0 Γe+Γo=0。通分
Γ e + Γ o = 2 j [ R o ( R e 2 − 1 ) sin θ e cos θ o + R e ( R o 2 − 1 ) sin θ o cos θ e ] − 2 ( R e 2 R o 2 − 1 ) sin θ e sin θ o [ 2 R e cos θ e + j ( R e 2 + 1 ) sin θ e ] [ 2 R o cos θ o + j ( R o 2 + 1 ) sin θ o ] \Gamma_e + \Gamma_o = \frac{2j \left[ R_o (R_e^2 - 1) \sin \theta_e \cos \theta_o + R_e (R_o^2 - 1) \sin \theta_o \cos \theta_e \right] - 2 (R_e^2 R_o^2 - 1) \sin \theta_e \sin \theta_o}{\left[ 2R_e \cos \theta_e + j(R_e^2 + 1) \sin \theta_e \right] \left[ 2R_o \cos \theta_o + j(R_o^2 + 1) \sin \theta_o \right]} Γe+Γo=[2Recosθe+j(Re2+1)sinθe][2Rocosθo+j(Ro2+1)sinθo]2j[Ro(Re2−1)sinθecosθo+Re(Ro2−1)sinθocosθe]−2(Re2Ro2−1)sinθesinθo
分子可以记为
N = A + j B N = A + jB N=A+jB
其中
A = − 2 ( R e 2 R o 2 − 1 ) sin θ e sin θ o , B = 2 [ R o ( R e 2 − 1 ) sin θ e cos θ o + R e ( R o 2 − 1 ) sin θ o cos θ e ] . A = -2 (R_e^2 R_o^2 - 1) \sin \theta_e \sin \theta_o, \quad B = 2 \left[ R_o (R_e^2 - 1) \sin \theta_e \cos \theta_o + R_e (R_o^2 - 1) \sin \theta_o \cos \theta_e \right]. A=−2(Re2Ro2−1)sinθesinθo,B=2[Ro(Re2−1)sinθecosθo+Re(Ro2−1)sinθocosθe].
由复数为零需要实部虚部分别为零
A=0:
sin θ e sin θ o ( R e 2 R o 2 − 1 ) = 0 \sin \theta_e \sin \theta_o (R_e^2 R_o^2 - 1) = 0 sinθesinθo(Re2Ro2−1)=0
在非平凡情况下( sin θ e ≠ 0 \sin \theta_e \neq 0 sinθe=0且 sin θ o ≠ 0 \sin \theta_o \neq 0 sinθo=0),需满足:
R e R o = 1 ⇒ Z 0 = Z 0 e Z 0 o R_e R_o = 1 \quad \Rightarrow \quad Z_0 = \sqrt{Z_{0e} Z_{0o}} ReRo=1⇒Z0=Z0eZ0o
B=0 (在满足 Z 0 = Z 0 e Z 0 o Z_0 = \sqrt{Z_{0e} Z_{0o}} Z0=Z0eZ0o 后):
B = 2 [ R o ( R e 2 − 1 ) sin θ e cos θ o + R e ( R o 2 − 1 ) sin θ o cos θ e ] B = 2 \left[ R_o (R_e^2 - 1) \sin \theta_e \cos \theta_o + R_e (R_o^2 - 1) \sin \theta_o \cos \theta_e \right] B=2[Ro(Re2−1)sinθecosθo+Re(Ro2−1)sinθocosθe]
R o ( R e 2 − 1 ) = R e 2 − 1 R e R_o (R_e^2 - 1) = \frac{R_e^2 - 1}{R_e} Ro(Re2−1)=ReRe2−1
R e ( R o 2 − 1 ) = R e ⋅ 1 − R e 2 R e 2 = 1 − R e 2 R e = − R e 2 − 1 R e R_e (R_o^2 - 1) = R_e \cdot \frac{1 - R_e^2}{R_e^2} = \frac{1 - R_e^2}{R_e} = -\frac{R_e^2 - 1}{R_e} Re(Ro2−1)=Re⋅Re21−Re2=Re1−Re2=−ReRe2−1
代入 B:
B = 2 [ R e 2 − 1 R e sin θ e cos θ o − R e 2 − 1 R e sin θ o cos θ e ] = 2 ⋅ R e 2 − 1 R e ( sin θ e cos θ o − sin θ o cos θ e ) \begin{aligned} B &= 2 \left[ \frac{R_e^2 - 1}{R_e} \sin \theta_e \cos \theta_o - \frac{R_e^2 - 1}{R_e} \sin \theta_o \cos \theta_e \right] \\ &= 2 \cdot \frac{R_e^2 - 1}{R_e} \left( \sin \theta_e \cos \theta_o - \sin \theta_o \cos \theta_e \right) \end{aligned} B=2[ReRe2−1sinθecosθo−ReRe2−1sinθocosθe]=2⋅ReRe2−1(sinθecosθo−sinθocosθe)
利用三角恒等式
sin θ e cos θ o − sin θ o cos θ e = sin ( θ e − θ o ) \sin \theta_e \cos \theta_o - \sin \theta_o \cos \theta_e = \sin(\theta_e - \theta_o) sinθecosθo−sinθocosθe=sin(θe−θo)
因此
B = 2 ⋅ R e 2 − 1 R e sin ( θ e − θ o ) = 0 B = 2 \cdot \frac{R_e^2 - 1}{R_e} \sin(\theta_e - \theta_o)=0 B=2⋅ReRe2−1sin(θe−θo)=0
当耦合非零时( Z 0 e ≠ Z 0 Z_{0e} \neq Z_0 Z0e=Z0),有 R e ≠ 1 R_e \neq 1 Re=1,所以 R e 2 − 1 R e ≠ 0 \dfrac{R_e^2 - 1}{R_e} \neq 0 ReRe2−1=0。因此必须满足:
sin ( θ e − θ o ) = 0 \sin(\theta_e - \theta_o) = 0 sin(θe−θo)=0
即
θ e − θ o = n π , n ∈ Z \theta_e - \theta_o = n\pi, \quad n \in \mathbb{Z} θe−θo=nπ,n∈Z
或写作
θ e = θ o + n π \theta_e = \theta_o + n\pi θe=θo+nπ
通常耦合微带线,电长度 θ e \theta_e θe和 θ o \theta_o θo小于 π \pi π(物理长度小于半个波长 ),且均为正数。因此要使上述等式成立取 n = 0 n = 0 n=0,得到:
θ e = θ o \theta_e = \theta_o θe=θo
2 R e 2 − 1 R e sin ( θ e − θ o ) = 0 2 \frac{R_e^2 - 1}{R_e} \sin(\theta_e - \theta_o) = 0 2ReRe2−1sin(θe−θo)=0
若 R e ≠ 1 R_e \neq 1 Re=1(即 Z 0 e ≠ Z 0 Z_{0e} \neq Z_0 Z0e=Z0,耦合非零),则需:
sin ( θ e − θ o ) = 0 ⇒ θ e = θ o + n π \sin(\theta_e - \theta_o) = 0 \quad \Rightarrow \quad \theta_e = \theta_o + n\pi sin(θe−θo)=0⇒θe=θo+nπ
对于通常的耦合线长度(电长度小于半波长),取 n = 0 n=0 n=0,即 θ e = θ o \theta_e = \theta_o θe=θo。
3、隔离条件( S 41 = 0 S_{41}=0 S41=0)
对于对称耦合微带线,端口4到端口1的隔离度 S 41 S_{41} S41 由散射矩阵给出:
S 41 = 1 2 ( T e − T o ) S_{41} = \frac{1}{2}(T_e - T_o) S41=21(Te−To)
因此, S 41 = 0 S_{41} = 0 S41=0的条件为 T e = T o T_e = T_o Te=To。代入 T e T_e Te 和 T o T_o To 的表达式并取倒数,得到:
2 cos θ e + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin θ e = 2 cos θ o + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin θ o 2 \cos \theta_e + j\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right) \sin \theta_e = 2 \cos \theta_o + j\left(\frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}}\right) \sin \theta_o 2cosθe+j(Z0Z0e+Z0eZ0)sinθe=2cosθo+j(Z0Z0o+Z0oZ0)sinθo
令实部和虚部分别相等:
cos θ e = cos θ o 和 ( Z 0 e Z 0 + Z 0 Z 0 e ) sin θ e = ( Z 0 o Z 0 + Z 0 Z 0 o ) sin θ o \cos \theta_e = \cos \theta_o \quad \text{和} \quad \left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right) \sin \theta_e = \left(\frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}}\right) \sin \theta_o cosθe=cosθo和(Z0Z0e+Z0eZ0)sinθe=(Z0Z0o+Z0oZ0)sinθo
由 cos θ e = cos θ o \cos \theta_e = \cos \theta_o cosθe=cosθo,在电长度通常小于 π \pi π 且为正的情况下,得到:
θ e = θ o \theta_e = \theta_o θe=θo
即偶模与奇模电长度相等,对应相速度相等 v p e = v p o v_{pe} = v_{po} vpe=vpo。
将 θ e = θ o = θ \theta_e = \theta_o = \theta θe=θo=θ 代入虚部方程,若 sin θ ≠ 0 \sin \theta \neq 0 sinθ=0,可约去 sin θ \sin \theta sinθ:
Z 0 e Z 0 + Z 0 Z 0 e = Z 0 o Z 0 + Z 0 Z 0 o \frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}} = \frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}} Z0Z0e+Z0eZ0=Z0Z0o+Z0oZ0
整理得:
Z 0 e + Z 0 2 Z 0 e = Z 0 o + Z 0 2 Z 0 o Z_{0e} + \frac{Z_0^2}{Z_{0e}} = Z_{0o} + \frac{Z_0^2}{Z_{0o}} Z0e+Z0eZ02=Z0o+Z0oZ02
假设 Z 0 e ≠ Z 0 o Z_{0e} \neq Z_{0o} Z0e=Z0o(耦合非零),化简后得到:
Z 0 = Z 0 e Z 0 o Z_0 = \sqrt{Z_{0e} Z_{0o}} Z0=Z0eZ0o
因此,当奇偶模相速度相等且奇偶模阻抗和参考阻抗满足几何平均值关系时,对称耦合微带线可实现理想匹配和隔离条件。
**若相速不相等( θ e ≠ θ o \theta_e \neq \theta_o θe=θo),即使满足阻抗条件,反射系数也无法完全抵消,导致端口失配( S 11 ≠ 0 S_{11} \neq 0 S11=0)。类似地,隔离度 S 41 = 0 S_{41}=0 S41=0的条件也会被破坏。**需通过结构优化(如介质覆盖、多节耦合线)等方法去补偿奇偶模相速度不同的影响,实现较为理想的匹配和隔离。
4、满足匹配&隔离条件情况下的简化耦合线S参数矩阵
S p = 1 2 [ Γ e + Γ o Γ e − Γ o T e + T o T e − T o Γ e − Γ o Γ e + Γ o T e − T o T e + T o T e + T o T e − T o Γ e + Γ o Γ e − Γ o T e − T o T e + T o Γ e − Γ o Γ e + Γ o ] \mathbf{S}_p = \frac{1}{2} \begin{bmatrix} \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o & T_e + T_o & T_e - T_o \\ \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o & T_e - T_o & T_e + T_o \\ T_e + T_o & T_e - T_o & \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o \\ T_e - T_o & T_e + T_o & \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o \end{bmatrix} Sp=21 Γe+ΓoΓe−ΓoTe+ToTe−ToΓe−ΓoΓe+ΓoTe−ToTe+ToTe+ToTe−ToΓe+ΓoΓe−ΓoTe−ToTe+ToΓe−ΓoΓe+Γo
容易根据匹配和隔离条件与对称性,得到主对角线和次对角线元素均为零 :
S p = 1 2 [ 0 Γ e − Γ o T e + T o 0 Γ e − Γ o 0 0 T e + T o T e + T o 0 0 Γ e − Γ o 0 T e + T o Γ e − Γ o 0 ] \mathbf{S}_p = \frac{1}{2} \begin{bmatrix} 0& \Gamma_e - \Gamma_o & T_e + T_o & 0 \\ \Gamma_e - \Gamma_o & 0 & 0 & T_e + T_o \\ T_e + T_o & 0 & 0 & \Gamma_e - \Gamma_o \\ 0 & T_e + T_o & \Gamma_e - \Gamma_o &0 \end{bmatrix} Sp=21 0Γe−ΓoTe+To0Γe−Γo00Te+ToTe+To00Γe−Γo0Te+ToΓe−Γo0
根据匹配条件有 θ e = θ o = θ = β l \theta_e=\theta_o=\theta=\beta l θe=θo=θ=βl,下面计算S21:
S 21 = Γ e − Γ o 2 = 1 2 [ j ( Z 0 e Z 0 − Z 0 Z 0 e ) sin β l 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l − j ( Z 0 o Z 0 − Z 0 Z 0 o ) sin β l 2 cos β l + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin β l ] = j sin β l 2 { ( Z 0 e Z 0 − Z 0 Z 0 e ) ( 2 cos β l + j ( Z 0 o Z 0 + Z 0 Z 0 o ) sin β l ) − ( Z 0 o Z 0 − Z 0 Z 0 o ) ( 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l ) } [ 2 cos β l + j sin β l ( Z 0 o Z 0 e + Z 0 e Z 0 o ) ] 2 = j sin β l 2 { 2 cos β l ( Z 0 e Z 0 − Z 0 Z 0 e − Z 0 o Z 0 + Z 0 Z 0 o ) + j sin β l [ ( Z 0 e Z 0 − Z 0 Z 0 e ) ( Z 0 o Z 0 + Z 0 Z 0 o ) − ( Z 0 o Z 0 − Z 0 Z 0 o ) ( Z 0 e Z 0 + Z 0 Z 0 e ) ] } [ 2 cos β l + j sin β l ( Z 0 o Z 0 e + Z 0 e Z 0 o ) ] 2 = j sin β l 2 { 4 cos β l Z 0 e − Z 0 o Z 0 + j 2 sin β l [ ( Z 0 e + Z 0 o ) ( Z 0 e − Z 0 o ) Z 0 2 ] } [ 2 cos β l + j sin β l ( Z 0 o Z 0 e + Z 0 e Z 0 o ) ] 2 = j sin β l 2 Z 0 e − Z 0 o Z 0 { 2 cos β l + j sin β l Z 0 e + Z 0 o Z 0 } [ 2 cos β l + j sin β l ( Z 0 o Z 0 e + Z 0 e Z 0 o ) ] 2 = j sin β l 2 Z 0 e − Z 0 o Z 0 { 2 cos β l + j sin β l Z 0 o + Z 0 e Z 0 } ( 2 cos β l + j sin β l Z 0 o + Z 0 e Z 0 ) 2 = j sin β l Z 0 e − Z 0 o Z 0 2 cos β l + j sin β l Z 0 e + Z 0 o Z 0 = j sin β l Z 0 e − Z 0 o Z 0 e + Z 0 o j sin β l + 2 Z 0 Z 0 e + Z 0 o cos β l \begin{align*} S_{21} & = \frac{\Gamma_{e} -\Gamma_{o}}{2} \\ & = \frac{1}{2} \left[ \frac{j\left( \frac{Z_{0e}}{Z_0} - \frac{Z_0}{Z_{0e}} \right) \sin \beta l}{2 \cos \beta l + j\left( \frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}} \right) \sin \beta l} - \frac{j\left( \frac{Z_{0o}}{Z_0} - \frac{Z_0}{Z_{0o}} \right) \sin \beta l}{2 \cos \beta l + j\left( \frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}} \right) \sin \beta l} \right] \\ & = \frac{ \frac{j \sin \beta l}{2} \left\{ \left( \frac{Z_{0e}}{Z_0} - \frac{Z_0}{Z_{0e}} \right) \left( 2 \cos \beta l + j\left( \frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}} \right) \sin \beta l \right) - \left( \frac{Z_{0o}}{Z_0} - \frac{Z_0}{Z_{0o}} \right) \left( 2 \cos \beta l + j\left( \frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}} \right) \sin \beta l \right) \right\} }{ \left[ 2 \cos \beta l + j \sin \beta l \left( \sqrt{ \frac{Z_{0o}}{Z_{0e}} } + \sqrt{ \frac{Z_{0e}}{Z_{0o}} } \right) \right]^2 } \\ & = \frac{ \frac{j \sin \beta l}{2} \left\{ 2 \cos \beta l \left( \frac{Z_{0e}}{Z_0} - \frac{Z_0}{Z_{0e}} - \frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}} \right) + j \sin \beta l \left[ \left( \frac{Z_{0e}}{Z_0} - \frac{Z_0}{Z_{0e}} \right) \left( \frac{Z_{0o}}{Z_0} + \frac{Z_0}{Z_{0o}} \right) - \left( \frac{Z_{0o}}{Z_0} - \frac{Z_0}{Z_{0o}} \right) \left( \frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}} \right) \right] \right\} }{ \left[ 2 \cos \beta l + j \sin \beta l \left( \sqrt{ \frac{Z_{0o}}{Z_{0e}} } + \sqrt{ \frac{Z_{0e}}{Z_{0o}} } \right) \right]^2 } \\ & = \frac{ \frac{j \sin \beta l}{2} \left\{ 4 \cos \beta l \frac{Z_{0e} - Z_{0o}}{Z_0} + j 2 \sin \beta l \left[ \frac{ (Z_{0e} + Z_{0o}) (Z_{0e} - Z_{0o}) }{Z_0^2} \right] \right\} }{ \left[ 2 \cos \beta l + j \sin \beta l \left( \sqrt{ \frac{Z_{0o}}{Z_{0e}} } + \sqrt{ \frac{Z_{0e}}{Z_{0o}} } \right) \right]^2 } \\ & = \frac{ \frac{j \sin \beta l}{2} \frac{Z_{0e} - Z_{0o}}{Z_0} \left\{ 2 \cos \beta l + j \sin \beta l \frac{Z_{0e} + Z_{0o}}{Z_0} \right\} }{ \left[ 2 \cos \beta l + j \sin \beta l \left( \sqrt{ \frac{Z_{0o}}{Z_{0e}} } + \sqrt{ \frac{Z_{0e}}{Z_{0o}} } \right) \right]^2 } \\ & = \frac{ \frac{j \sin \beta l}{2} \frac{Z_{0e} - Z_{0o}}{Z_0} \left\{ 2 \cos \beta l + j \sin \beta l \frac{Z_{0o} + Z_{0e}}{Z_0} \right\} }{ \left( 2 \cos \beta l + j \sin \beta l \frac{Z_{0o} + Z_{0e}}{Z_0} \right)^2 } \\ & = \frac{ j \sin \beta l \frac{Z_{0e} - Z_{0o}}{Z_0} }{ 2 \cos \beta l + j \sin \beta l \frac{Z_{0e} + Z_{0o}}{Z_0} } = \frac{ j \sin \beta l \frac{Z_{0e} - Z_{0o}}{Z_{0e}+ Z_{0o}} }{ j \sin \beta l + \frac{2 Z_0}{Z_{0e} + Z_{0o}} \cos \beta l } \end{align*} S21=2Γe−Γo=21 2cosβl+j(Z0Z0e+Z0eZ0)sinβlj(Z0Z0e−Z0eZ0)sinβl−2cosβl+j(Z0Z0o+Z0oZ0)sinβlj(Z0Z0o−Z0oZ0)sinβl =[2cosβl+jsinβl(Z0eZ0o +Z0oZ0e )]22jsinβl{(Z0Z0e−Z0eZ0)(2cosβl+j(Z0Z0o+Z0oZ0)sinβl)−(Z0Z0o−Z0oZ0)(2cosβl+j(Z0Z0e+Z0eZ0)sinβl)}=[2cosβl+jsinβl(Z0eZ0o +Z0oZ0e )]22jsinβl{2cosβl(Z0Z0e−Z0eZ0−Z0Z0o+Z0oZ0)+jsinβl[(Z0Z0e−Z0eZ0)(Z0Z0o+Z0oZ0)−(Z0Z0o−Z0oZ0)(Z0Z0e+Z0eZ0)]}=[2cosβl+jsinβl(Z0eZ0o +Z0oZ0e )]22jsinβl{4cosβlZ0Z0e−Z0o+j2sinβl[Z02(Z0e+Z0o)(Z0e−Z0o)]}=[2cosβl+jsinβl(Z0eZ0o +Z0oZ0e )]22jsinβlZ0Z0e−Z0o{2cosβl+jsinβlZ0Z0e+Z0o}=(2cosβl+jsinβlZ0Z0o+Z0e)22jsinβlZ0Z0e−Z0o{2cosβl+jsinβlZ0Z0o+Z0e}=2cosβl+jsinβlZ0Z0e+Z0ojsinβlZ0Z0e−Z0o=jsinβl+Z0e+Z0o2Z0cosβljsinβlZ0e+Z0oZ0e−Z0o
定义耦合系数 k k k
k = Z 0 e − Z 0 o Z 0 e + Z 0 o k=\frac{Z_{0e} - Z_{0o}}{Z_{0e} + Z_{0o}} k=Z0e+Z0oZ0e−Z0o
根据 Z 0 = Z 0 e Z 0 o Z_0 = \sqrt{Z_{0e} Z_{0o}} Z0=Z0eZ0o
1 − k 2 = 4 Z 0 e Z 0 o ( Z 0 e + Z 0 o ) 2 = 2 Z 0 e Z 0 o Z 0 e + Z 0 o = 2 Z 0 Z 0 e + Z 0 o \sqrt{1 - k^2}=\sqrt{ \frac{4Z_{0e}Z_{0o}}{(Z_{0e} + Z_{0o})^2}} = \frac{2\sqrt{Z_{0e}Z_{0o}}}{Z_{0e} + Z_{0o}} = \frac{2Z_0}{Z_{0e} + Z_{0o}} 1−k2 =(Z0e+Z0o)24Z0eZ0o =Z0e+Z0o2Z0eZ0o =Z0e+Z0o2Z0
把k带入 S 21 S_{21} S21表达式可得
S 21 = j k sin β l j sin β l + cos β l 1 − k 2 S_{21}= \frac{ j k \sin\beta l }{ j \sin \beta l +\cos \beta l \sqrt{1 - k^2} } S21=jsinβl+cosβl1−k2 jksinβl
观察S参数矩阵或者利用对称性易得 S 21 = S 12 = S 43 = S 34 S_{21}=S_{12}=S_{43}=S_{34} S21=S12=S43=S34
同理对于直通端口我们有
S 31 = T e + T o 2 = 1 2 cos β l + j ( Z 00 Z 0 + Z 0 Z 00 ) sin β l + 1 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l = 2 cos β l + j ( Z 00 Z 0 + Z 0 Z 00 ) sin β l + 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l [ 2 cos β l + j ( Z 00 Z 0 + Z 0 Z 00 ) sin β l ] × [ 2 cos β l + j ( Z 0 e Z 0 + Z 0 Z 0 e ) sin β l ] = 2 × [ 2 cos β l + j sin β l ( Z 00 Z 0 e + Z 0 e Z 00 ) ] 4 cos 2 β l + 4 j cos β l sin β l ( Z 00 Z 0 e + Z 00 Z 0 e ) − ( Z 00 Z 0 + Z 0 Z 00 ) ( Z 0 e Z 0 + Z 0 Z 0 e ) sin 2 β l = 2 × [ 2 cos β l + j sin β l ( Z 00 Z 0 e + Z 0 e Z 00 ) ] 4 cos 2 β l + 4 j cos β l sin β l ( Z 00 Z 0 e + Z 00 Z 0 e ) − ( 2 + Z 00 Z 0 e + Z 0 e Z 00 ) sin 2 β l = 2 × [ 2 cos β l + j sin β l ( Z 00 Z 0 e + Z 0 e Z 00 ) ] [ 2 cos β l + j sin β l ( Z 00 Z 0 e + Z 0 e Z 00 ) ] 2 = 2 2 cos β l + j sin β l ( Z 00 Z 0 e + Z 0 e Z 00 ) = 2 2 cos β l + j sin β l ⋅ Z 0 e + Z 00 Z 0 = 1 cos β l + j sin β l ⋅ 1 1 − k 2 \begin{align*} S_{31} &= \frac{T_{e} + T_{o}}{2} \\ &= \frac{1}{2\cos\beta l + j\left(\frac{Z_{00}}{Z_0} + \frac{Z_0}{Z_{00}}\right)\sin\beta l} + \frac{1}{2\cos\beta l + j\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right)\sin\beta l} \\ &= \frac{2\cos\beta l + j\left(\frac{Z_{00}}{Z_0} + \frac{Z_0}{Z_{00}}\right)\sin\beta l + 2\cos\beta l + j\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right)\sin\beta l}{\left[2\cos\beta l + j\left(\frac{Z_{00}}{Z_0} + \frac{Z_0}{Z_{00}}\right)\sin\beta l\right] \times \left[2\cos\beta l + j\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right)\sin\beta l\right]} \\ &= \frac{2 \times \left[2\cos\beta l + j\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{0e}}{Z_{00}}}\right)\right]}{4\cos^2\beta l + 4j\cos\beta l\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{00}}{Z_{0e}}}\right) - \left(\frac{Z_{00}}{Z_0} + \frac{Z_0}{Z_{00}}\right)\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right)\sin^2\beta l} \\ &= \frac{2 \times \left[2\cos\beta l + j\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{0e}}{Z_{00}}}\right)\right]}{4\cos^2\beta l + 4j\cos\beta l\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{00}}{Z_{0e}}}\right) - \left(2 + \frac{Z_{00}}{Z_{0e}} + \frac{Z_{0e}}{Z_{00}}\right)\sin^2\beta l} \\ &= \frac{2 \times \left[2\cos\beta l + j\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{0e}}{Z_{00}}}\right)\right]}{\left[2\cos\beta l + j\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{0e}}{Z_{00}}}\right)\right]^2} \\ &= \frac{2}{2\cos\beta l + j\sin\beta l\left(\sqrt{\frac{Z_{00}}{Z_{0e}}} + \sqrt{\frac{Z_{0e}}{Z_{00}}}\right)} \\ &= \frac{2}{2\cos\beta l + j\sin\beta l \cdot \frac{Z_{0e} + Z_{00}}{Z_0}}=\frac{1}{\cos\beta l + j\sin\beta l \cdot \dfrac{1}{\sqrt{1 - k^2}}} \end{align*} S31=2Te+To=2cosβl+j(Z0Z00+Z00Z0)sinβl1+2cosβl+j(Z0Z0e+Z0eZ0)sinβl1=[2cosβl+j(Z0Z00+Z00Z0)sinβl]×[2cosβl+j(Z0Z0e+Z0eZ0)sinβl]2cosβl+j(Z0Z00+Z00Z0)sinβl+2cosβl+j(Z0Z0e+Z0eZ0)sinβl=4cos2βl+4jcosβlsinβl(Z0eZ00 +Z0eZ00 )−(Z0Z00+Z00Z0)(Z0Z0e+Z0eZ0)sin2βl2×[2cosβl+jsinβl(Z0eZ00 +Z00Z0e )]=4cos2βl+4jcosβlsinβl(Z0eZ00 +Z0eZ00 )−(2+Z0eZ00+Z00Z0e)sin2βl2×[2cosβl+jsinβl(Z0eZ00 +Z00Z0e )]=[2cosβl+jsinβl(Z0eZ00 +Z00Z0e )]22×[2cosβl+jsinβl(Z0eZ00 +Z00Z0e )]=2cosβl+jsinβl(Z0eZ00 +Z00Z0e )2=2cosβl+jsinβl⋅Z0Z0e+Z002=cosβl+jsinβl⋅1−k2 11
即
S 31 = 1 − k 2 cos β l 1 − k 2 + j sin β l ⋅ S_{31}=\frac{\sqrt{1 - k^2}}{\cos\beta l\sqrt{1 - k^2} + j\sin\beta l \cdot } S31=cosβl1−k2 +jsinβl⋅1−k2
观察S参数矩阵或者利用对称性易得 S 31 = S 42 = S 24 = S 13 S_{31}=S_{42}=S_{24}=S_{13} S31=S42=S24=S13
S p = [ 0 j k sin β l j sin β l + cos β l 1 − k 2 1 − k 2 cos β l 1 − k 2 + j sin β l ⋅ 0 j k sin β l j sin β l + cos β l 1 − k 2 0 0 1 − k 2 cos β l 1 − k 2 + j sin β l ⋅ 1 − k 2 cos β l 1 − k 2 + j sin β l ⋅ 0 0 j k sin β l j sin β l + cos β l 1 − k 2 0 1 − k 2 cos β l 1 − k 2 + j sin β l ⋅ j k sin β l j sin β l + cos β l 1 − k 2 0 ] \mathbf{S}_p = \begin{bmatrix} 0& \frac{ j k \sin\beta l }{ j \sin \beta l +\cos \beta l \sqrt{1 - k^2} } & \frac{\sqrt{1 - k^2}}{\cos\beta l\sqrt{1 - k^2} + j\sin\beta l \cdot } & 0 \\ \frac{ j k \sin\beta l }{ j \sin \beta l +\cos \beta l \sqrt{1 - k^2} } & 0 & 0 &\frac{\sqrt{1 - k^2}}{\cos\beta l\sqrt{1 - k^2} + j\sin\beta l \cdot } \\ \frac{\sqrt{1 - k^2}}{\cos\beta l\sqrt{1 - k^2} + j\sin\beta l \cdot } & 0 & 0 & \frac{ j k \sin\beta l }{ j \sin \beta l +\cos \beta l \sqrt{1 - k^2} } \\ 0 & \frac{\sqrt{1 - k^2}}{\cos\beta l\sqrt{1 - k^2} + j\sin\beta l \cdot }& \frac{ j k \sin\beta l }{ j \sin \beta l +\cos \beta l \sqrt{1 - k^2} } &0 \end{bmatrix} Sp= 0jsinβl+cosβl1−k2 jksinβlcosβl1−k2 +jsinβl⋅1−k2 0jsinβl+cosβl1−k2 jksinβl00cosβl1−k2 +jsinβl⋅1−k2 cosβl1−k2 +jsinβl⋅1−k2 00jsinβl+cosβl1−k2 jksinβl0cosβl1−k2 +jsinβl⋅1−k2 jsinβl+cosβl1−k2 jksinβl0
当 θ = 2 π l / λ = β l = 1 / 4 π \theta=2\pi l/\lambda=\beta l=1/4\pi θ=2πl/λ=βl=1/4π时,对应四分之波长传输线
S p = [ 0 k − j 1 − k 2 0 k 0 0 − j 1 − k 2 − j 1 − k 2 0 0 k 0 − j 1 − k 2 C 0 ] \mathbf{S}_p = \begin{bmatrix} 0& k &-j\sqrt{1 - k^2} & 0 \\ k & 0 & 0 &-j\sqrt{1 - k^2} \\ -j\sqrt{1 - k^2}& 0 & 0 & k \\ 0 & -j\sqrt{1 - k^2}& C &0 \end{bmatrix} Sp= 0k−j1−k2 0k00−j1−k2 −j1−k2 00C0−j1−k2 k0
可以看到交换2,3端口定义与图2表达式相同

图2:RF and Microwave Coupled-Line Circuits推导的结果