前要回顾
设四端口网络的端口电压和电流(定义所有电流流入网络为正)为:
Vp=[U1,U2,U3,U4]T,Ip=[I1,I2,I3,I4]T. \mathbf{V}_p = [U_1, U_2, U_3, U_4]^T, \quad \mathbf{I}_p = [I_1, I_2, I_3, I_4]^T. Vp=[U1,U2,U3,U4]T,Ip=[I1,I2,I3,I4]T.
四端口网络反射波和入射波定义为:
Bp=[b1,b2,b3,b4]T,Ap=[a1,a2,a3,a4]T.(1) \mathbf{B}p = [b_1, b_2, b_3, b_4]^T, \quad \mathbf{A}p = [a_1, a_2, a_3,a_4]^T.\quad(1) Bp=[b1,b2,b3,b4]T,Ap=[a1,a2,a3,a4]T.(1)
S11=ReflectedIncident=b1a1∣a2=0(输入端反射系数/输入匹配)S21=TransmittedIncident=b2a1∣a2=0(正向传输系数/增益或损耗)S22=ReflectedIncident=b2a2∣a1=0(输出端反射系数/输出匹配)S12=TransmittedIncident=b1a2∣a1=0(反向传输系数/隔离) \begin{aligned} S{11} &= \frac{\text{Reflected}}{\text{Incident}} = \left.\frac{b_1}{a_1}\right|{a_2=0} && \text{(输入端反射系数/输入匹配)} \\ S_{21} &= \frac{\text{Transmitted}}{\text{Incident}} = \left.\frac{b_2}{a_1}\right|{a_2=0} && \text{(正向传输系数/增益或损耗)} \\ S{22} &= \frac{\text{Reflected}}{\text{Incident}} = \left.\frac{b_2}{a_2}\right|{a_1=0} && \text{(输出端反射系数/输出匹配)} \\ S{12} &= \frac{\text{Transmitted}}{\text{Incident}} = \left.\frac{b_1}{a_2}\right|_{a_1=0} && \text{(反向传输系数/隔离)} \end{aligned} S11S21S22S12=IncidentReflected=a1b1 a2=0=IncidentTransmitted=a1b2 a2=0=IncidentReflected=a2b2 a1=0=IncidentTransmitted=a2b1 a1=0(输入端反射系数/输入匹配)(正向传输系数/增益或损耗)(输出端反射系数/输出匹配)(反向传输系数/隔离)
四端口S参数矩阵如下。
b1b2b3b4\]=\[S11S12S13S14S21S22S23S24S31S32S33S34S41S42S43S44\]\[a1a2a3a4\] \\begin{bmatrix} b_{1} \\\\ b_{2} \\\\ b_{3} \\\\ b_{4} \\end{bmatrix} =\\begin{bmatrix} S_{11} \& S_{12} \& S_{13} \& S_{14} \\\\ S_{21} \& S_{22} \& S_{23} \& S_{24} \\\\ S_{31} \& S_{32} \& S_{33} \& S_{34} \\\\ S_{41} \& S_{42} \& S_{43} \& S_{44} \\end{bmatrix} \\begin{bmatrix} a_{1} \\\\ a_{2} \\\\ a_{3} \\\\ a_{4} \\end{bmatrix} b1b2b3b4 = S11S21S31S41S12S22S32S42S13S23S33S43S14S24S34S44 a1a2a3a4 式中bib_ibi为反射波,aia_iai为入射波 奇偶模电压、电流定义为: Vm=\[UeI,UeII,UoI,UoII\]T,Im=\[IeI,IeII,IoI,IoII\]T. \\mathbf{V}_m = \[U_e\^I, U_e\^{II}, U_o\^I, U_o\^{II}\]\^T, \\quad \\mathbf{I}_m = \[I_e\^I, I_e\^{II}, I_o\^I, I_o\^{II}\]\^T. Vm=\[UeI,UeII,UoI,UoII\]T,Im=\[IeI,IeII,IoI,IoII\]T. 奇偶模入射波和反射波定义为: Bm=\[beI,beII,boI,boII\]T,Am=\[aeI,aeII,aoI,aoII\]T.(2) \\mathbf{B}_m = \[b_e\^I, b_e\^{II}, b_o\^{I},b_o\^{II}\]\^T, \\quad \\mathbf{A}_m = \[a_e\^I, a_e\^{II}, a_o\^{I},a_o\^{II}\]\^T.\\quad(2) Bm=\[beI,beII,boI,boII\]T,Am=\[aeI,aeII,aoI,aoII\]T.(2) **这里讨论的是如对称不均匀的耦合微带线,在图2中左右1和3端口、2和4端口满足对称条件** 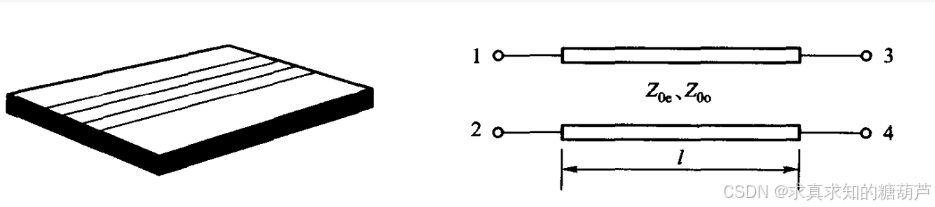 图1 端口顺序定义,推导S参数矩阵时每个端口端接对地特性阻抗Z0 参考前面的6篇文章中我们推出了如下公式 \[U1U2\]=\[111−1\]\[UeIUoI\](3) \\left\[\\begin{array}{l} U_{1} \\\\ U_{2} \\end{array}\\right\]=\\left\[\\begin{array}{cc} 1 \& 1 \\\\ 1 \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} U_{\\mathrm{e}}\^{I} \\\\ U_{\\mathrm{o}}\^{I} \\end{array}\\right\] \\quad(3) \[U1U2\]=\[111−1\]\[UeIUoI\](3) \[U3U4\]=\[111−1\]\[UeIIUoII\](4) \\left\[\\begin{array}{l} U_{3} \\\\ U_{4} \\end{array}\\right\]=\\left\[\\begin{array}{cc} 1 \& 1 \\\\ 1 \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} U_{\\mathrm{e}}\^{II} \\\\ U_{\\mathrm{o}}\^{II} \\end{array}\\right\] \\quad(4) \[U3U4\]=\[111−1\]\[UeIIUoII\](4) \[IeIIoI\]=12\[111−1\]\[I1I2\](5) \\left\[\\begin{array}{l} I_{\\mathrm{e}}\^{I} \\\\ I_{\\mathrm{o}}\^{I} \\end{array}\\right\]=\\frac{1}{2}\\left\[\\begin{array}{cc} 1 \& 1 \\\\ 1 \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} I_{1} \\\\ I_{2} \\end{array}\\right\] \\quad(5) \[IeIIoI\]=21\[111−1\]\[I1I2\](5) \[IeIIIoII\]=12\[111−1\]\[I3I4\](6) \\left\[\\begin{array}{l} I_{\\mathrm{e}}\^{II} \\\\ I_{\\mathrm{o}}\^{II} \\end{array}\\right\]=\\frac{1}{2}\\left\[\\begin{array}{cc} 1 \& 1 \\\\ 1 \& -1 \\end{array}\\right\]\\left\[\\begin{array}{l} I_{3} \\\\ I_{4} \\end{array}\\right\] \\quad(6) \[IeIIIoII\]=21\[111−1\]\[I3I4\](6) 传输线ABCD矩阵可以由如下二式表示 \[Ue1Ie1\]=\[cosθejZ0esinθejY0esinθecosθe\]\[UeIIIeII\](7) \\begin{bmatrix} U_e\^1 \\\\ I_e\^1 \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_e \& j Z_{0e} \\sin \\theta_e \\\\ j Y_{0e} \\sin \\theta_e \& \\cos \\theta_e \\end{bmatrix} \\begin{bmatrix} U_e\^{II} \\\\ I_e\^{II} \\end{bmatrix}\\qquad(7) \[Ue1Ie1\]=\[cosθejY0esinθejZ0esinθecosθe\]\[UeIIIeII\](7) \[Uo1Io1\]=\[cosθojZ0osinθojY0osinθocosθo\]\[UoIIIoII\](8) \\begin{bmatrix} U_o\^1 \\\\ I_o\^1 \\end{bmatrix} = \\begin{bmatrix} \\cos \\theta_o \& j Z_{0o} \\sin \\theta_o \\\\ j Y_{0o} \\sin \\theta_o \& \\cos \\theta_o \\end{bmatrix} \\begin{bmatrix} U_o\^{II} \\\\ I_o\^{II} \\end{bmatrix}\\qquad(8) \[Uo1Io1\]=\[cosθojY0osinθojZ0osinθocosθo\]\[UoIIIoII\](8) (这里 Y0e=1/Z0e,Y0o=1/Z0oY_{0e} = 1/Z_{0e}, Y_{0o} = 1/Z_{0o}Y0e=1/Z0e,Y0o=1/Z0o) 分析思路:采用类似上一节的方法,我们已经推出了耦合微带线的四端口A参数和Z参数与Y参数矩阵,下面我们需要将去耦后的传输线ABCD参数转换为二端口的S参数矩阵。 全过程如下通过**奇偶模分解法,**将四端口网络分解为偶模和奇模两个独立的传输线二端口网络,然后通过**前后两个转换矩阵,将端口波与奇偶模波联系起来**组合得到整体S参数。 #### 1. 端口奇偶模分解-变换矩阵 将四端口网络分解为偶模和奇模两个独立的二端口网络,其电压电流关系由给定公式(3)-(8)描述: \[U1U2\]=T\[UeIUoI\],\[U3U4\]=T\[UeIIUoII\],T=\[111−1\] \\begin{bmatrix} U_1 \\\\ U_2 \\end{bmatrix} = T \\begin{bmatrix} U_e\^I \\\\ U_o\^I \\end{bmatrix}, \\quad \\begin{bmatrix} U_3 \\\\ U_4 \\end{bmatrix} = T \\begin{bmatrix} U_e\^{II} \\\\ U_o\^{II} \\end{bmatrix}, \\quad T = \\begin{bmatrix} 1 \& 1 \\\\1 \& -1 \\end{bmatrix} \[U1U2\]=T\[UeIUoI\],\[U3U4\]=T\[UeIIUoII\],T=\[111−1
IeIIoI\]=TI\[I1I2\],\[IeIIIoII\]=TI\[I3I4\],TI=12\[111−1\] \\begin{bmatrix} I_e\^I \\\\ I_o\^I \\end{bmatrix} = T_I \\begin{bmatrix} I_1 \\\\ I_2 \\end{bmatrix}, \\quad \\begin{bmatrix} I_e\^{II} \\\\ I_o\^{II} \\end{bmatrix} = T_I \\begin{bmatrix} I_3 \\\\ I_4 \\end{bmatrix}, \\quad T_I = \\frac{1}{2} \\begin{bmatrix} 1 \& 1 \\\\ 1 \& -1 \\end{bmatrix} \[IeIIoI\]=TI\[I1I2\],\[IeIIIoII\]=TI\[I3I4\],TI=21\[111−1
根据奇偶模分解原理,端口电压、电流与奇偶模电压、电流的线性变换关系为:
U1U2\]=\[111−1\]\[UeIUoI\],\[I1I2\]=\[111−1\]\[IeIIoI\] \\begin{bmatrix} U_1 \\\\ U_2 \\end{bmatrix} = \\begin{bmatrix} 1 \& 1 \\\\ 1 \& -1 \\end{bmatrix} \\begin{bmatrix} U_e\^I \\\\ U_o\^I \\end{bmatrix}, \\quad \\begin{bmatrix} I_1 \\\\ I_2 \\end{bmatrix} = \\begin{bmatrix} 1 \& 1 \\\\ 1 \& -1 \\end{bmatrix} \\begin{bmatrix} I_e\^I \\\\ I_o\^I \\end{bmatrix} \[U1U2\]=\[111−1\]\[UeIUoI\],\[I1I2\]=\[111−1\]\[IeIIoI
在端口参考阻抗均为 Z0Z_0Z0 的前提下,定义端口入射波、反射波与奇偶模入射波、反射波(均相对于参考阻抗 Z0Z_0Z0归一化,方便导出一个简单的的变换矩阵关系,这样在奇偶模模态矩阵计算的时候也需要重新对参考阻抗Z0Z_0Z0归一化)为:
ai=12Z0(Ui+Z0Ii),bi=12Z0(Ui−Z0Ii) a_i = \frac{1}{2\sqrt{Z_0}}(U_i + Z_0 I_i), \quad b_i = \frac{1}{2\sqrt{Z_0}}(U_i - Z_0 I_i) ai=2Z0 1(Ui+Z0Ii),bi=2Z0 1(Ui−Z0Ii)
aeI=12Z0(UeI+Z0IeI),beI=12Z0(UeI−Z0IeI)aoI=12Z0(UoI+Z0IoI),boI=12Z0(UoI−Z0IoI)aeII=12Z0(UeII+Z0IeII),beII=12Z0(UeII−Z0IeII)aoII=12Z0(UoII+Z0IoII),boII=12Z0(UoII−Z0IoII) a_e^I = \frac{1}{2\sqrt{Z_0}}(U_e^I + Z_0 I_e^I), \quad b_e^I = \frac{1}{2\sqrt{Z_0}}(U_e^I - Z_0 I_e^I) \\ a_o^I = \frac{1}{2\sqrt{Z_0}}(U_o^I + Z_0 I_o^I), \quad b_o^I = \frac{1}{2\sqrt{Z_0}}(U_o^I - Z_0 I_o^I) \\ a_e^{II} = \frac{1}{2\sqrt{Z_0}}(U_e^{II} + Z_0 I_e^{II}), \quad b_e^{II} = \frac{1}{2\sqrt{Z_0}}(U_e^{II} - Z_0 I_e^{II}) \\ a_o^{II} = \frac{1}{2\sqrt{Z_0}}(U_o^{II} + Z_0 I_o^{II}), \quad b_o^{II} = \frac{1}{2\sqrt{Z_0}}(U_o^{II} - Z_0 I_o^{II}) aeI=2Z0 1(UeI+Z0IeI),beI=2Z0 1(UeI−Z0IeI)aoI=2Z0 1(UoI+Z0IoI),boI=2Z0 1(UoI−Z0IoI)aeII=2Z0 1(UeII+Z0IeII),beII=2Z0 1(UeII−Z0IeII)aoII=2Z0 1(UoII+Z0IoII),boII=2Z0 1(UoII−Z0IoII)
1.1 变换关系推导
由端口电压、电流与奇偶模电压、电流的线性关系,结合波定义式,得到:
a1=aeI+aoI,b1=beI+boI,a2=aeI−aoI,b2=beI−boI,a3=aeII+aoII,b3=beII+boII,a4=aeII−aoII,b4=beII−boII. \begin{aligned} a_1 &= a_e^I + a_o^I, \quad &b_1 = b_e^I + b_o^I, \\ a_2 &= a_e^I - a_o^I, \quad &b_2 = b_e^I - b_o^I, \\ a_3 &= a_e^{II} + a_o^{II}, \quad &b_3 = b_e^{II} + b_o^{II}, \\ a_4 &= a_e^{II} - a_o^{II}, \quad &b_4 = b_e^{II} - b_o^{II}. \end{aligned} a1a2a3a4=aeI+aoI,=aeI−aoI,=aeII+aoII,=aeII−aoII,b1=beI+boI,b2=beI−boI,b3=beII+boII,b4=beII−boII.
在前面的(1)(2)中我们定义了Ap=[a1,a2,a3,a4]T\mathbf{A}_p = [a_1, a_2, a_3, a_4]^TAp=[a1,a2,a3,a4]T,Bp=[b1,b2,b3,b4]T\mathbf{B}_p = [b_1, b_2, b_3, b_4]^TBp=[b1,b2,b3,b4]T为端口波;Am=[aeI,aeII,aoI,aoII]T\mathbf{A}_m = [a_e^I, a_e^{II}, a_o^I, a_o^{II}]^TAm=[aeI,aeII,aoI,aoII]T,Bm=[beI,beII,boI,boII]T\mathbf{B}_m = [b_e^I, b_e^{II}, b_o^I, b_o^{II}]^TBm=[beI,beII,boI,boII]T 为奇偶模波。下面推导变换矩阵。
1.2 变换矩阵
将上述关系写成矩阵形式:
(Am→Ap\mathbf{A}_m \to \mathbf{A}_pAm→Ap,Bm→Bp\mathbf{B}_m \to \mathbf{B}_pBm→Bp):
Ap\]=\[T\]\[Am\], \\begin{bmatrix} \\mathbf{A}_p \\\\ \\end{bmatrix} = \\begin{bmatrix} T \\end{bmatrix} \\begin{bmatrix} \\mathbf{A}_m \\end{bmatrix}, \[Ap\]=\[T\]\[Am\], \[Bp\]=\[T\]\[Bm\], \\begin{bmatrix} \\mathbf{B}_p \\end{bmatrix} = \\begin{bmatrix} T \\end{bmatrix} \\begin{bmatrix}\\mathbf{B}_m \\end{bmatrix}, \[Bp\]=\[T\]\[Bm\], 也可以写成 \[ApBp\]=\[T00T\]\[AmBm\], \\begin{bmatrix} \\mathbf{A}_p \\\\ \\mathbf{B}_p \\end{bmatrix} = \\begin{bmatrix} T \& 0 \\\\ 0 \& T \\end{bmatrix} \\begin{bmatrix} \\mathbf{A}_m \\\\ \\mathbf{B}_m \\end{bmatrix}, \[ApBp\]=\[T00T\]\[AmBm\], 其中 T=\[101010−100101010−1\]. T = \\begin{bmatrix} 1 \& 0 \& 1 \& 0 \\\\ 1 \& 0 \& -1 \& 0 \\\\ 0 \& 1 \& 0 \& 1 \\\\ 0 \& 1 \& 0 \& -1 \\end{bmatrix}. T= 110000111−100001−1 . **反过来也一样** (Ap→Am\\mathbf{A}_p \\to \\mathbf{A}_mAp→Am,Bp→Bm\\mathbf{B}_p \\to \\mathbf{B}_mBp→Bm): \[AmBm\]=\[T−100T−1\]\[ApBp\], \\begin{bmatrix} \\mathbf{A}_m \\\\ \\mathbf{B}_m \\end{bmatrix} = \\begin{bmatrix} T\^{-1} \& 0 \\\\ 0 \& T\^{-1} \\end{bmatrix} \\begin{bmatrix} \\mathbf{A}_p \\\\ \\mathbf{B}_p \\end{bmatrix}, \[AmBm\]=\[T−100T−1\]\[ApBp\], 其中 T−1=12\[110000111−100001−1\]. T\^{-1} = \\frac{1}{2} \\begin{bmatrix} 1 \& 1 \& 0 \& 0 \\\\ 0 \& 0 \& 1 \& 1 \\\\ 1 \& -1 \& 0 \& 0 \\\\ 0 \& 0 \& 1 \& -1 \\end{bmatrix}. T−1=21 101010−100101010−1 . > 矩阵 TTT 将模态入射波/反射波线性组合为端口入射波/反射波。逆矩阵T−1T\^{-1}T−1实现端口波到模态波的分解,用于奇偶模分析。接下来可以利用该变换和模态散射矩阵 Sm=diag(Se,So)\\mathbf{S}_m = \\operatorname{diag}(\\mathbf{S}\^e, \\mathbf{S}\^o)Sm=diag(Se,So),来得到整体散射矩阵Sp=TSmT−1\\mathbf{S}_p = T \\mathbf{S}_m T\^{-1}Sp=TSmT−1。 #### 2. S参数模态矩阵 偶模和奇模传输线的ABCD矩阵由公式(7)-(8)给出,将偶模和奇模二端口网络的ABCD参数转换为S参数(两个端口电流均定义为流入网络)**四个端口参考阻抗均为Z0Z_0Z0**: 对奇偶模传输线我们有如下方程: \[beIbeII\]=\[Se\]\[aeIaeII\] \\begin{bmatrix} b_e\^I \\\\ b_e\^{II} \\end{bmatrix} = \\begin{bmatrix} S\^e\\end{bmatrix} \\begin{bmatrix} a_e\^{I} \\\\ a_e\^{II} \\end{bmatrix} \[beIbeII\]=\[Se\]\[aeIaeII
boIboII\]=\[So\]\[aoIaoII\] \\begin{bmatrix} b_o\^I \\\\ b_o\^{II} \\end{bmatrix} = \\begin{bmatrix} S\^o\\end{bmatrix} \\begin{bmatrix} a_o\^{I} \\\\ a_o\^{II} \\end{bmatrix} \[boIboII\]=\[So\]\[aoIaoII
根据传输线A参数转换S参数公式奇偶模参考阻抗也为Z0Z_0Z0:
S=[S11S12S21S22]=[A+BZ0−CZ0−DA+BZ0+CZ0+D2(AD−BC)A+BZ0+CZ0+D2A+BZ0+CZ0+D−A+BZ0−CZ0+DA+BZ0+CZ0+D] \mathcal{S}=\left[\begin{array}{ll} S_{11} & S_{12} \\ S_{21} & S_{22} \end{array}\right]=\left[\begin{array}{ll} \displaystyle\frac{A+\frac{B}{Z_{0}}-C Z_{0}-D}{A+\frac{B}{Z_{0}}+C Z_{0}+D} & \displaystyle\frac{2(A D-B C)}{A+\frac{B}{Z_{0}}+C Z_{0}+D} \\[12pt] \displaystyle\frac{2}{A+\frac{B}{Z_{0}}+C Z_{0}+D} & \displaystyle\frac{-A+\frac{B}{Z_{0}}-C Z_{0}+D}{A+\frac{B}{Z_{0}}+C Z_{0}+D} \end{array}\right] S=[S11S21S12S22]= A+Z0B+CZ0+DA+Z0B−CZ0−DA+Z0B+CZ0+D2A+Z0B+CZ0+D2(AD−BC)A+Z0B+CZ0+D−A+Z0B−CZ0+D
可以分别得到模态去耦 后的奇偶模的单根传输线S参数模态矩阵
So=[j(Z00Z0−Z0Z00)sinθo2cosθo+j(Z00Z0+Z0Z00)sinθo22cosθo+j(Z00Z0+Z0Z00)sinθo22cosθo+j(Z00Z0+Z0Z00)sinθoj(Z00Z0−Z0Z00)sinθo2cosθo+j(Z00Z0+Z0Z00)sinθo] S^o=\left[\begin{array}{cc} \displaystyle\frac{j\left(\frac{Z_{00}}{Z_{0}}-\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o}{2 \cos \theta_o+j\left(\frac{Z_{00}}{Z_{0}}+\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o} & \displaystyle\frac{2}{2 \cos \theta_o+j\left(\frac{Z_{00}}{Z_{0}}+\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o} \\[12pt] \displaystyle\frac{2}{2 \cos \theta_o+j\left(\frac{Z_{00}}{Z_{0}}+\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o} & \displaystyle\frac{j\left(\frac{Z_{00}}{Z_{0}}-\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o}{2 \cos \theta_o+j\left(\frac{Z_{00}}{Z_{0}}+\frac{Z_{0}}{Z_{00}}\right) \sin \theta_o} \end{array}\right] So= 2cosθo+j(Z0Z00+Z00Z0)sinθoj(Z0Z00−Z00Z0)sinθo2cosθo+j(Z0Z00+Z00Z0)sinθo22cosθo+j(Z0Z00+Z00Z0)sinθo22cosθo+j(Z0Z00+Z00Z0)sinθoj(Z0Z00−Z00Z0)sinθo
Se=[j(Z0eZ0−Z0Z0e)sinθe2cosθe+j(Z0eZ0+Z0Z0e)sinθe22cosθe+j(Z0eZ0+Z0Z0e)sinθe22cosθe+j(Z0eZ0+Z0Z0e)sinθej(Z0eZ0−Z0Z0e)sinθe2cosθe+j(Z0eZ0+Z0Z0e)sinθe] S^e=\left[\begin{array}{cc} \displaystyle\frac{j\left(\frac{Z_{0 e}}{Z_{0}}-\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e}{2 \cos \theta_e+j\left(\frac{Z_{0 e}}{Z_{0}}+\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e} & \displaystyle\frac{2}{2 \cos \theta_e+j\left(\frac{Z_{0 e}}{Z_{0}}+\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e} \\[12pt] \displaystyle\frac{2}{2 \cos \theta_e+j\left(\frac{Z_{0 e}}{Z_{0}}+\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e} & \displaystyle\frac{j\left(\frac{Z_{0 e}}{Z_{0}}-\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e}{2 \cos \theta_e+j\left(\frac{Z_{0 e}}{Z_{0}}+\frac{Z_{0}}{Z_{0 e}}\right) \sin \theta_e} \end{array}\right] Se= 2cosθe+j(Z0Z0e+Z0eZ0)sinθej(Z0Z0e−Z0eZ0)sinθe2cosθe+j(Z0Z0e+Z0eZ0)sinθe22cosθe+j(Z0Z0e+Z0eZ0)sinθe22cosθe+j(Z0Z0e+Z0eZ0)sinθej(Z0Z0e−Z0eZ0)sinθe
Bm=[Sm]Am=[beI,beII,boI,boII]T=[Sm][aeI,aeII,aoI,aoII]T. \mathbf{B}_m =[S_m] \mathbf{A}_m= [b_e^I, b_e^{II}, b_o^{I},b_o^{II}]^T = [S_m][a_e^I, a_e^{II}, a_o^{I},a_o^{II}]^T. Bm=[Sm]Am=[beI,beII,boI,boII]T=[Sm][aeI,aeII,aoI,aoII]T.
合并得到四端口模态传输矩阵为
Sm=[Se00So] S_m = \begin{bmatrix} S^e & 0 \\ 0 & S^o \end{bmatrix} Sm=[Se00So]
对称耦合微带线四端口网络的整体 S 参数矩阵可通过奇偶模分解法推导,其中偶模和奇模二端口网络的 S 参数分别为:
Se=[ΓeTeTeΓe],So=[ΓoToToΓo] \mathbf{S}^e = \begin{bmatrix} \Gamma_e & T_e \\ T_e & \Gamma_e \end{bmatrix}, \quad \mathbf{S}^o = \begin{bmatrix} \Gamma_o & T_o \\ T_o & \Gamma_o \end{bmatrix} Se=[ΓeTeTeΓe],So=[ΓoToToΓo]
其中:
Γe=j(Z0eZ0−Z0Z0e)sinθe2cosθe+j(Z0eZ0+Z0Z0e)sinθe,Te=22cosθe+j(Z0eZ0+Z0Z0e)sinθe \Gamma_e = \frac{j\left(\frac{Z_{0e}}{Z_{0}}-\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e}{2 \cos \theta_e + j\left(\frac{Z_{0e}}{Z_{0}}+\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e}, \quad T_e = \frac{2}{2 \cos \theta_e + j\left(\frac{Z_{0e}}{Z_{0}}+\frac{Z_{0}}{Z_{0e}}\right) \sin \theta_e} Γe=2cosθe+j(Z0Z0e+Z0eZ0)sinθej(Z0Z0e−Z0eZ0)sinθe,Te=2cosθe+j(Z0Z0e+Z0eZ0)sinθe2
Γo=j(Z0oZ0−Z0Z0o)sinθo2cosθo+j(Z0oZ0+Z0Z0o)sinθo,To=22cosθo+j(Z0oZ0+Z0Z0o)sinθo \Gamma_o = \frac{j\left(\frac{Z_{0o}}{Z_{0}}-\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o}{2 \cos \theta_o + j\left(\frac{Z_{0o}}{Z_{0}}+\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o}, \quad T_o = \frac{2}{2 \cos \theta_o + j\left(\frac{Z_{0o}}{Z_{0}}+\frac{Z_{0}}{Z_{0o}}\right) \sin \theta_o} Γo=2cosθo+j(Z0Z0o+Z0oZ0)sinθoj(Z0Z0o−Z0oZ0)sinθo,To=2cosθo+j(Z0Z0o+Z0oZ0)sinθo2
Γe\Gamma_eΓeΓo\Gamma_oΓo 为偶奇模二端口网络的输入反射系数,定义为beI/aeIb_e^I / a_e^I\quadbeI/aeIboI/aoIb_o^I / a_o^IboI/aoI(输出端接匹配负载Z0Z_0Z0)。表达式分子正比于j(Z0eZ0−Z0Z0e)sinθej\left(\frac{Z_{0e}}{Z_0} - \frac{Z_0}{Z_{0e}}\right) \sin\theta_ej(Z0Z0e−Z0eZ0)sinθe,反映了因模式特性阻抗 Z0eZ_{0e}Z0e(或Z0oZ_{0o}Z0o)与系统参考阻抗Z0Z_0Z0 不匹配而产生的反射,其幅度随电长度θe\theta_eθe(或 θo\theta_oθo)变化。
当θe=90∘\theta_e = 90^\circθe=90∘(四分之一波长)时,cosθe=0\cos\theta_e = 0cosθe=0,Γe=Z0e2−Z02Z0e2+Z02\Gamma_e = \frac{Z_{0e}^2 - Z_0^2}{Z_{0e}^2 + Z_0^2}Γe=Z0e2+Z02Z0e2−Z02,为实数反射系数。Γ=(Zin−Z0)/(Zin+Z0)\Gamma=(Z_{in} - Z₀) / (Z_{in} + Z₀)Γ=(Zin−Z0)/(Zin+Z0)其中 Zine=Z0e2/Z0Z_{ine} = Z₀ₑ² / Z₀Zine=Z0e2/Z0
ToT_oToTeT_eTe为奇偶模二端口网络的向前传输系数,定义为boII/aoIb_o^{II} / a_o^I\quadboII/aoI beII/aeIb_e^{II} / a_e^IbeII/aeI(输出端接匹配负载 Z0Z_0Z0)。当 θe=0\theta_e = 0θe=0 时,显然Te=1T_e = 1Te=1;当 θe=90∘\theta_e = 90^\circθe=90∘ 时,Te=2j(Z0eZ0+Z0Z0e)T_e = \frac{2}{j\left(\frac{Z_{0e}}{Z_0} + \frac{Z_0}{Z_{0e}}\right)}Te=j(Z0Z0e+Z0eZ0)2,根据均值不等式在模式阻抗不等于参考阻抗时,其幅度小于 1,表明因阻抗不匹配产生反射损耗。
3.整体S参数矩阵推导
3.1计算过程
此矩阵即为对称耦合微带线四端口网络的整体 S 参数矩阵,满足互易性和对称性,可用于分析定向耦合器、滤波器等器件。
端口散射矩阵Sp\mathbf{S}_pSp 满足Bp=SpAp\mathbf{B}_p = \mathbf{S}_p \mathbf{A}_pBp=SpAp。结合变换关系:
Bp=TBm=TSmAm=TSmT−1Ap, \mathbf{B}_p = T \mathbf{B}_m = T \mathbf{S}_m \mathbf{A}_m = T \mathbf{S}_m T^{-1} \mathbf{A}_p, Bp=TBm=TSmAm=TSmT−1Ap,
故
Sp=TSmT−1. \mathbf{S}_p = T \mathbf{S}_m T^{-1}. Sp=TSmT−1.
计算 SmT−1\mathbf{S}_m T^{-1}SmT−1(略去常数因子1/21/21/2)
令 T~−1\tilde{T}^{-1}T~−1为T−1T^{-1}T−1去掉因子1/21/21/2 的矩阵,即:
T~−1=[110000111−100001−1]. \tilde{T}^{-1} = \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix}. T~−1= 101010−100101010−1 .
计算 SmT~−1\mathbf{S}_m \tilde{T}^{-1}SmT~−1:
X=[ΓeTe00TeΓe0000ΓoTo00ToΓo][110000111−100001−1]=[ΓeΓeTeTeTeTeΓeΓeΓo−ΓoTo−ToTo−ToΓo−Γo]. \begin{aligned} \mathbf{X} &= \begin{bmatrix} \Gamma_e & T_e & 0 & 0 \\ T_e & \Gamma_e & 0 & 0 \\ 0 & 0 & \Gamma_o & T_o \\ 0 & 0 & T_o & \Gamma_o \end{bmatrix} \begin{bmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\ 1 & -1 & 0 & 0 \\ 0 & 0 & 1 & -1 \end{bmatrix} \\ &=\begin{bmatrix} \Gamma_e & \Gamma_e & T_e & T_e \\ T_e & T_e & \Gamma_e & \Gamma_e \\ \Gamma_o & -\Gamma_o & T_o & -T_o \\ T_o & -T_o & \Gamma_o & -\Gamma_o \end{bmatrix}. \end{aligned} X= ΓeTe00TeΓe0000ΓoTo00ToΓo 101010−100101010−1 = ΓeTeΓoToΓeTe−Γo−ToTeΓeToΓoTeΓe−To−Γo .
计算 TSmT~−1T \mathbf{S}_m \tilde{T}^{-1}TSmT~−1 并乘以1/21/21/2即得到Sp\mathbf{S}_pSp
Sp=12[Γe+ΓoΓe−ΓoTe+ToTe−ToΓe−ΓoΓe+ΓoTe−ToTe+ToTe+ToTe−ToΓe+ΓoΓe−ΓoTe−ToTe+ToΓe−ΓoΓe+Γo] \mathbf{S}_p = \frac{1}{2} \begin{bmatrix} \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o & T_e + T_o & T_e - T_o \\ \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o & T_e - T_o & T_e + T_o \\ T_e + T_o & T_e - T_o & \Gamma_e + \Gamma_o & \Gamma_e - \Gamma_o \\ T_e - T_o & T_e + T_o & \Gamma_e - \Gamma_o & \Gamma_e + \Gamma_o \end{bmatrix} Sp=21 Γe+ΓoΓe−ΓoTe+ToTe−ToΓe−ΓoΓe+ΓoTe−ToTe+ToTe+ToTe−ToΓe+ΓoΓe−ΓoTe−ToTe+ToΓe−ΓoΓe+Γo
3.2形象理解上述矩阵运算的含义(一个计算实例)
考虑 端口1激励 (入射波 a1≠0a_1\neq0a1=0,),其余端口匹配(没有反射即没有反向入射波a2=a3=a4=0a_2=a_3=a_4=0a2=a3=a4=0)。该激励可分解为偶模和奇模的叠加(参考阻抗为(Z0Z_0Z0)):
a1=aeI+aoIa2=aeI−aoIa3=aeII+aoIIa4=aeII−aoII \begin{aligned} a_1 &= a_e^I + a_o^I \\ a_2 &= a_e^I - a_o^I \\ a_3 &= a_e^{II} + a_o^{II} \\ a_4 &= a_e^{II} - a_o^{II} \end{aligned} a1a2a3a4=aeI+aoI=aeI−aoI=aeII+aoII=aeII−aoII
考虑仅在端口1施加激励,其余端口均接匹配负载(无反射),因此端口入射波满足:
a1≠0,a2=a3=a4=0 a_1 \neq 0, \quad a_2 = a_3 = a_4 = 0a1=0,a2=a3=a4=0
{a1=aeI+aoI(1)0=aeI−aoI(2)0=aeII+aoII(3)0=aeII−aoII(4) \begin{cases} a_1 = a_e^I + a_o^I & \quad (1) \\ 0 = a_e^I - a_o^I & \quad (2) \\ 0 = a_e^{II} + a_o^{II} & \quad (3) \\ 0 = a_e^{II} - a_o^{II} & \quad (4) \end{cases} ⎩ ⎨ ⎧a1=aeI+aoI0=aeI−aoI0=aeII+aoII0=aeII−aoII(1)(2)(3)(4)
由方程(2)得aeI=aoIa_e^I = a_o^IaeI=aoI,代入方程(1)得:
aeI=aoI=a12 a_e^I = a_o^I = \frac{a_1}{2} aeI=aoI=2a1
由方程(3)和(4)联立得:
aeII=0,aoII=0 a_e^{II} = 0, \quad a_o^{II} = 0 aeII=0,aoII=0
因此,得到模态入射波:
aeI=aoI=a12,aeII=aoII=0 a_e^I = a_o^I = \frac{a_1}{2}, \quad a_e^{II} = a_o^{II} = 0aeI=aoI=2a1,aeII=aoII=0
利用模态 S 参数矩阵计算反射波:
偶模: beI=ΓeaeI=Γea12b_e^I = \Gamma_e a_e^I = \frac{\Gamma_e a_1}{2}\qquadbeI=ΓeaeI=2Γea1beII=TeaeI=Tea12b_e^{II} = T_e a_e^I = \frac{T_e a_1}{2}beII=TeaeI=2Tea1
奇模:boI=ΓoaoI=Γoa12b_o^I = \Gamma_o a_o^I = \frac{\Gamma_o a_1}{2}\qquadboI=ΓoaoI=2Γoa1boII=ToaoI=Toa12b_o^{II} = T_o a_o^I = \frac{T_o a_1}{2}boII=ToaoI=2Toa1
端口反射波为模态反射波的叠加:
b1=beI+boI=12(Γe+Γo)a1b2=beII+boII=12(Te+To)a1b3=beI−boI=12(Γe−Γo)a1b4=beII−boII=12(Te−To)a1 \begin{aligned} b_1 &= b_e^I + b_o^I = \frac{1}{2}(\Gamma_e + \Gamma_o)a_1 \\ b_2 &= b_e^{II} + b_o^{II} = \frac{1}{2}(T_e + T_o)a_1 \\ b_3 &= b_e^I - b_o^I = \frac{1}{2}(\Gamma_e - \Gamma_o)a_1 \\ b_4 &= b_e^{II} - b_o^{II} = \frac{1}{2}(T_e - T_o)a_1 \end{aligned} b1b2b3b4=beI+boI=21(Γe+Γo)a1=beII+boII=21(Te+To)a1=beI−boI=21(Γe−Γo)a1=beII−boII=21(Te−To)a1
由此得第一列 S 参数:
S11=b1a1=Γe+Γo2,S21=b2a1=Te+To2,S31=b3a1=Γe−Γo2,S41=b4a1=Te−To2 S_{11} = \frac{b_1}{a_1} = \frac{\Gamma_e + \Gamma_o}{2}, \quad S_{21} = \frac{b_2}{a_1} = \frac{T_e + T_o}{2}, \quad S_{31} = \frac{b_3}{a_1} = \frac{\Gamma_e - \Gamma_o}{2}, \quad S_{41} = \frac{b_4}{a_1} = \frac{T_e - T_o}{2} S11=a1b1=2Γe+Γo,S21=a1b2=2Te+To,S31=a1b3=2Γe−Γo,S41=a1b4=2Te−To
由于网络对称且互易,其他端口激励可类似推导,最终得到与上述对称耦合微带线四端口 S 参数矩阵一样的形式