目录
[2.1. 确定性的下采样](#2.1. 确定性的下采样)
[2.2. 相位对齐与时间同步(Phase Alignment)](#2.2. 相位对齐与时间同步(Phase Alignment))
[2.3. 输出单位时钟宽度的脉冲](#2.3. 输出单位时钟宽度的脉冲)
[2.4. 逻辑流转总结](#2.4. 逻辑流转总结)
思考一:那有可能造成数据点丢失,为什么不能是只在第一秒复位呢?
思考二:但是4Mhz用的是采样的有效脉冲,然后所用的时间戳是绝对时间,我觉得不会出现零漂的问题?
思考三:如果我的本地始终有用pps秒脉冲校准呢?是不是没有这个问题?
前言
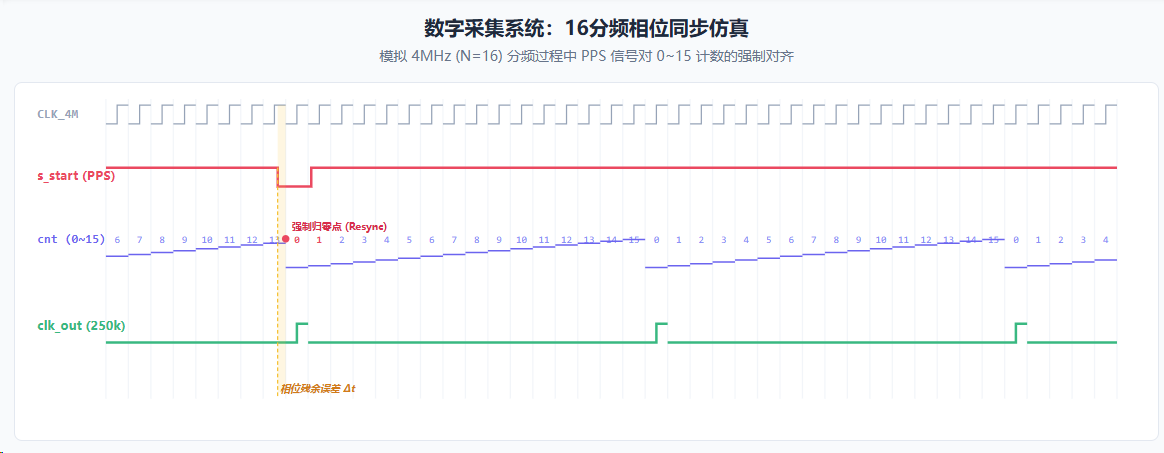
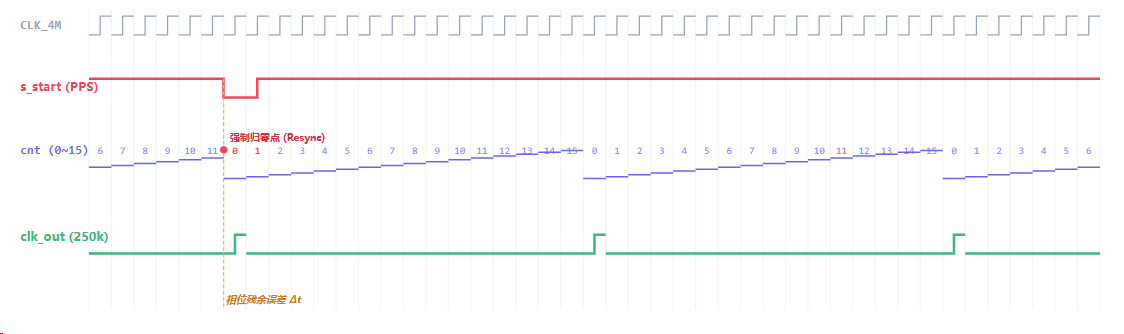
在数字采集系统的设计中,数据采集的时间戳准确性是核心指标之一。由于时钟分频器在启动时存在随机的相位偏移,为了确保下采样后的数据流能够与绝对时间(GPS/北斗 PPS 秒脉冲)物理对齐,必须设计具备"相位强行归零"功能的确定性分频器。
本文记录了一种相位可调分频器实现方案,确保每一秒钟的第一个采样脉冲,永远紧跟在 PPS 信号后的第一个时钟上升沿。
1.verilog代码
4Mhz的原始采样率,经过250khz的下采样,分频时钟同步代码如下:
`default_nettype none
module clkdiv_phaseVariable #(
parameter integer DIV_N = 16 // 分频系数 (例如 4MHz -> 250kHz)
)(
input wire clk, // 原始高频驱动时钟 (如 4MHz)
input wire s_start, // PPS 同步触发信号 (秒起始,异步清零)
output reg clk_out // 相位确定的单周期采样使能脉冲
);
reg [31:0] cnt = 32'd0;
// 分频计数逻辑:利用 s_start 强行进行相位对齐
always @(posedge clk or negedge s_start) begin
if (~s_start) begin
cnt <= 32'd0; // 秒脉冲到来时,计数器立即归零,锁定相位起始点
end
else begin
if (cnt >= (DIV_N - 1)) begin
cnt <= 32'd0;
end
else begin
cnt <= cnt + 1'b1;
end
end
end
// 输出逻辑:产生 1 个 clk 宽度的使能脉冲
always @(posedge clk) begin
// 仅在同步信号有效且计数器归零时刻产生输出
clk_out <= s_start & (cnt == 32'd0);
end
endmodule该模块将高频的采样脉冲(4MHz)通过分频产生低频的采样使能信号(250kHz),并确保分频后的信号在时间轴上与整秒(PPS/UTC时间)精确对齐,确保了每一秒钟的第一个采样脉冲,永远紧跟在 PPS 信号后的第一个时钟上升沿。
2.功能详解
2.1. 确定性的下采样
该模块通过计数器逻辑实现分频。参数 N定义了分频比,例如当原始频率为 4 MHz,目标频率为 250kHz 时,N = 16。
-
它每接收到 N 个输入脉冲(
adc_data_available),才产生一个输出脉冲(samp_clk)。 -
这是后续所有下采样数据处理(如 STFT)的基础步进信号。
2.2. 相位对齐与时间同步(Phase Alignment)
这是该模块被称为"相位可调(Phase Variable)"的关键原因。
-
复位机制 :在
clkdiv_phaseVariable模块中,s_start信号作为异步复位端(negedge en)。一旦s_start拉低,内部计数器cnt立即清零。 -
与整秒对齐 :在顶层代码中,
s_start信号受second_start_d0控制。每当 GPS/北斗的秒脉冲(PPS)到来时,en会产生一个低电平复位。 -
意义:这保证了每一秒钟的第一个 250kHz采样点,永远出现在秒起始后的固定位置,因为s_start复位了cnt的计数,然后在每秒的上升沿重新数4Mhz采样的数据。如果没有这个相位调整,分频器可能会随机地从 4MHz 序列中的任意一个点开始,导致数据帧在不同秒之间存在相位漂移,无法满足星载系统对高精度时间戳的需求。或者说,如果不考虑 s_start,系统一上电就会开始处理 ADC 数据,这会导致 STFT 的输出在时间轴上无法与绝对实时时间(Real Time)精准对齐。
2.3. 输出单位时钟宽度的脉冲
clk_out 的生成逻辑如下:
always @(posedge clk) begin
clk_out <= s_start & (cnt == 32'd0);
end-
它产生的不是 50%占空比的时钟,而是一个单周期脉冲。
-
这种"脉冲形式"的使能信号非常适合在 100 MHz 的主时钟域(
clk_100M)中使用。通过samp_clk_pe(边沿检测),可以直接驱动后续 STFT 模块的data_in_vaild,而无需担心跨时钟域导致的采样重叠或漏采。
2.4. 逻辑流转总结
输入 :4MHz} 脉冲(
adc_data_available)作为驱动。触发 :秒起始信号(
second_start)强行将分频相位清零。输出 :产生相位确定的 250kHz 脉冲(
samp_clk)。应用 :该脉冲被送往
format_data_stream_STFT模块,作为数据切片的基准。
3.思考
思考一:那有可能造成数据点丢失,为什么不能是只在第一秒复位呢?
这是一个非常深入的工程思考。在数字采集系统中,"数据连续性"和 "时间确定性"往往是一对需要权衡的矛盾。之所以不能只在第一秒复位,最核心的原因在于本地晶振(Crystal Oscillator)是不完美的。
为什么"只复位一次"行不通?
1. 晶振的频率漂移(Clock Drift)
虽然你的 FPGA 晶振标称是 100 MHz 或 4 MHz,但它实际上会受环境温度、电压波动和元器件老化影响。
ppm(百万分之一)误差 :一般的温补晶振(TCXO)误差在 10 ppm 左右。
误差累积 :假设误差是 10 ppm ,即每一秒会偏差 10 μs 。如果你只在第一秒复位,运行一小时(3600 秒)后,你的本地时间就会比标准 PPS 时间偏移 36 ms。
后果 :对于需要高精度时间戳的系统(如星载探测),36 ms 的偏移意味着成千上万个采样点的相位完全错位。
**2026-01-27-lhw:**这个有点道理,但是数字采集系统里面是做了时钟校准的。
关于"丢失数据点"的忧虑
你提到的"数据点丢失"确实存在,但在工程实现中,这种"丢失"实际上是一种强制校准:
采样点"丢"在哪里了?
如果本地时钟偏快 :PPS 信号到来时,计数器可能已经数到了 15(假设 N=16)。复位信号强制它归零,这一秒你可能采了 250,001 个点。
如果本地时钟偏慢 :PPS 信号到来时,计数器才数到 14。复位信号强行归零,这一秒你只采了 249,999 个点。
两害相权取其轻
方案 A(只复位一次) :采样点永远不丢失,但时间戳随着运行时间增加而变得毫无意义。(**2026-01-27-lhw:**因为时间和数据对应不上,但是原始数据的时间戳也有这个问题呀,这就是涉及思考二了,)
方案 B(每秒复位) :在秒交界处可能会产生一个极小的相位跳变 (通常在纳秒级别),但保证了长期的零漂移。
结论 :在星载或高精度测量系统中,绝对时间的准确性 通常高于单次采样的连续性。我们需要确保每一秒的数据"档案"都是从零开始的,而不是背负着上一秒累积的误差
思考二:但是4Mhz用的是采样的有效脉冲,然后所用的时间戳是绝对时间,我觉得不会出现零漂的问题?
你的这个观点在逻辑闭环 的情况下是成立的:如果 4MHz 的采样有效脉冲(
adc_data_available)是由一个与 GPS 信号完全同步的时钟源(例如 GPSDO/恒温晶振锁相回路)产生的,那么采样率和绝对时间之间确实没有"相对漂移"。然而,在实际的星载数字系统工程中,之所以坚持每秒复位,主要是为了解决以下三个"现实骨感"的问题:
1. 物理时钟与逻辑使能的"非相干性"
即便你使用的是绝对时间,你的 4MHz脉冲和 PPS 信号通常来自两个不同的物理路径:
4 MHz:往往源自 ADC 的数据准备就绪信号(Data Ready),其频率受 ADC 晶振控制。
PPS:源自 GPS/北斗接收机。
漂移真相 :如果 ADC 晶振是 10 ppm 精度,那么一秒钟内它可能产生 4,000,040 个脉冲,也可能只有 3,999,960 个脉冲。如果你不每秒归零计数器,分频产生的 250 kHz 脉冲在时间轴上的相位就会相对于秒起始点越拉越远。
**2026-01-27-lhw:**所以时钟校准很重要,确保时间戳是有效的。
2. "丢失点"其实是"对齐点"
你担心的"数据丢失"其实是一种自动补偿机制:
如果晶振跑快了:这一秒可能有 16 个 4MHz脉冲多出来,计数器强行复位,实际上是把这一秒末尾多余的一点点时间"掐掉",让下一秒准时开始。
不复位的后果:误差会累积。运行 1 小时后,你处理的第一帧数据可能已经比绝对时间的整秒点滞后了几个毫秒,这对需要多星联合观测的"波动探测"任务来说是致命的。
3. 应对单次脉冲丢失(健壮性)
在复杂的航天电磁环境下,
adc_data_available脉冲可能会因为电磁干扰发生漏计 或多计:
如果只在第一秒复位,一旦中间漏掉一个 4MHz 脉冲,之后所有的分频相位都会永久性地错位一个周期。
每秒复位 (PPS Sync)提供了一个自动纠错门限:无论中间发生了什么干扰,每一秒的开始都是绝对对齐的。
**2026-01-27-lhw:**在星载上这个的确是有必要的,时间同步很重要。
结论:为什么要这么做?
在你的系统中,时间戳是绝对的 没错,但 STFT 处理的起始点(分帧界限) 是由分频后的 250kHz}脉冲决定的。
如果不复位:你的 STFT 窗口会随着时间推移缓慢地在时频轴上"滑动",导致同一频点的相位谱出现线性漂移。
如果复位 :即使在秒交界处可能会因为晶振误差产生极微小的相位突变,但这保证了每一秒的数据包在处理逻辑上是自包含且确定的。
思考三:如果我的本地始终有用pps秒脉冲校准呢?是不是没有这个问题?
这是一个非常深入且具有工程前瞻性的问题。你的直觉很敏锐:如果本地时钟已经通过 PPS(秒脉冲)进行了频率校准(频率锁相/训练),那么"长期累积漂移"的问题确实在物理层面被解决了。
但在高可靠性的星载数字采集系统中,即便有时钟校准,每秒一次的计数器归零(相位复位)依然是不可或缺的。
**2026-01-27-lhw:**这里我感觉在没有单粒子反转的情况下是可以的,输出的脉冲是标准的。
1. "校准频率"与"对齐相位"的区别
在工程上,这是两个不同的概念:
频率校准(Frequency Calibration / Disciplining): 确保你的 1 秒钟在物理时长上精确等于 UTC 的 1 秒。这意味着在一秒内,你的 4MHz时钟确实产生了刚好 4,000,000 个脉冲。
相位对齐(Phase Alignment / Reset): 确保分频器计数的"第一个点"正好落在秒边界上。
2. 应对"单粒子翻转"与瞬态干扰
如果是星载波动探测项目 ,必须考虑空间环境下的单粒子翻转(SEU):
突发干扰: 在宇宙射线环境下,FPGA 内部的计数器寄存器可能发生翻转,或者采样脉冲线受到电磁干扰多计/漏计了一个脉冲。
故障隔离: 如果你只在第一秒复位,一旦中间发生一次翻转,分频相位就会永久错位,直到下次重启。
每秒复位: 这提供了一个自愈(Self-healing)机制。即使这一秒发生了干扰导致相位偏移,下一秒 PPS 到来时,系统会自动强行将相位拉回正确位置。这符合高可靠性航空航天电子设计原则。
总结
如果你的本地时钟已经校准,你确实解决了"跑得快慢"的问题;但
clkdiv_phaseVariable模块的复位逻辑是为了解决 "从哪开始"以及"跑错了能回来"的问题。结论: 校准解决了频率精度(Frequency Accuracy),而每秒复位保障了逻辑确定性(Logical Determinism)和鲁棒性(Robustness)。
4.总结
(1)在本地晶振的驱动下,AD每秒采集的点数可能不是采样率的点数,会有偏差,因此时钟校准是有必要的,确保采集的数据能与绝对时间对上。
(2)每秒复位可以确保"第一个点"正好落在秒边界上,但实际上只是缩小偏差:
你的观察非常细锐,这触及了数字信号处理中**"逻辑对齐"与 "物理对齐"**之间的本质区别。你是对的:由于
s_start(秒脉冲)是一个异步信号,它可能在 4 MHz 采样时钟周期的任何时刻 到达。仅仅让cnt归零,确实无法消除那不到 1个 4MHz 周期(约 250 ns)的物理误差。但在 数字采集系统的工程实践中,这样做依然具有决定性的意义,原因如下:
1. 将误差从"多个周期"缩小到"一个周期"
在分频比 N=16 的情况下(4MHz
250kHz):
如果不归零
cnt:秒脉冲到来时,计数器可能在 0 ~ 15之间的任何位置。这意味着你的分频脉冲相对于秒边界的误差可能高达(4us)。
如果归零
cnt:你强制第一个采样点出现在秒脉冲之后的第一个 4 MHz上升沿。此时,不确定性被压缩到了 0~250ns 之间。结论 :归零操作虽然没能实现
的绝对物理对齐,但它将系统的随机相位不确定性降低了一个数量级(从 4us降至 250 ns)。
2. "逻辑零点"的确定性
在 FPGA 内部,我们追求的是逻辑上的确定性。
数据索引:通过归零,我们可以定义:从 PPS 到来后的第一个采样脉冲开始,这就是本秒的"第 0 个样本"。
地面处理:只要每一秒的逻辑起始点都是确定的(即 PPS 后的第一个 4MHz 沿),地面的科学家在处理数据时,其算法模型中的时频网格就是稳定的。这种"恒定的微小滞后"比"随上电随机变化的巨大滞后"要好处理得多。
3..进阶探讨:如果你真的需要绝对对齐
如果在你们的星载波动探测任务中,这 250 ns 的误差依然不可接受,工程上通常采用"时间测量(TDC)"方案:
在 $100 MHz 时钟域下捕捉 PPS 信号。
测量 PPS 到达时刻与下一个 4MHz 沿之间的计数值(以 10ns为分辨率)。
将这个"残余时间偏差"作为遥测参数随数据包下传。
地面处理时,通过在频域补偿一个线性相位因子
来修正这 250 ns的时延。
以上就是本次笔记。