探索自动避障路径选择：Matlab 路径规划算法与仿真实践

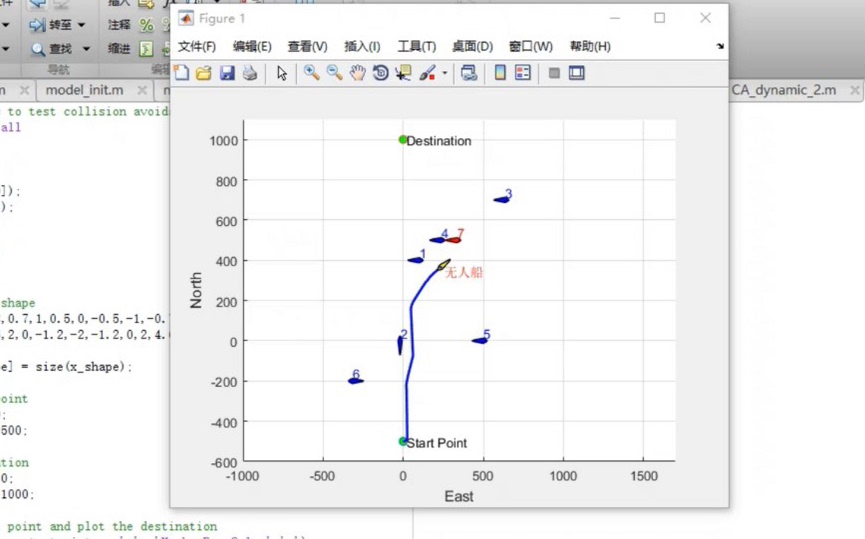
自动避障路径选择 Matlab路径规划算法自己研究编写路径规划仿真

在智能系统的领域中，自动避障路径选择是一个极其关键的问题。无论是自动驾驶汽车在复杂道路上穿梭，还是机器人在充满障碍物的环境中执行任务，高效且准确的路径规划算法都是实现安全与智能运行的核心。今天，咱们就来聊聊用 Matlab 实现路径规划算法，并进行相关仿真的有趣过程。

Matlab：路径规划的得力工具

Matlab 凭借其丰富的工具箱和强大的数值计算能力，成为了路径规划算法研究与实现的绝佳平台。它提供了各种便捷的函数和可视化工具，让我们可以轻松地构建模型、编写算法并进行仿真验证。

自己动手编写路径规划算法

咱们以一个简单的基于 A算法的自动避障路径规划为例。A 算法结合了 Dijkstra 算法的广度优先搜索策略和贪心算法的最佳优先搜索策略，能在搜索空间中找到从起点到终点的最优路径，同时巧妙避开障碍物。

下面是一个简化的 A* 算法 Matlab 代码示例：

matlab 复制代码

% 定义地图尺寸和障碍物位置
map_size = [100, 100];
obstacles = [20:30, 50:60]; % 假设障碍物位置

% 起点和终点
start = [10, 10];
goal = [90, 90];

% 初始化代价和父节点数组
g_score = inf(map_size(1), map_size(2));
g_score(start(1), start(2)) = 0;
f_score = inf(map_size(1), map_size(2));
f_score(start(1), start(2)) = heuristic(start, goal);
came_from = zeros(map_size(1), map_size(2), 2);

open_set = [start];

while ~isempty(open_set)
    % 找到 f_score 最小的节点
    [~, current_index] = min(f_score(sub2ind(map_size, open_set(:, 1), open_set(:, 2))));
    current = open_set(current_index, :);

    if all(current == goal)
        % 找到了路径，回溯生成路径
        path = [];
        while ~all(current == start)
            path = [current; path];
            current = came_from(current(1), current(2), :);
        end
        path = [start; path];
        break;
    end

    open_set(current_index, :) = [];

    % 检查邻居节点
    for dx = -1:1
        for dy = -1:1
            neighbor = current + [dx, dy];
            if neighbor(1) >= 1 && neighbor(1) <= map_size(1) && neighbor(2) >= 1 && neighbor(2) <= map_size(2) &&...
                    ~ismember(neighbor(1), obstacles) && ~ismember(neighbor(2), obstacles)
                tentative_g_score = g_score(current(1), current(2)) + 1;

                if tentative_g_score < g_score(neighbor(1), neighbor(2))
                    came_from(neighbor(1), neighbor(2), :) = current;
                    g_score(neighbor(1), neighbor(2)) = tentative_g_score;
                    f_score(neighbor(1), neighbor(2)) = tentative_g_score + heuristic(neighbor, goal);
                    if ~ismember(neighbor, open_set, 'rows')
                        open_set = [open_set; neighbor];
                    end
                end
            end
        end
    end
end

function h = heuristic(a, b)
    h = abs(a(1) - b(1)) + abs(a(2) - b(2));
end

代码分析

地图与参数初始化 ：
- 我们首先定义了地图的尺寸 mapsize*，这里设置为 100x100 的网格。同时，定义了障碍物所在的位置 obstacles，这里简单设定了两个区域为障碍物。起点 start 和终点 goal 也被明确设定。
- 初始化了 g* score（从起点到当前节点的实际代价）、fscore*（从起点经过当前节点到终点的估计总代价）和 came* from（记录路径上每个节点的父节点）数组。open_set 用于存储待探索的节点。

主循环 ：
- 在 while 循环中，只要 openset**不为空，就不断从 open set 中选取 f*score**最小的节点 current。
- 如果当前节点就是终点，说明找到了路径，通过回溯 came* from 数组生成最终路径。
- 否则，检查当前节点的邻居节点。邻居节点在地图范围内且不在障碍物位置时，计算从起点到邻居节点的试探性代价 tentativegscore。
- 如果这个试探性代价小于邻居节点当前记录的 gscore*，则更新邻居节点的 came* from、gscore**和 f score，并将邻居节点加入 open_set。

启发式函数 ：
- heuristic 函数用于估计从当前节点到终点的代价。这里采用曼哈顿距离作为启发式函数，简单计算两个节点在横纵方向上的距离之和。

路径规划仿真

有了算法代码，接下来就是进行仿真，看看我们规划的路径效果如何。Matlab 的可视化功能可以帮助我们将路径直观地展示出来。

matlab 复制代码

% 绘制地图和路径
figure;
hold on;
for i = 1:size(obstacles, 2)
    rectangle('Position', [obstacles(i), 1, 1, map_size(2)], 'FaceColor', 'r');
end
for i = 1:size(path, 1)
    plot(path(i, 2), path(i, 1), 'bo - ');
end
plot(start(2), start(1), 'go', 'MarkerSize', 10);
plot(goal(2), goal(1), 'ro', 'MarkerSize', 10);
xlabel('X 坐标');
ylabel('Y 坐标');
title('自动避障路径规划仿真');
axis([1 map_size(2) 1 map_size(1)]);
hold off;

仿真分析

这段代码利用 Matlab 的图形绘制函数，将地图中的障碍物用红色矩形表示，规划出的路径用蓝色线条和圆圈表示，起点用绿色圆圈，终点用红色圆圈。通过这个简单的可视化，我们可以直观地看到路径规划算法是否成功避开了障碍物，并找到了从起点到终点的合理路径。

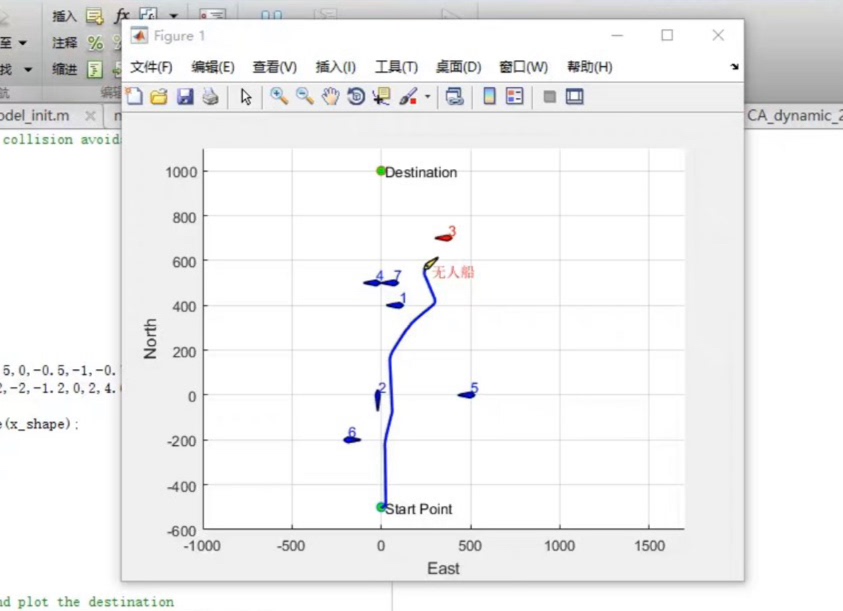
自动避障路径选择 Matlab路径规划算法自己研究编写路径规划仿真

在实际应用中，还可以进一步优化算法，比如采用更复杂的启发式函数，或者针对不同的环境特点对算法进行调整。同时，仿真过程也可以添加更多的细节，比如动态障碍物的处理等。

通过自己研究编写路径规划算法并用 Matlab 进行仿真，不仅能深入理解路径规划的原理，还能为实际应用打下坚实的基础。希望大家都能在这个有趣的领域中发现更多好玩的东西！