数据结构-并查集

1.并查集概念
2.并查集的实现

🌟🌟hello，各位读者大大们你们好呀🌟🌟

🚀🚀系列专栏：【Qt的学习】

📝📝本篇内容：并查集概念;并查集的实现

⬆⬆⬆⬆上一篇：经典排序算法(五万字详解，全网最细)

💖💖作者简介：轩情吖，请多多指教(>> •̀֊•́ ) ̖́-

1.并查集概念

在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find set)，可以把它看做是一个森林，每一个集合是树。

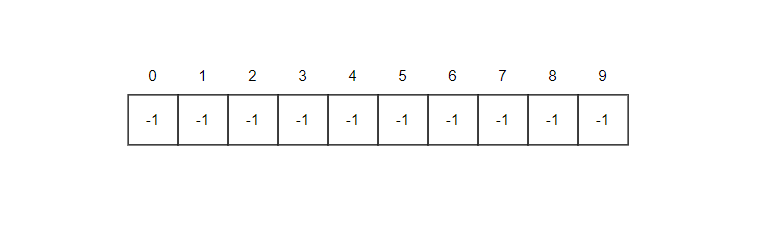
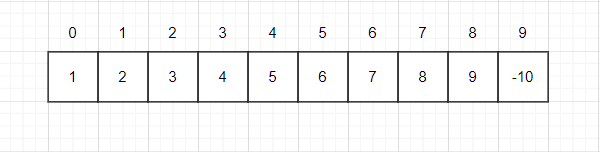
例如刚开学，有好多的新同学，大家一开始都不认识，因此各自一个集合，给每个同学编号，即0-9，数组中的数字代表该小集体中具有的成员个数

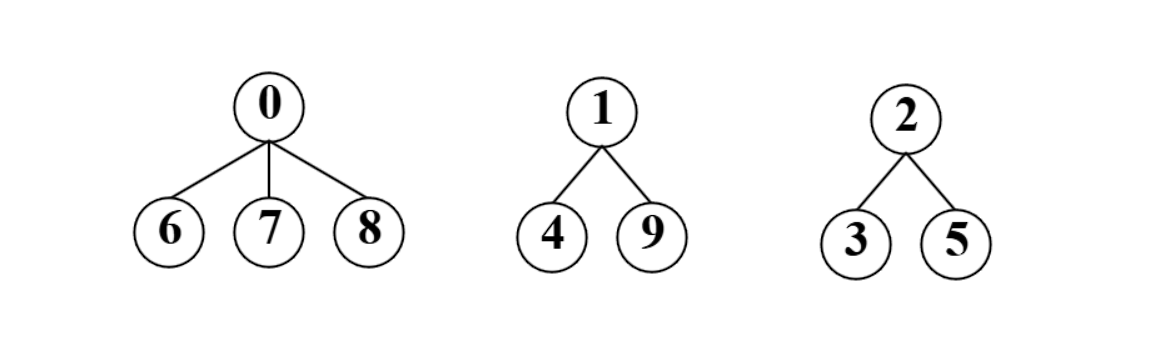
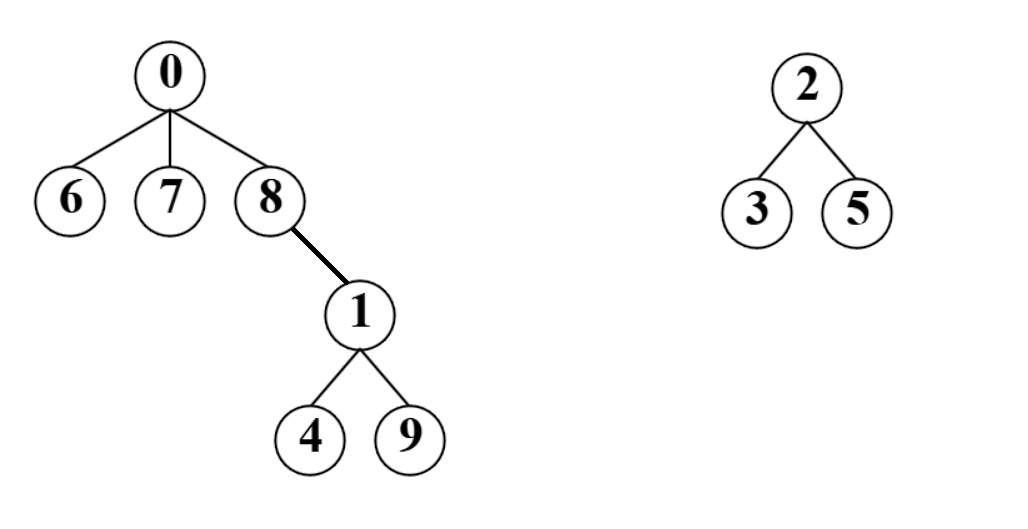
接下来随着小组作业要分组，大家就开始认识了，并且选出了组长0,1,2，下面是集合用树型表示的方法

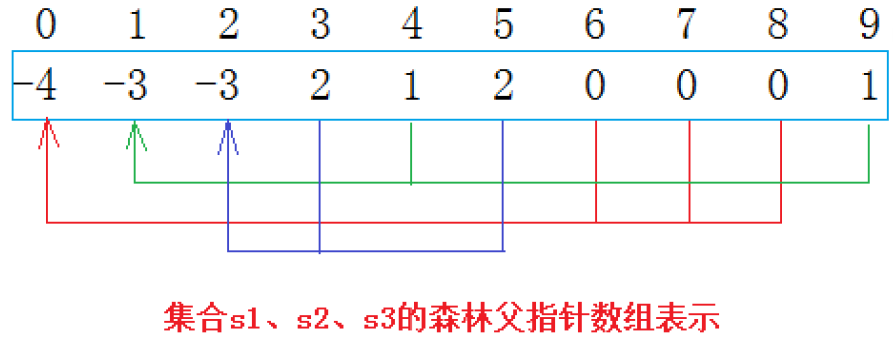
在数组上反应就是像上图一样的情况，并且我们对它进行实现的时候，也是通过vector来实现的。

通过观察上面的数组我们可以发现：

①数组的下标对应集合中元素的编号

②数组中如果为负数，负号代表根结点，数字代表该集合中的元素个数

③数组中如果为非负数，代表该元素的双亲在数组中的下标

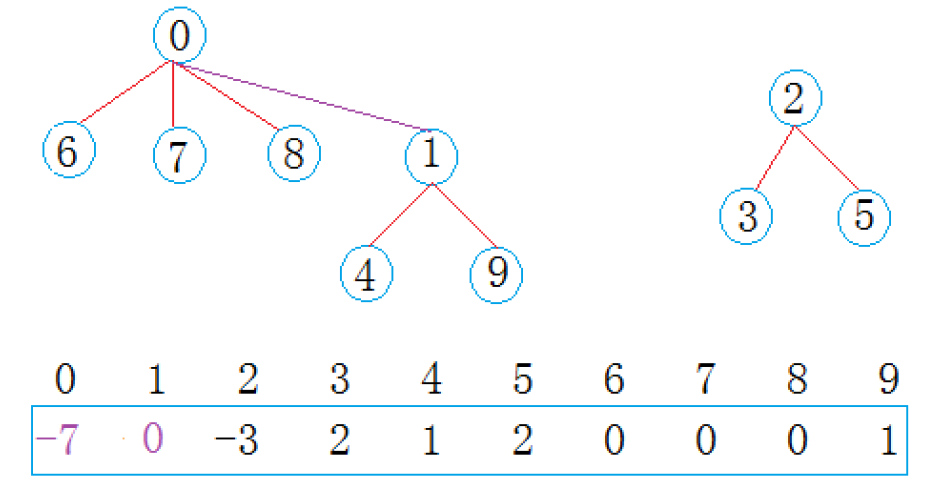
当然还是有可能继续合并成一个集合，这这种情况下，原本作为组长的1变成了0的组员，那么它的对应下标存储的内容应该加到0下标的位置上去，使得0成为根结点，0集合中一共有7个结点，而1下标所存储的内容应该变成它的父结点0

2.并查集的实现

cpp 复制代码

#pragma once
#include <vector>
using namespace std;
class UnionFindSet
{
public:
	UnionFindSet(size_t size)//构造函数
		:_ufs(size, -1)//10个位置初始化为-1
	{}

	//找根结点
	size_t FindRoot(int x)
	{
		int parent = x;
		while (_ufs[parent] >= 0)//循环找到根
		{
			parent = _ufs[parent];
		}

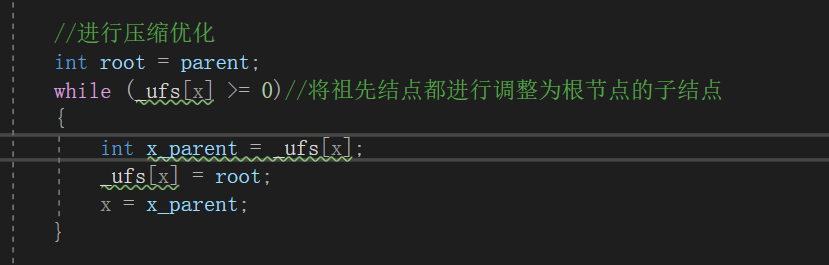
		//进行压缩优化
		int root = parent;
		while (_ufs[x] >= 0)//将祖先结点都进行调整为根节点的子结点
		{
			int x_parent = _ufs[x];
			_ufs[x] = root;
			x = x_parent;
		}
		
		return parent;//返回根结点
	}

	//并集
	void Union(int x1, int x2)
	{
		int root1 = FindRoot(x1);
		int root2 = FindRoot(x2);
		if (InSet(x1, x2))//如果已经在一个集合里了
		{
			return;
		}
		else
		{
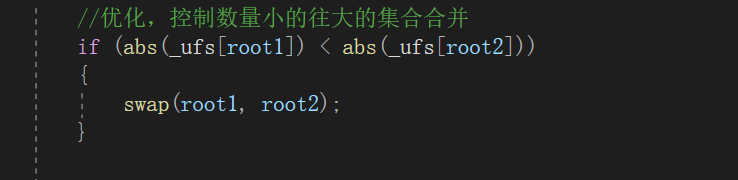
			//优化，控制数量小的往大的集合合并
			if (abs(_ufs[root1]) < abs(_ufs[root2]))
			{
				swap(root1, root2);
			}


			_ufs[root1] += _ufs[root2];
			_ufs[root2] = root1;

		}
	}

	//有几个集合
	size_t setCount()
	{
		size_t count = 0;
		for (int i = 0; i < _ufs.size(); i++)
		{
			if (_ufs[i] < 0)//<0的都是根
			{
				count++;
			}
		}
		return count;
	}

	//在不在一个集合
	bool InSet(int x1, int x2)
	{
		return FindRoot(x1) == FindRoot(x2);
	}


private:
	vector<int> _ufs;//并查集
};

cpp 复制代码

#define _CRT_SECURE_NO_WARNINGS 1
#include <iostream>
#include "UnionFindSet.hpp"
using namespace std;
int main()
{
	UnionFindSet s(10);
	/*cout << s.FindRoot(7) << endl;
	cout << s.FindRoot(9) << endl;
	s.Union(7, 9);
	cout << s.FindRoot(7) << endl;
	cout << s.FindRoot(9);*/

	//根结点没有变化，一直是9--没有优化
	/*s.Union(9, 8);
	s.Union(8, 7);
	s.Union(7, 6);
	s.Union(6, 5);
	s.Union(5, 4);
	s.Union(4, 3);
	s.Union(3, 2);
	s.Union(2, 1);*/


	//根结点不停地发生了变化-根结点为合并本身
	s.Union(8, 9);
	s.Union(7, 8);
	s.Union(6, 7);
	s.Union(5, 6);
	s.Union(4, 5);
	s.Union(3, 4);
	s.Union(2, 3);
	s.Union(1, 2);
	s.FindRoot(9);//没有合并中的优化就需要手动使用FindRoot中的优化来降低深度


	return 0;
}

这里主要是要讲一下它的压缩优化情况，这个地方主要是为了优化"单支树"的情况包括深度太深，使得所有的结点变成根结点的子结点。当我们只要FindRoot这个函数就会进行优化

第二个优化的地方是为了降低深度，如下面第二张图，并且能够在FindRoot中的优化没有起效果的时候（示例中的根结点为合并本身的情况），进行优化"单支树"的情况来降低深度

如图，为的是希望在合并时，是右边合并到左边，这样就不会使得深度更深。

但是并不是说有了第二个优化就可以不需要第一个优化了，当两棵树（两个集合）都不止有一个元素时，想要更好的优化，就需要通过第一个优化方式，进行挨个压缩到与根结点进行相连，因此两个优化是相辅相成的，总得来说优化就是为了降低深度，提高查找根结点的效率。
🌸🌸数据结构-并查集大概就讲到这里啦，博主后续会继续更新更多Qt的相关知识，干货满满，如果觉得博主写的还不错的话，希望各位小伙伴不要吝啬手中的三连哦！如有小伙伴需要Qt的安装包可以私信我，你们的支持是博主坚持创作的动力！💪💪