大模型架构算力对比：Decoder-only、Encoder-Decoder、MoE深度解析.71

一、概念回顾

• **算力：**这里特指模型训练/推理时消耗的计算资源，通常以 FLOPs（浮点运算次数，每秒浮点运算数为 TFLOPs/PFLOPs）衡量，也可理解为模型完成一次计算任务需要的计算工作量。
• **注意力机制：**大模型的核心大脑，负责捕捉文本/数据中的上下文关联，是算力消耗的核心来源之一，不同架构的注意力机制设计差异极大。
• **参数量：**模型中可训练的参数（权重、偏置等）的总数，通常以 B（十亿）为单位，参数量≠算力，但同等条件下参数量越大，算力消耗通常越高。
• **计算密度：**单位计算资源（如显存、算力核心）能处理的有效计算量，简单说是否把算力用在刀刃上，计算密度越高，算力利用率越高，同等任务消耗越低。
• **激活稀疏性：**模型训练/推理时，只有部分神经元（或模块）被激活参与计算，其余处于休眠状态，不消耗算力，是 MoE 模型节省算力的核心逻辑。
• **KV 缓存：**推理阶段缓存注意力机制中的 Key（K）和 Value（V），避免重复计算，提升推理速度，但长文本场景下 KV 缓存会急剧膨胀，占用大量显存，间接推高算力成本。

二、三种架构的定位

1. Decoder-only（仅解码器）架构

代表模型： GPT 系列、LLaMA 系列、Qwen 系列等。
主要应用场景： 自然语言生成任务，包括智能对话、文本创作、内容摘要、代码生成等。
核心特点：

• 采用纯自回归方式，仅使用解码器结构，逐词预测下一个 token；
• 架构简洁，计算路径短，推理效率高；
• 依赖强大的注意力机制捕捉上下文信息，在生成流畅性和连贯性上表现优异；
• 是当前主流对话大模型（如 ChatGPT、通义千问）的基础架构。

2. Encoder-Decoder（编解码器）架构

代表模型： T5、BART、早期 Transformer 机器翻译模型等。
主要应用场景： 序列到序列（Seq2Seq）任务，如机器翻译、文本摘要（尤其是抽取+生成结合）、问答系统、文本改写等。
核心特点：

• 由编码器和解码器两部分组成：编码器理解输入语义，解码器基于该语义生成目标输出；
• 输入与输出可长度不同，适合"转换型"任务；
• 理解与生成能力均衡，对复杂语义映射任务更具优势；
• 训练通常采用"掩码-重建"或"输入-输出对"范式，泛化能力强。

3. MoE（混合专家）架构

代表模型： Switch Transformer，以及据信用于 GPT-4 的稀疏激活结构。
主要应用场景： 超大规模语言模型，参数达千亿甚至万亿级，用于需要极致知识容量与多任务泛化能力的场景。
核心特点：

• 每一层包含多个"专家"子网络，但每次前向传播仅激活其中一小部分（如 1--2 个）；
• 实现"参数量巨大但计算量可控"的稀疏激活机制；
• 在不显著增加推理成本的前提下，大幅提升模型容量和性能；
• 是大模型迈向高性价比扩展的关键技术路径，尤其适合云侧部署的超大模型服务。

三、三种架构的算力消耗

算力消耗的核心差异集中在 3 个维度：注意力机制设计、参数量规模、计算密度，我们逐个拆解，由浅入深。

1. 注意力机制

注意力机制的算力复杂度，关键是先明确一个基础公式：

注意力机制算力复杂度 ≈ O (n² × d)

其中 n 是上下文长度（文本长度），d 是模型隐藏层维度。

由公式可知：上下文长度 n 对算力的影响是"平方级"的，长文本场景下会成为算力黑洞，而三种架构的注意力机制设计，直接决定了这个复杂度的实际落地值。

1.1 Decoder-only 架构的注意力机制

采用因果掩码自注意力，核心特点：

• 只能关注前文，不能关注后文，符合自然语言生成的逻辑，比如写句子只能从左到右。
• 注意力计算是"自包含"的，即输入序列自身与自身计算注意力，无需额外输入。
• 算力复杂度：严格遵循 O (n² × d)，但推理阶段可通过 KV 缓存优化，将后续步骤的注意力算力复杂度降至 O (n × d)，这是 Decoder-only 推理友好的核心原因。
• 技术细节：掩码（Mask）的作用是屏蔽后文信息，避免模型 "提前看到" 结果，这个掩码操作几乎不消耗额外算力，只是对计算矩阵进行简单的 "遮挡" 处理，相比 Encoder-Decoder 少了跨序列注意力计算，算力更集中。

1.2 Encoder-Decoder 架构的注意力机制

• 采用 双注意力机制：Encoder 端的"双向自注意力" + Decoder 端的"因果掩码自注意力 + 编码器 - 解码器跨注意力"。
• Encoder 端：双向自注意力，能关注整个输入序列的前后文（适合理解文本，比如翻译时看懂整句话），算力复杂度 O (n₁² × d)（n₁ 是输入序列长度）。
• Decoder 端：
  • 因果掩码自注意力，关注 Decoder 自身的前文，算力复杂度 O (n₂² × d)（n₂ 是输出序列长度）；
  • 跨注意力，关注 Encoder 端的输出结果，算力复杂度 O (n₁ × n₂ × d)（无平方级，是线性乘积累加）。
• 整体算力复杂度：O (n₁² × d + n₂² × d + n₁ × n₂ × d)，明显高于同等参数量、同等任务长度下Decoder-only 架构。
• 技术细节：跨注意力是额外的算力消耗点，它需要建立 Decoder 输出序列与 Encoder 输入序列的关联，比如机器翻译中，英文输出需要对应中文输入的每个词，这个过程需要额外的矩阵乘法计算，且无法通过 KV 缓存进行大幅优化，因为输入序列（n₁）和输出序列（n₂）通常是不同的。

1.3 MoE 架构的注意力机制

MoE 不是替代前两种架构，而是在 Decoder-only 或 Encoder-Decoder 基础上的模块升级，其注意力机制本身与基础架构一致，比如Switch Transformer 是 Decoder-only+MoE。

• 核心差异：注意力机制的计算只在"激活的专家模块"中进行，未激活的专家模块不参与注意力计算，因此实际算力消耗是"稀疏化"的 O (s × n² × d)，s是稀疏系数，0 < s < 1，通常远小于1。
• 技术细节：MoE 的注意力算力节省不是来自注意力机制本身的优化，而是来自专家模块的稀疏激活，但它额外增加了"门控网络"的算力消耗，用于选择哪些专家模块被激活，门控网络的算力复杂度通常是 O (n × k)（k 是专家数量），相比注意力算力可以忽略，但专家数量过多时，门控网络的消耗也会凸显。

2. 参数量

2.1 Decoder-only 架构

• 参数量规模：通常是紧凑型，比如GPT-3是175B，LLaMA2是70B，参数量全部参与训练或推理，参数密集激活，即每一个参数都在干活。
• 算力与参数量的关系：近似线性正相关，参数量翻倍，在训练阶段的算力消耗也近似翻倍。
• 技术细节：Decoder-only 架构没有额外的冗余参数，所有参数都服务于生成任务，计算密度较高，因此在同等参数量下，其算力利用率是三者中较高的。

2.2 Encoder-Decoder 架构

• 参数量规模：通常是双模块型，Encoder 和 Decoder 各有一套参数，整体参数量比同等性能的 Decoder-only 架构略高。
• 算力与参数量的关系：参数量更高，且由于双注意力机制的额外消耗，算力消耗与参数量的正相关系数更高，即参数量翻倍，算力消耗可能翻倍以上。
• 技术细节：Encoder 和 Decoder 是两个相对独立的模块，部分参数无法共享，比如注意力层的参数，导致参数量冗余度略高于 Decoder-only，计算密度略低。

2.3 MoE 架构

• 参数量规模：超大容量型，比如 Switch Transformer 可以轻松达到万亿级参数量，远超前两种架构，但只有少量参数被激活的专家模块参与训练或推理。
• 算力与参数量的关系：参数量与算力消耗解耦，参数量可以大幅增加（提升模型能力），但算力消耗只随激活参数量增加而增加，比如 1 万亿参数的 MoE 模型，激活参数量可能只有 100B，算力消耗与 100B 参数量的密集模型相当。
• 技术细节：MoE 模型的专家模块是并行化设计的，每个专家模块都是一个小型的 Transformer 子模块，门控网络根据输入内容选择少数专家（通常 2-4 个）参与计算，未被选择的专家模块的参数不更新、不参与矩阵运算，因此不会消耗算力，但这些未激活的参数需要占用显存（存储权重），这是 MoE 模型的显存瓶颈，非算力瓶颈，而是存储瓶颈。

3. 计算密度

计算密度决定了 "算力是否被浪费"，直接影响实际的算力成本（同样的 FLOPs，计算密度高的模型能完成更多有效任务）。

3.1 Decoder-only 架构：计算密度最高

• 优势：架构简洁，没有额外的跨模块计算（如 Encoder-Decoder 的跨注意力），也没有额外的门控网络消耗，所有算力都集中在"自注意力"和"前馈网络"的核心计算上。
• 场景优化：推理阶段的 KV 缓存进一步提升了计算密度，避免了重复计算注意力，减少了算力浪费。

3.2 Encoder-Decoder 架构：计算密度中等

• 劣势：跨注意力机制需要在 Encoder 和 Decoder 之间传递数据，存在一定的数据搬运开销，显存与算力核心之间的传输，这部分开销不产生有效计算，会降低计算密度。
• 补充：训练阶段，Encoder 和 Decoder 可以并行计算的部分较少，串行计算占比更高，也会导致算力利用率降低，进一步拉低计算密度。

3.3 MoE 架构：计算密度有优势但存在瓶颈

• 优势：稀疏激活让算力集中在有效专家模块上，避免了密集模型中"所有参数都参与计算"的冗余，在超大参数量任务中，计算密度远高于前两种密集架构。
• 瓶颈：算力节省的天花板
  • 门控网络开销：专家数量越多，门控网络的计算和数据搬运开销越大，会抵消部分稀疏激活的算力节省。
  • 专家负载不均衡：部分热门专家会被频繁激活，导致这些专家成为算力瓶颈，而部分冷门专家几乎不被激活，造成资源浪费。
  • 数据搬运开销：专家模块通常分布在不同的算力设备（如 GPU/TPU）上，输入数据需要被分配到对应的专家设备上，计算结果又需要被汇总，这个跨设备数据搬运的开销（通信成本）会大幅降低计算密度，这是 MoE 模型算力节省的最大瓶颈，尤其是分布式训练场景。

四、MoE 算力节省原理

MoE 的核心思想可以通俗理解为："一个公司有 100 个专家（专家模块），处理一个任务时，只需要找 2 个最擅长的专家来完成，不需要所有专家都参与，这样既节省了人力（算力），又能保证任务质量（模型能力）"。

1. 算力节省的核心原理

1.1 模块拆分：将密集模型的前馈网络（FFN）拆分为多个独立的专家模块

• 前馈网络是 Transformer 架构中算力消耗的第二大头，仅次于注意力机制
• MoE 只拆分前馈网络，注意力网络仍保持密集，保证上下文关联能力
• 每个专家模块都是一个独立的前馈网络，参数互不共享。

1.2 稀疏激活：通过门控网络选择少量专家参与计算

• 对于每个输入的 token（文本的最小单位，如一个字、一个词），门控网络会计算每个专家的匹配度；
• 然后选择 Top-k（通常 k=2）个专家来处理这个 token，其余专家不激活，不进行任何计算，也不更新参数。

1.3 结果汇总：将激活专家的输出结果加权求和，作为最终输出

• 门控网络同时会输出每个激活专家的权重，将专家的输出结果加权汇总后，传递到下一个网络层，这个汇总过程的算力消耗极低。

2. 算力节省的数学表达

假设：

• 密集模型前馈网络参数量为 P，算力消耗为 F。
• MoE 模型将前馈网络拆分为 E 个专家模块，每个专家参数量为 P/E（总参数量为 P，与密集模型一致）。
• 每个 token 选择 k 个专家参与计算，稀疏系数 s = k/E。

则 MoE 模型前馈网络的算力消耗为 F × s（注意力网络算力消耗与密集模型一致），当 E 很大（如 E=100），k 很小（如 k=2）时，s=0.02，前馈网络算力消耗仅为密集模型的 2%，整体算力消耗大幅降低。

如果要进一步提升模型能力，只需增加专家数量 E（总参数量增加），但稀疏系数 s 保持不变，算力消耗几乎不增加，这就是 MoE 模型"参数量与算力解耦"的核心优势。

3. MoE 算力节省的瓶颈

• **门控网络开销：**门控网络需要为每个token计算所有专家的匹配度，专家数量E越多，门控网络的算力消耗越高，当E达到一定规模时，门控网络的开销会抵消部分稀疏激活的收益。
• 专家负载不均衡：
  • 实际训练中，部分 token 会集中选择少数几个优秀的专家，导致这些专家被频繁激活成为热点专家，而其他专家几乎不被激活成为冷门专家。
  • 热点专家会成为算力瓶颈，所有分配到该专家的 token 都需要排队计算，而冷门专家的资源被闲置，导致整体算力利用率降低，无法达到理论上的稀疏收益。
• 通信成本瓶颈：
  • 分布式训练场景下，专家模块通常分布在不同的 GPU/TPU 上，一个 token 的数据需要被发送到对应的激活专家所在的设备上，计算完成后，结果又需要被发送回主设备进行汇总。
  • 这个跨设备的数据传输（通信）开销远大于计算开销，尤其是当专家数量多、设备数量多时，通信成本会成为 MoE 模型算力消耗的主要部分，大幅降低计算密度。
• **激活稀疏性的上限：**为了保证模型的稳定性和能力，k 不能太小（通常至少 k=1，实际常用 k=2），稀疏系数 s 不能无限降低，否则会导致模型的泛化能力下降（过度依赖少数专家），因此 MoE 模型的算力节省存在一个上限，无法实现零成本提升参数量。

五、长文本算力黑洞

长文本（如万字、十万字上下文）是大模型的重要场景，但也是公认的算力黑洞，其核心原因是注意力机制的平方级复杂度 和 KV 缓存的爆炸式增长。

1. 注意力机制的平方级算力复杂度

如前文所述，注意力机制的算力复杂度是 O (n² × d)，其中 n 是上下文长度，这个 "平方级" 是算力黑洞的核心来源。

通俗举例：

• 当 n=1024 时，注意力算力复杂度为 1024² × d = 1,048,576 × d。
• 当 n=16384（16 倍于1024）时，注意力算力复杂度为 16384² × d = 268,435,456 × d，是 n=1024 时的 256 倍（16²），而不是 16 倍。
• 当 n=100000 时，注意力算力复杂度会达到 10¹⁰ × d，这是一个天文数字，即使是顶级的 GPU/TPU 集群，也无法在合理时间内完成计算。

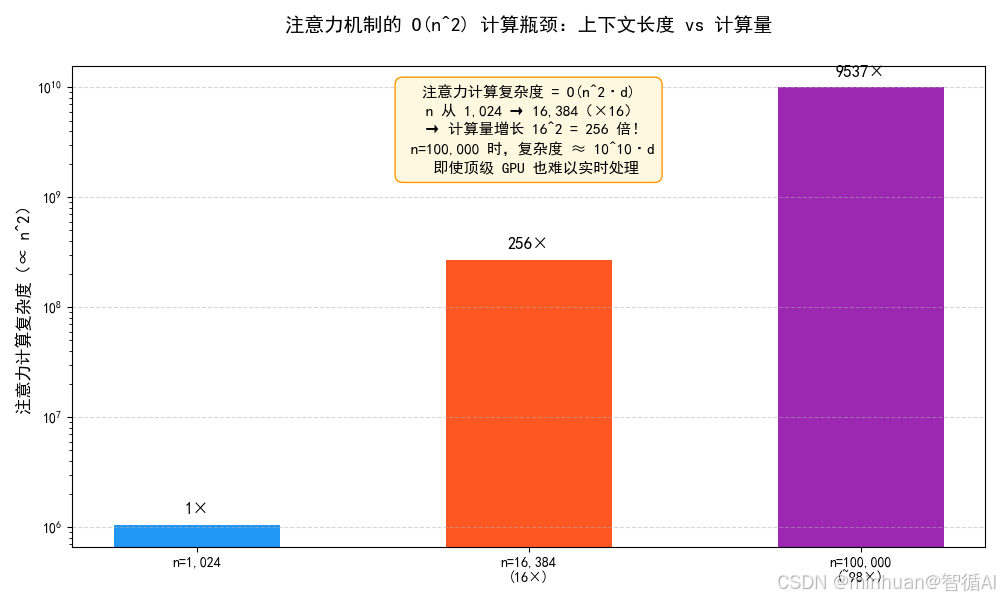
**技术细节：**长文本场景下，注意力机制的矩阵乘法会产生超大尺寸的矩阵（n×n），这个矩阵不仅计算量大，而且会占用大量显存存储矩阵中间结果，导致显存溢出，即使采用分布式存储，也会因为数据搬运开销过大而无法高效计算。

2. KV 缓存的爆炸式增长

KV 缓存是推理阶段优化注意力算力的核心手段，但在长文本场景下，它会从优化手段变成存储黑洞，间接推高算力成本。

• 1. KV 缓存的工作原理：
  • 推理阶段，模型生成第一个 token 时，会计算并缓存对应的 K 和 V 矩阵；
  • 生成第二个 token 时，只需计算新 token 的 Q 矩阵，与缓存的 K、V 矩阵进行注意力计算，无需重新计算前一个 token 的 K、V 矩阵；
  • 以此类推，后续每个 token 的生成，都只需计算新 token 的 Q 矩阵，与缓存的所有历史 K、V 矩阵进行计算。
• 2. KV 缓存的存储复杂度：O (n × d)（线性复杂度），虽然低于注意力机制的平方级复杂度，但长文本场景下，n 极大，存储消耗依然会爆炸式增长。
• 3. 通俗举例：
  • 假设模型隐藏层维度 d=4096，n=1024 时，KV 缓存的存储量约为 1024 × 4096 × 2（K 和 V）= 8,388,608 个参数，约 32MB（单精度浮点数）。
  • 当 n=16384 时，KV 缓存的存储量约为 16384 × 4096 × 2 = 134,217,728 个参数，约 512MB，是 n=1024 时的 16 倍。
  • 当 n=100000 时，KV 缓存的存储量约为 100000 × 4096 × 2 = 819,200,000 个参数，约 3.2GB，这还只是单个 token 的 KV 缓存，批量推理时，存储量会乘以批量大小，轻松占用几十上百 GB 的显存。

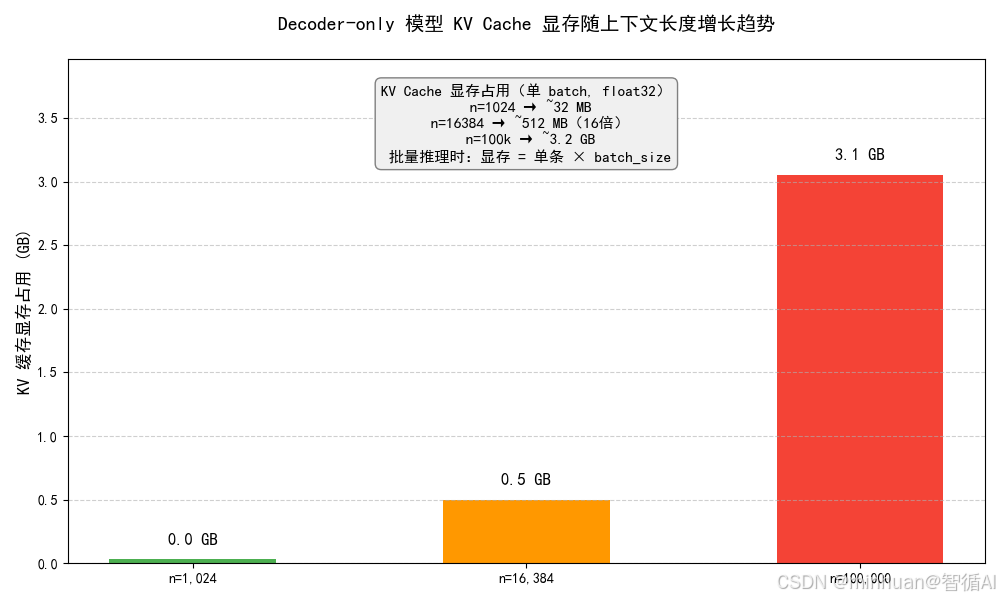
• 4. 间接推高算力成本：
  • 显存是稀缺资源，KV 缓存占用大量显存后，会导致模型无法进行大批量推理，只能降低批量大小；
  • 从而降低算力利用率（算力核心处于闲置状态），完成同样的推理任务需要更多的时间和更多的设备，间接推高了算力成本

3. 长文本算力黑洞的缓解手段

• 注意力机制优化：采用稀疏注意力，如 Longformer 的滑动窗口注意力、Performer 的核函数注意力，将算力复杂度从 O (n² × d) 降至 O (n × d) 或 O (n × log n × d)。
• KV 缓存优化：采用 KV 缓存压缩（如量化、剪枝）、KV 缓存丢弃（如只缓存最近的部分上下文），减少存储消耗。
• 模型架构优化：采用 Decoder-only 架构（推理友好，KV 缓存优化空间大），避免 Encoder-Decoder 架构的额外开销。

六、架构选型的算力成本决策

对于实际应用，选择哪种架构，核心是在"模型能力"和"算力成本"之间找到平衡，以下是针对不同场景的选型建议，结合算力消耗特点：

1. 优先选择 Decoder-only 架构的场景

• 核心场景：自然语言生成（对话机器人、文案创作、文本总结）、中小参数量模型（≤ 100B）、推理效率要求高的场景（如在线服务、移动端部署）。
• 选型理由：
  • 1. 算力消耗低，无跨注意力开销，计算密度高，算力利用率高。
  • 2. 推理阶段可通过 KV 缓存大幅优化，推理速度快，算力成本低。
  • 3. 架构简洁，工程实现难度低，容易进行分布式训练和推理优化。
• 典型案例：企业级对话机器人、在线文本生成工具、移动端大模型。

2. 优先选择 Encoder-Decoder 架构的场景

• 核心场景：序列到序列任务（机器翻译、多轮问答、文本摘要生成）、对文本理解能力要求高于生成能力的场景。
• 选型理由：
  • 1. 双向注意力机制（Encoder端）对文本的理解能力更强，适合翻译、问答等需要精准理解输入的任务。
  • 2. 分工明确，Encoder 负责理解，Decoder 负责生成，在复杂序列任务中，模型能力优于同等算力的 Decoder-only 架构。
• 选型提醒：需要承担更高的算力成本，尤其是训练阶段，适合有充足算力资源的团队。
• 典型案例：专业机器翻译系统、智能问答机器人（知识库问答）、文本摘要生成工具。

3. 优先选择 MoE 架构的场景

• 核心场景：超大参数量模型（≥ 100B）、对模型能力要求极高（如通用人工智能、复杂任务推理）、有大规模分布式算力集群（多 GPU/TPU）的场景。
• 选型理由：
  • 1. 可以在可控的算力成本下，大幅提升模型参数量，从而提升模型能力。
  • 2. 稀疏激活的算力效率高，在超大参数量场景下，算力成本远低于密集模型Decoder-only和Encoder-Decoder。
• 选型提醒：
  • 1. 工程实现难度高，需要解决专家负载不均衡、跨设备通信等问题。
  • 2. 显存消耗高，需要存储大量未激活的专家参数，需要充足的显存资源。
  • 3. 推理阶段的稀疏激活优化难度大，推理效率通常低于同等激活参数量的 Decoder-only 架构。
• 典型案例：通用大模型、复杂任务推理系统，如数学推理、代码生成。

七、示例解析

1. 注意力算力复杂度计算与对比

import numpy as np

def calculate_attention_flops(n1, n2, d, architecture):
    """
    计算三种架构的注意力机制算力复杂度（相对值，以FLOPs为单位）
    :param n1: 输入序列长度（Encoder输入/Decoder-only上下文长度）
    :param n2: 输出序列长度（Decoder输出，Decoder-only架构下n2=n1）
    :param d: 模型隐藏层维度
    :param architecture: 架构类型，可选["decoder_only", "encoder_decoder", "moe_decoder_only"]
    :return: 相对算力复杂度（FLOPs）
    """
    if architecture == "decoder_only":
        # Decoder-only：因果掩码自注意力，复杂度 O(n1² × d)（n2=n1）
        n = n1
        flops = n ** 2 * d
        return flops
    
    elif architecture == "encoder_decoder":
        # Encoder-Decoder：Encoder双向自注意力 + Decoder因果自注意力 + 跨注意力
        # Encoder: O(n1² × d)
        encoder_flops = n1 ** 2 * d
        # Decoder因果自注意力: O(n2² × d)
        decoder_self_flops = n2 ** 2 * d
        # 跨注意力: O(n1 × n2 × d)
        cross_flops = n1 * n2 * d
        # 总算力
        total_flops = encoder_flops + decoder_self_flops + cross_flops
        return total_flops
    
    elif architecture == "moe_decoder_only":
        # MoE-Decoder-only：稀疏激活，稀疏系数s=0.02（k=2，E=100）
        s = 0.02
        n = n1
        flops = s * (n ** 2 * d)
        return flops
    
    else:
        raise ValueError("不支持的架构类型，请选择正确的架构")

# 设定实验参数（初学者可修改参数观察结果）
d = 4096  # 模型隐藏层维度（常见值：768、4096、8192）
n1_list = [512, 1024, 2048, 4096, 8192]  # 输入序列长度/上下文长度
n2 = 1024  # 输出序列长度（Encoder-Decoder架构专用）

# 存储三种架构的算力结果
decoder_only_flops = []
encoder_decoder_flops = []
moe_decoder_only_flops = []

# 计算每种序列长度下的算力复杂度
for n1 in n1_list:
    do_flops = calculate_attention_flops(n1, n2, d, "decoder_only")
    ed_flops = calculate_attention_flops(n1, n2, d, "encoder_decoder")
    moe_do_flops = calculate_attention_flops(n1, n2, d, "moe_decoder_only")
    
    decoder_only_flops.append(do_flops)
    encoder_decoder_flops.append(ed_flops)
    moe_decoder_only_flops.append(moe_do_flops)

# 打印结果（格式化输出，更易读）
print("=" * 80)
print("三种架构注意力算力复杂度对比（相对值，隐藏层维度 d={}，输出序列长度 n2={}）".format(d, n2))
print("=" * 80)
print("{:<15} {:<20} {:<20} {:<20}".format("输入序列长度", "Decoder-only", "Encoder-Decoder", "MoE-Decoder-only"))
print("-" * 80)
for i, n1 in enumerate(n1_list):
    do_f = f"{decoder_only_flops[i]:.2e}"
    ed_f = f"{encoder_decoder_flops[i]:.2e}"
    moe_do_f = f"{moe_decoder_only_flops[i]:.2e}"
    print("{:<15} {:<20} {:<20} {:<20}".format(n1, do_f, ed_f, moe_do_f))

输出结果：

=====================================================================

三种架构注意力算力复杂度对比（相对值，隐藏层维度 d=4096，输出序列长度 n2=1024）

=====================================================================

输入序列长度 Decoder-only Encoder-Decoder MoE-Decoder-only

---

512 1.07e+09 7.52e+09 2.15e+07

1024 4.29e+09 1.29e+10 8.59e+07

2048 1.72e+10 3.01e+10 3.44e+08

4096 6.87e+10 9.02e+10 1.37e+09

8192 2.75e+11 3.14e+11 5.50e+09

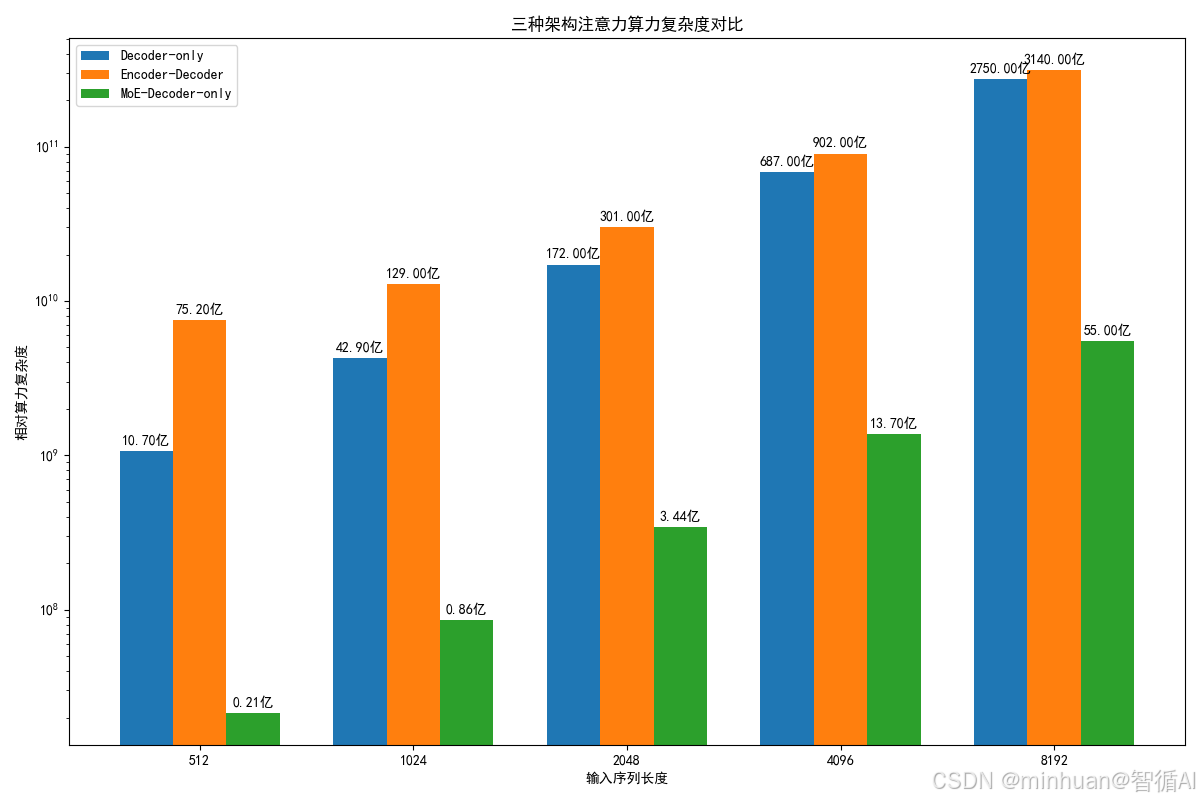
结果解析：

• 随着输入序列长度 n1 增加，三种架构的算力复杂度都快速增长，其中 Encoder-Decoder 增长最快，Decoder-only 次之，MoE-Decoder-only 最慢。
• MoE 架构的算力复杂度仅为 Decoder-only 架构的 2%，体现了稀疏激活的算力节省优势。
• 同等序列长度下，Encoder-Decoder 架构的算力复杂度约为 Decoder-only 架构的 2 倍左右，体现了双注意力机制的额外开销。

2. 算力对比可视化

import matplotlib.pyplot as plt
import numpy as np

# 沿用代码示例1的结果数据（如果已运行代码示例1，可直接使用；否则重新运行上述计算逻辑）
# 若未运行代码示例1，先执行以下初始化（保证代码独立运行）
d = 4096
n2 = 1024
n1_list = [512, 1024, 2048, 4096, 8192]
decoder_only_flops = []
encoder_decoder_flops = []
moe_decoder_only_flops = []

for n1 in n1_list:
    do_flops = n1 ** 2 * d
    encoder_flops = n1 ** 2 * d
    decoder_self_flops = n2 ** 2 * d
    cross_flops = n1 * n2 * d
    ed_flops = encoder_flops + decoder_self_flops + cross_flops
    moe_do_flops = 0.02 * (n1 ** 2 * d)
    
    decoder_only_flops.append(do_flops)
    encoder_decoder_flops.append(ed_flops)
    moe_decoder_only_flops.append(moe_do_flops)

# 设置中文显示（解决matplotlib中文乱码问题）
plt.rcParams["font.sans-serif"] = ["SimHei"]  # 用黑体显示中文
plt.rcParams["axes.unicode_minus"] = False  # 正常显示负号

# 创建画布
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))

# 子图1：三种架构算力复杂度对比（普通坐标）
ax1.plot(n1_list, decoder_only_flops, label="Decoder-only", marker="o", linewidth=2, color="#1f77b4")
ax1.plot(n1_list, encoder_decoder_flops, label="Encoder-Decoder", marker="s", linewidth=2, color="#ff7f0e")
ax1.plot(n1_list, moe_decoder_only_flops, label="MoE-Decoder-only", marker="^", linewidth=2, color="#2ca02c")

ax1.set_title("三种架构注意力算力复杂度对比（普通坐标）", fontsize=14)
ax1.set_xlabel("输入序列长度/上下文长度", fontsize=12)
ax1.set_ylabel("相对算力复杂度（FLOPs）", fontsize=12)
ax1.legend(fontsize=10)
ax1.grid(True, alpha=0.3)

# 子图2：三种架构算力复杂度对比（对数坐标，更清晰展示MoE的优势）
ax2.plot(n1_list, decoder_only_flops, label="Decoder-only", marker="o", linewidth=2, color="#1f77b4")
ax2.plot(n1_list, encoder_decoder_flops, label="Encoder-Decoder", marker="s", linewidth=2, color="#ff7f0e")
ax2.plot(n1_list, moe_decoder_only_flops, label="MoE-Decoder-only", marker="^", linewidth=2, color="#2ca02c")

ax2.set_title("三种架构注意力算力复杂度对比（对数坐标）", fontsize=14)
ax2.set_xlabel("输入序列长度/上下文长度", fontsize=12)
ax2.set_ylabel("相对算力复杂度（FLOPs，对数刻度）", fontsize=12)
ax2.set_yscale("log")  # 设置y轴为对数刻度
ax2.legend(fontsize=10)
ax2.grid(True, alpha=0.3)

# 调整布局，保存图片（保存到当前工作目录，格式为png）
plt.tight_layout()
plt.savefig("大模型架构算力对比图.png", dpi=300, bbox_inches="tight")
plt.show()

print("图片已保存为：大模型架构算力对比图.png")

结果图示：

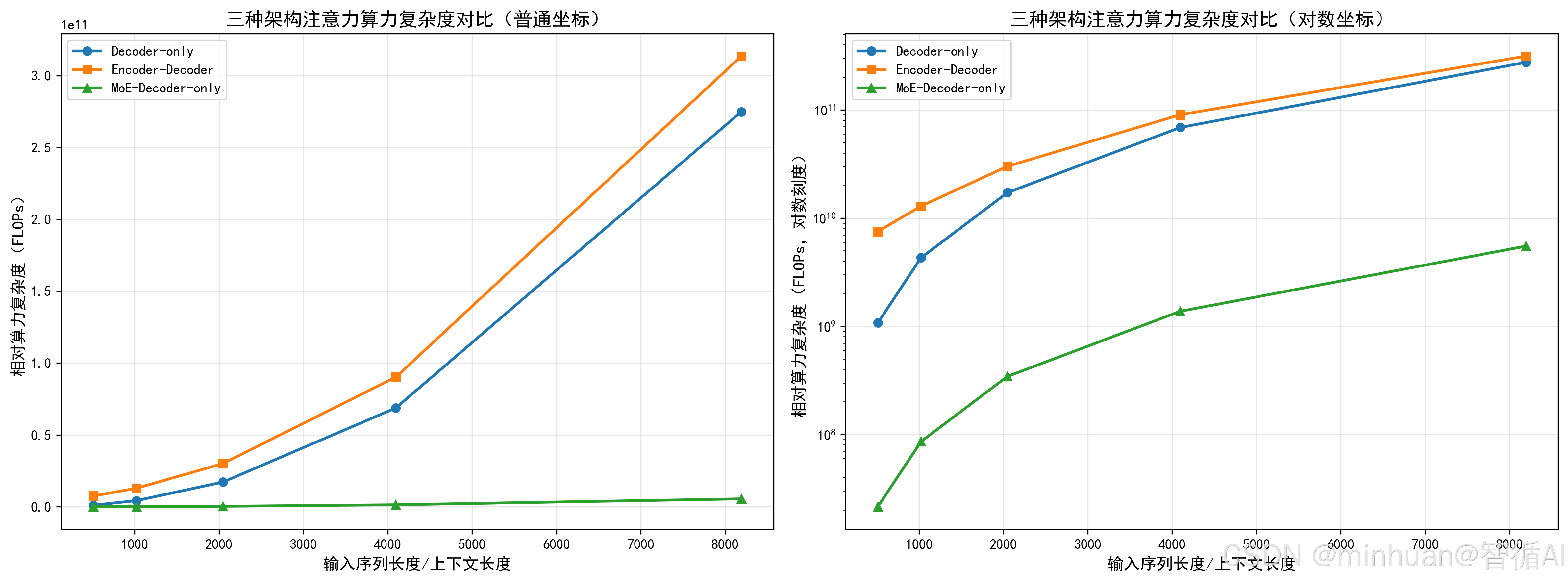
图例说明：

• 子图 1（普通坐标）：可以看到 Encoder-Decoder 和 Decoder-only 的算力曲线快速上升，MoE 的曲线几乎贴近 x 轴，体现了巨大的算力优势。
• 子图 2（对数坐标）：可以更清晰地看到三条曲线的增长趋势，MoE 的曲线增长最为平缓，Decoder-only 次之，Encoder-Decoder 最陡，直观展示了 "平方级增长" 和 "稀疏优化" 的差异。

3. MoE 专家负载不均衡模拟

import matplotlib.pyplot as plt
import numpy as np

def simulate_moe_expert_load(expert_num, token_num, top_k=2):
    """
    模拟MoE模型的专家负载不均衡情况
    :param expert_num: 专家数量
    :param token_num: token数量
    :param top_k: 每个token选择的专家数量
    :return: 每个专家的被激活次数（负载）
    """
    # 初始化专家负载
    expert_load = np.zeros(expert_num)
    
    # 为每个token选择top_k个专家（模拟热点专家，部分专家被选中概率更高）
    for _ in range(token_num):
        # 生成专家概率分布（前10%的专家是热点专家，被选中概率更高）
        expert_probs = np.ones(expert_num)
        hot_expert_num = int(expert_num * 0.1)
        expert_probs[:hot_expert_num] = 10  # 热点专家概率权重提升10倍
        
        # 归一化概率分布
        expert_probs = expert_probs / np.sum(expert_probs)
        
        # 选择top_k个专家
        selected_experts = np.random.choice(expert_num, size=top_k, replace=False, p=expert_probs)
        
        # 更新专家负载
        for expert in selected_experts:
            expert_load[expert] += 1
    
    return expert_load

# 设定实验参数
expert_num = 100  # 专家数量
token_num = 10000  # token数量
top_k = 2  # 每个token选择2个专家

# 模拟专家负载
expert_load = simulate_moe_expert_load(expert_num, token_num, top_k)

# 可视化专家负载
plt.rcParams["font.sans-serif"] = ["SimHei"]
plt.rcParams["axes.unicode_minus"] = False

fig, ax = plt.subplots(figsize=(12, 6))

# 绘制每个专家的负载
ax.bar(range(expert_num), expert_load, color="#1f77b4", alpha=0.7)

# 标注热点专家区域
ax.axvline(x=9, color="red", linestyle="--", label="热点专家与普通专家分界线（前10%）")

ax.set_title("MoE模型专家负载不均衡模拟（专家数量=100，Token数量=10000）", fontsize=14)
ax.set_xlabel("专家编号", fontsize=12)
ax.set_ylabel("被激活次数（负载）", fontsize=12)
ax.legend(fontsize=10)
ax.grid(True, alpha=0.3, axis="y")

# 保存图片
plt.tight_layout()
plt.savefig("MoE专家负载不均衡模拟图.png", dpi=300, bbox_inches="tight")
plt.show()

print("图片已保存为：MoE专家负载不均衡模拟图.png")
print("热点专家平均负载：{:.2f}".format(np.mean(expert_load[:10])))
print("普通专家平均负载：{:.2f}".format(np.mean(expert_load[10:])))

输出结果：

热点专家平均负载：1040.90

普通专家平均负载：106.57

结果图示：

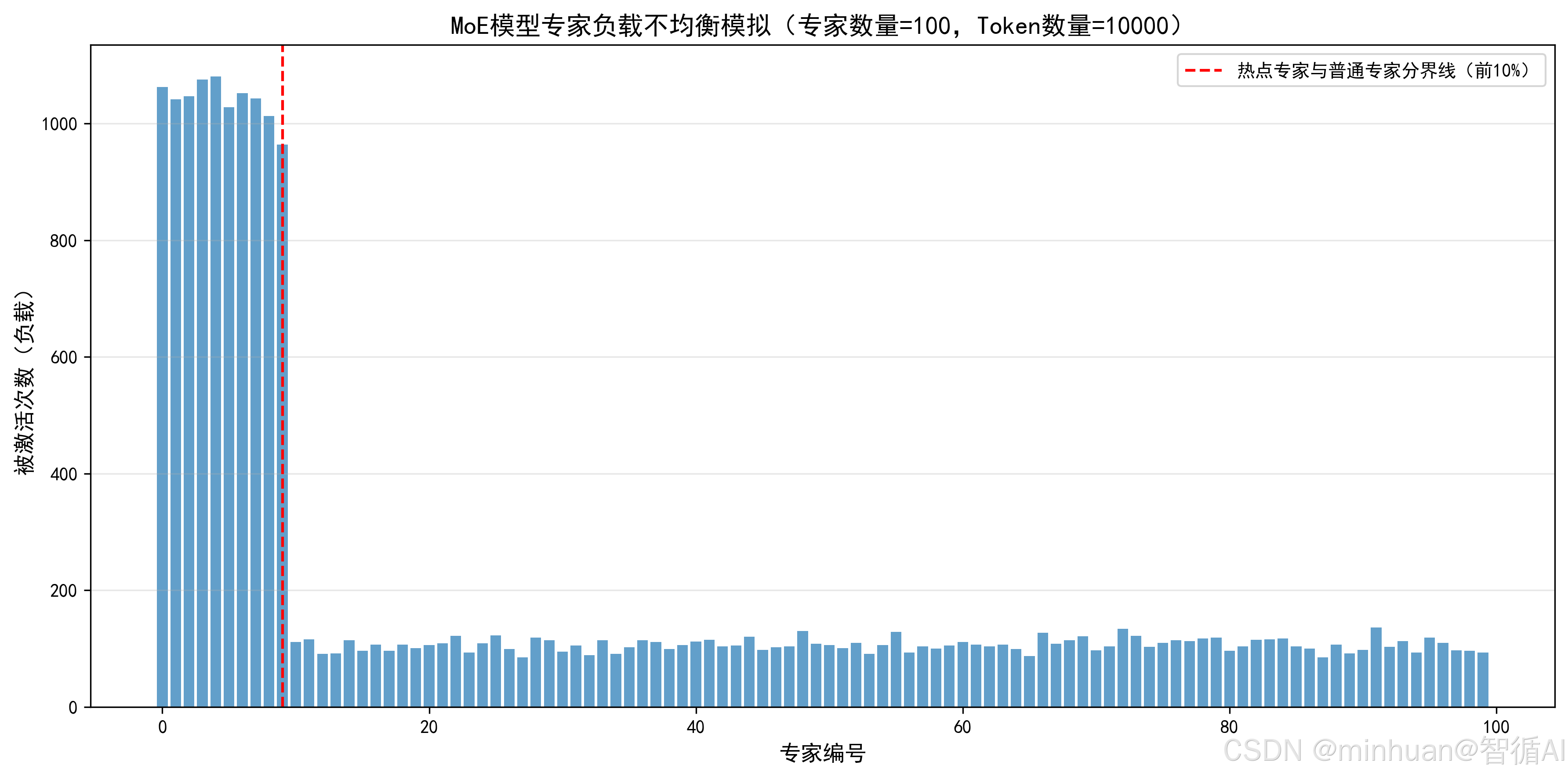
八、总结

理解三种架构的算力差异，对于我们学习和选型都具有重要意义：

• 指导模型选型：帮助开发者根据自身的算力资源、任务场景、性能要求，选择最合适的模型架构，避免 "算力过剩" 或 "算力不足"，降低开发成本和时间成本。
• 理解大模型发展趋势：大模型的发展始终围绕"提升能力"和"降低算力成本" 两个核心，Decoder-only 架构的流行、MoE 模型的兴起，都是算力优化的结果，理解算力差异可以帮助我们把握大模型的未来发展方向。
• 为模型优化提供思路：理解注意力机制、激活稀疏性、KV 缓存等核心算力消耗点，可以为模型优化提供明确的思路，如稀疏注意力、KV 缓存压缩、专家负载均衡优化等。
• 降低大模型的学习门槛：大模型的算力门槛是我们的主要障碍之一，理解算力差异可以帮助初学者选择合适的入门模型（如中小参数量的 Decoder-only 模型），避免因算力不足而无法开展实践。

三种大模型架构的算力核心差异主要体现在注意力机制、参数量与计算密度上，整体算力消耗从高到低依次为 Encoder-Decoder、Decoder-only、MoE 架构。MoE 依靠稀疏激活，仅让少量专家参与计算来大幅节省算力，但也面临门控网络开销、专家负载不均、跨设备通信成本高三大瓶颈。长文本场景则因注意力平方级复杂度与 KV 缓存暴涨形成算力黑洞，主要依靠优化注意力结构、压缩缓存来缓解。