排序算法
https://cloud.tencent.com/developer/article/2224857
https://developer.aliyun.com/article/1636639
1. 冒泡排序
1)从数组第一个开始,比较相邻两元素的大小,若后一个比前一个大,则两个数据交换,使得最大的元素排到数组末尾
2)在第二趟排序过程中,除了最后一个元素已经排列好,对其余元素也做上述操作
3)重复以上步骤,直到排序完成。
cpp
void BubbleSort(int a[])
{
int i=0;
int j=0;
int temp=0;
for(i=0;i<n-1;i++)
{
for(j=0;j<n-i-1;j++)
{
if(a[j] > a[j-1])
{
temp = a[j];
a[j] = a[j-1];
a[j-1] = a[j];
}
}
}
}2. 选择排序
1)从待排序数组中,选择一个最小的元素,放到数组第一个
2)从余下元素中,再选择一个最小的,放到第二个
3)重复以上步骤,直到数组排序完成
cpp
void selectSort(int a[])
{
int minIndex=0;
int i = 0, j = 0;
for(i=0; i<n-1; i++)
{
minIndex = i; //把当前位置假定为最小的位置,依次比较
for(j=i+1;i<n;j++)
{
if(a[j] < a[minIndex])
{
minIndex = j;
}
}
temp = a[i];
a[i] = a[minIndex];
a[minIndex] = temp;
}
}
// bubbleSort是最后一个元素放最大的,因此内循环j from 0 to n-i-1
// selectSort是第一个元素放最小的,因此内循环 j from i+1 to n3. 快速排序
4. 归并排序
5. 希尔排序
6. 堆排序
递归算法
递归:自己调用自己。
在解决问题时,把大问题化解成小问题,直到不能再分解,当小问题解决后,再逐步带入公式,最终能解决大问题
递归终止条件:在调用递归时,会越来越接近限制条件;当到达限制条件后,递归就会终止。
举例:阶乘 n!=n*(n-1)!
问题:当递归深度太深时,会发生栈溢出。如n=10000时,每次执行递归函数都会给函数分配内存,当递归完成时,内存才会被释放,因此会发生内存不足,栈溢出问题;同时,由于多次调用递归,也会发生效率低下问题。此时使用迭代解决。
迭代算法
迭代表示一种重复做的事情,比如本地DNS域名服务器在解析域名时,重复向根、顶级、权限域名查询。while for循环是一种迭代。
cpp
for (i=1;i<n;i++)
result*=i;【举例】斐波那契数列
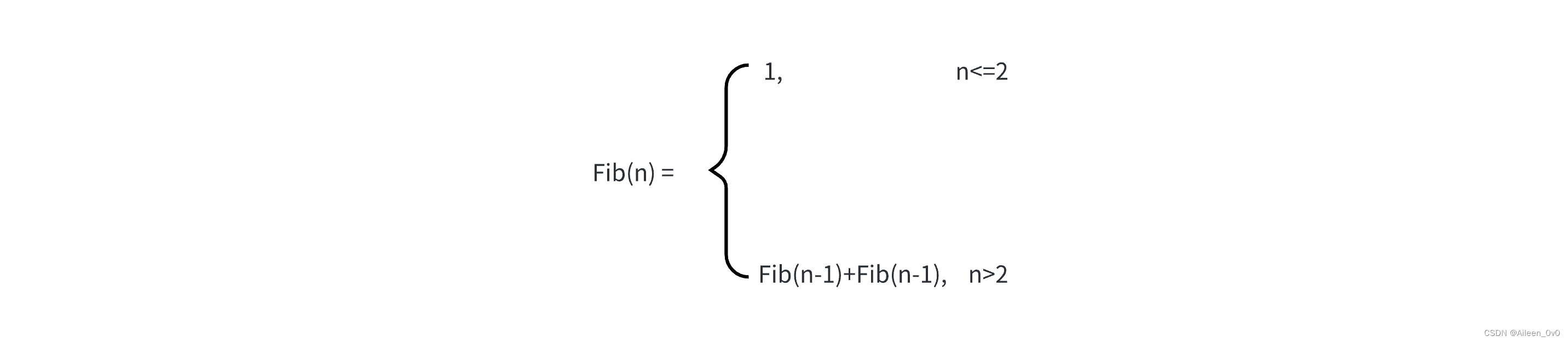
cpp
int Fab(n)
{
if(n <= 2) return 1;
return Fab(n-1) + Fab(n-2);
}
// 迭代
if(n=1) return 1;
a=1;
b=1;
for(i=1;i<n;i++)
{
result=a+b;
a=b;
b=result;
}
// 迭代
while(n>2)
{
result=a+b;
a=b;
b=result;
n--;
}图-最小生成树算法
从图的初始顶点出发,不形成回路,构造一棵最短带权路径长度的子树。工程中可以通过最小生成树算法,找到工程的最少花费。
1. Prim算法-背诵版/规范版
步骤:
(1)初始化一棵空树T,将初始顶点加入T
(2)重复以下步骤,直到图上所有顶点都加入T
①从T中某一个节点出发,在不形成回路的前提下,找到一条权值最小的边
②将这条边和边上的另一个顶点都加入T中
(3)即可得到最小生成子树T,返回T
伪代码:
cpp
void Prim(G,T) //G是图,T是树
Begin
T=空树
V={v} //V是树上节点的集合,v是图的初始顶点
while(U-V!=空) //U是图上顶点的集合,V是树上节点的集合
{
选择v∈V,u∈U,且(v,u)是权值最小的边
V=V U {u}
T=T U (v,u)
}
End2. Kruskal算法
步骤
(1)初始化时,将图上所有顶点都加入森林中,每个顶点算作一个连通分量
(2)重复以下步骤,直到森林中只有一棵树:
①从所有侯选边中选择一条权值最小的边,不能形成回路
②将这条边加入森林中
(3)最终森林中的这棵树T即为该图的最小生成子树
伪代码
cpp
void Kruskal(V,T) //V为图上顶点的集合,T为要生成的树
Begin
T=V //T为森林中节点集合,将图上所有顶点加入森林
nums = n //n为顶点个数,也是连通分量数量,每个顶点自成一个连通分量
while(nums>1)
{
选择一条权值最小的边(u,v),且u,v属于不同连通分量,不形成回路
T = T U (u,v) //将这条权值最小边加入森林
nums--;
}
End图-最短路径算法
可以找到花费时间最短的施工步骤。
1. Dijistra
步骤:找最近-定下来-借路过邻居
(1)初始化一个数组dist[],用于记录源点V到其他顶点的最短距离。初始化一个集合S,用于存储已经确定源点V已经确定最短距离的顶点集合。初始时刻dist[v]=0,其他值为∞,S={V}
(2)重复以下步骤,直到S中包含所有顶点
①从dist[]数组中,找到不在集合S中的且最小的值dist[u],并把相应的顶点U加入到集合S中
②计算顶点U相邻的且不在集合S中的顶点i的最短距离,dist[u]+(u,i),当dist[u]+(u,i)<dist[i]时,更新dist[i]=dist[u]+(u,i)
(3)最终获取到的dist[]数组中的值,即为源点V到其余各顶点的最短距离。
伪代码如下:
cpp
int[] Dijistra(V) //V是图的顶点集合
Begin
int dist[n]=∞;
dist[v]=0;//初始化dist数组,dist[v]=0,其余为∞,V是图的源点
S={V}; //初始化集合S,存储已经确定的源点到其余顶点的最短距离
while(S!=V)
{
从dist数组中选择一个顶点不在S中的且最小的值,dist[u]
S=S U {u}; //将顶点U加入集合S中
for(顶点U不在集合S中的相邻顶点i)
{
if(dist[i] > dist[u]+(u,i)
{
dist[i] = dist[u]+(u,i)
}
}
}
return dist[];
End