一、电机二次起步问题
1.1 第一次启动 (电机零速启动)
在电机零速启动时，电机的状态是：
(电角速度为 0)
此时我们的控制刚刚启动，给出的其内部的电流环 PI 和输出给定为：
之后积分器和 Uq 输出根据设计上升，电机正常启动，无问题。
1.2 第二次启动 (电机滑行中启动)
在电机滑行的状态时，电机的状态是：
根据 q 轴电压方程 (简化、稳态)：
将其变形得到：
此时因为我们的 ω 不为 0，导致 不为 0。但是我们控制器在刚刚启动是将 Uq 输出为 0，这就会导致，也就是此时的情况为：
这就会导致：
也就是转子已经在转了，但 q 轴电压不够，结果电机反推控制器。这种情况导致 q 轴电压瞬间为负，表现为电流环 PI 控制器被干扰，导致电流有冲击，反向力矩。
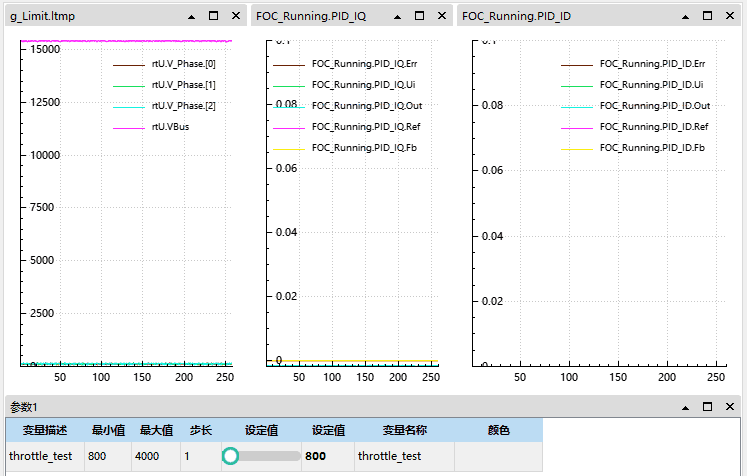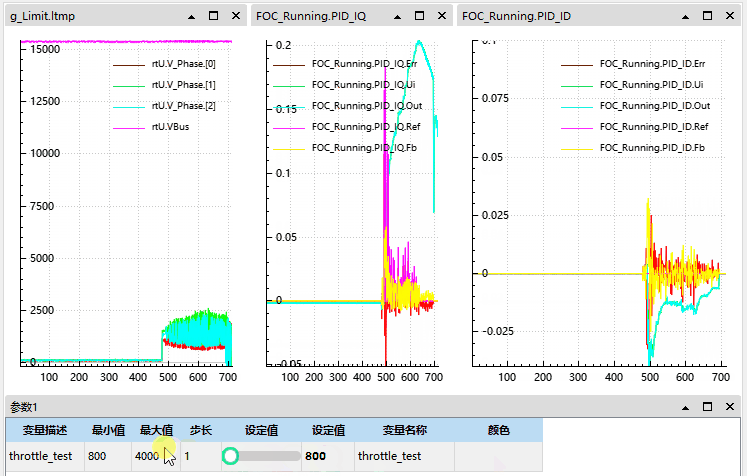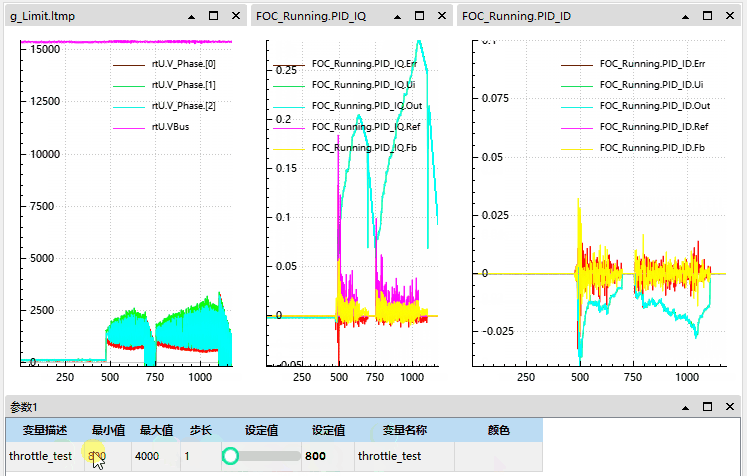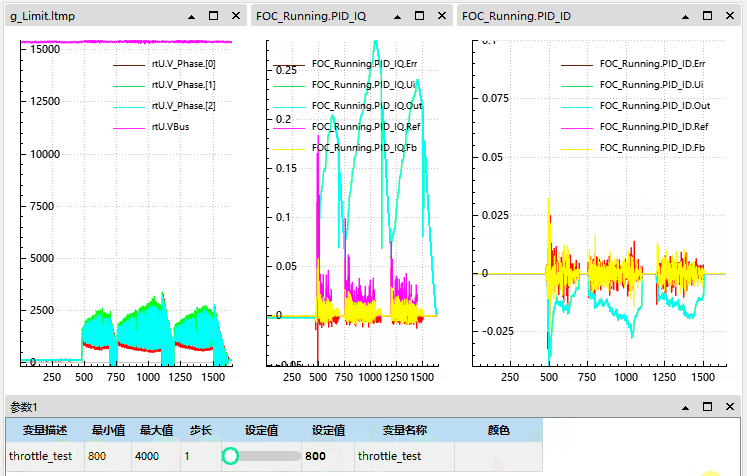
1.3 问题实际现象与总结
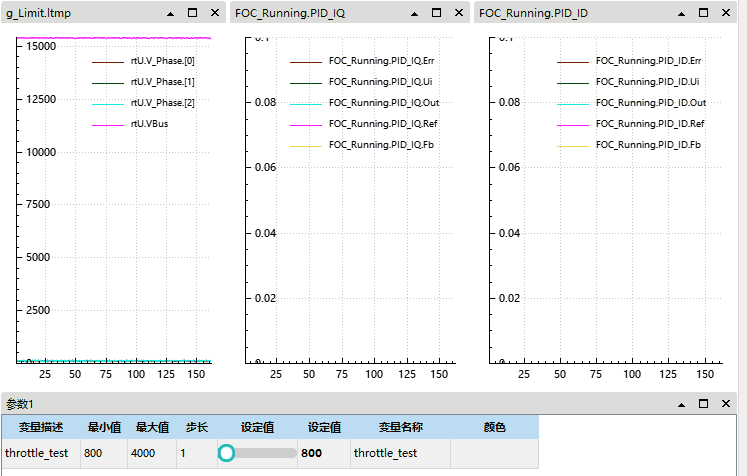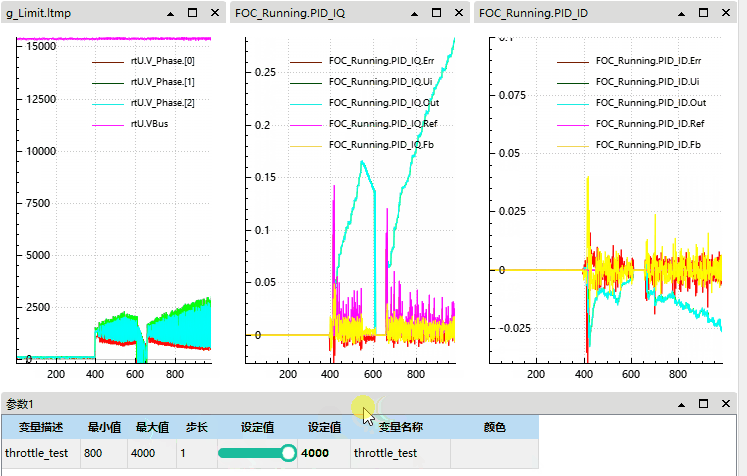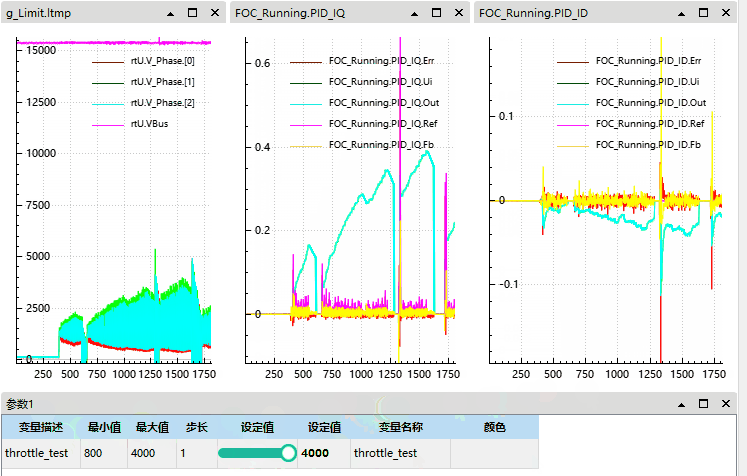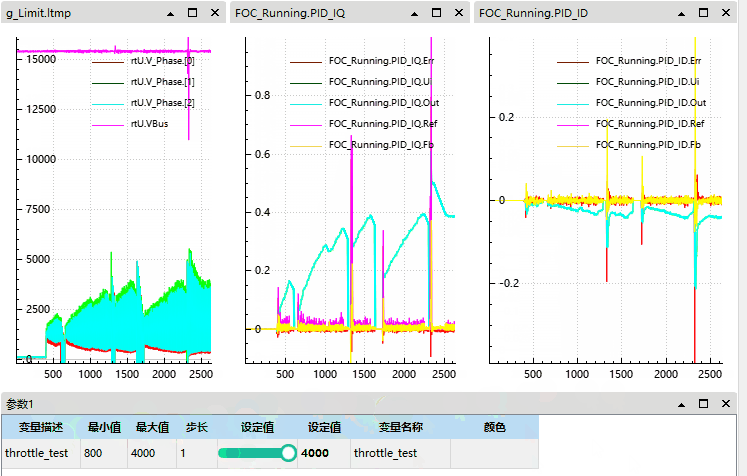
可见我们在电机有惯性 (有反电动势) 的情况启动后在电流和电压上均会出现尖峰：
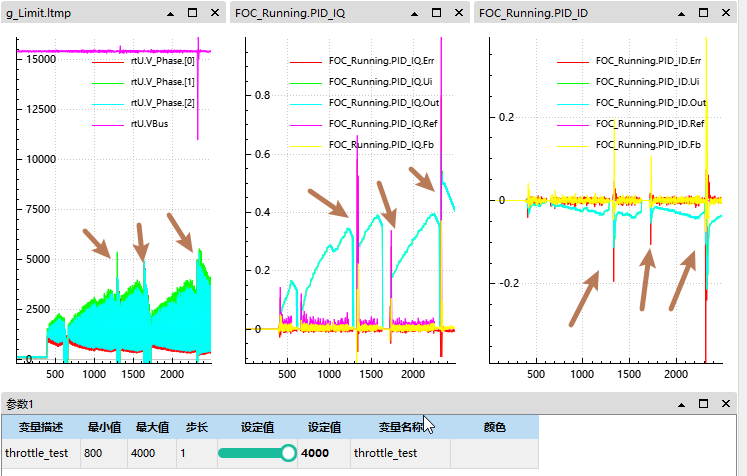
本质原因是电机已在转，反电动势已存在，而控制器接管瞬间 q 轴电压为 0 (或过小)，导致 q 轴电流瞬间为负，引发电流冲击和反向转矩。
二、解决办法
2.1 解决思路
二次起步的核心问题是接管瞬间 q 轴电压不足以抵消已存在的反电动势，导致 q 轴电流反向冲击。
解决办法是在进入闭环前，根据当前转速估算反电势，并将其作为 q 轴电压前馈或 PI 积分器初始值，使接管瞬间电压与电机状态匹配，从而实现无冲击切换。
也就是在二次起步进入闭环前：
为了实现这一步骤，我们在 Simulink 模型中输入母线电压、三项电压和转速 (转速只做判断方向使用)，最终我们输出的是近似的反电动势幅值，将其传递给我们的 q 轴 ki 的积分中，我们在二次启动电机时就用这个 ki 积分值，而不是 0。
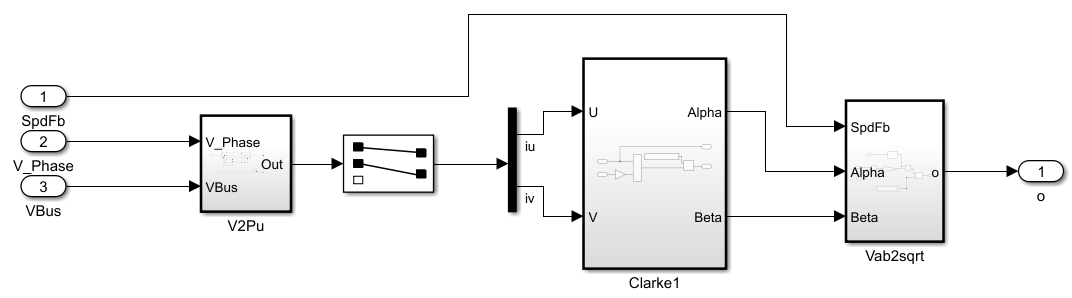
2.2 获取三项相电压
将我们获取的三项端电压取中点得到端电压，之后除以母线电压，得到 0~1 的标幺量：
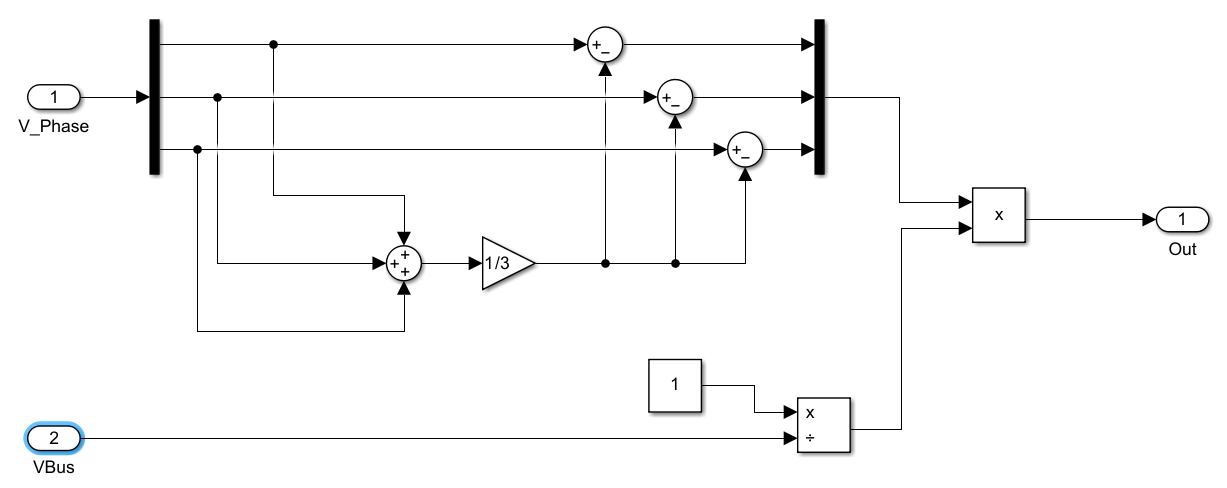
2.3 对电压进行 Clack 变换
对电压进行 Clack 变换得到 α、β 轴电压：
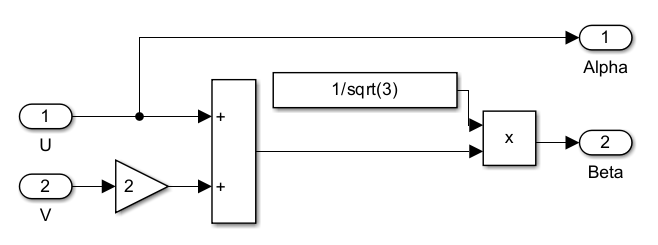
2.4 估算反电动势幅值
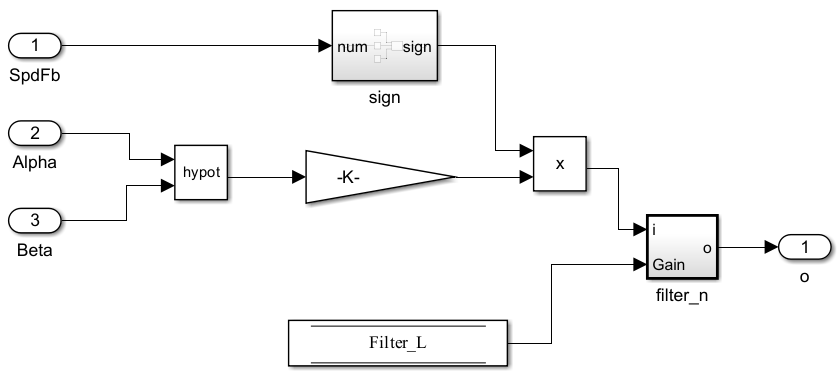
用 α、β 电压幅值估算反电动势幅值。
首先将 α、β 的电压值求 VS，也就是：
其中的 K 等于 ，这个常量将我们电压扩大到 SVPWM 能输出的尺度，再做低通滤波，作为一个稳定的反馈量输出。
Filter 做一个一阶低通滤波器使用，根据实际进行滤波效果设定即可。
2.5 全部的仿真框架
- ① 获取三项相电压
- ② 对电压进行 Clack 变换
- ③ 估算反电动势幅值
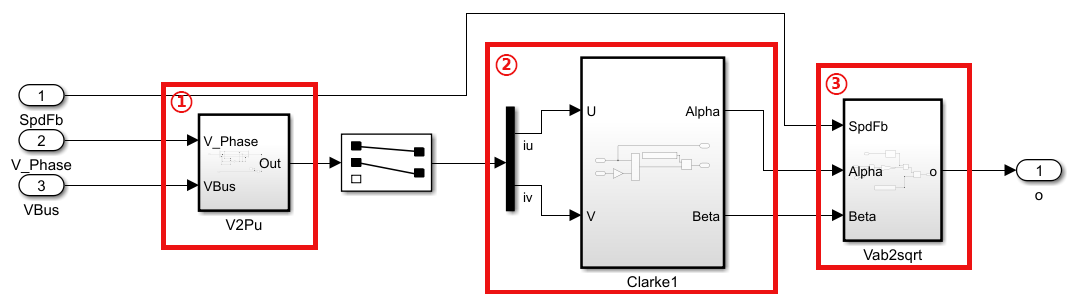
我们只需要在电机停止输出后 (iq、id均为 0) 调用这个模块，让其赋值给 iq 中 ki 的积分。
三、使用效果
可见，我们再二次启动时，不再有电压的尖峰了，电机也不会有异响。
