数据结构算法学习：LeetCode热题100-多维动态规划篇（不同路径、最小路径和、最长回文子串、最长公共子序列、编辑距离）

Gorgous—l2026-02-01 19:53

文章目录

  • 简介
  • [62. 不同路径](#62. 不同路径)
  • [64. 最小路径和](#64. 最小路径和)
  • [5. 最长回文子串](#5. 最长回文子串)
  • [1143. 最长公共子序列](#1143. 最长公共子序列)
  • [72. 编辑距离](#72. 编辑距离)
  • 个人学习总结

简介

本篇博客深入解析了 LeetCode 热题 100 中涉及多维动态规划的五个经典题目：不同路径、最小路径和、最长回文子串、最长公共子序列和编辑距离。内容涵盖网格路径与字符串处理两大类场景，通过详细拆解状态定义、状态转移方程及边界处理，结合具体的解题步骤与复杂度分析，帮助读者掌握利用二维 DP 解决复杂子问题的核心思路与技巧。

62. 不同路径

问题描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 "Start" ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 "Finish" ）。

问总共有多少条不同的路径？

示例：

标签提示： 数学、动态规划、组合数学

解题思想

这是一个经典的二维动态规划问题。由于机器人只能向下或向右移动，因此要到达网格的任意位置 (i,j)，其唯一的路径来源是它上方的位置 (i−1,j) 或者它左侧的位置 (i,j−1)。根据加法原理，到达 (i,j) 的路径总数等于到达这两个相邻位置的路径数之和。

解题步骤

  1. 状态定义：定义二维数组 dp，其中 dp[i][j] 表示从网格左上角 (0,0) 出发，到达位置 (i,j) 的不同路径数。
  2. 边界初始化：
    • 第一行的格子只能从左边到达，故对于所有 0≤j<n，有 dp[0][j]=1。
    • 第一列的格子只能从上边到达，故对于所有 0≤i<m，有 dp[i][0]=1。
  3. 状态转移：遍历网格的其余部分（从 i=1 到 m−1，j=1 到 n−1），对于每个位置 (i,j)，其路径数等于上方和左方路径数之和。状态转移方程为： d p [ i ] [ j ] = d p [ i − 1 ] [ j ] + d p [ i ] [ j − 1 ] dp[i][j]=dp[i−1][j]+dp[i][j−1] dp[i][j]=dp[i−1][j]+dp[i][j−1]
  4. 返回结果：最终返回右下角的值 dp[m-1][n-1]，即为到达终点的总路径数。

实现代码

java 复制代码 
class Solution {
    // 从左上往右下探索，非边界格，可以发现(i, j),的路径数取决于(i, j - 1)和(i - 1, j)的路径总和
    // 边界格（0行和0列）的路径数只能为1（一种走法，一直向下或者向右）
    public int uniquePaths(int m, int n) {
        int[][] dp = new int[m][n];
        for(int i = 0; i < m; i ++){
            dp[i][0] = 1;
        }
        for(int j = 0; j < n; j ++){
            dp[0][j] = 1;
        }
        for(int i = 1; i < m; i ++){
            for(int j = 1; j < n; j ++){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

复杂度分析

时间复杂度： O ( m × n ) O(m×n) O(m×n)

需要遍历整个二维数组 dp，外层循环执行 m 次，内层循环执行 n 次，总共执行 m ⋅ n m⋅n m⋅n 次计算。

空间复杂度： O ( m × n ) O(m×n) O(m×n)

使用了 m × n m×n m×n 大小的二维数组来存储状态值。

64. 最小路径和

问题描述

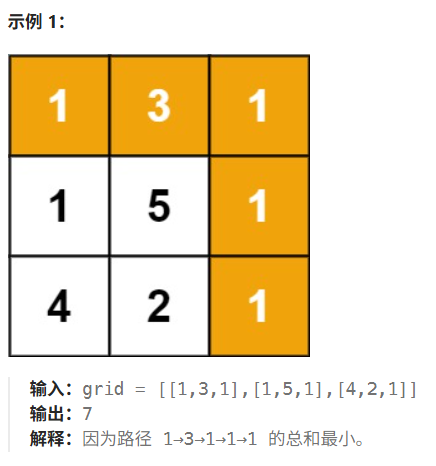
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

说明：每次只能向下或者向右移动一步。

示例：

标签提示： 数组、动态规划、矩阵

解题思想

采用动态规划解决。定义二维数组 dp，其中 dp[i][j] 表示从网格左上角 (0, 0) 出发，到达位置 (i, j) 的最小路径和。由于机器人只能向下或向右移动，因此要到达位置 (i, j)，路径必定经过其上方位置 (i-1, j) 或左侧位置 (i, j-1)。为了使路径和最小，取这两个位置中较小的路径和，再加上当前位置的数字 grid[i][j]。

解题步骤

  1. 状态定义：dp[i][j] 表示从起点 (0, 0) 到 (i, j) 的最小路径和。
  2. 状态初始化：
    • 起点：dp[0][0] = grid[0][0]。
    • 第一列（j=0）：只能从上方到达，路径和累加，即 dp[i][0]=dp[i−1][0]+grid[i][0]。
    • 第一行（i=0）：只能从左侧到达，路径和累加，即 dp[0][j]=dp[0][j−1]+grid[0][j]。
  3. 状态转移：遍历网格的其余部分（从 i=1 到 m-1，j=1 到 n-1），对于每个位置 (i, j)，状态转移方程为： d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) + g r i d [ i ] [ j ] dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j] dp[i][j]=min(dp[i−1][j],dp[i][j−1])+grid[i][j]
  4. 返回结果：返回右下角的值 dp[m-1][n-1]，即为最小路径和。

实现代码

java 复制代码 
class Solution {
    // 状态转移方程，当前位置（非边界）要么是向右走到，要么是向下走到
    // 然后是要求路径数最下
    public int minPathSum(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        dp[0][0] = grid[0][0];
        for(int i = 1; i < m; i ++){
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        for(int j = 1; j < n; j ++){
            dp[0][j] = dp[0][j - 1] + grid[0][j];
        }
        for(int i = 1; i < m; i ++){
            for(int j = 1; j < n; j ++){
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

复杂度分析

  • 时间复杂度： O ( m × n ) O(m×n) O(m×n)
    需要遍历整个二维数组 dp，其中 m 和 n 分别为网格的行数和列数。
  • 空间复杂度： O ( m × n ) O(m×n) O(m×n)
    使用了 m × n 大小的二维数组来存储所有状态值。

5. 最长回文子串

问题描述

给你一个字符串 s，找到 s 中最长的 回文 子串。

示例：

java 复制代码 
示例 1：
输入：s = "babad"
输出："bab"
解释："aba" 同样是符合题意的答案。

示例 2：
输入：s = "cbbd"
输出："bb"

标签提示： 双指针、字符串、动态规划

解题思想

利用动态规划解决。回文串具有"掐头去尾"后性质不变的特性：如果子串 s[i...j] 是回文串，那么去掉首尾后的子串 s[i+1...j−1] 也必然是回文串。基于此，定义状态 dp[i][j] 表示字符串从索引 i 到 j 的子串是否为回文串。通过判断首尾字符是否相等，以及去掉首尾后的子串状态，推导出当前状态。

解题步骤

  1. 状态定义：定义二维布尔数组 dp，dp[i][j] 为 true 表示子串 s[i...j] 是回文串。
  2. 边界初始化：
    • 单个字符必然是回文串，初始化 dp[i][i] = true。
    • 长度为 2 的子串若两字符相等，也是回文串（在后续逻辑中统一处理）。
  3. 状态转移：为了保证计算 dp[i][j] 时所需的子状态 dp[i+1][j-1] 已经被计算过，采用按子串长度 L 进行遍历的方式（从长度 2 到 n）。
    • 对于起始位置 i，结束位置 j = i + L - 1。
    • 若首尾字符不相等（s[i] != s[j]），则 dp[i][j] = false。
    • 若首尾字符相等（s[i]==s[j]）：
      • 当子串长度 L≤3 时（如 "aa" 或 "aba"），只需首尾相等即可确定为回文串，dp[i][j] = true。
      • 当子串长度 L>3 时，取决于内部子串的状态，状态转移方程为：dp[i][j]=dp[i+1][j−1]
  4. 记录结果：在计算过程中，记录出现过的最长回文子串的起始位置 start 和最大长度 maxL。
  5. 返回结果：根据 start 和 maxL 截取并返回最长回文子串。

实现代码

java 复制代码 
class Solution {
    // 回文串向内聚的子串也是回文串（掐头去尾），也就是(i,j)是回文串,那么(i+1,j-1)也是回文串
    // 抓住这一点去思考动态规划，那么使用dp[i][j]来表示(i,j)是否为回文串(布尔型)
    // 那么状态转移方程：当s[i] == s[j]时，dp[i][j] = dp[i+1][j-1];
    public String longestPalindrome(String s) {
        int n = s.length();
        // 单字母一定是回文串
        if(n < 2){
            return s;
        }
        // dp[i][j]存储(i,j)是否为回文串
        boolean[][] dp = new boolean[n][n];
        int maxL = 1;   // 记录最大回文串长度
        int start = 0;  // 记录最大回文串开始位置
        // 初始化dp，单个字母都是回文串
        for(int i = 0; i < n; i ++){
            dp[i][i] = true;
        }
        // 开始以回文串的长度L遍历，去更新数组
        for(int L = 2; L <= n; L ++){
            for(int i = 0; i <= n - L; i ++){
                // 子串的结束位置
                int j = i + L - 1;
                // 判断首尾是否相等
                if(s.charAt(i) != s.charAt(j)){
                    dp[i][j] = false;
                }else{
                    // 首尾相等的情况
                    // 1. 当L <= 3,一定是; 2. L > 3,则看其内部子串
                    if(L <= 3){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i + 1][j - 1];
                    }
                }
                if(dp[i][j] && L > maxL){
                    start = i;
                    maxL = L;
                }
            }           
        }
        return s.substring(start, start + maxL);
    }
}

复杂度分析

  • 时间复杂度： O ( n 2 ) O(n^2) O(n2)
    外层循环遍历子串长度 L 从 2 到 n，内层循环遍历起始位置 i。总的状态更新次数为 1 + 2 + ⋯ + ( n − 1 ) = n ( n − 1 ) 2 1+2+⋯+(n−1)=\frac{n(n-1)}{2} 1+2+⋯+(n−1)=2n(n−1) ，因此时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
  • 空间复杂度： O ( n 2 ) O(n^2) O(n2)
    使用了 n×n 的二维数组 dp 来存储所有子串的状态。

1143. 最长公共子序列

问题描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例：

java 复制代码 
示例 1：
输入：text1 = "abcde", text2 = "ace" 
输出：3  
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：
输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

标签提示： 字符串、动态规划

解题思想

采用二维动态规划解决。定义状态 dp[i][j] 表示字符串 text1 的前 i 个字符和字符串 text2 的前 j 个字符的最长公共子序列的长度。通过比较这两个字符串的末尾字符，利用子问题的解来构建原问题的解。为了避免处理数组越界和空字符串的情况，将 dp 数组的大小设为 (m+1) x (n+1)，其中第 0 行和第 0 列代表空字符串，其 LCS 长度显然为 0。

解题步骤

  1. 状态定义：定义二维数组 dp，dp[i][j] 表示 text1[0...i-1] 和 text2[0...j-1] 的最长公共子序列长度。
  2. 初始化：创建 dp 数组，大小为 (m+1) x (n+1)（m、n 分别为两字符串长度）。dp 数组初始化为 0，表示当其中一个字符串为空时，LCS 长度为 0。
  3. 状态转移：通过双重循环遍历 i 从 1 到 m，j 从 1 到 n：
    • 如果 text1 的第 i-1 个字符等于 text2 的第 j-1 个字符，说明该字符可以加入 LCS，长度加 1。状态转移方程为： d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] + 1 dp[i][j]=dp[i−1][j−1]+1 dp[i][j]=dp[i−1][j−1]+1
    • 如果不相等，说明该字符不能同时匹配，LCS 的长度取决于去掉 text1 的末尾字符或去掉 text2 的末尾字符后的较大值。状态转移方程为： d p [ i ] [ j ] = m a x ( d p [ i − 1 ] [ j ] , d p [ i ] [ j − 1 ] ) dp[i][j]=max(dp[i−1][j],dp[i][j−1]) dp[i][j]=max(dp[i−1][j],dp[i][j−1])
  4. 结果返回：遍历结束后，dp[m][n] 即存储了两个完整字符串的最长公共子序列长度，直接返回该值。

实现代码

java 复制代码 
class Solution {
    // 动态数组定义dp[i][j],定义为text1[0...i]与text2[0...j]的最长公共子序列
    // 边界dp[0][j]和dp[i][0]都为0，其中一个串为0
    // 可以把他视为一个二维表格，然后去辅助思考
    // 状态转移方程：当text1[i] == text2[j], 那么dp[i][j] = dp[i - 1][j - 1] + 1;
    // 状态转移方程：不等于时，dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
    public int longestCommonSubsequence(String text1, String text2) {
        int m = text1.length();
        int n = text2.length();
        if(m == 0 || n == 0){
            return 0;
        }
        // 多设置一行和一列（作为哨兵），防止越界问题，且便于计算
        int[][] dp = new int[m + 1][n + 1];
        // 这样就从1开始，注意字符串下标还是0开始的
        for(int i = 1; i <= m; i ++){
            for(int j = 1; j <= n; j ++){
                if(text1.charAt(i - 1) == text2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
                }
            }
        }
        return dp[m][n];    
    }
}

复杂度分析

时间复杂度： O ( m × n ) O(m×n) O(m×n)

其中 m 和 n 分别是 text1 和 text2 的长度。我们需要填充一个大小为 m×n 的二维表格，每个单元格的计算只需要常数时间。

空间复杂度： O ( m × n ) O(m×n) O(m×n)

使用了一个大小为 (m+1)×(n+1) 的二维数组 dp 来存储中间状态。

72. 编辑距离

问题描述

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

示例：

java 复制代码 
示例 1：
输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

标签提示： 字符串、动态规划

解题思想

本题属于经典的二维动态规划问题。目标是将单词 word1 转换成 word2，允许的操作包括插入、删除和替换字符。定义状态 dp[i][j] 表示 word1 的前 i 个字符（即 word1[0...i-1]）转换成 word2 的前 j 个字符（即 word2[0...j-1]）所使用的最少操作数。通过比较两个字符串的末尾字符，利用子问题的解来构建原问题的解。为了便于处理空字符串的情况（即其中一个字符串长度为0），dp 数组的大小设为 (m+1) x (n+1)，其中第 0 行和第 0 列代表空串。

解题步骤

  1. 状态定义：定义二维数组 dp，dp[i][j] 表示 word1 的前 i 个字符转换为 word2 的前 j 个字符的最小编辑距离。
  2. 边界初始化：
    • dp[i][0] = i：表示将 word1 的前 i 个字符全部删除，转化为空字符串，需要 i 次操作。
    • dp[0][j] = j：表示将空字符串通过插入 j 个字符，转化为 word2 的前 j 个字符，需要 j 次操作。
  3. 状态转移：通过双重循环遍历 i 从 1 到 m，j 从 1 到 n：
    • 如果 word1 的第 i-1 个字符等于 word2 的第 j-1 个字符，说明该位置无需操作，直接继承左上角的结果。状态转移方程为： d p [ i ] [ j ] = d p [ i − 1 ] [ j − 1 ] dp[i][j]=dp[i−1][j−1] dp[i][j]=dp[i−1][j−1]
    • 如果不相等，则需要进行操作（替换、插入或删除），取这三种情况的最小值加 1。状态转移方程为： d p [ i ] [ j ] = m i n ( d p [ i − 1 ] [ j − 1 ] , d p [ i ] [ j − 1 ] , d p [ i − 1 ] [ j ] ) + 1 dp[i][j]=min(dp[i−1][j−1], dp[i][j−1], dp[i−1][j])+1 dp[i][j]=min(dp[i−1][j−1],dp[i][j−1],dp[i−1][j])+1（其中，dp[i-1][j-1] 代表替换操作，dp[i][j-1] 代表插入操作，dp[i-1][j] 代表删除操作。）
  4. 返回结果：返回 dp[m][n]，即将整个 word1 转换为整个 word2 的最小编辑距离。

实现代码

java 复制代码 
class Solution {
    // 动态规划，dp[i][j]表示word1的前i个字符转化为word2的前j个字符需要多少步
    // 如果word1[i - 1] == word2[j - 1],那么dp[i][j] = dp[i-1][j-1];
    // 如果不等,dp[i][j] = min(dp[i - 1][j - 1],dp[i][j - 1],dp[i - 1][j]) + 1
    // 分别对应替换、插入和删除
    // 注意找对边界
    public int minDistance(String word1, String word2) {
        int m = word1.length();
        int n = word2.length();
        // 当其中一个为空串的时候，只需进行插入或删除操作即可
        if(m * n == 0){
            return m + n;
        }
        // 防止边界溢出
        int[][] dp = new int[m + 1][n + 1];
        // 初始化
        for(int i = 0; i <= m; i ++){
            dp[i][0] = i;   // 全部删除
        }
        for(int j = 0; j <= n; j ++){
            dp[0][j] = j;   // 全部插入
        }
        for(int i = 1; i <= m; i ++){
            for(int j = 1; j <= n; j ++){
                if(word1.charAt(i - 1) == word2.charAt(j - 1)){
                    dp[i][j] = dp[i - 1][j - 1];
                }else{
                    int rep = dp[i - 1][j - 1];     // 替换
                    int ins = dp[i][j - 1];     // 插入
                    int del = dp[i - 1][j];     // 删除
                    dp[i][j] = Math.min(Math.min(rep, ins), del) + 1;
                }
            }
        }
        return dp[m][n];
    }
}

复杂度分析

  • 时间复杂度： O ( m × n ) O(m×n) O(m×n)
    其中 m 和 n 分别是 word1 和 word2 的长度。我们需要填充一个 m×n 的二维表格，每个单元格的计算涉及常数次比较和赋值。
  • 空间复杂度： O ( m × n ) O(m×n) O(m×n)
    使用了一个大小为 (m+1)×(n+1) 的二维数组 dp 来存储所有状态。

个人学习总结

  1. 状态定义是核心：解决多维 DP 的关键在于明确 dp[i][j] 的物理含义（如到达某点的路径数、某子问题的最优解），正确的状态定义能直接简化后续转移方程的推导。
  2. 状态转移与逻辑：转移方程通常基于"最后一步"的选择。网格问题常依赖于上方或左方的状态；字符串问题（LCS、编辑距离）则多取决于两字符串末尾字符的匹配情况，需区分字符相等与不相等时的处理。
  3. 边界处理与遍历顺序：初始化边界（如 i=0 或 j=0 的情况）至关重要。遍历顺序需保证计算当前状态时，所需的子状态已经被计算过（如最长回文子串需按子串长度遍历）。
  4. 分类归纳：网格路径类问题通常涉及简单的累加或取极值；字符串类问题逻辑更复杂，常需考虑删除、插入、替换等操作对子问题的影响。
  5. 空间优化：虽然本文实现使用了二维数组（O(mn) 空间），但在实际应用中，这类问题往往可以利用滚动数组将空间复杂度优化至 O(n)。
相关推荐
熬夜造bug2 小时前
LeetCode Hot100 刷题路线（Python版）
算法·leetcode·职场和发展
2401_838472512 小时前
C++中的访问者模式
开发语言·c++·算法
老鼠只爱大米2 小时前
LeetCode经典算法面试题 #108：将有序数组转换为二叉搜索树（递归分治、迭代法等多种实现方案详解）
算法·leetcode·二叉树·二叉搜索树·平衡树·分治法
Hello_Embed2 小时前
libmodbus 移植 STM32（基础篇）
笔记·stm32·单片机·学习·modbus
独自破碎E3 小时前
【前缀和+哈希】LCR_011_连续数组
算法·哈希算法
一条大祥脚3 小时前
26.1.26 扫描线+数论|因子反演+子序列计数|树套树优化最短路
数据结构·算法
m0_561359673 小时前
基于C++的机器学习库开发
开发语言·c++·算法
星空露珠3 小时前
速算24点所有题库公式
开发语言·数据库·算法·游戏·lua
2401_832402753 小时前
C++中的类型擦除技术
开发语言·c++·算法
热门推荐
01GitHub 镜像站点02Clawdbot 中文汉化版 接入微信、飞书032026美赛A题智能手机电池续航时间预测的连续时间数学模型04OpenCode 入门教程：介绍 · 安装 · 配置第三方 API (如 Claude)05OpenClaw部署与配置教程：在Mac mini上接入国产大模型与飞书062025 年大语言模型发展回顾：关键突破、意外转折与 2026 年展望07Linux下V2Ray安装配置指南08UV安装并设置国内源09Claude Code + GLM4.7 避坑指南：解决 Unable to connect to Anthropic services10【Milvus】向量数据库pymilvus使用教程